基于電動伺服系統的轉向試驗臺阻力加載策略的研究?

陳國迎，何 磊，宗長富，顧興劍

前言

隨著虛擬仿真技術和電控伺服技術的快速發展，轉向系統硬件在環試驗臺已成為各汽車廠商和零部件供應商進行轉向系統產品開發的有效工具，以替代部分實車場地試驗達到縮短開發周期和降低開發成本的目的。轉向系統硬件在環試驗臺的核心在于高精度阻力加載系統，通過模擬實車轉向阻力矩可實現轉向系統參數測試、疲勞壽命測試和動態性能測試等功能[1-2]。

從現有文獻看，阻力加載主要采用電液伺服系統、直線電機和伺服電動缸等方案，這些系統在加載過程中受伺服系統內部摩擦、阻尼和慣量等非線性因素影響，閉環跟蹤壓力和電機電磁力矩與實際加載阻力并非簡單的比例關系，同時被測轉向系統的位移擾動產生的多余力也對阻力加載精度產生較大影響[3-5]。目前以英國ABD、德國IABG和德國IPG為代表的歐美車輛系統測試供應商已對阻力加載控制策略進行了深入研究，并開發出了高精度轉向系統性能測試臺架[6]。國內科研機構和高校主要側重于電控轉向系統控制算法的開發與驗證，大多數轉向試驗臺架的阻力模擬系統只適于簡單的加載，用于控制算法功能的驗證和對阻力模擬系統的加載控制策略則鮮有研究[6-10]。

針對這種現狀，本文中利用伺服電動缸進行轉向試驗臺的阻力模擬，著重對阻力模擬系統的加載控制策略進行研究，采用力閉環和前饋補償相結合的復合控制策略來提高電動伺服阻力模擬系統的加載精度，在此基礎上利用結構不變性原理抑制多余力的影響。

1 轉向試驗臺建模

圖1為建立的轉向試驗臺架結構，它包括電動伺服加載系統、S型拉壓力傳感器和齒輪齒條轉向器。電動伺服加載系統實時采集拉壓力傳感器信息，通過力閉環控制方法，對轉向系統進行精確阻力加載。轉向系統為小齒輪式電動助力轉向器，其輸出對阻力加載系統而言是典型的位移擾動，本文中采用位移閉環控制實現精確位移跟蹤。根據以上的臺架結構建立相應的數學模型。

圖1 轉向試驗臺架結構

1.1 電動伺服加載系統模型

電動伺服加載系統由永磁同步電動機、電機控制器和滾珠絲杠減速機構組成。由滾珠絲杠將電機的旋轉運動轉變為直線運動進行阻力加載。在永磁同步電動機的建模過程中，假設定子磁場磁路不飽和、無高次諧波和凸極效應，且定子磁場和轉子磁通呈理想正弦分布[11]。永磁同步電機的狀態方程可寫為

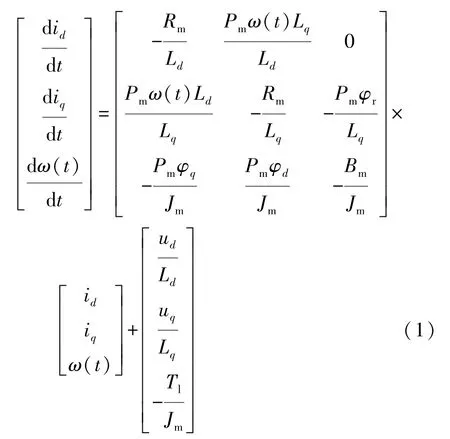
永磁同步電機在額定轉速以下通常采用id＝0的矢量控制策略。電機狀態方程經拉普拉斯變換后得到的傳遞函數為

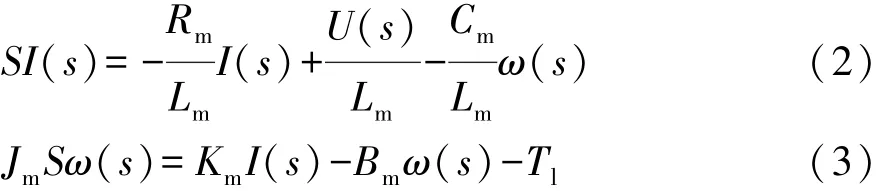
式中:ud和uq分別為d軸和q軸定子電壓；id和iq分別為d軸和q軸定子電流；φd和φq分別為d軸和q軸定子磁鏈；Rm為定子電阻；ω(t)為轉子角速度；Ld和Lq分別為d軸和q軸定子電感；φr為轉子磁鏈；Tm為電磁轉矩；Tl為負載轉矩；Jm為等效到電機軸的轉動慣量；Bm為阻尼系數；Km為力矩系數；Cm為反電動勢系數。

在同步電機的電流閉環跟蹤策略中，電流環控制器可認為是比例控制器。Kpm為電流控制增益，Kfm為電流反饋系數。電動伺服系統通過滾珠絲杠減速機構實現電機旋轉運動向直線運動的轉換。在滾珠絲杠的建模過程中，不考慮回程間隙的影響，同步電機與滾珠絲杠間視為剛性連接，將系統摩擦和慣量等效到電機軸上。

Ki為滾珠絲杠的傳動比，控制電壓信號為Vm，Kvm為控制電壓Vm與閉環跟蹤電流Im之間的比例系數。以控制電壓Vm為輸入、電動缸位移Sm為輸出的傳遞函數為

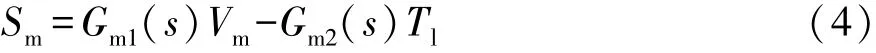
其中:

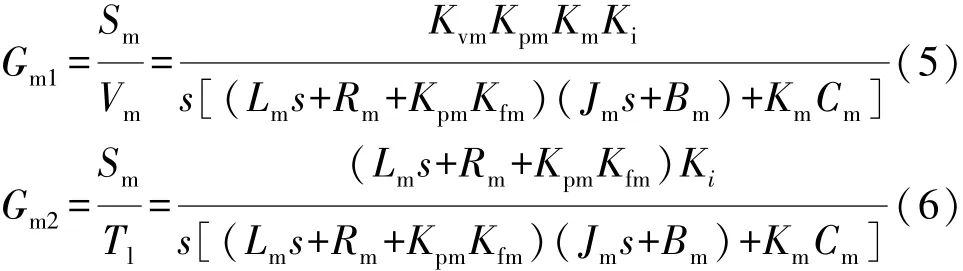
式中:Gm1(s)為加載電機力矩指令Vm到電動缸絲杠位移Sm的傳遞函數；Gm2(s)為加載系統的負載轉矩Tl到電動缸絲杠位移Sm的傳遞函數。

1.2 力傳感器模型

力傳感器進行電動伺服系統加載阻力的實時測量。在傳感器建模中忽略變形遲滯的影響，將電動缸位移與齒條位移差值作為傳感器彈性變形量引入，變形量大小與阻力值成線性關系。力傳感器模型方程為

式中:KT為傳感器剛度，N/mm；Sm為電動缸的位移，mm；Sr為齒條的位移，mm。

1.3 轉向系統模型

轉向系統建模過程中忽略齒輪齒條間隙，將轉向系統摩擦和阻尼等效到電機機械平衡方程中。轉向系統加裝光電碼盤實時采集小齒輪轉角，構成位移閉環控制系統。考慮轉向電機的位置環控制器KP(s)時，得到轉向系統的閉環結構框圖，如圖2所示。

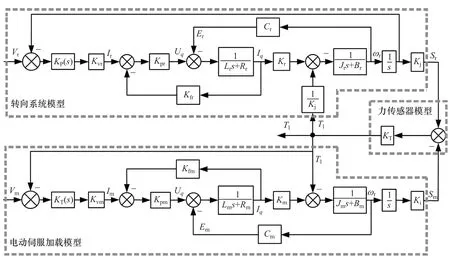
圖2 轉向試驗臺架模型

圖中:Vr為轉向電機角位移輸入的電壓信號；Kvr為輸入電壓Vin與Ir之間的比例系數；Kpr為電流控制增益；Kfr為電流反饋系數；Kr為力矩系數；Cr為電勢系數；Lr為電機電樞電感；Rr為電機電樞電阻；Jr為轉向系統等效到轉向電機輸出軸的轉動慣量；Br為轉向系統的阻尼系數；Kj為轉向系統的傳動比；Tl為加載系統對轉向系統的擾動力矩。

轉向系統的齒條位移輸出Sr的傳遞函數為

其中:

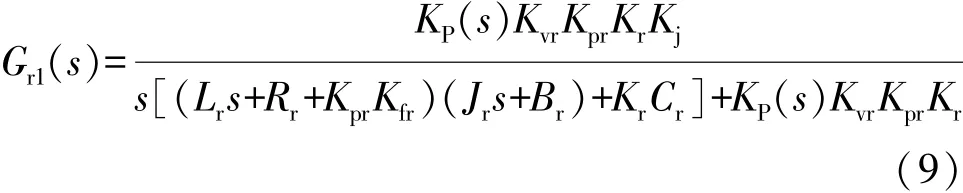
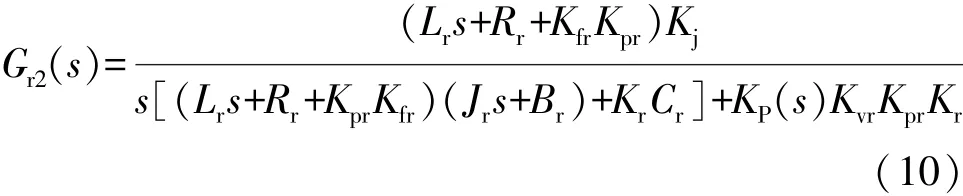
式中:Gr1(s)為轉向電機位置指令Ur(s)到齒條位移Sr的傳遞函數；Gr2(s)為電動加載系統對轉向系統的擾動Tl到齒條位移Sr的傳遞函數。

由于電動缸減速系統存在較大的摩擦和阻尼等非線性因素，電機軸輸出轉矩與電動缸最終輸出拉壓力并不是簡單的速比關系，故采用PID力閉環控制策略提高系統的跟隨能力和加載精度。將拉壓力信息引入電動伺服加載系統，構成實時力閉環控制系統。在以加載系統力矩控制指令Vm為輸入，轉向系統齒條位移Sr為擾動的情況下，得到最終閉環加載系統的傳遞函數為

其中:

式中:G1代表加載電機力矩指令Vr到電動缸輸出力矩Tl的傳遞函數；G2代表轉向系統齒條位移Sr到電動缸輸出力矩Tl的傳遞函數。

2 加載系統力閉環控制策略

加載系統采用PID力閉環控制策略來消除電動缸減速系統存在的摩擦、阻尼等非線性因素，提高系統的跟隨能力和加載精度。但這種控制方式降低了系統的阻尼，使加載系統處于臨界穩定或者不穩定狀態[12]。

利用表1的系統參數，對電動伺服加載系統的前向通道傳遞函數G1進行分析，系統由一個小時間常數慣性環節和2階振蕩環節串聯組成，且系統的阻尼很小。系統的傳遞函數[13]表達為

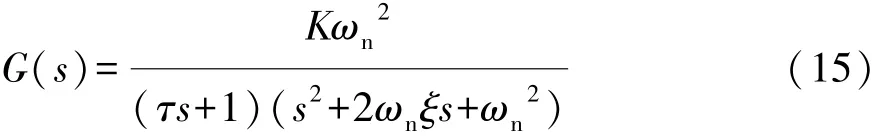
由于KTKiLm+RmBm>>KmCm，對式(12)進一步簡化可得

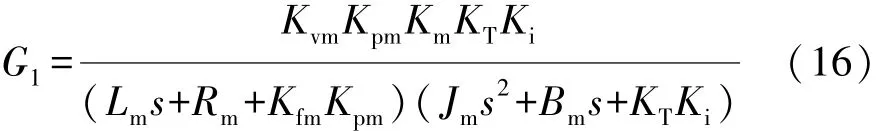
對比式(15)和式(16)可得

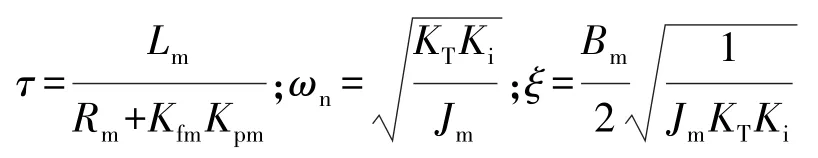
分析可知控制系統的電機參數和控制器參數決定系統負實根，系統的轉動慣量、阻尼系數和傳感器剛度決定了共軛復數的位置，決定系統的諧振頻率和系統的穩定裕度。

本文中采用零極點配置法，通過設計串聯校正環節增加控制系統的穩定性。增加的校正環節為

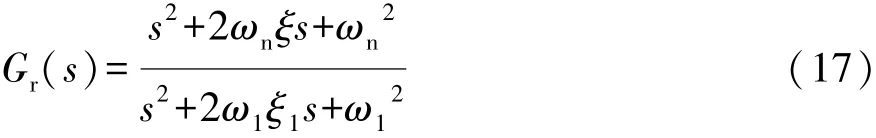
由式(17)可知，校正環節的分子與系統前向通道2階振蕩環節分母對消，校正后的系統的極點由s2+2ω1ξ1s+ω12＝0決定，其中 ξ1為系統期望阻尼系數，ω1為系統期望無阻尼自振頻率。由于系統的自然阻尼值很小，期望校正后系統的阻尼值更大，這里取ξ1＝1，ω1關系到系統的頻寬，取值越大系統頻帶寬度越大，但會引入過多的噪聲。考慮到轉向系統的轉動頻率一般在3Hz之內，所以ω1在保證系統快速性的前提下，取值盡量小，通過仿真最后確定ω1＝800rad/s，對校正后的系統進行分析。

圖3為校正后系統的根軌跡圖。由圖可見，校正后的系統通過兩個零點與未校正的系統的兩個靠近虛軸的共軛極點發生對消，同時將新的極點進行重新配置，新的極點距離虛軸有一定的距離。相比原有系統，校正后系統的增益大幅增加，臨界增益為5.2左右，這既保證系統有好的動態響應能力，同時也提高了系統的穩定裕度。

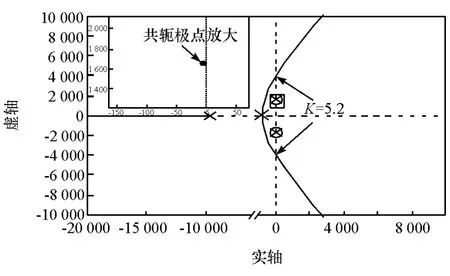
圖3 校正后系統根軌跡圖

圖4 為系統校正前后的伯德圖對比。由圖可見:系統未校正之前是不穩定的，穩定裕度和幅值裕度均為負值；校正之后系統的幅值裕度為 Gm＝14.6dB，相角裕度為 Pm＝40.6°；在 0～10Hz的頻率范圍內校正前后系統的幅值相差12.63dB，幅值裕度差值可通過調節力矩控制器增益來校正；相角差在8°范圍內，相角裕度差值可通過控制器參數改善。

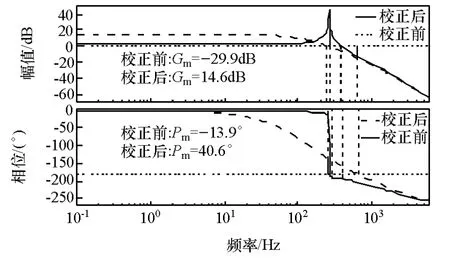
圖4 校正前后系統伯德圖對比

3 加載系統多余力的抑制

應用于轉向試驗臺的電動伺服缸是典型的被動式加載系統，在進行力加載的同時需要跟隨轉向齒條往復運動，在這個過程中會因轉向系統的位移擾動而產生多余力[14-16]。

圖5為多余力通道傳遞函數G2的頻域特性曲線。由圖可見:在中低頻段，微分環節起主導作用，相位超前90°以上，振幅隨輸入頻率升高而增大；在高頻段，多余力會由于系統的衰減作用在幅值上得到抑制；轉向系統通常的工作頻率在3Hz之內，因此多余力的存在會對控制系統的加載精度造成較大的影響。

圖5 多余力頻率特性曲線

針對加載系統存在的多余力問題，采用結構不變性原理結合速度前饋控制方法進行多余力的抑制。結構不變性原理是利用補償通道針對負載干擾提前施加控制余量，使干擾對系統的作用正、反相消，達到抑制多余力的效果[14]。圖6為多余力抑制算法框圖。

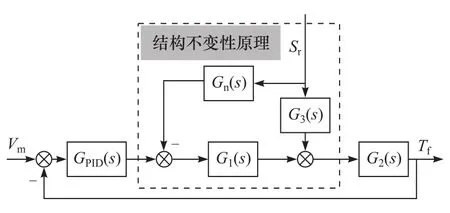
圖6 結構不變性原理框圖

多余力抑制補償通道的傳遞函數為

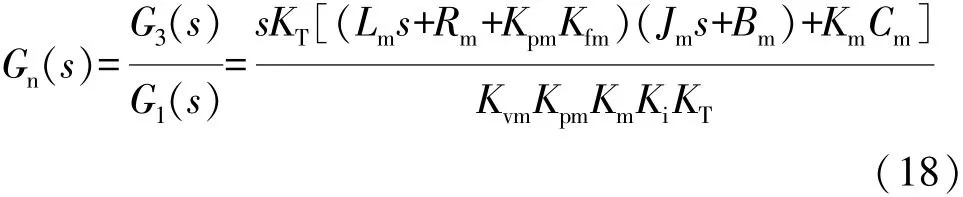
Gn(s)傳遞函數的分子冪次高于分母，為物理不可實現系統。本文中采用極點配置方式在傳遞函數中串聯3階慣性環節1/(T1s+1)3以增加分母的階次。時間常數T1的選取與多余力的抑制程度密切相關。時間常數越小，擾動產生的多余力的抑制效果越好，但同時帶來多余力的高頻振蕩。時間常數越大，系統的延遲越大，反而不利于降低多余力幅值。本文中根據試驗確定時間常數T1＝0.005。

為了消除3階慣性環節帶來的系統滯后，將速度前饋補償環節引入多余力的抑制控制中。速度信號由位置信號Sr微分求取，微分的過程同時引入了噪聲，因此需要進行濾波處理。速度前饋補償的傳遞函數為

式中kv為低通濾波器增益。濾波器引入過濾信號的噪聲，同時也會使信號的幅值衰減，調整濾波器增益可彌補幅值衰減值。

4 仿真分析

以第2節建立的轉向試驗臺模型為基礎，分別進行力閉環控制策略和多余力抑制策略的仿真驗證。驗證中采用的部分加載系統參數如表1所示。

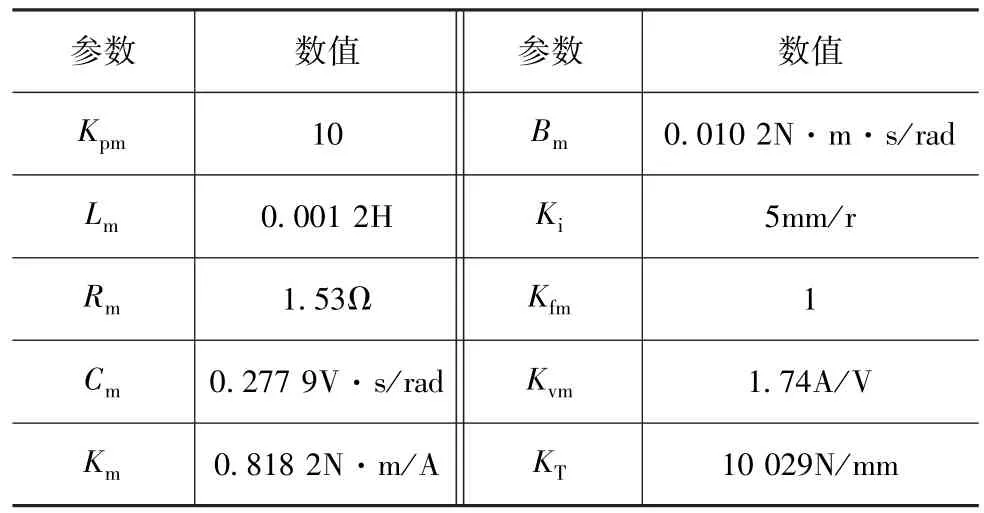
表1 加載系統參數列表

4.1 靜態加載情況下力閉環控制策略仿真

利用建立的轉向試驗臺架模型對力閉環控制策略進行仿真分析。為了避免轉向系統運動中產生的多余力對分析結果造成影響，位移值設定為零。

圖7為階躍輸入下力閉環仿真結果。由圖可見，系統的上升時間為tr＝0.012s，系統的調節時間為ts＝0.09s，系統的超調量為σ＝4.2%，穩態誤差很小，為ess＝0.01%，從階躍響應參數可見，系統具有很好的動態性能和穩定性能，校正后的系統能滿足加載系統的性能要求。

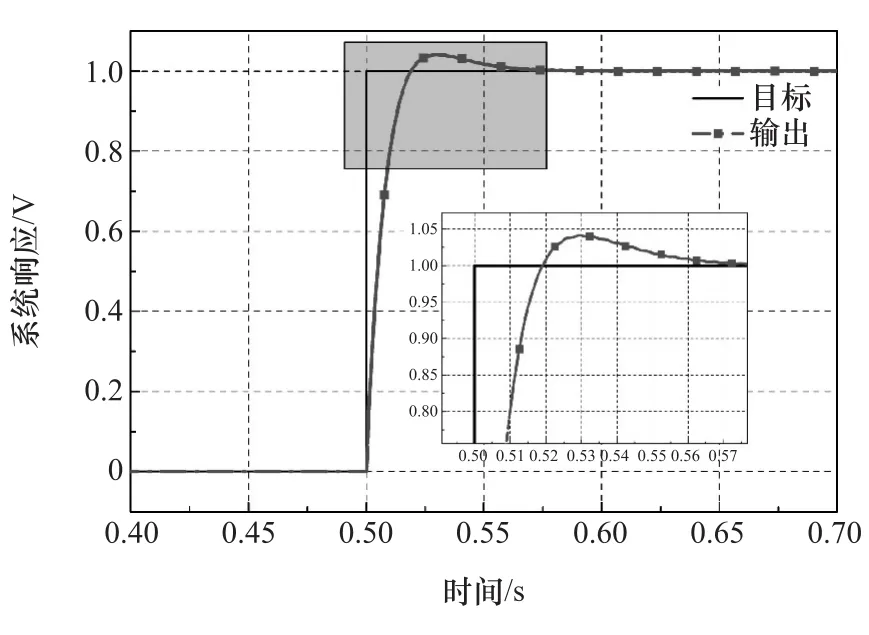
圖7 階躍輸入下力閉環仿真結果

圖8 為正弦輸入下的力閉環仿真結果，正弦輸入的幅值為3V，頻率為1Hz。由圖可見，輸出幅值衰減為 Gm1＝-0.02dB，輸出相位滯后為 Pm1＝0.36°。

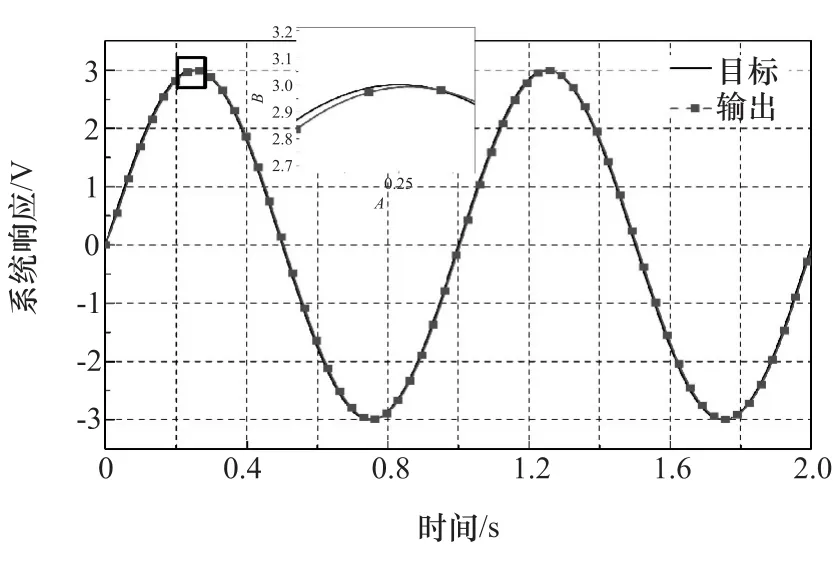
圖8 1Hz正弦輸入下力閉環仿真結果

4.2 轉向系統位移擾動下多余力抑制仿真

將Carsim車輛模型中車輪所受阻力力矩折算為加載電機的控制電壓信號，轉向盤轉角折算為齒條位移擾動，進行多余力抑制仿真。圖9為多余力抑制的效果曲線。由圖可見，基于結構不變性原理和速度補償后的多余力降低了53.3%。

5 臺架試驗驗證

結合仿真分析的結果，本文中利用實時仿真平臺dSPACE1103進行電動伺服加載系統力閉環控制策略和多余力抑制策略的臺架驗證試驗。

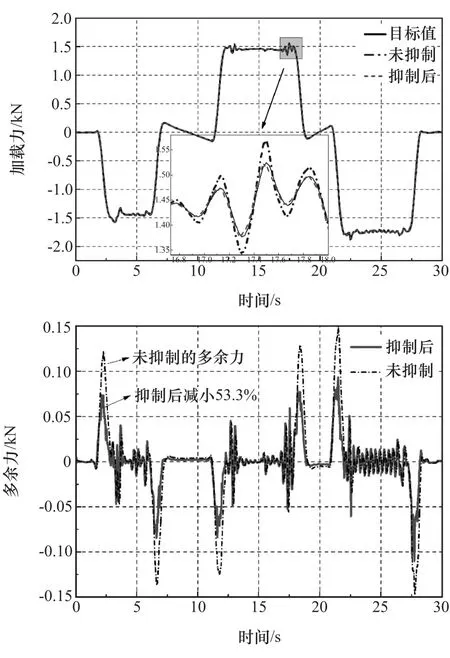
圖9 Carsim轉向輸入下多余力抑制效果

5.1 力閉環控制策略試驗驗證

為消除多余力對試驗結果的影響，試驗驗證中拉壓力傳感器的齒條端替換為L型支板固定。臺架結構如圖10所示。圖11為目標設定值為1 000N時，系統未加校正環節進行力矩閉環控制的試驗結果。此時，系統發生振蕩處于不可控狀態，振蕩峰值達到7 800N，對機械系統和傳感器的沖擊很大。

圖10 力閉環控制策略驗證臺架實物

在對力閉環控制系統進行串聯校正環節后，重新測試系統的穩定性和動態響應能力。圖12為目標加載力為1 000N時的階躍響應結果。為降低機械間隙對控制效果的影響，試驗初始時施加200N的預緊力。由圖可見，系統的上升時間tr＝0.052s，系統的調節時間ts＝0.16s，系統的超調量為σ＝2.9%，穩態誤差為ess＝0.18%。

圖11 未加校正環節的力矩閉環控制效果

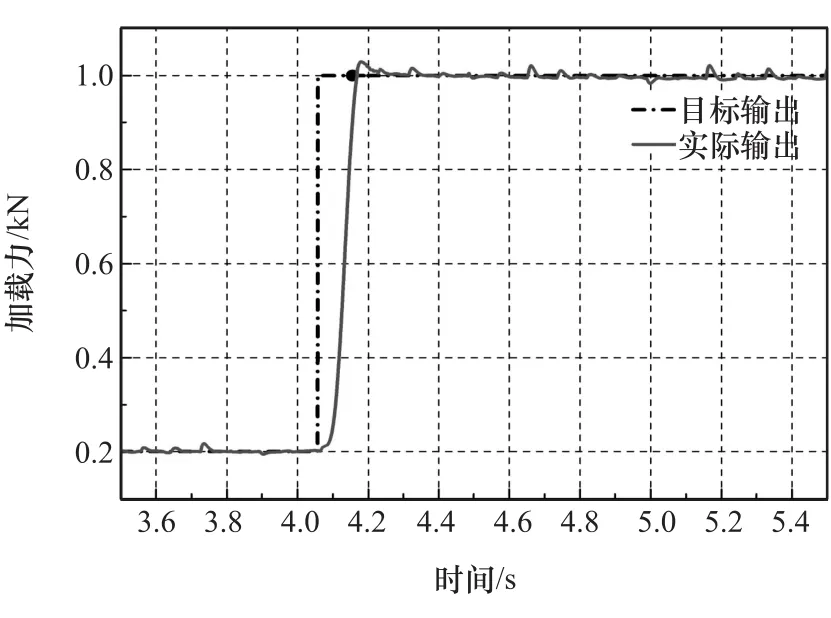
圖12 階躍輸入下力閉環控制效果

圖13 為加載力跟隨Carsim車輛模型齒條推力的響應曲線。由圖可見，加載力能較好地跟隨目標值，穩態誤差控制在20N的范圍內。

圖13 Carsim齒條推力輸入下力閉環控制效果

5.2 多余力抑制控制的試驗驗證

采用圖1的臺架進行多余力抑制的試驗驗證。齒條式轉向系統對加載系統的位移擾動頻率為0.5Hz、幅值為10mm，如圖14(a)所示。目標加載力設定為0。圖14(b)為擾動狀態下加載系統施加多余力抑制和未施加多余力抑制的結果對比曲線。由圖可見，未抑制的多余力為1 109.7N，抑制后的多余力為398.9N，抑制效果達到64%。圖14(b)中虛框區域內為控制參數切換區，過程中有較大的加載力沖擊，這部分不予考慮。

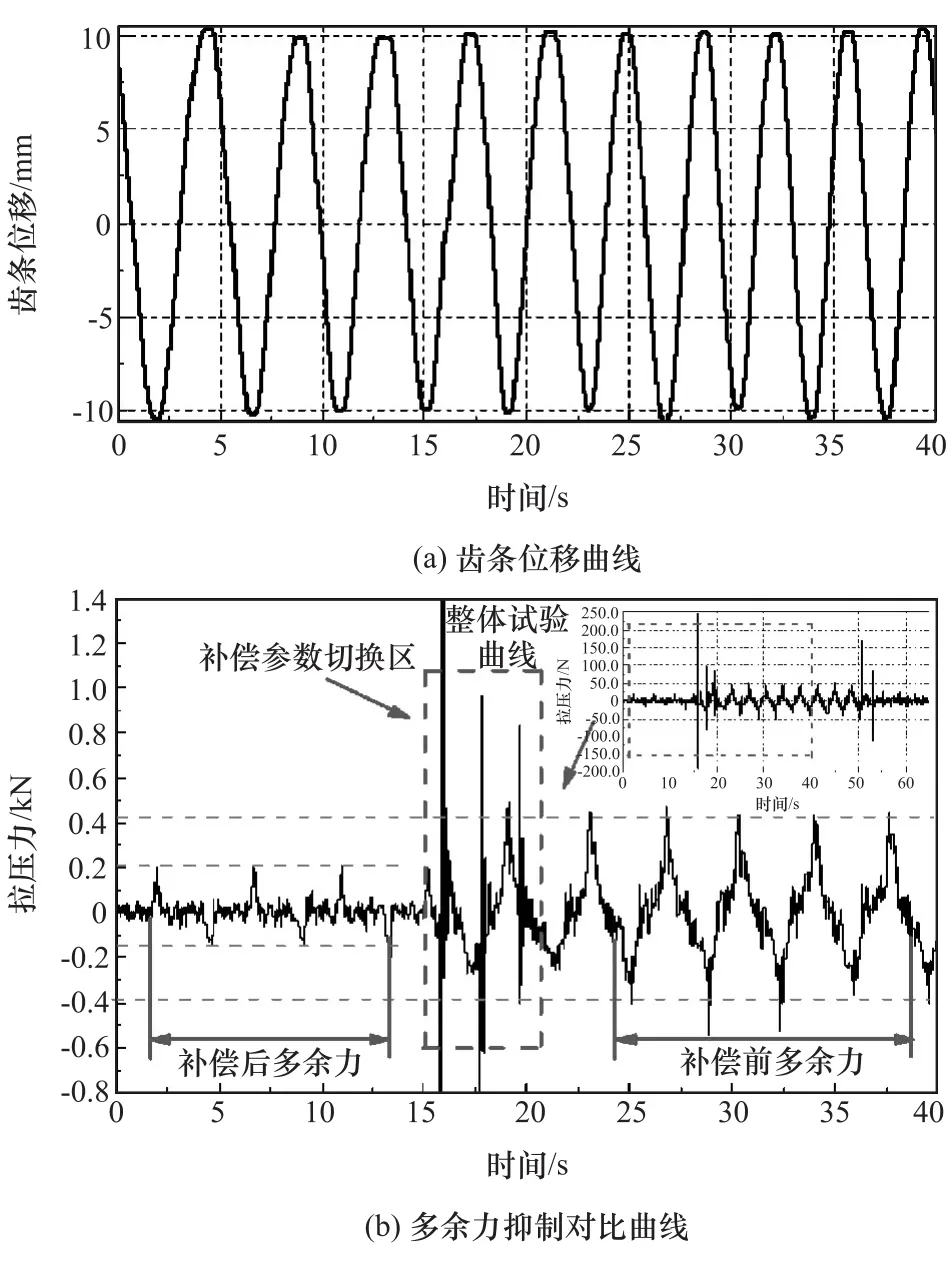
圖14 0.5Hz位移擾動下多余力抑制試驗曲線

6 結論

本文中針對轉向試驗臺的阻力加載控制問題進行研究。考慮加載系統機械傳動部件存在的摩擦和阻尼等非線性因素，通過力閉環控制提高阻力加載精度，同時利用串聯校正補償提高控制系統的穩定裕度。加載系統受齒條位移擾動產生多余力，文中進一步引入結構不變性原理和速度補償策略來抑制多余力的影響。仿真和臺架試驗結果表明，本文中提出的電動伺服系統阻力加載策略能快速地跟蹤目標值，同時可較好地抑制多余力對阻力加載精度的影響。

[1] HANSELMANN H.Hardware-in-the-loop simulation as a standard approach for development，customization and production test[C].SAE Paper 930207.

[2] LAWSON M，CHEN X.Hardware-in-the-loop simulation of fault tolerant control for an electric power steering system[C].Vehicle Power and Propulsion Conference(VPPC)，2008:1-6.

[3] 符文星，孫力，于云峰，等.大力矩電動負載模擬器設計與建模[J].系統仿真學報，2009，21(12):3596-3598.

[4] 鄒海峰，孫力，閻杰.飛行器舵機電動伺服加載系統研究[J].系統仿真學報，2004，16(4):657-659.

[5] 司丹丹，趙曉蓓，符文星，等.應用多路前饋和負反饋提高電動加載系統性能研究[J].測控技術，2008，27(5):90-93.

[6] 向海鷗.電控轉向硬件在環試驗臺開發與驗證[D].長春:吉林大學，2014.

[7] 季學武，馬小平，陳奎元.EPS系統性能試驗研究[J].江蘇大學學報(自然科學版)，2004，25(2):116-119.

[8] 余穎弘，王保華.汽車線控轉向硬件在環實驗臺研究現狀綜述[J].湖北汽車工業學院學報，2015(3):34-38.

[9] 穆桂脂.線控轉向前輪轉角控制策略硬件在環仿真研究[D].鎮江:江蘇大學，2009.

[10] 丁洋.基于dSPACE的SBW硬件在環仿真平臺開發[D].武漢:武漢科技大學，2013.

[11] 孫秀婕.電動負載模擬器智能控制技術研究[D].南京:南京航空航天大學，2012.

[12] 張健.基于RBF神經網絡的電動負載模擬器控制策略研究[D].哈爾濱:哈爾濱工業大學，2006.

[13] 方強.被動式力矩伺服控制系統設計方法及應用研究[D].哈爾濱:哈爾濱工業大學，2006.

[14] 劉曉東.電液伺服系統多余力補償及數字控制策略研究[D].北京:北京交通大學，2008.

[15] LI Yunhua.Development of hybrid control of electrohydraulic torque load simulator[J].Journal of Dynamic Systems，Measurement， and Control，2002，124:415-419.

[16] WANG Xingjian， WANG Shaoping， YAO Bin.Adaptive robust torque control of electric load simulator with strong position coupling disturbance[J].International Journal of Control，Automation， and Systems，2013，11(2):325-332.