基于ANSYS/LS-DYNA圓盤剪帶鋼剪切過程仿真研究

譚亮恩，陳益義(上海理工大學 機械工程學院，上海 200093)

0 引 言

圓盤剪是帶鋼精整作業線上的核心設備，圓盤剪按其功能分為切邊圓盤剪和分條圓盤剪，切邊圓盤剪主要用于帶鋼邊部缺陷的剪切，以滿足帶鋼寬度要求[1]。帶鋼剪切過程是包括材料變形及材料分離的塑性成型過程，刃口附件的板料受刀盤擠壓變形、斷裂，然而斷裂過程中一些復雜的現象無法通過解析法或實驗法得到有效解釋[2]。通過采用有限元法分析金屬塑性成型的剪切過程，不僅可以得到金屬塑性變形區的應力、應變分布情況以及帶鋼幾何形狀的變化過程，而且可以有效處理卸載問題，主要涉及材料的彈塑性行為、屈服準則、塑性流動法則、塑性強化準則、增量形式的彈塑性本構關系以及材料斷裂準則等幾個方面[3]。

本研究利用ANSYS/LS-DYNA有限元分析軟件，模擬帶鋼剪切過程，分析得到帶鋼斷裂過程中應力應變分布情況，導出剪切力的變化規律曲線，并將分析結果與剪切力實測值作比較，驗證有限元分析法對于求解剪切力的有效性。

1 圓盤剪的結構組成及工作原理

1.1 圓盤剪結構

圓盤剪的結構示意圖如圖1所示。

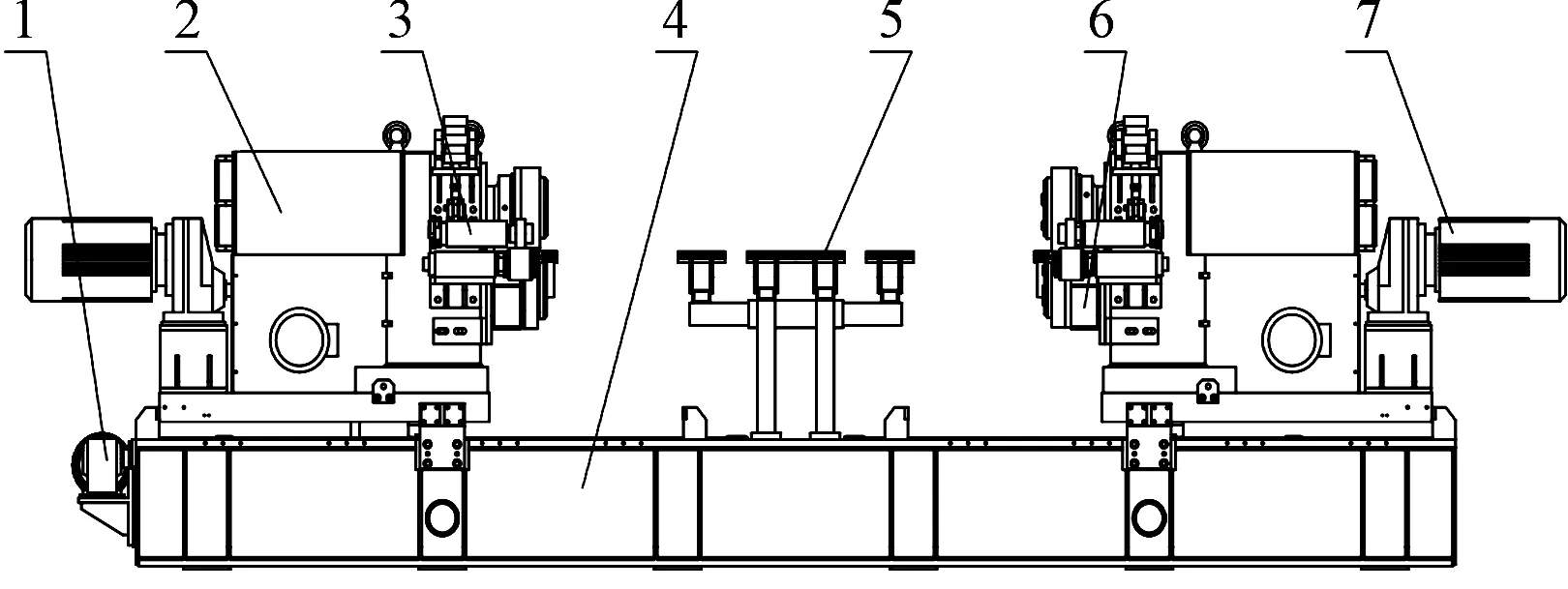
圖1 圓盤剪的結構示意圖1—機架開度調整機構；2—圓盤剪本體；3—去毛刺輥；4—底座；5—導板架；6—廢邊導槽；7—電機組成

圓盤剪主要由機架開度調整機構、圓盤剪本體、去毛刺輥、底座、導板架、廢邊導槽、電機組成[4]。其中，圓盤剪的核心部分是圓盤剪本體。

圓盤剪本體模型如圖2所示。

圖2 圓盤剪本體模型1—下刀軸；2—刀盤；3—上刀軸；4—側向間隙調整機構；5—重疊量調整機構；6—上刀座；7—下刀座；9—軸承；10—齒輪

本體主要由下刀軸、刀盤、上刀軸、側向間隙調整機構、重疊量調整機構、上刀座、下刀座、軸承、齒輪等組成。

1.2 圓盤剪工作原理

圓盤剪的工作過程包括：(1)確定來料帶鋼規格及工藝參數，帶鋼處于停止狀態；(2)根據帶鋼寬度，移動底座移動，調節機架開度；(3)根據帶鋼厚度，通過重疊量調整機構及側向間隙調整機構調整剪刃間隙，并通過測量確保間隙量的精準度；(4)機器啟動，帶鋼運動，進行邊部剪切；(5)帶鋼經過去毛刺輥輸出，廢邊進入廢邊導槽；(6)一個剪切周期完成，機器停止，帶鋼剪切完成。

1.2.1 帶鋼剪切過程模型

圓盤剪剪切帶鋼時，其兩對刀盤以帶鋼的運行速度為線速度做圓周運動，形成一對無端點的剪刃[5]。

圓盤剪剪切過程示意圖如圖3所示。

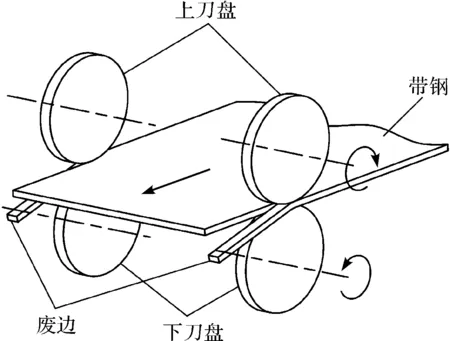
圖3 圓盤剪剪切過程示意圖

圓盤剪剪切過程中，隨著帶鋼的運行，上下刀盤的刃口距離逐漸減小，中間的板帶被不斷的擠壓切入，使板帶材料發生變形，最終被完全切斷。

1.2.2 帶鋼剪切區過程的3個階段和特點

帶鋼的剪切過程分為彈性變形階段、塑性變形階段和斷裂分離階段[6]，示意圖如圖4所示。

圖4 帶鋼剪切的3個階段

(1)彈性變形階段，如圖4(a)所示。帶鋼與上、下刀盤接觸并發生擠壓，接觸面產生彈性壓縮和穹彎，隨著帶鋼的運行，上、下刃口距離縮小，帶鋼的擠壓彎曲程度越厲害，但此時帶鋼受到的應力未超過材料的彈性極限，當上、下刀盤分離，帶鋼便可恢復原形。

(2)塑性變形階段，如圖4(b)所示。帶鋼繼續運行，刃口距離繼續變小，帶鋼變形逐漸加劇，當其內應力超過材料的屈服點時，金屬材料發生塑性變形，切口附近形成塌角區，當應力繼續增大，切口表面會形成光亮帶，由于剪刃間存在間隙，材料塑性變形的同時還伴有材料的彎曲和拉伸，材料內應力隨著剪切繼續進行而增大，刃口處應力集中加劇，當應力超過材料的斷裂極限時，帶鋼接觸面出現微小裂紋[7]。

(3)斷裂分離階段，如圖4(c)所示。隨著帶鋼切入深度的不斷增加以及剪切面積的減小，上、下刀盤刃口側面會先后產生裂紋，并且沿著最大切應力方向不斷擴展，當切入深度達到一定值時，上、下裂紋相互重合，材料隨即斷裂分離。

2 帶鋼剪切過程有限元分析

2.1 有限元模型建立

有限元模型的建立通過ANSYS中Model模塊實現。圓盤剪剪切有限元模型如圖5所示。

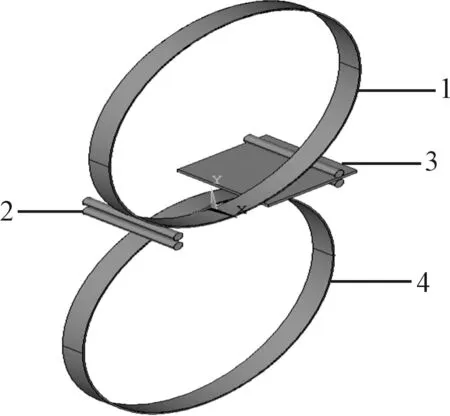
圖5 圓盤剪切有限元模型1—上刀盤；2—夾送輥；3—被剪切鋼板；4—下刀盤

模型包括上、下刀盤、帶鋼及夾送輥。其中，上、下刀盤簡化為半徑為250 mm，寬度為20 mm，厚度為3 mm的模型；鋼板尺寸取90 mm×90 mm×3 mm的方板；圓盤剪的出入口都加了夾送輥，夾送輥起輔助作用，對分析結果影響較小，因此對壓輥按原比例縮小為直徑為9 mm，長度為20 mm的圓柱體。另外，為了便于網格劃分，建模過程中將帶鋼被剪切部分進行了Divide操作。

2.2 選擇單元類型和定義材料模型

根據三維模型有限元分析實踐經驗，本文采用SOLID164單元進行模擬計算。SOLID164單元為六面體8節點單元，該單元類型共有兩種算法，分別為單點積分和全積分。對于單點積分算法而言，適用于材料大變形的研究，且計算時間短，其缺點是容易產生零能模態，需要進行沙漏控制[8]。本文采用單點積分，在分析計算過程中進行沙漏控制。

本研究采用剛體模型進行有限元分析。根據定義該模型需要輸入的參數有密度DENS、彈性模量EX、泊松比NUXY、平移約束參數Translational constant parameter、轉動約束參數Rotational constant parameter。根據帶鋼實際剪切過程，刀盤采用剛體模型，同時限制刀盤所有線性位移，限制刀盤繞Y軸、Z軸轉動約束，即只允許刀盤繞中心轉動[9]。

刀軸等材料性能參數如表1所示。

表1 材料性能參數設置

帶鋼采用的是塑性隨動材料模型，該模型可以是各向同性模型或隨動硬化模型，也可以是兼各向同性和隨動硬化特性為一體的混合模型。通過調整硬化參數大小來實現特性之間的轉換，同時，該模型的特點與應變率息息相關，通過Cowper-Symonds模型可以對該參數來進行計算和選擇，屈服應力可以用與應變率相關的參數來表示[10-11]，即：

(1)

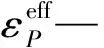
EP由下式給出：

(2)

鋼板材料采用各向同性硬化(β=1)材料模型，其Von Mises屈服條件是[12]：

(3)

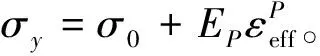
在定義時需要輸入彈性模量EX，密度DENS，泊松比NUXY，屈服應力σY，切線模量Etan，硬化參數β，應變率參數C和P以及失效應變εf。本文以剪切3 mm厚的08鋼為例。

具體材料性能參數如表2所示。

表2 計算所用材料性能參數

2.3 網格劃分

鑒于本研究所采用的SOLID164實體單元是六面體，且建立的分析模型中均為規則的圓柱體或立方體，因此本研究采用映射法進行網格劃分。

劃分單元后的有限元模型如圖6所示。

圖6 劃分網格后的有限元模型

如果剪刃側向間隙很小，剪切區單元太大，會使模擬結果不準確，單元太小又會使計算時間大大增加。經過調試發現，剪切區單元大小略小于剪刃側向間隙時為宜。

網格細分后的鋼板有限元模型如圖7所示。

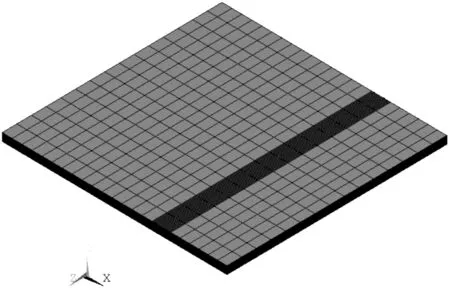
圖7 網格細化后的鋼板有限元模型

可見，整個有限元模型有著比較細致的區域劃分，能夠適應當前的計算需求。

2.4 定義接觸

本研究在ANSYS/LS-DYNA接觸選擇頁面中，對摩擦因數、接觸類型、接觸實體進行定義。摩擦因數主要包括有靜摩擦系數FS以及動摩擦系數FD。摩擦因數設置如表3所示。

表3 摩擦因數設置

在顯式動力學分析程序ANSYS/LS-DYNA中，接觸定義時采用PART ID號定義各部件之間的接觸。各PART號對應部件名稱如表4所示。

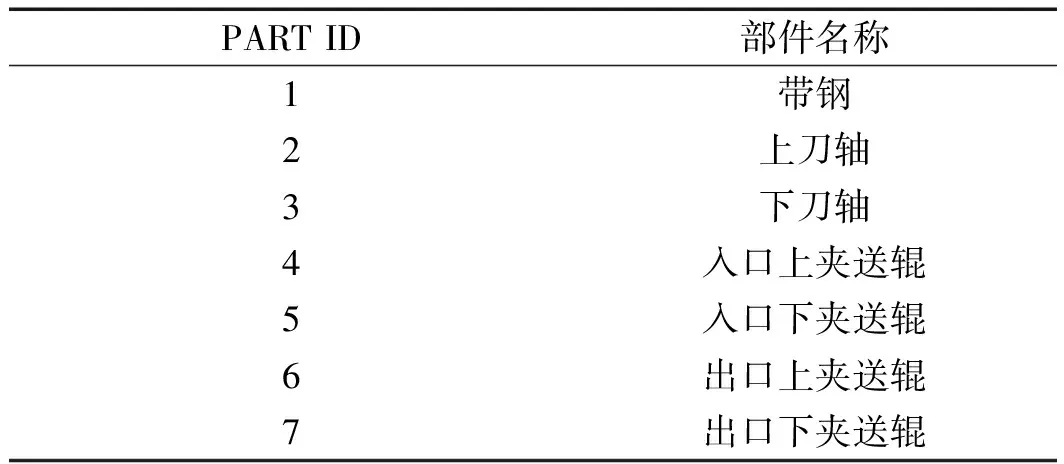
表4 PART號定義

實際剪切過程中，鋼板的上表面分別與上刀盤和上夾送輥發生接觸，鋼板的下表面分別與下刀盤和下夾送輥發生接觸。采用自動面面接觸(ASTS)定義各物體之間的接觸，自動面面接觸屬于雙向接觸，雙向接觸既檢查從節點對主面的穿透又檢查主面節點對從面的穿透，這樣對于主、從表面的定義是任意的。

2.5 添加載荷、初始條件、約束

本研究通過ANSYS/LS-DYNA程序對不同部件的不同部位施加特定的載荷。在施加載荷前，需要對承受載荷的部件進行定義，在一般情況下可以將其定義在PART號上。因此，ANSYS/LS-DYNA中定義載荷采用一對數組的方式，數組中包含兩部分，分別為時間和載荷。

為了較為真實地模擬帶鋼剪切過程，需要對零件受載方式做合理轉換。首先，本研究在上、下刀盤上分別施加相反方向的轉速，大小為3.125 r/s，模擬馬達驅動刀軸轉動。其次，在帶鋼前進方向施加500 mm/s的初速度，同時施加800 N的力，模擬夾送輥或卷取機對帶鋼的拉力作用。為了防止帶鋼在運動中左右移動，需要在帶鋼非傳動側施加對稱約束。

2.6 求解與求解控制

求解過程中需要對整個計算的物理過程進行分析，因此需要保證在剪切的過程中整個模型的長度大小與剪切的速度能夠做到完全匹配，這樣才能夠充分模擬整個剪刀的剪切過程。經計算后，計算時間設定為2.5 s。

求解時需要對輸出文件的輸出頻率進行設置，輸出頻率可以通過控制輸出步數實現，也可以通過設置各輸出文件的時間間隔實現。因時間間隔不好把握，本研究采用控制輸出步數的方法完成頻率的設置。

為了得到帶鋼剪切過程中剪切力的變化情況，可以通過帶鋼與刀盤間相互作用力實現。在計算時設置輸出Resultant forces，計算結果采用時間歷程ASCCII文件。ASCII輸出控制如圖8所示。

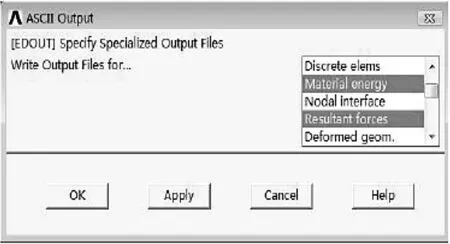
圖8 ASCII輸出控制

在求解過程中，需要保證LS-DYNA處在運行過程中，此時，可以利用操作輸入窗口來查看整個控制過程中的實時狀態變量。

可供選擇的選項如下：

輸入SW1。當整個ANSYS/LS-DYNA的計算程序終止運行時，會在另外一個程序中重新啟動一個新的文件。

輸入SW2。ANSYS/LS-DYNA程序播放和循環的次數都會在程序中進行顯示，當程序進行顯示時，相應的用戶就可以了解其計算進度和運行速度。

輸入SW3。ANSYS/LS-DYNA程序在運行的過程中會生成一個重啟文件，這個文件在特定的運行環境下會保持運行。

輸入SW4。ANSYS/LS-DYNA程序在運行完畢之后會自動生成一個結果，該結果可以保證整個進程完整運行。

采用LS-PREPSTD2.1和POST1后處理器，綜合處理模擬數據。

3 仿真結果分析

3.1 帶鋼剪切過程應力分析

帶鋼剪切過程Mises應力圖如圖9所示。

3.2 鋼板剪切過程塑性應變變化

整個等效剪切過程帶鋼塑性變形圖如圖10所示。

塑性變形過程中，帶鋼特性發生較大變化，從圖中可以清晰看到，塑性應變集中分布在剪縫處，距離剪縫越近，產生的塑性應變越大，最大塑性應變為0.397，而設定的失效應變為0.4，說明帶鋼斷裂過程中失效單元會被刪除，從而導致分析得到的塑性應變要比設定值小。

3.3 剪切過程中廢邊的運動規律

帶鋼豎直方向位移變化情況如圖(11～13)所示。

圖11 剪切開始時帶鋼的豎直方向位移圖

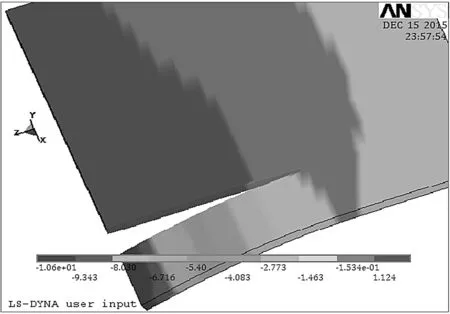
圖12 剪切過程中帶鋼的豎直方向位移圖

圖13 剪切完成時帶鋼的豎直方向位移圖

從圖12中可以清晰看出，經過上、下刀盤的擠壓，帶鋼發生斷裂，應力集中分布在剪切區域，最大等效應力出現在帶鋼斷裂縫隙處，大小為431 MPa。隨著距離剪切區越來越遠，等效應力相應減小，最小為0.4 MPa。同時，廢邊在自身重力下，自然向下彎曲，與現實中帶鋼剪切過程中的現象一致。

通過對比分析可以看出，隨著帶鋼的運行，廢邊產生下垂，廢邊初始段的位移逐漸增加，在3個時間點的垂直分量分別為-0.270 5 mm、-10.66 mm以及-36.2 mm，“-”號表示垂直分量的方向。伴隨著剪切過程的發展，在鋼板的兩邊都會產生劇烈的抖動和下垂的現象，這個與鋼板剪切的整個過程中的現象比較一致。

3.4 剪切過程中的剪切力變化

剪切過程中的剪切力變化如圖14所示。

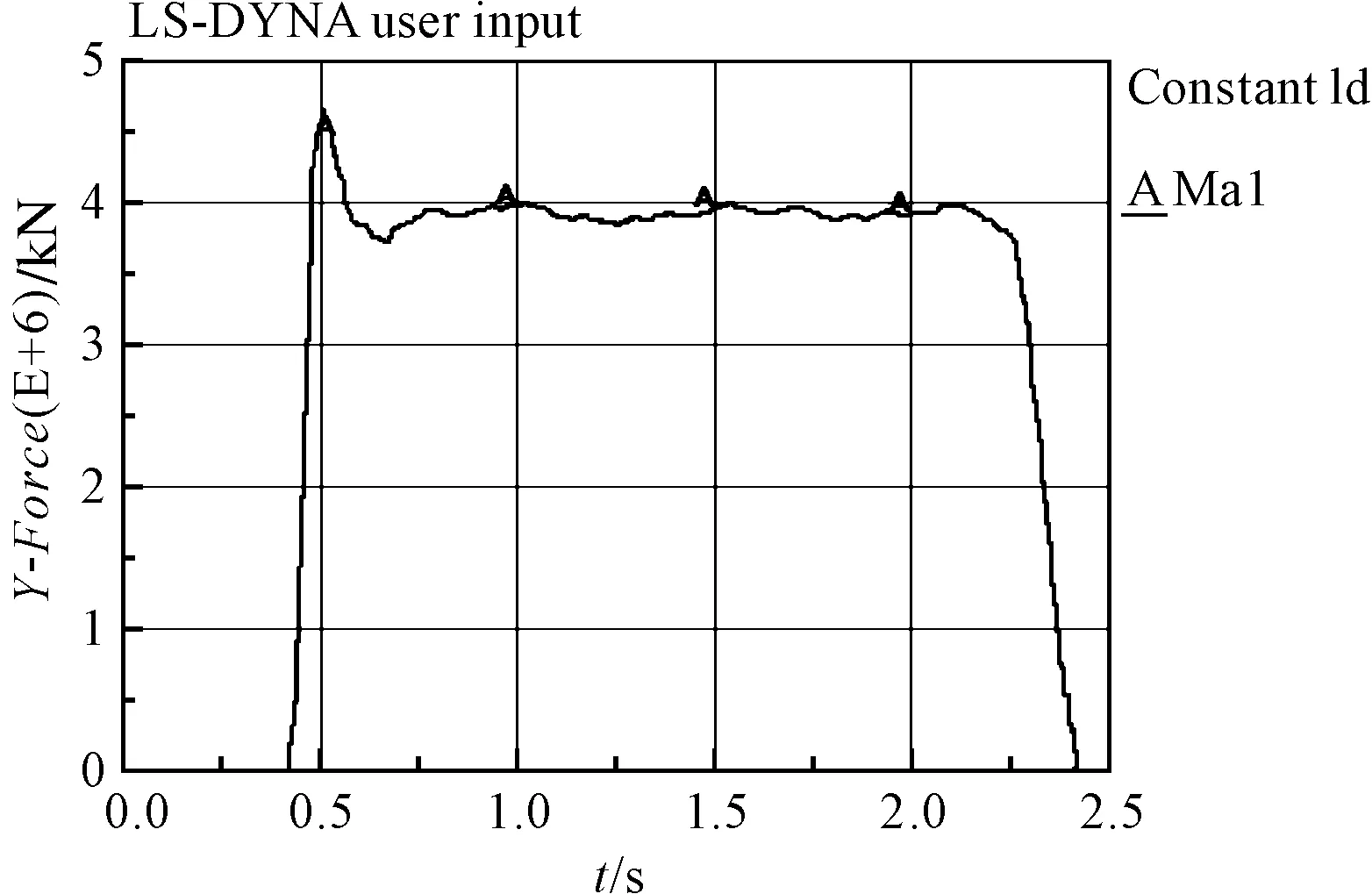
圖14 剪切力變化曲線圖

由圖14可見，剪切過程在0.4 s時，鋼板開始咬入，此時剪切力迅速增長，達到最大值4 463 N。咬入后剪切力逐漸減小，回落到4 000 N左右時保持基本穩定，并有周期性的波動，在2.4 s時剪切結束，剪切力減小為0。剪切過程中出現周期性小范圍的波動現象，這主要是因為剪切過程中上剪刃和帶鋼之間的有限元網格的接觸關系產生周期性的變化，且剪切過程中鋼板會發生擺動。

4 結束語

針對圓盤剪帶鋼剪切質量不高，且同時剪切過程中一些復雜的現象無法通過解析法或實驗法得到有效解釋的問題，本研究根據圓盤剪帶鋼剪切過程的變形特點,基于有限元分析理論，利用ANSYS/LS-DYNA，建立了切邊圓盤剪剪切帶鋼的有限元仿真模型,對帶鋼動態剪切過程進行了彈塑性有限元分析。結論如下：

(1)帶鋼剪切過程中，應力集中分布在剪切區域，最大等效應力出現在帶鋼斷裂縫隙處，大小為431 MPa，隨著距離剪切區越來越遠，等效應力會相應減小，最小為0.4 MPa；

(2)隨著帶鋼的運行，廢邊產生下垂，廢邊初始段的位移逐漸增加，伴隨著剪切過程的發展，在鋼板的兩邊都會產生劇烈的抖動和下垂的現象，與鋼板剪切的實際過程中的現象是一致的；

(3)剪切過程中，剪切力變化規律為：咬入時剪切力急速增大到最大值4 463 N，咬入后剪切力快速回落到4 000 N左右時保持基本穩定，并有周期性的波動，在剪切完成時剪切力快速回落至0。

[1] 張愛華,呂 杰.國內主要鋼廠冷軋汽車板競爭態勢分析[J].冶金經濟與管理,2015(5):11-19.

[2] 楊桂通.彈塑性力學引論[M].北京:清華大學出版社,2013.

[3] 肖 磊,郭坤龍.影響圓盤剪帶材剪切質量的因素分析[J].上海有色金屬,2014,35(1):30-32.

[4] 鄒家祥.軋鋼機械[M].北京:冶金工業出版社,2011.

[5] 黃慶學.軋鋼機械設計[M].北京:冶金工業出版社,2007.

[6] SAANOUNI K. 3D numerical simulation of anisotropic thin sheet metal slitting process using fully coupled constitutive equations including ductile damage[J].InternationalJournalMaterialForming,2009,2(1):535-538.

[7] 溫 彤,陳 霞.金屬板材剪切變形全過程的模擬[J].模具技術,2006(4):3-6.

[8] 王勖成.有限單元法[M].北京:清華大學出版社,2003.

[9] 曾 攀.有限元分析及應用[M].北京:清華大學出版社,2004.

[10] 石現景,鍍鋅板圓盤剪分切加工過程有限元仿真與實驗研究[D].廣東:廣東工業大學機電工程學院,2014.

[11] 張 淵，陳 睿，張文棟，等.基于ANSYS的齒輪泵泵體有限元分析[J].液壓氣化與密封，2017(3)：43-46.

[12] 賈海亮.圓盤剪剪切過程的有限元模擬和實驗研究[D].太原:太原科技大學機電工程學院,2007.