梁板式高樁碼頭時變承載力研究

龍俞辰，印宇軒

(中交第四航務工程勘察設計院有限公司，廣州 510220)

1 時變承載力影響因素

本文將高樁碼頭時變承載力的影響因素分為兩類：一類統計量隨時間變化，統稱為“承載力衰減性影響因素”；另一類統計量不隨時間變化、或變化緩慢的影響因素，統稱為“承載力隨機性影響因素”。

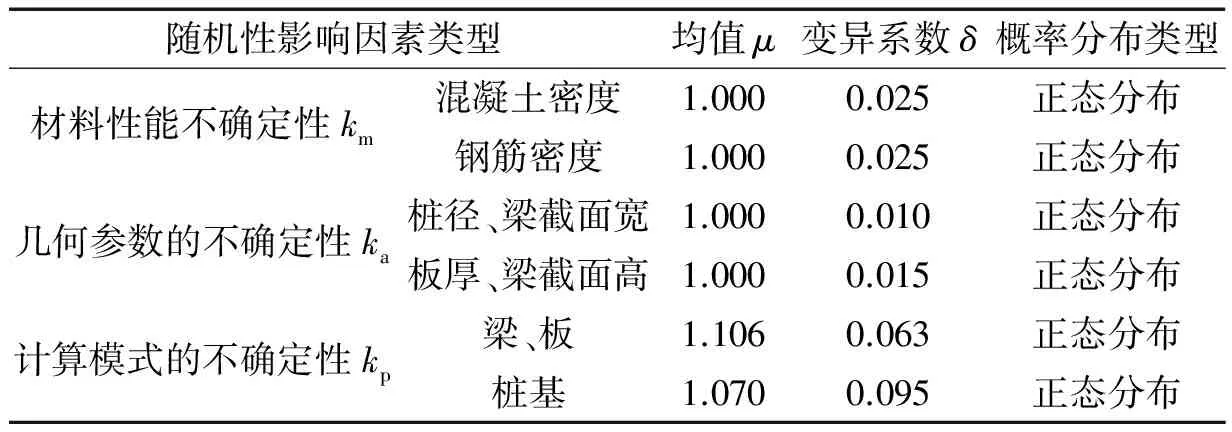
表1 隨機性影響因素統計參數及概率分布Tab.1 Probability distribution and statistical parameter of randomness-influencing factor

1.1 承載力隨機性影響因素

常見結構承載力隨機性影響因素分為材料性能、幾何參數和計算模式的不確定性，如表1所示。

1.2 承載力衰減性影響因素

一般而言，鋼筋混凝土結構的抗氯離子侵蝕耐久性壽命可分為如下三個階段：(1)銹蝕誘導：t=0結構開始暴露于海洋環境，氯離子逐漸侵蝕，段末t=ti鋼筋表面氯離子濃度達到臨界值Ccr；(2)銹蝕發展：t=ti鋼筋開始銹蝕，段末t=tcor混凝土保護層開裂；(3)剩余壽命：t=tcor鋼筋與腐蝕環境直接接觸，段末達到承載能力極限狀態。綜合國內外研究成果，本文認為承載力衰減性影響因素為：(1)銹蝕導致的鋼筋強度降低、截面減小；(2)鹽類腐蝕導致的混凝土強度降低；(3)鋼筋銹蝕物及混凝土膨脹開裂導致的鋼-混粘結強度降低。

1.2.1 鋼筋初始銹蝕時間

結合氯離子的傳輸過程Fick第二定律、擴散系數D(t)模型[1]，以及鋼筋銹蝕的初始條件和邊界條件，可以得到結構內部的氯離子濃度表達式

(1)

式中：C為氯離子濃度；x為結構內部相對于表面的距離；t為結構投入使用的時間；D0為在t0時刻的實測擴散系數；α為與水灰比W/Ce有關的經驗系數，α=3×(0.55-W/Ce)；Cs為混凝土表面氯離子濃度。

表2 湛江港t0=10 a實測氯離子擴散系數(10-8cm2/s)Tab.2 t0=10 a, Measurement of D0 in Zhanjiang Port

(1) 實測氯離子擴散系數D0。王勝年等[2]給出了湛江港暴露十年的試件的氯離子擴散系數，結果見表2。

缺少實測數據的情況下可采用Life-365程序中所提出的D0計算公式

D0=10-12.06+2.4W/C

(2)

(2)表面氯離子濃度CS。Thomas在文獻[3]中建議無實測數據時，可按照表3進行CS的取值。

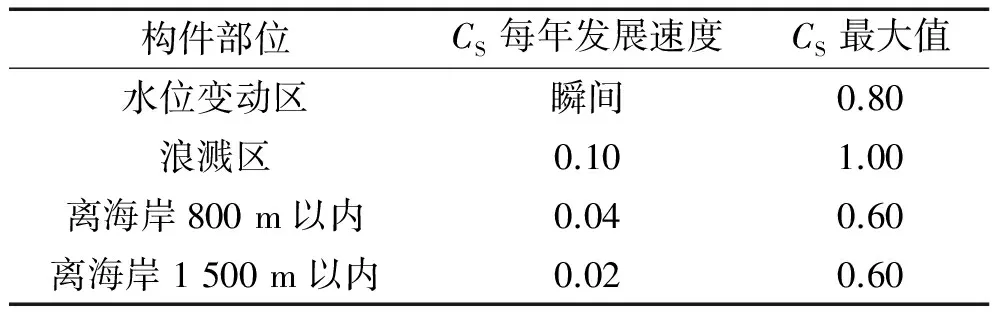
表3 氯鹽環境CS經驗取值(占混凝土重量百分比，%)Tab.3 Experience value of CS in chlorine salt environment

(3)臨界氯離子濃度Ccr。國內外對臨界氯離子濃度Ccr進行了多次研究，具體結果見表4[4]。

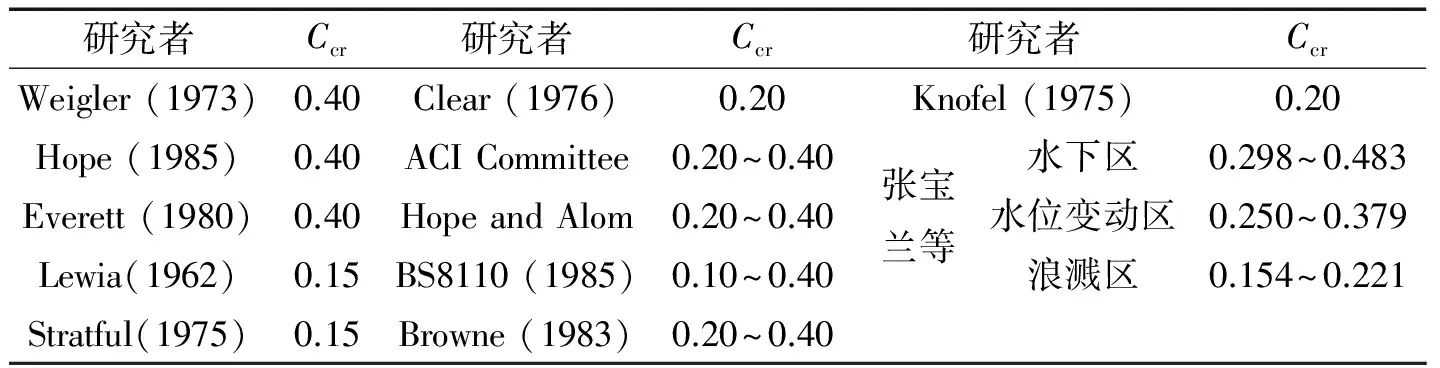
表4 臨界氯離子濃度Ccr(占混凝土重量百分比，%)Tab.4 Critical chloride concentration Ccr

當鋼筋表面的氯離子濃度達到臨界濃度時，則鋼筋開始銹蝕，對最外側的鋼筋銹蝕開始時間可以通過下式求解

C(c,ti)=Ccr

(3)

式中：ti為銹蝕開始時間；c為保護層厚度。

1.2.2 混凝土開裂時間

(4)

式中：tcor為從鋼筋開始銹蝕到保護層開裂的時間；Wcr為臨界鋼筋銹蝕量；V為鐵銹生成速度；ω為與銹蝕產物相關的系數；d為鋼筋直徑；icor為銹蝕電流。

(5)

式中：ρrust，ρst分別為鐵銹密度3 600 kg/m3和鋼筋密度7 850 kg/m3；c為保護層厚度；ft為混凝土抗拉強度；υc為混凝土泊松比，一般取0.17；h為鋼-混界面空隙厚度，取12.5 μm；Wst為銹蝕鋼筋質量，Wst=ωWcr，若鐵銹為Fe(OH)3，ω=0.523，若鐵銹為Fe(OH)2，ω=0.622，鐵銹為二者混合物，ω=0.57；Eef為混凝土有效彈性模量，Eef=Ec/(1+φcr)，Ec為混凝土彈性模量，φcr為混凝土徐變系數，早強水泥取2.2，普通水泥取2.0。

本文采用文獻[5]建立的Kim-Li鋼筋銹蝕速度模型

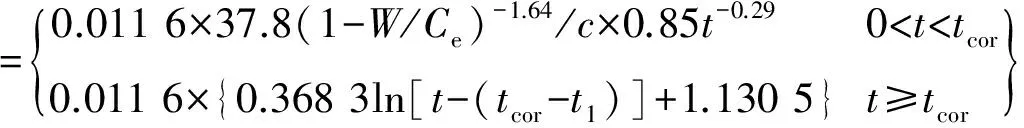
(6)

式中：λ(t)為鋼筋銹蝕速度，mm/a；t1為銹蝕速度時間連續性的相對時間點。按式(7)求解t1

(7)

1.2.3 承載力衰減性影響因素

(1)銹蝕鋼筋截面積As(t)。鋼筋截面積的時程函數如下所示

(8)

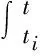
(9)

式中：As(t)為鋼筋截面積；d0為銹蝕前的鋼筋直徑；d(t)為t時刻鋼筋直徑。

文獻[6]對港工構件的鋼筋橫截面幾何尺寸進行了參數統計，確定銹蝕鋼筋截面積ka的均值為1.0、變異系數為0.03、服從正態分布，結合式(8)可以確定鋼筋截面積在任意時刻的均值、標準差以及概率分布。

(2)銹蝕鋼筋強度fy(t)。銹蝕鋼筋的實際屈服強度fy可以表示為

fy(t)=ky(t)fy,0

(10)

(11)

式中：ky(t)為鋼筋屈服強度的降低系數[7]；fy,0為銹蝕前鋼筋屈服強度；kl為鋼筋截面損失率，按下式計算

(12)

文獻[5]統計得出鋼筋強度的隨機性如表5所示。

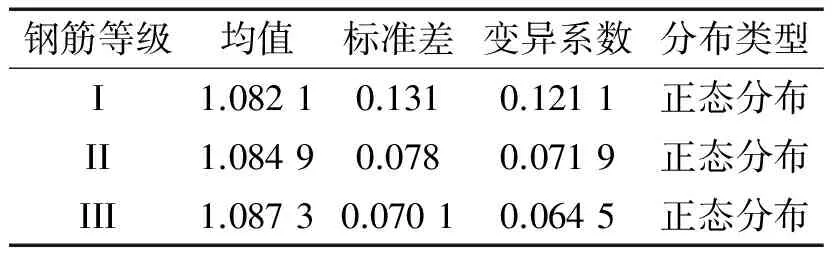
表5 鋼筋強度km統計參數Tab.5 Statistical parameter of km of reinforcement yield strength

綜上，鋼筋屈服強度的隨機過程模型得以確定。

(3)混凝土強度fc(t)。文獻[8]根據海洋環境長期暴露試驗和實際建筑物測試結果建立了混凝土立方體抗壓強度隨機過程模型

(13)

式中：μfcu(t)，σfcu(t)分別為第t年混凝土立方體抗壓強度的均值、標準差；μfcu,0，σfcu,0分別為第28 d混凝土立方體抗壓強度的均值、標準差。根據文獻[9]可知

表6 混凝土立方體抗壓強度的變異系數[9]Tab.6 Coefficient of variation of cube compressive strength of concrete[9]

fcu,k=μfcu,0(1-1.645δfcu,0)

(14)

式中：fcu,k為混凝土立方體抗壓強度的標準值。

綜上，混凝土強度的隨機過程模型得以確定。

(4)鋼混粘結強度ks(t)。文獻[10]根據試驗結果給出了基于鋼筋銹蝕程度的粘結強度系數的計算公式

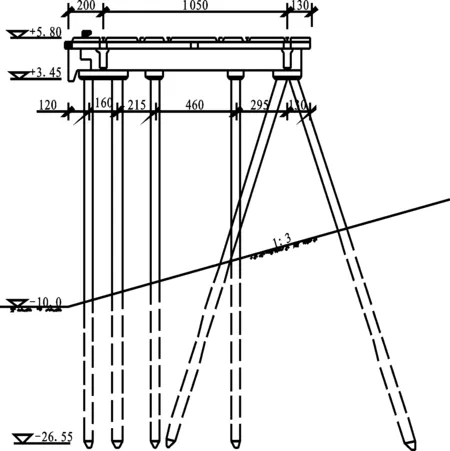
圖1 碼頭模型典型斷面圖Fig.1 Typical cross section of open type wharf on piles

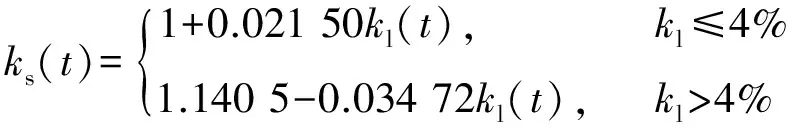
(15)

1.3 算例

1.3.1 碼頭模型

梁板式高樁碼頭模型排架間距7 m，碼頭上部結構采用C40混凝土，水灰比0.5；樁基采用C40混凝土，水灰比0.45；主筋采用HRB335。面板、樁基主筋保護層厚度50 mm；縱橫梁主筋保護層厚度60 mm。面板板厚550 mm，長邊6 800 mm，橫梁上擱置長度200 mm，短邊3 000 mm，縱梁上擱置長度100 mm，主筋配筋率0.006。橫梁截面600 mm×1 200 mm，底部配筋率0.008，頂部配筋率0.002。軌道梁截面550 mm×1 100 mm，底部配筋率0.008，頂部配筋率0.002。樁基截面550 mm×550 mm，總樁長30 m，主筋配筋率0.015。

1.3.2 碼頭模型臨界時間計算結果

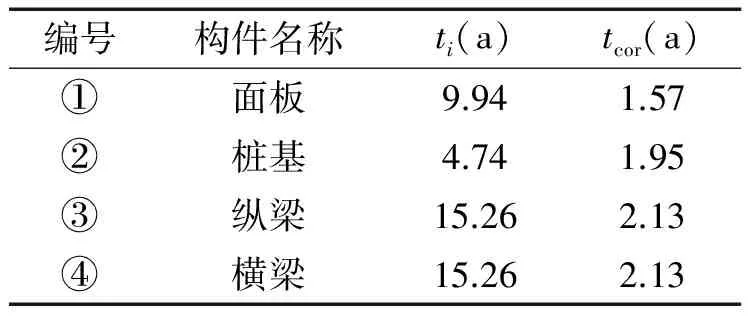
表7 碼頭構件臨界時間計算結果Tab.7 Critical time for components of wharf

結合1.2.1節各式可得碼頭模型鋼筋初始銹蝕時間ti；結合1.2.2節各式可得碼頭模型混凝土開裂時間tcor，計算結果如表7所示。

1.3.3 碼頭模型衰減性影響因素計算結果

結合1.2節內容，可計算得到C40強度時變結果如表8所示,以及模型各構件的時變參數結果如表9所示。

表8 C40強度時變計算結果

Tab.8 Time-dependent strength of C40

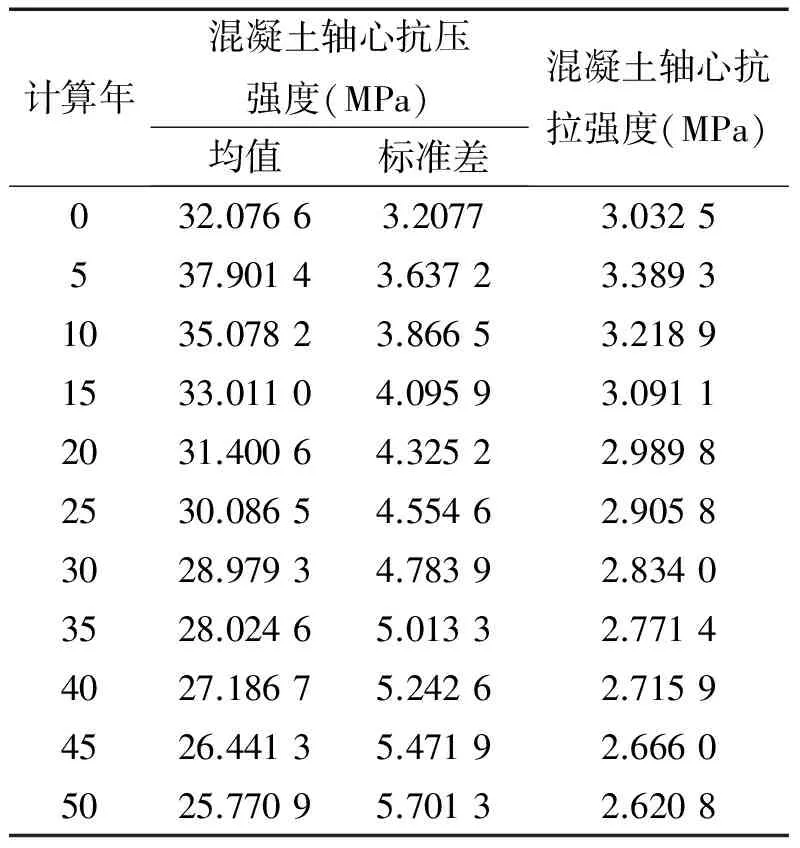
計算年混凝土軸心抗壓強度(MPa)均值標準差混凝土軸心抗拉強度(MPa)032．07663．20773．0325537．90143．63723．38931035．07823．86653．21891533．01104．09593．09112031．40064．32522．98982530．08654．55462．90583028．97934．78392．83403528．02465．01332．77144027．18675．24262．71594526．44135．47192．66605025．77095．70132．6208

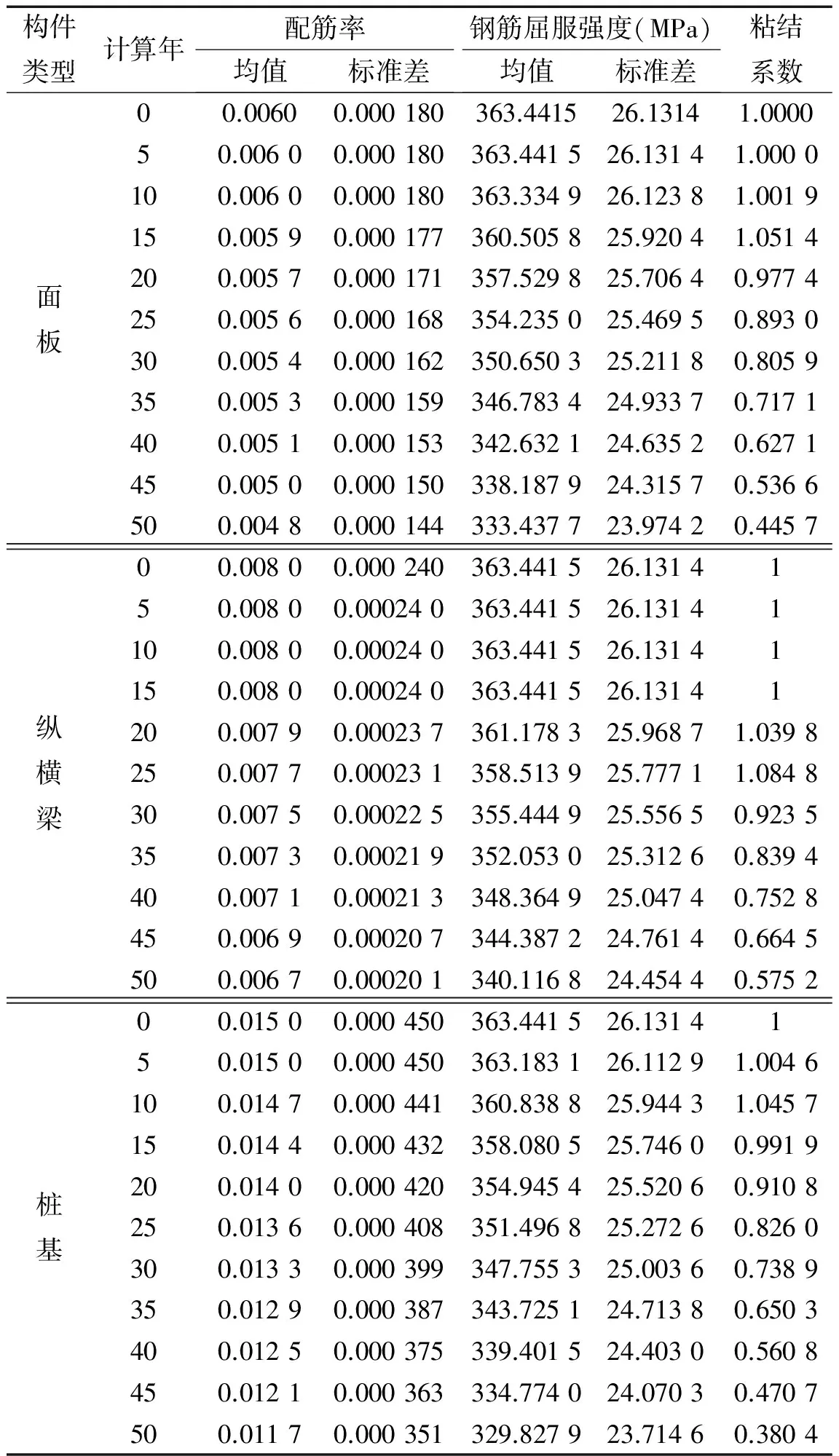
表9 碼頭模型構件參數時變計算結果Tab.9 Time-dependent parameter of components of model

2 碼頭構件承載力隨機過程

2.1 承載力隨機過程模型

常用于描述分布類型恒定的結構承載力的隨機過程為

(16)

式中：R(t)為結構承載力隨機過程；R0為結構承載力初值隨機變量；φ(t)為承載力衰減函數；μR(t)為時變承載力均值；δR(t)為時變承載力變異系數；μR0為初始承載力均值；δR0為初始承載力變異系數。

任意時刻構件時變承載力隨機過程退化為服從對數正態分布的隨機變量，其概率密度函數fR(r,t)可表示為

(17)

按照規范構件承載力R(t)的解析式可表示為

(18)

式中：Rp(t)為結構計算承載力；fi(t)為材料性能參數；Ai(t)為幾何參數。根據統計數學的誤差傳遞原理

(19)

式中：Xi為材料性能或幾何參數。通過式(18)和式(19)可求出該時刻構件承載力的統計參數，通過求解對多個時間點的構件承載力統計參數，可確定高樁碼頭構件承載力的衰減函數。

2.2 碼頭構件承載力衰減函數

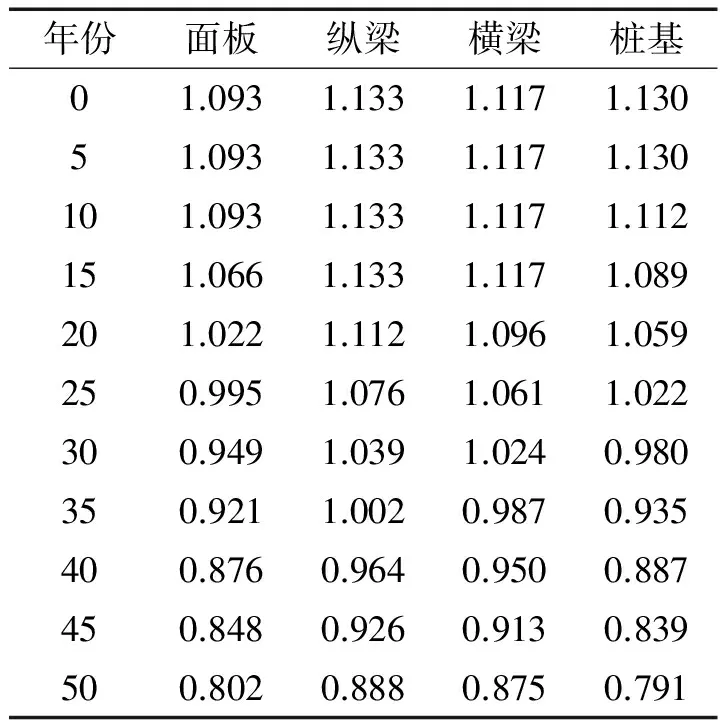
表10 碼頭構件承載力αR均值計算結果Tab.10 Mean value of αR of components of wharf

為了使統計參數值更具廣泛性，對承載力進行無量綱化處理

αR=R/RK

(20)

式中：αR為無量綱化承載力；R為承載力實際值隨機變量；Rk為承載力標準值。

對于高樁碼頭構件，面板、縱橫梁按受彎構件考慮，樁基按受壓構件考慮。結合1.3小節的碼頭模型構件參數的時變計算結果，可以計算得出時變承載力如下表10所示。

計算所得的各個構件承載力的變異系數：面板0.080，橫梁0.073，縱梁0.076，樁基0.082。

如前所述，本文中對于高樁碼頭構件承載力隨機過程采用統一的模型式(16)來描述。由上表可以得到構件承載力在多個時刻的衰減函數值如表11所示。

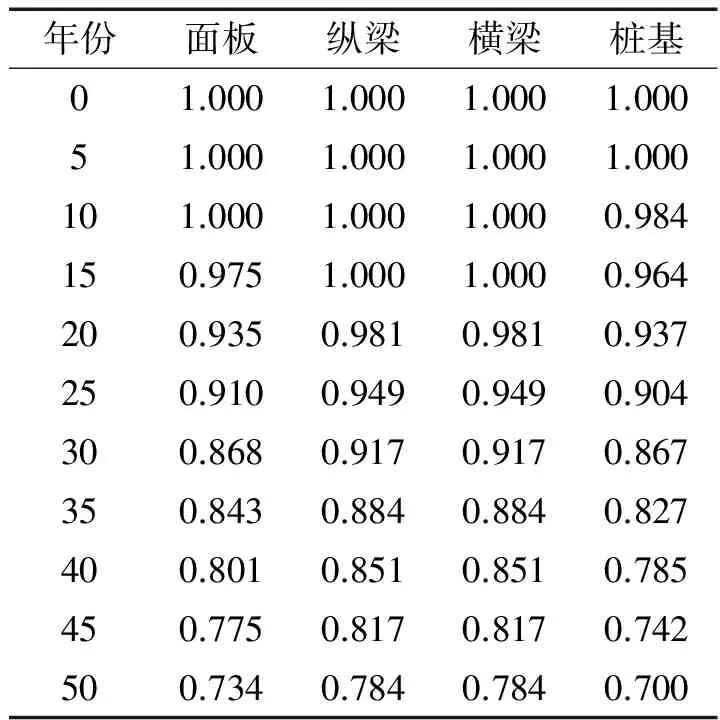
表11 構件承載力衰減函數值Tab.11 Value of attenuation function at multiple time points

選取如下四種函數對各構件承載力衰減函數進行擬合，擬合結果如表13～表16所示。

表12 擬合函數選取Tab.12 Selection of fitting functions

表13 面板承載力衰減函數擬合Tab.13 Fitting of attenuation function for slab

表14 縱梁承載力衰減函數擬合Tab.14 Fitting of attenuation function for longitudinal beam

表15 橫梁承載力衰減函數擬合Tab.15 Fitting of attenuation function for transverse beam

表16 樁基承載力衰減函數擬合Tab.16 Fitting of attenuation function for pile foundation

上述各表中的SSE為殘差平方和，R2為判定系數，兩個系數均用于分析曲線的擬合優度。SSE越小，R2越大，則認為擬合的效果越好。故各表從上至下為最優擬合至最差擬合。可以看出，對于四種高樁碼頭構件，承載力衰減函數的最優擬合均為分子為一次多項式、分母為二次多項式的有理式。

3 結論

本文第1節介紹了影響高樁碼頭構件承載力隨機過程的兩類因素，即“承載力隨機性影響因素”和“承載力衰減性影響因素”，詳細闡述了各個因素的基本概念以及它們對承載力的影響等。通過算例可以看出，本文既定性描述了各個影響因素的含義，又定量地確定了各個影響因素的統計值。本文第2節闡述了建立高樁碼頭構件承載力隨機過程的步驟，并分析確定了高樁碼頭各類構件的承載力衰減函數均最適合采用分子為一次多項式、分母為二次多項式，共有四個系數的有理式進行描述。從而，只要確定碼頭構件在初始時刻以及其他任意三個時刻的承載力，便可以完全確定構件承載力隨機過程，進而可以用于評估高樁碼頭構件的時變可靠度。

[1]Mangat P S, Molly B T. Prediction of long term chloride concentration in concrete[J]. Materials and Structures, 1994, 27(7)：338-346.

[2]王勝年,黃君哲,張舉連,等.華南海港碼頭混凝土腐蝕情況的調查與結構耐久性分析[J].水運工程,2000(6):8-12.

WANG S N, HUANG J Z, ZHANG J L, et al. An Investigation on Concrete Corrosion of Seaport Wharf in South China and Analysis of Structures′ Durability[J]. Port&Waterway Engineering, 2000(6):8-12.

[3]M.D.A. Thomas and Bentz E.C.Life-365: Computer program for predicting the service life and life-cycle costs of reinforced concrete exposed to chlorides[C]//American Concrete Institute. Committee 365, Service Life Prediction. Detroit: Michigan, 2001.

[4]Chun Qing Li. Initiation of chloride-induced reinforcement corrosion in concrete structural members-Prediction[J]. ACI Structural Journal, 2002(2):133-141．

[5]孫藝.海洋環境下高樁碼頭耐久性分析方法研究[D].天津:天津大學,2005.

[6]《港口工程結構可靠度設計統一標準》編制組.港口工程結構可靠度[M].北京:人民交通出版社,1992.

[7]沈德建,吳勝興.海水浪濺下混凝土中銹蝕鋼筋性能試驗研究及仿真分析[J].工業建筑,2005,35(3):58-62.

SHEN D J, WU S X. Experimental study and simulation analysis on corroded bars in concrete at the marine cycle[J]. Industrial Construction, 2005,35(3):58-62.

[8]牛荻濤. 海洋環境下混凝土強度的經時變化模型[J].西安建筑科技大學學報,1995,27(1):49-52．

NIU D T. Changing models of concrete strength along with time in marine environment[J]. Xi′an Univ. of Arch.&Tech., 1995,27(1):49-52．

[9]JTJ267-98, 港口工程混凝土結構設計規范[S]．

[10]何世欽.氯離子環境下鋼筋混凝土構件耐久性能試驗研究[D].大連:大連理工大學,2004.