黃土耕作農(nóng)田地表土壤(0～2 cm)容重的多元非線性預(yù)報模型

郭李娜，樊貴盛

(太原理工大學(xué)水利科學(xué)與工程學(xué)院，山西 太原 030024)

0 引 言

地表土壤作為直接與外界交換物質(zhì)和能量的媒介，對降雨、灌溉入滲、地面徑流和土壤侵蝕過程的影響非常顯著，進而對深層土壤中水分、鹽分及養(yǎng)分的運移產(chǎn)生影響和改變，最終會影響到農(nóng)作物的整個生長發(fā)育過程。地表土壤容重表征了地表土壤的密實程度和孔隙度，是預(yù)測田間水分利用率、水分入滲率和作物需水量的重要參數(shù)之一。在降雨條件下，地表土壤容重變化引起地表水文狀況的變化，從而間接影響土壤水分和溶質(zhì)的擴散速率和遷移過程[1]。據(jù)Kaur[2]、Bernoux[3]、Tomasella和Hodnett[4]等報道，控制土壤容重的主要因素是土壤質(zhì)地，次要因素是有機質(zhì)含量。而對地表土壤容重來說，由于對外界環(huán)境的敏感性導(dǎo)致其影響因素是多方面的，程詩念等研究發(fā)現(xiàn)：在黃土地區(qū)大降雨發(fā)生后，地表土壤受雨水擊打和浸濕后濕陷變形大，容重明顯增大[5]。張西超等報道灌水量與土壤容重呈現(xiàn)顯著的相關(guān)關(guān)系[6]。馮棣通過多年的大田定位咸水灌溉試驗得出咸水灌溉導(dǎo)致土壤積鹽，表層土壤容重增加的結(jié)論[7]。

土壤容重作為農(nóng)業(yè)生產(chǎn)中重要的物理參數(shù)，其測量方法通常有環(huán)刀法、量積法和蠟封法，但都不適用于大面積農(nóng)田土壤容重的持續(xù)跟蹤采樣與監(jiān)測。近年來，國內(nèi)外學(xué)者利用土壤常規(guī)理化參數(shù)，通過土壤容重傳遞函數(shù)對土壤容重進行預(yù)測，在很大程度上解決了這一問題。Kaur等基于印度4個流域土壤的樣本數(shù)據(jù)，建立了土壤容重與土壤質(zhì)地及有機碳含量的土壤容重傳遞函數(shù)模型[8]。韓光中等利用現(xiàn)有的土壤數(shù)據(jù)庫回歸分析建立了我國主要土壤類型最適宜的容重傳遞函數(shù)[9]。王巧利[10]等以復(fù)合圓錐指數(shù)儀為工具，建立了BP神經(jīng)網(wǎng)絡(luò)的土壤容重預(yù)測模型。

縱觀國內(nèi)外學(xué)者通過土壤傳遞函數(shù)預(yù)測土壤容重的研究，多以自然土壤容重為主，且輸入變量較少，尤其沒有考慮降雨、灌溉水量的影響，即降雨、灌溉水量作為主要輸入變量，對地表土壤容重進行多元非線性預(yù)測的模型鮮見。本文在前人研究的基礎(chǔ)上，針對黃土耕作農(nóng)田地表土壤(0～2 cm)容重，從分析地表土壤容重與各影響因素之間關(guān)聯(lián)關(guān)系入手，考慮增加累積接收水量和全鹽量等因素作為輸入變量，建立了地表土壤容重(0～2 cm)的多元非線性預(yù)報模型，實現(xiàn)了利用常規(guī)土壤理化參數(shù)和累積接收水量對地表土壤容重的多變量預(yù)測，豐富了土壤傳輸函數(shù)理論的發(fā)展。

1 材料與方法

1.1 試驗區(qū)概況

試驗區(qū)橫跨山西省中部的十五個縣市區(qū)，北緯34°34′～40°44′，東經(jīng)110°15′～114°32′之間，海拔600～2 000 m。試驗區(qū)均被疏松黃土廣泛覆蓋，年度跟蹤試驗點布設(shè)在山地、平原、盆地等多種地貌類型區(qū)。該區(qū)屬于溫帶季風(fēng)氣候，年均氣溫多在3.96～13.99 ℃之間，多年平均降雨量364～618 mm，無霜期為124～232 d。試驗區(qū)土壤體積含水率在0.78%～50.25%之間，種 植作物類型有冬小麥、蔬菜和玉米，種植冬小麥的試點在作物生長期內(nèi)灌水3次，分別在10月和第二年的4月、5月，平均灌溉定額為265 mm；種植蔬菜的試點約20 d灌溉一次，平均灌溉定額為360 mm；種植玉米的試點多數(shù)無灌溉，部分試點在7月和9月灌溉兩次，平均灌溉定額為170 mm。試驗區(qū)相關(guān)指標(biāo)與0～2 cm土壤基本理化參數(shù)變化范圍見表1。

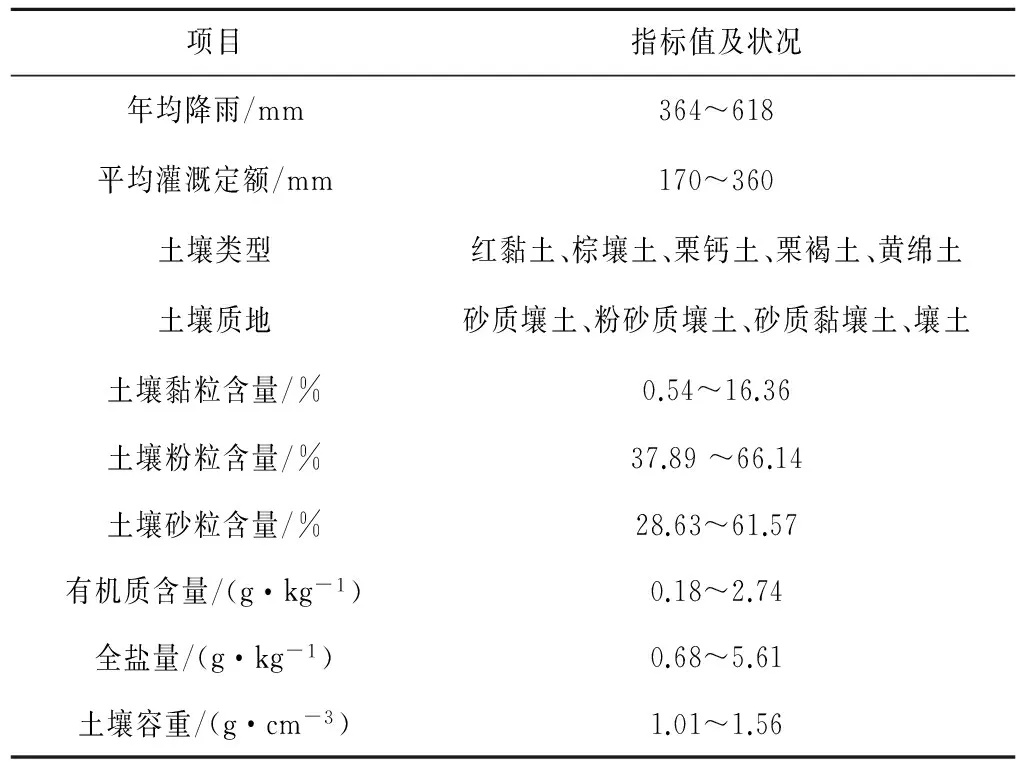
表1 試驗區(qū)土壤狀況及基本理化參數(shù)指標(biāo)

1.2 試驗方案與方法

試驗從2015年4月下旬開始到2015年11月中旬結(jié)束，監(jiān)測頻次為每15 d左右一次，包括大田耕作地表土壤容重、降雨量、灌溉量和土壤基本理化參數(shù)的跟蹤測定。

地表土壤容重采用環(huán)刀法進行測定，所用環(huán)刀為高度2 cm，直徑5 cm的非標(biāo)準(zhǔn)環(huán)刀。土壤累積接收水量即為試驗區(qū)累積降雨量和灌溉量之和，其中試驗區(qū)降雨量采用氣象站設(shè)施觀察得到，灌溉量通過記錄當(dāng)?shù)剞r(nóng)戶農(nóng)事作業(yè)資料獲得。

測定的土壤基本理化參數(shù)包括土壤含水率、土壤質(zhì)地、土壤有機質(zhì)含量和土壤全鹽量。各參數(shù)的測定方法：土壤含水率測定采用烘干稱重法，再經(jīng)容重值換算成體積含水率；土壤質(zhì)地通過篩分+比重計法得到篩分曲線，然后分析土壤的顆粒級配得到；土壤有機質(zhì)含量的測定采用重鉻酸鉀滴定法來測定[11]；土壤全鹽量測定通過殘渣烘干質(zhì)量法測定。

1.3 樣本數(shù)據(jù)的建立

基于整理后的地表土壤容重與土壤基本理化參數(shù)共同構(gòu)成的系列試驗數(shù)據(jù)樣本，確定156組作為建模樣本，8組作為所建預(yù)測模型的檢驗樣本。其中5組由地表(0～2 cm)土壤容重和相對應(yīng)的土壤黏粒含量、粉粒含量、有機質(zhì)含量、體積含水率、全鹽量和累積接收水量等參數(shù)構(gòu)成的數(shù)據(jù)樣本如表2所示。

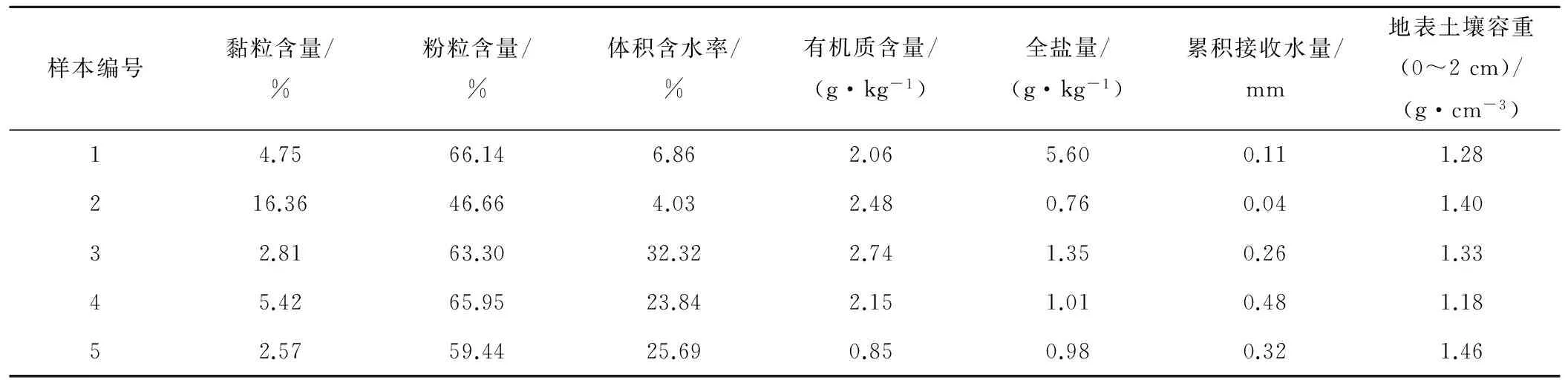
表2 試驗點代表組樣本數(shù)據(jù)

2 地表土壤容重的多元非線性模型的建立

2.1 模型輸入、輸出變量的確定

2.1.1 地表土壤容重的影響因素分析

前人以往的研究表明：影響土壤容重的主要因素有土壤質(zhì)地、有機質(zhì)含量和土壤含水率等，其機理不再贅述。筆者的研究認為土壤容重除以上所述影響因素外，還受降雨量、灌溉水量、全鹽量和農(nóng)民耕作活動等因素的影響。

降雨和灌溉對地表土壤容重有較大影響，一方面是由于雨滴對地表土壤的機械擊打壓實作用明顯，破壞了土壤中由較小顆粒團聚成的團聚體，分散的土粒會進入土壤的孔隙從而減小了孔隙度，使得土壤的密實度增大，改變了土壤的容重；另一方面是因為黃土具有濕陷性和壓實性，降雨或灌溉后地表土壤浸水，水分沿著黃土的孔隙和節(jié)理直接入滲到土壤內(nèi)部，結(jié)構(gòu)中的架空孔隙發(fā)生崩塌，土體顆粒隨孔隙的塌陷而向下沉降，孔隙率降低，地表土壤容重發(fā)生改變。為反映降雨和灌溉長期對地表土壤容重的影響，筆者試圖將時段內(nèi)的降雨量和灌溉量進行累加得到試驗點累積接受水量，并選作本文預(yù)報模型的輸入變量之一。

土壤全鹽量是指土壤中水溶性鹽的總量，一般取八大常用離子含量之和。土壤中可溶性鹽含量的升高，特別是Na+質(zhì)量分數(shù)的增加，使更多吸附在土壤膠體上的Ca2+和Mg2+被Na+置換到土壤溶液中，更易產(chǎn)生絮狀沉淀堵塞土壤空隙，使土壤的孔隙度變小；同時土壤膠體在交換性Na+的作用下水化度增大，土壤顆粒膨脹度和分散度增大導(dǎo)致土壤中大孔隙結(jié)構(gòu)崩塌，孔隙率降低，最終導(dǎo)致地表土壤容重的增大。

2.1.2 影響因子模糊關(guān)聯(lián)度分析

上文通過定性分析確定了地表土壤容重的5個影響因素，分別是土壤質(zhì)地、有機質(zhì)含量、體積含水量、累積接收水量和全鹽量。但各個影響因子與地表土壤容重間的關(guān)聯(lián)程度如何需要研究分析。在試驗數(shù)據(jù)資料中隨機選取30組數(shù)據(jù)作為計算樣本，其中采用土壤黏粒含量、粉粒含量和砂粒含量表征土壤質(zhì)地，以地表0～2 cm土壤容重值為參考序列，各影響因子為比較序列，利用灰色關(guān)聯(lián)理論[12,13]求出灰色關(guān)聯(lián)度，以此來描述因素間關(guān)系的強弱和次序，為合理地選擇多元非線性預(yù)報模型的輸入因子提供依據(jù)。排序結(jié)果見表3。

表3 地表土壤容重影響因子關(guān)聯(lián)度計算結(jié)果表

由表3可知，各輸入?yún)?shù)與γ間的關(guān)聯(lián)度均在0.7以上，關(guān)聯(lián)程度較好，可作為地表土壤容重預(yù)報模型的輸入變量，關(guān)聯(lián)度排序為β1>Q>L>β2>θ>β3>ψ。

根據(jù)上述分析，最終選定關(guān)聯(lián)度較好的土壤黏粒含量β1及土壤粉粒含量β2、有機質(zhì)含量Q、體積含水率θ、累積接收水量L和全鹽量ψ作為本文多元非線性預(yù)報模型的輸入變量。

2.1.3 預(yù)測變量確定

黃土耕作農(nóng)田地表(0～2 cm)土壤容重為本研究多元非線性預(yù)報模型的輸出變量。

2.2 多元非線性模型的建立

多元非線性預(yù)報模型是一種可以同時擬合多個獨立自變量和因變量間非線性函數(shù)關(guān)系的預(yù)報模型，其實質(zhì)是通過擬合各個自變量的單因素擬合方程，確定自變量與因變量間的獨立的函數(shù)關(guān)系，并將各個自變量與因變量的獨立函數(shù)關(guān)系進行線性疊加，通過T值檢驗，舍棄掉影響較小的自變量，并最終確立主導(dǎo)自變量和因變量之間的函數(shù)方程。

2.2.1 地表土壤容重與各影響因子單因素函數(shù)形式

基于實測資料，在保證其他影響因素相同或接近的前提下，對數(shù)據(jù)進行篩選，重復(fù)選取5～10組滿足要求的數(shù)據(jù)，采用MATLAB中的Cftool工具，繪制散點圖和回歸曲線圖，圖1-圖6為其中擬合度較好的幾種情況。

在對多組數(shù)據(jù)重復(fù)進行回歸和擬合后，參考離散點的走勢和擬合度的大小，最終確定各因素與地表土壤容重的最佳回歸方程形式，見表4。

由表4所得到的單因素最優(yōu)回歸方程的形式可知：在其他因子相同或接近相同時，地表土壤容重與土壤黏粒含量β1和 粉粒含量β2均呈現(xiàn)線性關(guān)系；地表土壤容重與土壤有機質(zhì)含量Q、體積含水率θ和全鹽量ψ存在對數(shù)關(guān)系；地表土壤容重與累積接收水量L呈現(xiàn)非線性關(guān)系。

表4 地表土壤容重與各影響因子單因素函數(shù)形式

2.2.2 多元非線性模型形式確定

多元非線性模型是指機械疊加各個單因素形式，在此基礎(chǔ)上確定出輸出參數(shù)與多個輸入?yún)?shù)多元非線性形式，從而確定地表土壤容重與多個影響因素之間的非線性形式，具體形式為式(1)所示：

γ=c0+c1β1+c2β2+c3lnθ+

c4lnQ+c5lnψ+c6L2+c7L

(1)

式中：c0代表模型的常數(shù)項；c1代表自變量β1的系數(shù)；c2代表自變量β2的系數(shù)；c3代表自變量lnθ的系數(shù)；c4代表自變量lnQ的系數(shù)；c5代表自變量lnψ的系數(shù)；c6代表自變量L2的系數(shù)；c7代表自變量L的系數(shù)。

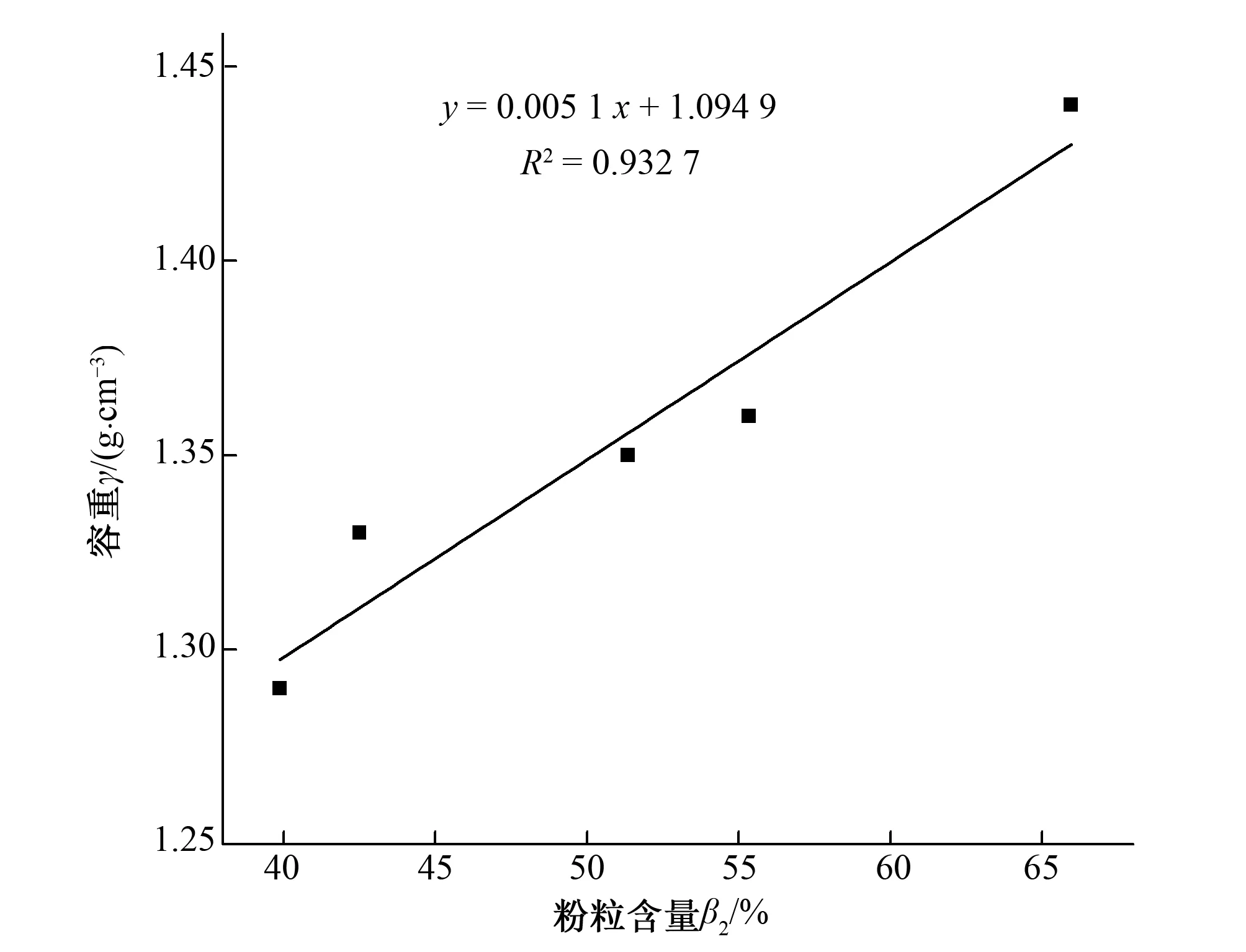
圖1 地表土壤容重與黏粒含量的單因素函數(shù)形式

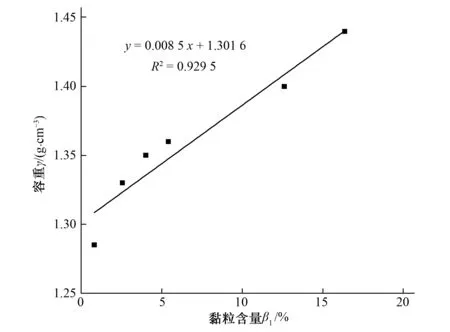
圖2 地表土壤容重與粉粒含量的單因素函數(shù)形式

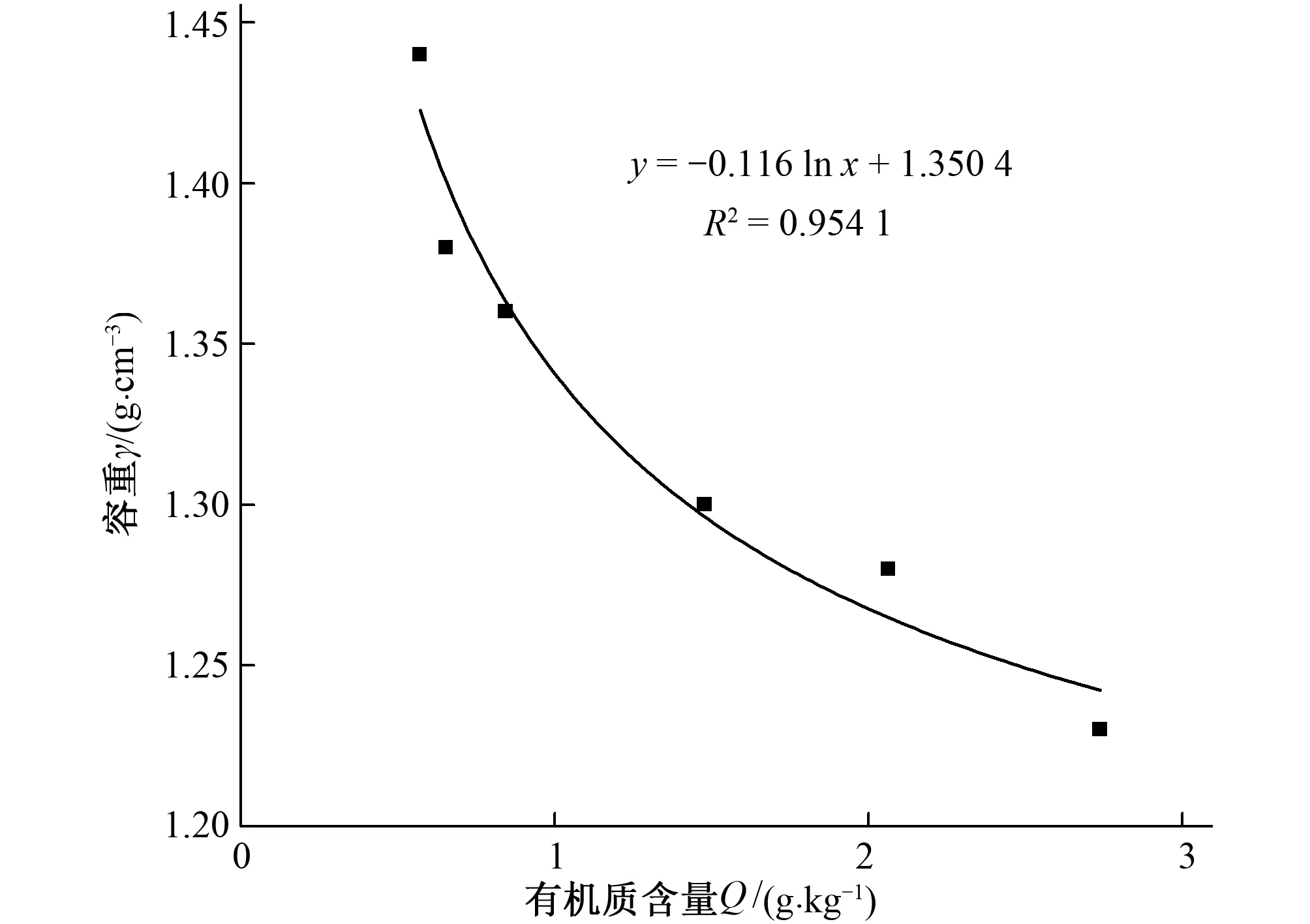
圖3 地表土壤容重與有機質(zhì)含量的單因素函數(shù)形式

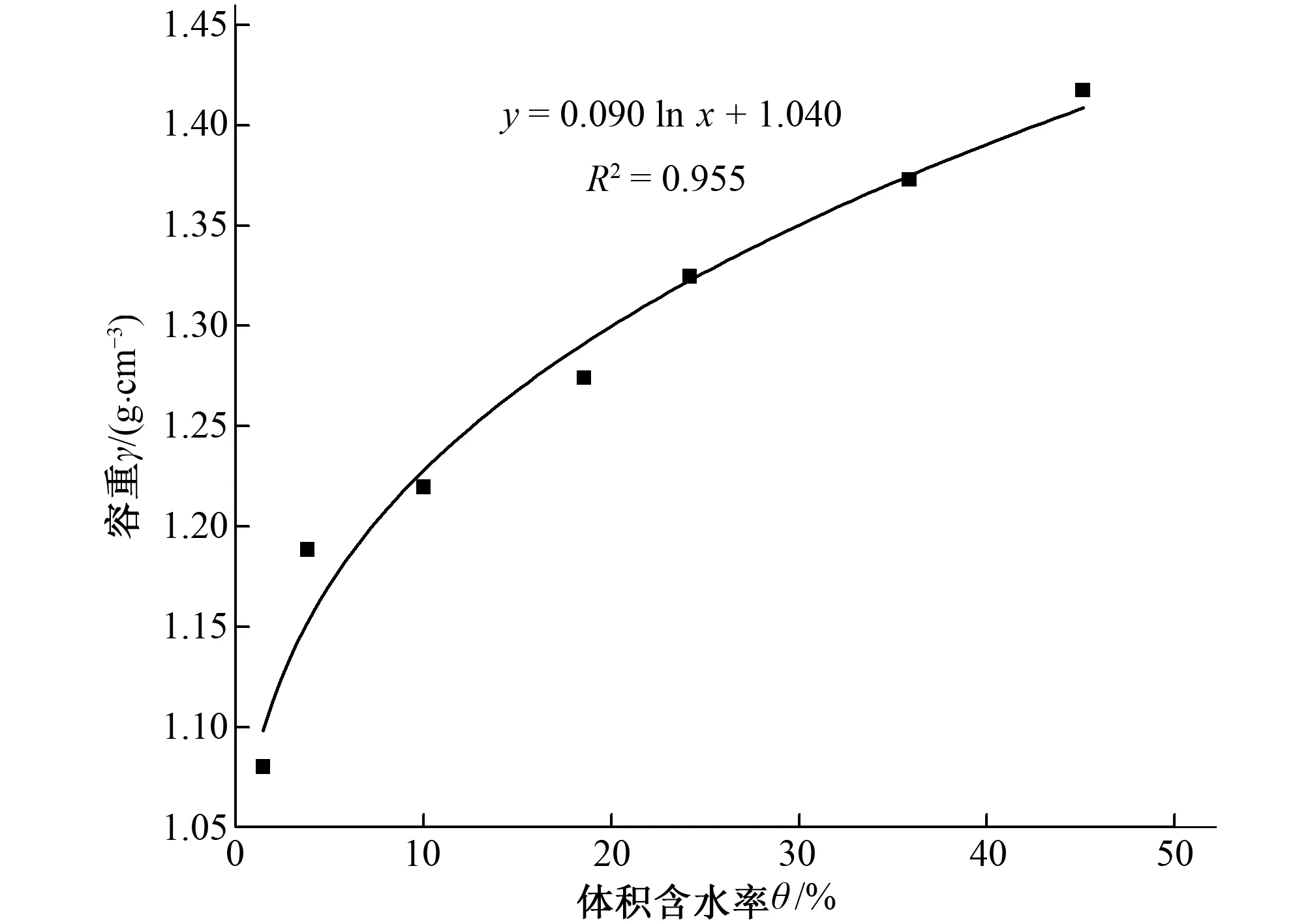
圖4 地表土壤容重與體積含水率的單因素函數(shù)形式

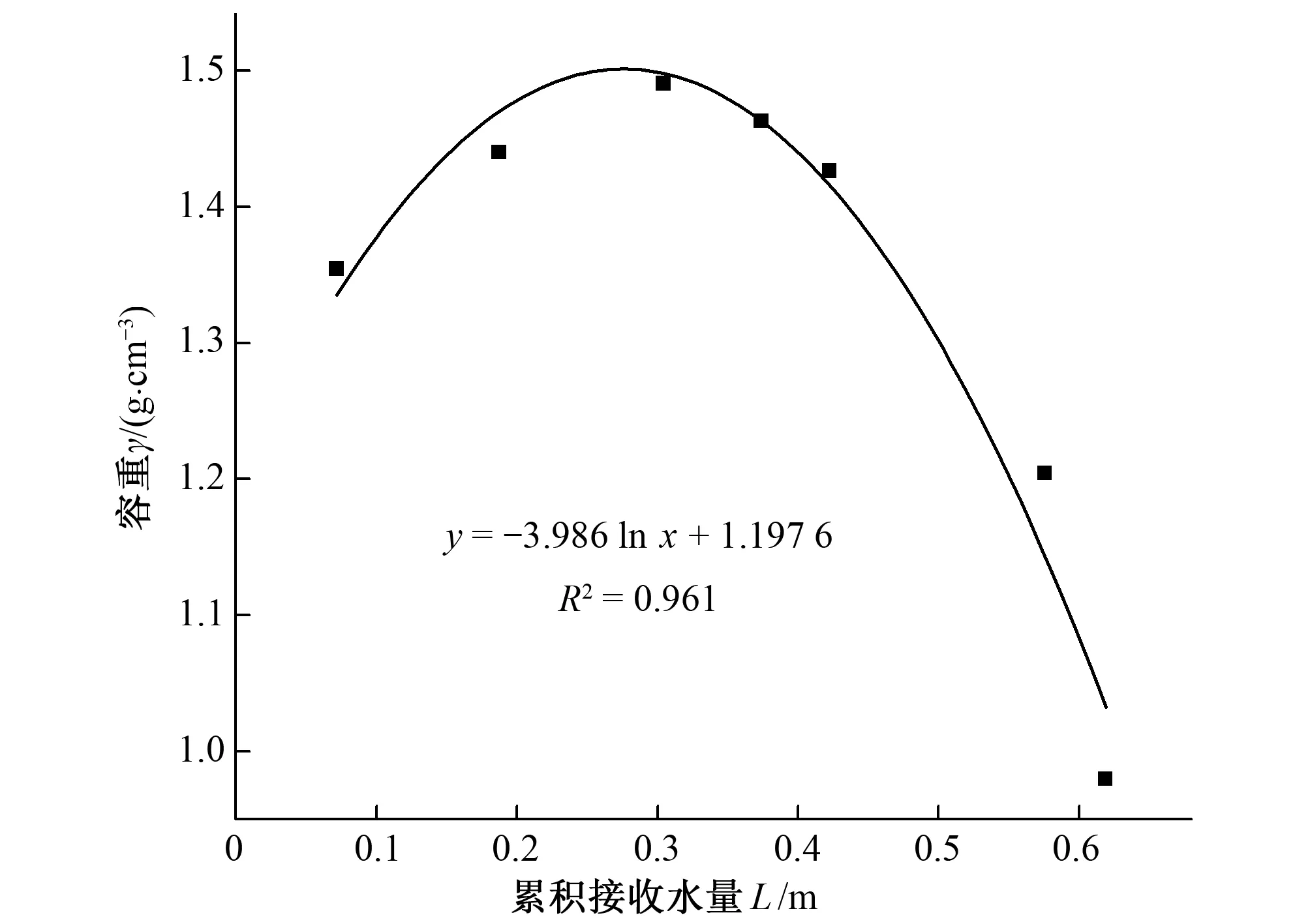
圖5 地表土壤容重與累積接收水量的單因素函數(shù)形式

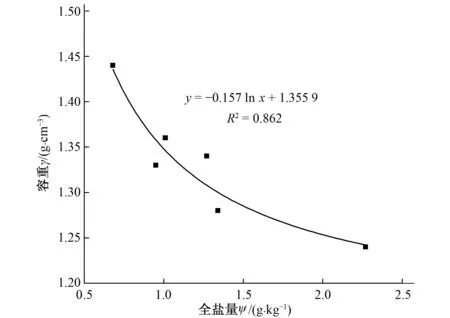
圖6 地表土壤容重與全鹽量的單因素函數(shù)形式

2.2.3 模型自變量T檢驗

利用MATLAB非線性預(yù)報模型中的T檢驗程序，依次對模型中每個輸入因子進行T檢驗，檢驗要求為|T|≥T0.05/2(查表得T0.05/2=2.014 4)，滿足此條件的輸入因子是影響地表土壤容重的主要因子，可作為本文所建立非線性傳輸函數(shù)的輸入因子，全部T檢驗完成后，最終確定非線性預(yù)報模型的所有輸入?yún)?shù)，檢驗結(jié)果如表5所示。

表5 地表土壤容重回歸方程自變量T值檢驗表

由以上T檢驗分析結(jié)果可知，本文所選擇的影響地表土壤容重的6個參數(shù)的T值均大于T0.05/2，故均通過T檢驗，由此確定γ的多元非線性方程自變量為β1、β2、lnθ、lnQ、lnψ、L2、L，且通過擬合計算得到各自變量的系數(shù)值，得到非線性模型如式(2)所示：

γ=1.139 9+(0.754 1β1)+(0.252 1β2)+

(0.043 3 lnθ)-(-0.028 7 lnQ)+(-0.060 1 lnψ)+

(-0.770 4L2)+0.745 2L

(2)

化簡后最終得到的非線性模型如式(3)所示：

γ=1.139 9+0.754 1β1+0.252 1β2+0.043 3 lnθ+

0.028 7 lnQ-0.060 1 lnψ-0.770 4L2+0.745 2L

(3)

2.2.4 地表土壤容重非線性模型顯著性檢驗

根據(jù)選取的156組試驗樣本數(shù)據(jù)，通過計算得到表征回歸方程顯著性的F值，并與給定顯著性水平α=0.05下的F值(查表得F0.05(m，n-m-1)=2.07，m=7，n=156)進行對比，對上述得到的地表土壤容重非線性模型的顯著性進行檢驗。若計算得到的F>F0.05，則表明預(yù)測模型顯著。計算結(jié)果如表6所示。

表6 多元非線性模型檢驗結(jié)果

通過上述檢驗分析結(jié)果可知，γ非線性回歸模型的F值遠大于F0.05，所建回歸方程的顯著性強，預(yù)測模型的可信度高。

3 非線性模型精度檢驗

3.1 建模樣本非線性模型精度檢驗

計算建模的156組樣本數(shù)據(jù)預(yù)測值與實測值間的相對誤差，并進行精度對比，計算結(jié)果如表7所示。

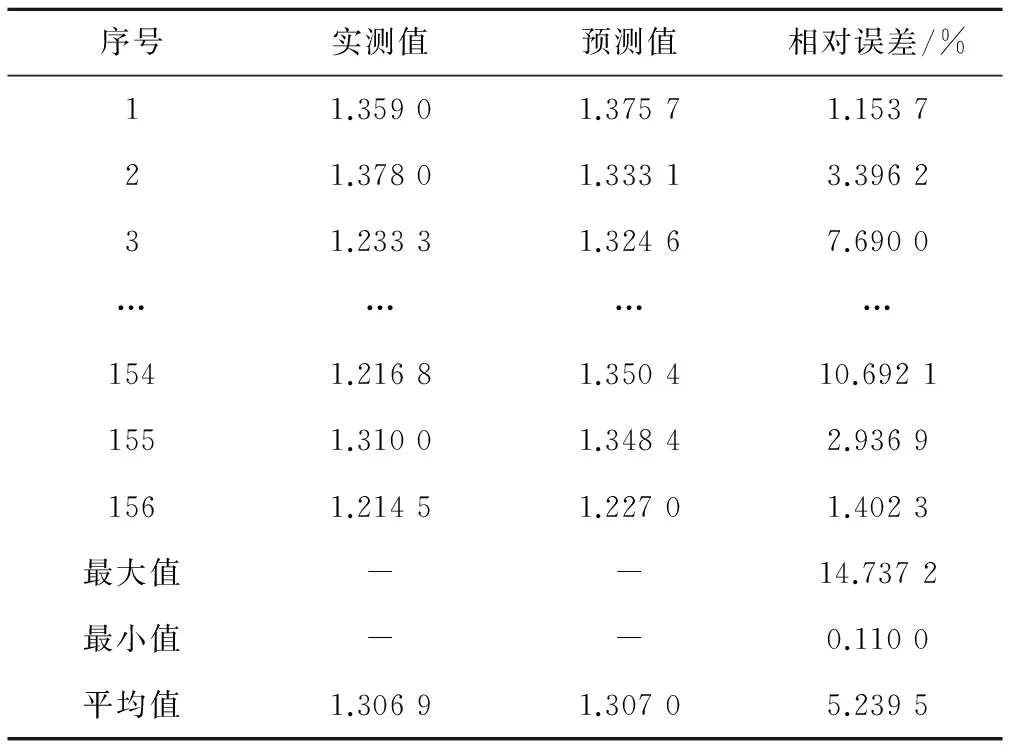
表7 建模樣本誤差分析表

從表7可以看出，地表土壤容重預(yù)測值與實測值的平均值相差無幾，說明整體預(yù)測效果較好；相對誤差平均值為5.24%，說明本文選定灰色關(guān)聯(lián)度較高的土壤黏粒含量、土壤粉粒含量、累積接收水量、體積含水率、有機質(zhì)含量和全鹽量6個影響土壤容重的參數(shù)作為輸入?yún)?shù)建立非線性預(yù)測模型是合理的，預(yù)測模型的精度很高。

3.2 驗證樣本的精度檢驗

為了檢驗?zāi)Ｐ偷念A(yù)測精度，采用隨機預(yù)留的8組數(shù)據(jù)，利用上述根據(jù)156組樣本建立的非線性預(yù)測模型對地表土壤容重進行預(yù)報，計算預(yù)測值與實測值的相對誤差和絕對誤差，計算結(jié)果如表8所示。

由隨機預(yù)留的8組數(shù)據(jù)的線性預(yù)報結(jié)果可知，地表土壤容重的預(yù)測值與實測值的平均值相差不大，相對誤差為1.43%～12.47%，綜合影響相對誤差的平均值為5.88%，預(yù)報精度完全在可接受范圍。這表明，利用本文所建的多元非線性模型可實現(xiàn)對地表土壤容重的預(yù)測，預(yù)報模型的整體精度較高，可滿足實際農(nóng)業(yè)生產(chǎn)活動需要，為獲取黃土高原區(qū)地表土壤容重參數(shù)提供依據(jù)。

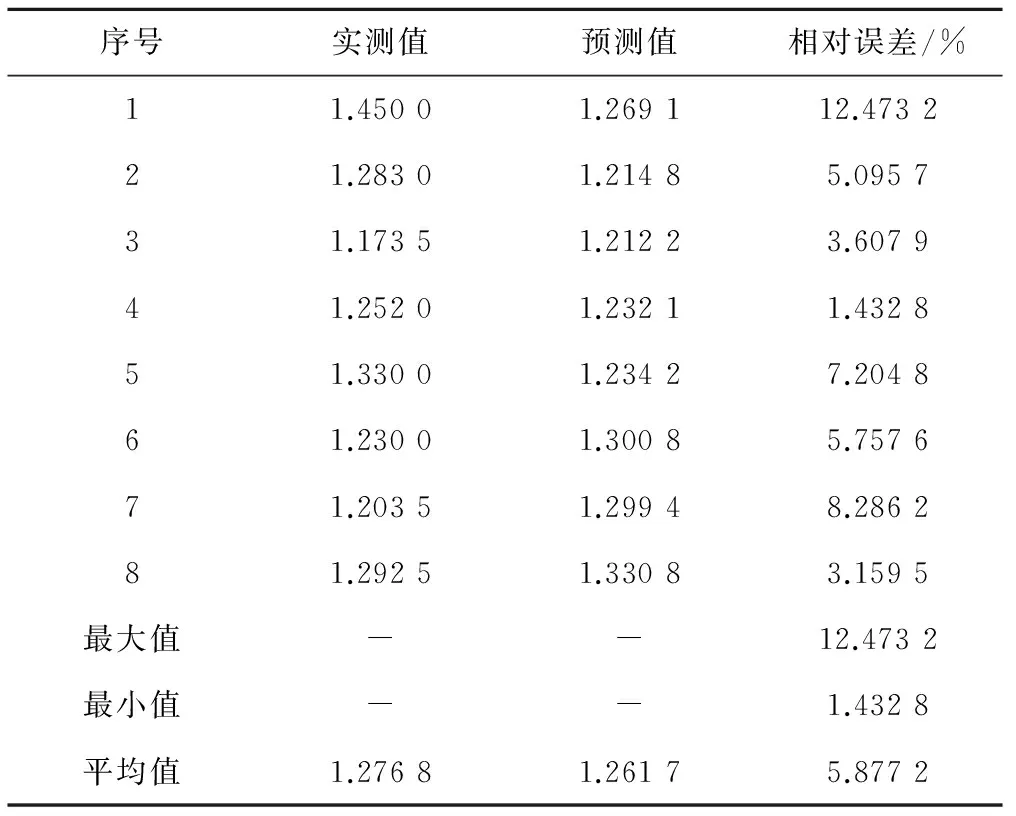
表8 驗證樣本的檢驗結(jié)果分析表

4 結(jié)論與建議

(1)地表(0～2 cm)土壤黏粒含量、粉粒含量、累積接收水量、有機質(zhì)含量、體積含水率和全鹽量可作為地表土壤容重預(yù)報模型的輸入變量。定性分析和模糊關(guān)聯(lián)度計算結(jié)果都表明：在黃土耕作農(nóng)田條件下，以上參數(shù)都是地表(0～2 cm)土壤容重的主要影響因素，各個影響因子的灰色關(guān)聯(lián)度均在0.7以上，關(guān)聯(lián)度很好。關(guān)聯(lián)度排序為黏粒含量>有機質(zhì)>累積接收水量>粉粒含量>體積含水率>砂粒含量>全鹽量。

(2)采取多元非線性回歸方法，以土壤黏粒含量、粉粒含量、累積接收水量、有機質(zhì)含量、體積含水率、和全鹽量為輸入變量對地表(0～2 cm)土壤容重預(yù)測是可行的。本文所建模型的顯著性檢驗值F值為28.50，遠大于F0.05，模型的顯著性較強；建模樣本和檢驗樣本相對誤差的平均值分別為5.24%和5.88%，預(yù)測精度高，實現(xiàn)了地表土壤容重的土壤傳輸函數(shù)預(yù)測，在一定程度上解決了獲取大面積農(nóng)田地表土壤容重野外工作難度大、成本投入高、隨機誤差大等問題。

由于數(shù)據(jù)樣本取自我國的黃土高原區(qū)，所建立的多元非線性預(yù)報模型有一定的地域適應(yīng)性，之后的研究可進行跨越多種土壤類型區(qū)域的更大建模樣本，提高其適用范圍和預(yù)測精度。

□

[1] 王 輝,王全九,邵明安.表層土壤容重對黃土坡面養(yǎng)分隨徑流遷移的影響[J].水土保持學(xué)報,2007,21(3):10-13.

[2] Kaur R, Kumar S, Gurung H P. A pedo-transfer function (PTF) for estimating soil bulk density from basic soil data and its comparison with existing PTFs[J].Australian Journal of Soil Research,2002,40(5):847-858.

[3] Bernoux M, Arrousys D, Cerri C, et al. Bulk densities of Brazilian Amazon soils related to other soil properties [J].Soil Sci.,1998,62(3):743-749.

[4] Omasella J, Hodnett M G. Estimating soil water retention haracteristics from limited data in Brazilian [J].Soil Science,1998,163(3):190-202.

[5] 程詩念,樊貴盛.玉米生育期內(nèi)不同覆膜對黃土表層容重變化特性的影響[J].節(jié)水灌溉,2017,(6):26-29.

[6] 張西超,鄒洪濤,張玉龍,等.灌溉方法對設(shè)施土壤理化性質(zhì)及番茄生長狀況的影響[J].水土保持學(xué)報,2015,29(6):143-147.

[7] 馮 棣,張俊鵬,孫池濤,等.長期咸水灌溉對土壤理化性質(zhì)和土壤酶活性的影響[J].水土保持學(xué)報,2014,28(3):171-176.

[8] Kaur R, Kumar S, Gurung H P. A pedo-transfer function (PTF) for estimating soil bulk density from basic soil data and its comparison with existing PTFs[J]. Australian Journal of Soil Research, 2002,40(5):847-858.

[9] 韓光中,王德彩,謝賢健.中國主要土壤類型的土壤容重傳遞函數(shù)研究[J].土壤學(xué)報,2016,53(1):93-102.

[10] 王巧利,林劍輝,許彥峰.基于BP神經(jīng)網(wǎng)絡(luò)的土壤容重預(yù)測模型[J].中國農(nóng)學(xué)通報,2014,30(24):237-245.

[11] 南京農(nóng)學(xué)院.土壤農(nóng)化分析[M]. 北京：農(nóng)業(yè)出版社,1980.

[12] 劉思峰,黨耀國,方志耕.灰色系統(tǒng)理論及其應(yīng)用[M].北京:科學(xué)出版社,2004.

[13] 劉思峰,蔡 華,楊英杰,等.灰色關(guān)聯(lián)分析模型研究進展[J].系統(tǒng)工程理論與實踐,2013,33(8):2 041-2 046.