SWMM模型參數全局敏感性分析

段明印，李傳奇，韓典乘，楊幸子

(山東大學土建與水利學院，山東 濟南 250061)

0 引 言

城市化的進程使得我國城市雨洪災害問題日益嚴峻，因此我國在防治雨洪災害的同時正在大力推行海綿城市的建設，暴雨管理模型(SWMM)可以模擬城市降雨地表徑流的產生和在排水管網中的輸送，能夠用來指導海綿城市的建設，因此在國內得到了較為廣泛的運用[1]。

準確率定SWMM的參數是精確構建SWMM模型、指導海綿城市建設的前提。但是SWMM參數較多，在率定時為提高效率可僅率定對輸出變量影響較為顯著的參數，那些對輸出變量影響較小的參數可直接取經驗值。因此，需要對SWMM參數進行敏感性分析，識別出影響較大的參數[2]。參數敏感性分析方法分為局部敏感性分析方法和全局敏感性分析方法，局部分析方法只是分析單個參數對輸出變量的影響，因其計算速度快，得到了較廣泛的運用，但是忽略了參數之間相互作用對輸出變量的影響，在“異參等效”的情況下會使一些敏感參數無法識別；全局分析方法可以分析參數之間相互作用對輸出變量的影響，能夠在“異參等效”的情況下識別出敏感參數，適用于參數眾多的模型[3]。

常見的全局敏感性分析方法有多元逐步回歸法[4]、Sobol法[5]、FAST法[6]、偏相關法、偏秩相關法等[3]。這些方法都是通過分析參數和輸出變量的線性相關關系來識別敏感參數，忽略了參數和輸出變量的非線性相關關系，可能導致某些敏感參數無法識別。因此，本文以某小區為例，選取能夠分析變量之間非線性關系的互信息法分析參數全局敏感性，將以互信息法分析的結果與能夠分析變量之間線性關系的偏秩相關法分析的結果相結合，精確識別所有敏感參數，為下一步高效率定打下基礎。

1 材料與方法

1.1 SWMM模型參數

在利用SWMM模型對興隆山校區進行降雨徑流模擬時，需要輸入的參數共計14個。這14個參數中的管渠長度和不透水面積可由設計資料讀取或者直接測量，所以僅對余下的12個參數的敏感性進行分析。其中子匯水區的面積、寬度、坡度這3個輸入參數具有顯著空間特性，輸入時存在測量誤差，所以定義3個修正系數：K-Area(面積修正系數)、K-With(寬度修正系數)和K-Slope(坡度修正系數)，確定這3個修正系數的分布范圍，則SWMM模型的輸入值為修正系數和對應參數的乘積[7]。依據SWMM使用手冊和國內相關文獻[7-11]確定參數的范圍，依據研究區域內的實測值確定參數初始值，參數分布及取值如表1所列。

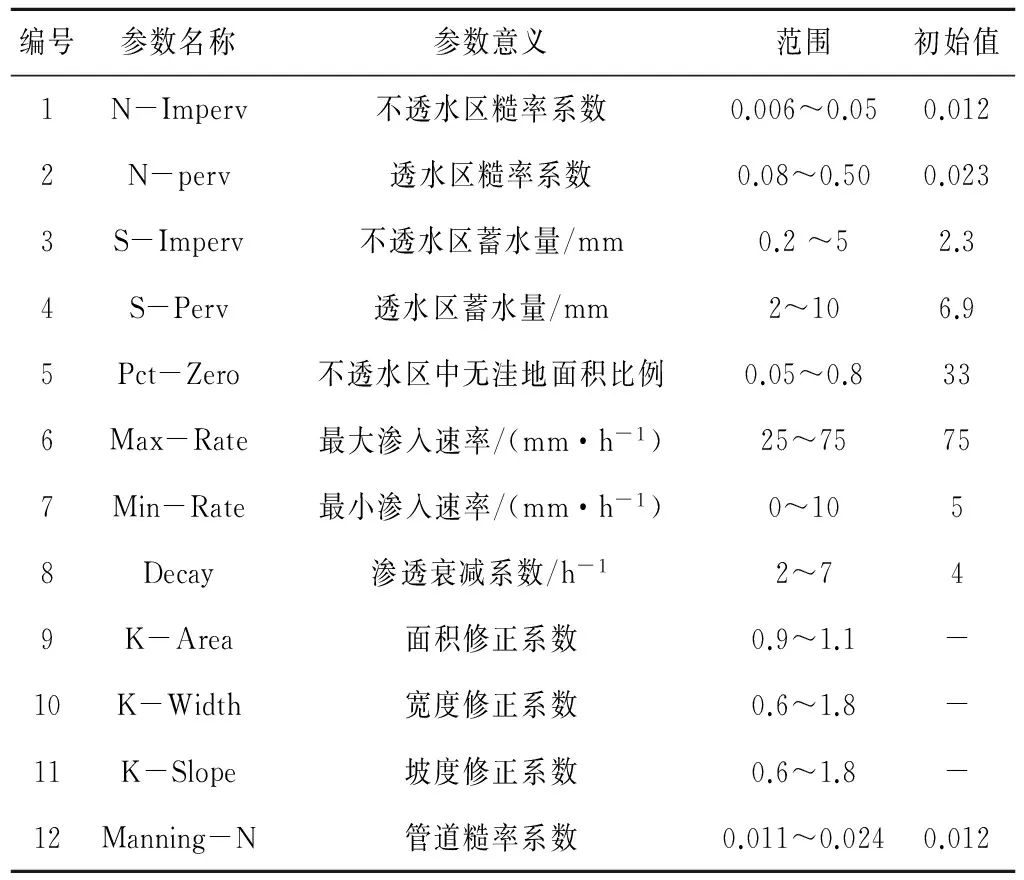
表1 SWMM參數取值表Tab.1 The parameters table of the storm water management model

1.2 SWMM模型構建

以山東大學興隆山校區為研究區域，該區總面積為63.82 萬m2，其中綠地面積較大，綠地面積高達30.82 萬m2，建筑占地面積為9.2 萬m2，道路占地面積8.9 萬m2，塊石鋪裝占地面積1.9 萬m2，硬質鋪裝面積8.7 萬m2，水體面積2.8 萬m2，足球場面積1.5 萬m2，研究區域概況如圖1所示。

圖1 研究區域概況Fig.1 The overview of study area

結合興隆山校區的地勢條件、地下管網資料、下墊面類型以及校區內的河道等資料，構建研究區的SWMM模型。SWMM模型包括45個子匯水區域，55個管道鉸點，55條雨水管道，3個排水口，興隆山SWMM模型如圖2所示。

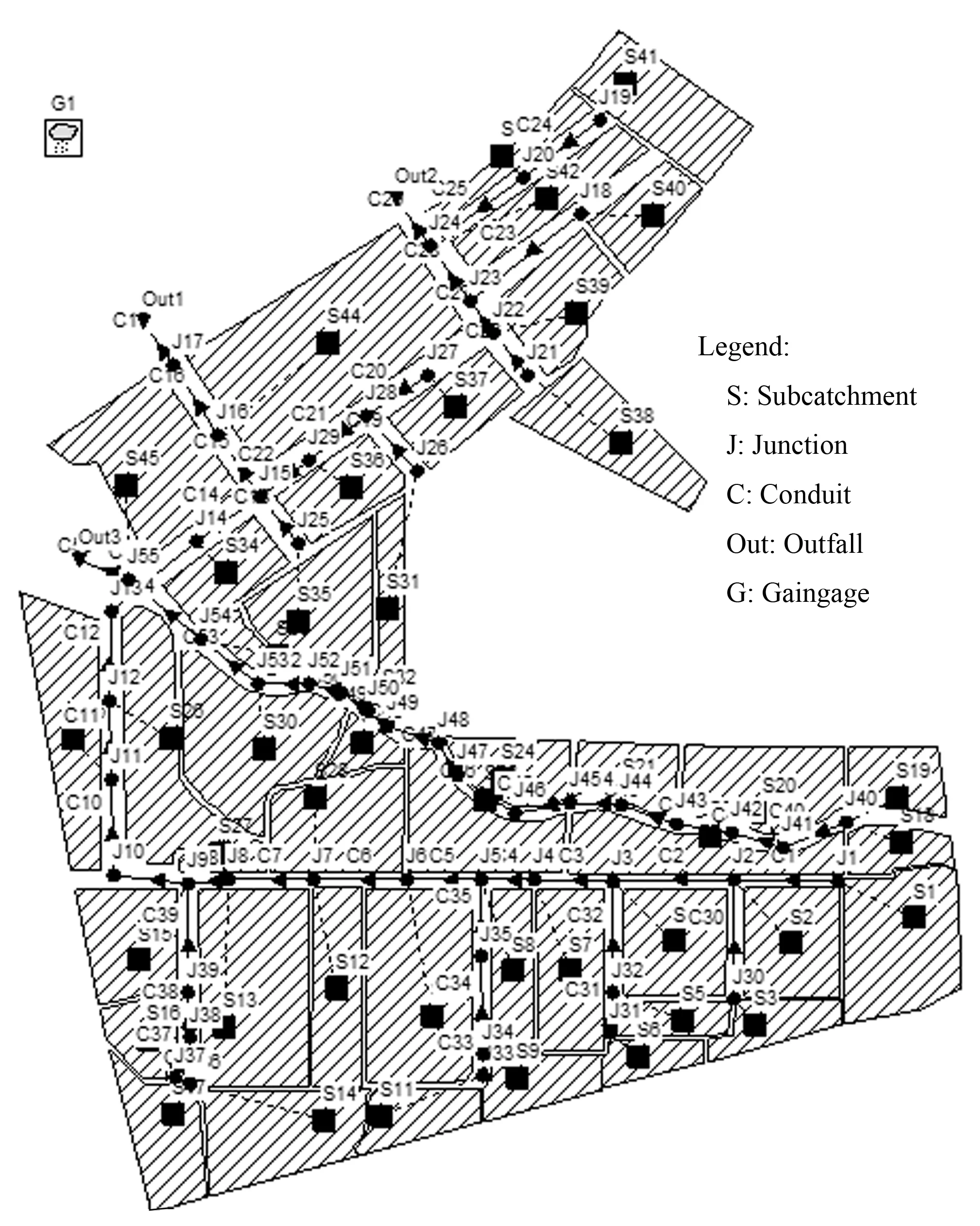
圖2 研究區域SWMM模型Fig.2 Storm water management model of the study area

1.3 抽樣方法

常見的抽樣方法有簡單隨機抽樣、分層抽樣和整群抽樣，分層抽樣方法的原理是將樣本空間分成互不交叉的若干層，然后從各層中抽取樣本，相對于簡單隨機抽樣和整群抽樣，分層抽樣能夠使得樣本點均勻地分布在樣本空間內，避免樣本集中的問題。因此本文選用拉丁超立方抽樣法在SWMM模型參數的分布空間內進行抽樣，拉丁超立方抽樣法屬于多維分層抽樣方法，能夠高效的抽取分布較為均勻的樣本[8]。

首先通過拉丁超立方抽樣法對有關降雨徑流的12個SWMM模型參數隨機抽樣1 000次，得到1 000組12個SWMM模型參數，然后通過MATLAB編程將這1 000組參數導入到SWMM模型的輸入文件中，生成1 000組新的SWMM輸入文件，利用SWMM模型將這1 000組輸入文件依次模擬，得到這1 000組參數對應的SWMM輸出文件，提取這1 000組輸出文件中某排放口的3個重要水文變量：流量峰值、流量峰值發生時間、總產流量，因為研究區域主要通過1號排放口排放總產流，因此提取1號排放口的3個水文變量作為3個因變量，以12個輸入參數作為自變量，分別以偏秩相關法和互信息法分析自變量和因變量之間的關系。

1.4 偏秩相關分析方法

偏秩相關分析是一種對變量分布不做要求的非參數統計分析方法，能夠對等級數據進行線性相關分析，在分析兩變量的相關關系時能夠控制其他變量的影響，因此能夠精確識別變量間的線性相關關系，可用做分析參數的全局敏感性[9]。

令輸出結果為Y，輸入參數為X1，X2，…，Xn，設這n+1個變量之間的Spearman秩相關系數r組成的矩陣為T，求矩陣T的逆矩陣得矩陣C。

(2)

則得某輸入參數Xi與輸出結果Y之間的偏秩相關系數PXi為：

(3)

式中：r為兩變量間Spearman秩相關系數；R2Xi為X1，X2,…,Xi-1,Xi+1,…,Xn線性回歸Xi的可決系數；RY2為它可決系數；Bi為X1，X2，…，Xn線性回歸Y的標準回歸系數；PXi為偏秩相關系數，它的絕對值大小為參數敏感性大小，它的正負表示呈正相關還是負相關。

1.5 互信息分析

互信息是指兩個變量之間或者多個變量之間共享的信息量，能夠度量變量之間的相關性，相關性越強，互信息越大。基于互信息的R統計量可以用來分析參數的全局敏感性，R統計量能夠精確識別參數和輸出結果之間的非線性相關關系，R統計量的大小代表參數的敏感性大小，但R統計量只能識別參數敏感性的大小，無法識別參數和輸出結果之間是正相關還是負相關[10]。

兩離散型隨機變量X與Y之間的互信息定義為：

(5)

R統計量表示為：

(6)

式中：p(x)為離散型隨機變量X取值x的概率；p(y)為離散型隨機變量Y取值y的概率；p(x,y)為X取值x、Y取值y同時發生的概率；I(x,y)為變量X、Y的互信息；b為互信息的量綱。本文互信息的量綱采用自然常數e，將SWMM模型的輸入參數視為離散型隨機變量X，將SWMM模型輸出結果視為離散型隨機變量Y，求解變量X與Y之間的互信息以及R統計量，分析參數對輸出結果影響的大小。在計算時為提高計算效率，將變量X分為i等份，將變量Y分為i等份，用pi表示變量X第i份中的數量占變量X總數量的概率，同時用pj表示變量Y第j份中的數量占變量Y總數量的概率，將分成i等份的變量X與分成j等份的Y組成聯立表，求得變量X和變量Y的聯合概率，用pij表示變量X在第i份取值、自變量Y在第j份取值同時發生的概率，則互信息的公式變為：

(7)

式中：i、j為輸入參數和輸出結果分成的等份數，本文都分為10等份；

1.6 降雨資料

降雨資料采用興隆山校區內雨量站(測站編碼：41822450)測得的降雨數據，選取20120708場次的降雨，該場次降雨歷時為13個小時，降雨量為47.5 mm，雨峰系數約為0.4，降雨強度過程如圖3所示。

2 結果與分析

2.1 初步分析

為初步分析SWMM模型的12參數和3個水文輸出結果的關系，分別畫出這1000組12個參數和3個輸出結果的殘差散點圖，其中散點圖的橫坐標為某一參數與控制參數回歸分析得到的殘差，縱坐標為輸出結果與控制參數回歸分析得到的殘差。各個參數和峰值流量的關系如圖4所示，觀察發現Manning-N與峰值流量的殘差散點圖幾乎在一條一直線上，具有高度的線性關系，呈負相關。各個參數和峰值時間的關系如圖5所示，觀察發現N-perv和峰值時間具有較強的線性關系，呈負 相關。各個參數和總產流量的關系如圖6所示，觀察發現Manning-N、Min-Rate和總徑流量具有較強的負相關關系，其中Manning-N和總產流量的負相關性強于Min-Rate。

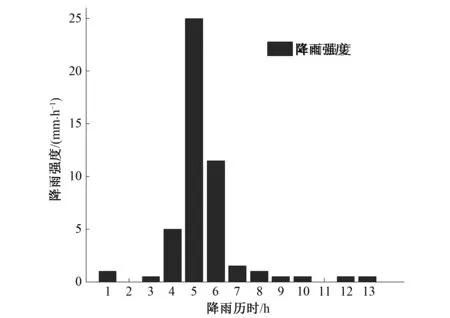
圖3 研究區域20120708場次降雨強度過程Fig.3 Rainfall intensity processes of label 20120708 in the study area

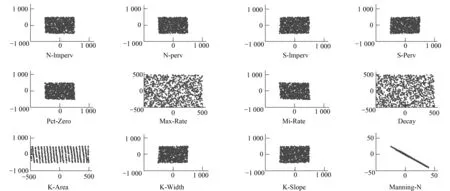
圖4 參數和峰值流量殘差散點圖Fig.4 Residual scatter diagram of parameters and peak flow

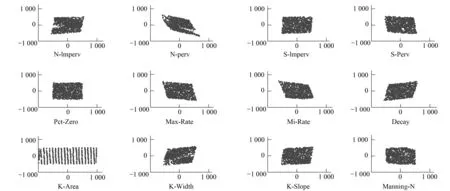
圖5 參數和峰值時間殘差散點圖Fig.5 Residual scatter diagram of parameters and peak time

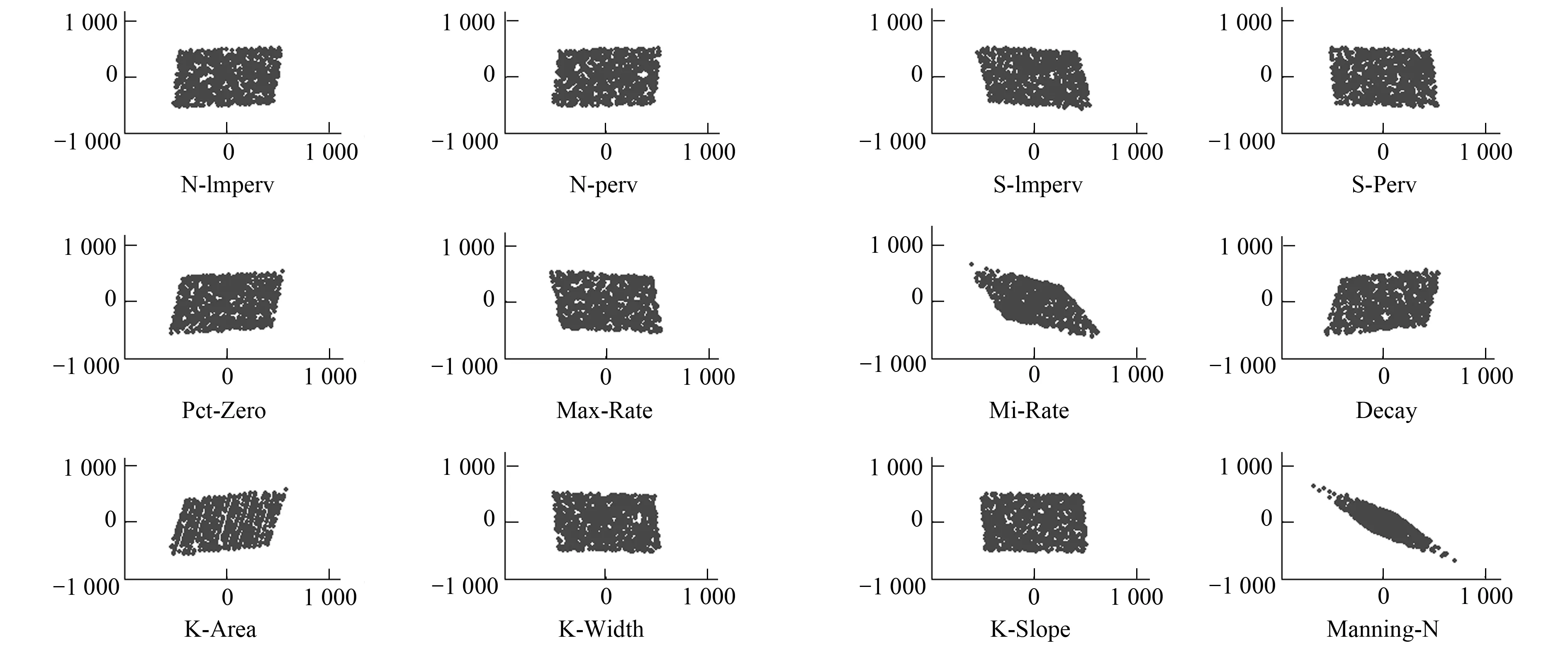
圖6 參數和總產流量殘差散點圖Fig.6 Residual scatter diagram of parameters and total runoff volume

2.2 偏秩相關分析

通過MATLAB編程利用偏秩相關分析方法分析參數和輸出結果的相關性，分析結果如表2所列。由表2可以得出參數和輸出結果之間線性相關關系的強弱，即參數的敏感性大小。對峰值流量來說，最敏感的參數是Manning-N，它與峰值流量的偏秩相關系數P高達-0.996，具有高度的線性關系；第二敏感參數是N-perv，P值的絕對值位0.670，排名前兩位的敏感參數和峰值流量都是負相關關系，這是因為管渠和透水地表的糙率系數增大會使滯蓄雨水量增大，從而使得峰值流量減小；其他參數的敏感性相對較小，說明Manning-N和N-perv對峰值流量起著決定性作用。對峰值時間來說，最敏感的參數是N-perv，P值為-0.417，呈負相關，其他參數的敏感性都較小。對總產流量來說，最敏感的參數是Manning-N，P值高達-0.936，具有高度的線性關系，第二敏感參數是Min-Rate，P值為-0.838，其與總產流量也具有較強的線性關系；Manning-N、Min-Rate與總產流量都是負相關關系，Manning-N和Min-Rate的增大將會使總產流量減小，這是因為最小滲透率增加將會使雨水下滲量增大，管渠糙率增大會使管渠滯蓄雨水量增大，這些都會使總產流量減小。

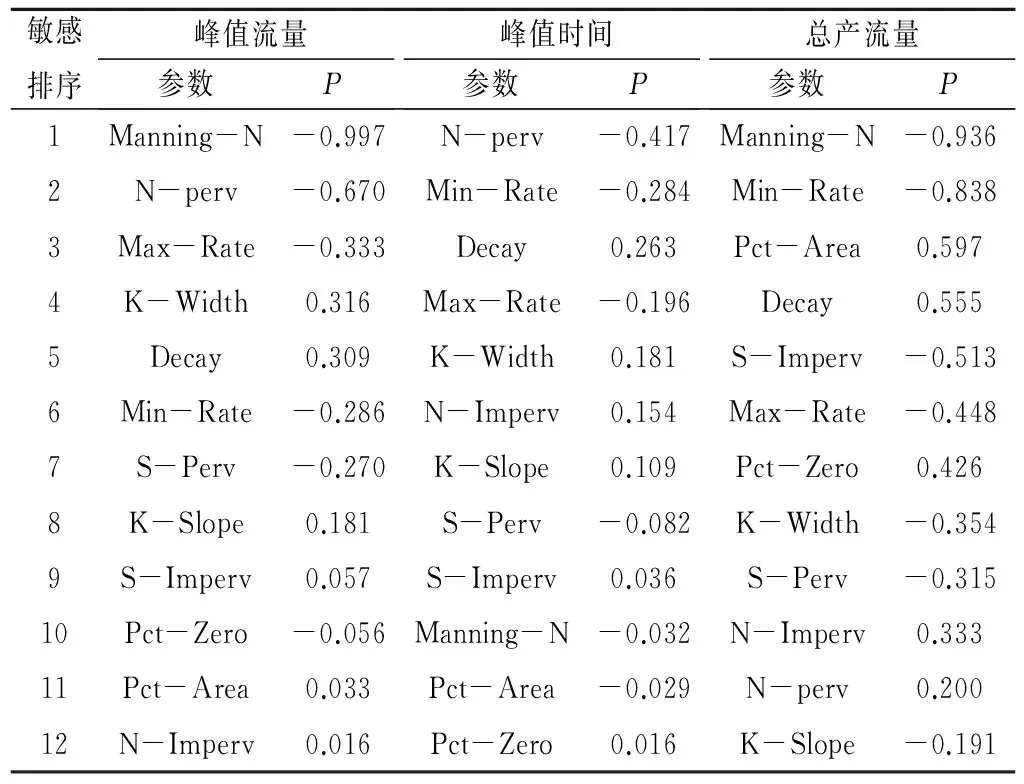
表2 偏秩相關分析結果Tab.2 Result of partial rank correlation analysis

2.3 互信息分析

通過MATLAB編程利用互信息相關原理分析參數和輸出結果之間的非線性相關關系，結果如表3所列。根據表3中的R統計值可以判斷參數和輸出結果之間非線性關系的強弱，及參數敏感性的大小。對峰值流量來說，最敏感的參數是Manning-N，R值高達0.886，這說明Manning-N和峰值流量之間具有較強的非線性相關關系；其他參數的R值較小，說明其他參數和峰值流量的非線性關系較弱。對峰值時間來說，N-perv是最敏感的參數，R值為0.457，說明N-perv和峰值時間的非線性關系較弱；第二敏感參數是K-Width，R值僅為0.337，對峰值時間影響較小，其他參數對峰值時間的影響也都較小。對總產流量來說，Manning-N是最敏感的參數，R值為0.574；第二敏感參數是Min-Rate，R值僅為0.372，說明其對總產流量的影響較小。

將偏秩相關分析的結果和互信息分析的結果進行對比發現：兩種方法所求的對峰值流量最敏感的參數都是Manning-N，但是用偏秩相關法算出的敏感性大小為0.997，大于用互信息法算出的敏感性大小，說明Manning-N和峰值流量的線性關系強于非線性關系；對峰值時間而言，兩種方法求得的最敏感參數都是N-perv，但是互信息求得的R值大于偏秩相關法求得的P值絕對值，說明N-perv與峰值時間的非線性關系強于線性關系；對總產流量來說，兩種方法求得的最敏感參數都是Manning-N，且偏秩相關法求得的P值絕對值大于互信息法求得的R值，說明Manning-N和總產流量的線性關系強于非線性關系；兩種方法識別出的較敏感參數存在差異，這是因為偏秩相關法是通過分析線性相關關系來識別敏感參數，互信息法是通過分析非線性相關關系來識別敏感參數，因此二者識別的敏感參數存在差異，但是這兩種方法可以共同使用，從而全面識別敏感參數，避免只用一種方法而導致的疏漏。

3 結 語

(1)偏秩相關分析方法能夠通過分析參數和輸出結果之間的線性關系來識別敏感參數，互信息法能夠通過分析參數和輸出結果之間的非線性關系來識別敏感參數，這兩種方法都是全局敏感新分析方法，將兩種方法結合使用能夠精確識別所有的敏感參數。

(2)通過兩種分析方法得知，Manning-N是對峰值流量影響最大的參數，Manning-N的增大將會使峰值流量減小；N-perv是對峰值時間影響最大的參數，N-perv的增大將會使峰值時間提前；Manning-N是對總產流量影響最大的參數，Manning-N的增大將會使總產流量減小。

(3)通過敏感性分析，精確識別所有敏感參數，能夠在率定過程中提高效率。

□

[1] 官奕宏,呂 謀,王 燦,等. 低影響開發技術的雨洪控制效果及水質影響分析——基于SWMM模型[J]. 中國農村水利水電,2017,411(1):84-87.

[2] 朱嘉祺,徐向陽,何 爽. 基于LH-OAT的SWMM模型參數敏感性分析[J]. 中國農村水利水電,2014,377(3):21-26.

[3] 宋曉猛,張建云,占車生,等. 水文模型參數敏感性分析方法評述[J]. 水利水電科技進展,2015,35(6):105-112.

[4] ZHOU N, PIERRE J W, TRUDNOWSKI D. A stepwise regression method for estimating dominant electromechanical modes[J]. IEEE Transactions on power systems. 2012,27(2):1 051-1 059.

[5] 王海霞,李 昱,周惠成,等. 基于Sobol’敏感性分析法的水庫多目標調度模型求解質量與效率[J]. 水電能源科學,2016,34(6):43-47.

[6] 任啟偉,陳洋波,舒曉娟. 基于Extend FAST方法的新安江模型參數全局敏感性分析[J]. 中山大學學報(自然科學版),2010,49(3):127-134.

[7] 王浩昌,杜鵬飛,趙冬泉,等. 城市降雨徑流模型參數全局靈敏度分析[J]. 中國環境科學,2008,28(8):725-729.

[8] Chen Y, Wen J, Cheng S. Probabilistic load flow method based on nataf transformation and latin hypercube sampling[J]. IEEE Transactions on sustainable energy, 2013,4(2):294-301.

[9] 曹 淵,韓 峰,王鐵良,等. 爆炸容器力學安全的敏感度分析方法[J]. 科技導報,2013,31(3):28-32.

[10] 熊劍智. 城市雨洪模型參數敏感性分析與率定[D]. 濟南:山東大學,2016.

[11] 侯改娟. 綠色建筑與小區低影響開發雨水系統模型研究[D]. 重慶:重慶大學,2014.