水分特征曲線Gardner模型參數的預測模型對比分析

李浩然，樊貴盛

(太原理工大學水利科學與工程學院，太原 030024)

土壤水分特征曲線是描述土壤基質勢與土壤含水量之間關系的基本曲線[1]，可以反映出土壤孔隙結構特點與持水能力，對于研究土壤水分動態、溶質運移等有著重要的意義。在對土壤水分特征曲線的研究中，許多學者提出了不同的物理—經驗模型用來對土壤水分特征曲線進行描述。目前，常見的經驗模型有V-G模型、Gardner模型、F-X模型等，其中Gardner模型由于其簡單的結構形式、少量的參數以及較高的精確性等優點，受到眾多學者的認同。宋孝玉等[2]通過部分不同區域土壤進行了Gardner模型建立與比較，證明了Gardner模型的準確性與適用性；張露[3]等利用Gardner模型成功擬合出不同復配土壤的土壤水分特征曲線；李逸[4]等利用Gardner模型進行擬合，得出了土壤水分特征曲線的斜率主要由土壤質地決定的結論等。

而在土壤水分特征曲線的研究中，如何準確地獲取模型中的參數一直是人們研究的重點。對于模型參數的獲取一般有直接法(負壓計法、壓力膜儀法、砂形漏斗法)與間接法。由于直接方法在對參數的測定中需要耗費較多的人力物力，同時測量的結果易受外界條件的影響，從而導致精度較差。目前，隨著土壤傳輸理論的發展，運用土壤傳輸函數對土壤特征參數進行預測的間接方法成為了人們研究的焦點。李曉鵬等[5]使用多種不同的土壤傳輸函數，對不同地區土壤的飽和含水率進行了預測，并成功得出適合各地區飽和含水率的飽和含水率；舒凱民[6]等利用BP神經網絡對入滲參數進行預測，并取得了較好的效果；Vereecken[7]運用線性回歸分析對土壤水分特征曲線參數進行了研究，即對模型參數進行了線性函數的預測。

根據以上研究可以看出，土壤傳輸函數可以有效地對土壤的特征參數與運動參數進行推求與預測。但是，對于土壤水分特征曲線Gardner模型參數的研究還鮮有報道。目前，在土壤傳輸函數的方法中，BP人工神經網絡與支持向量機(SVM)是運用相對廣泛、精度較高的兩種方法。因此，本研究將在不同輸入變量的條件下，利用BP神經網絡與支持向量機兩種預測手段對Gardner模型參數進行預測，并對預測模型的精度進行分析，為土壤水分特征曲線Gardner模型參數的預報模型的創建提供依據和參考。

1 材料與方法

1.1 試驗區土壤條件

試驗所用土樣均來自山西省中西部地區的耕作農田。試驗區地貌條件為平原、丘陵和高原等，氣候屬于典型的溫帶大陸性氣候。土壤類型有黃褐土、棕壤土等；土壤質地類型復雜多樣，主要包括粉砂質壤土、砂質壤土等。試驗區土壤基本理化參數變化范圍如表1所示。

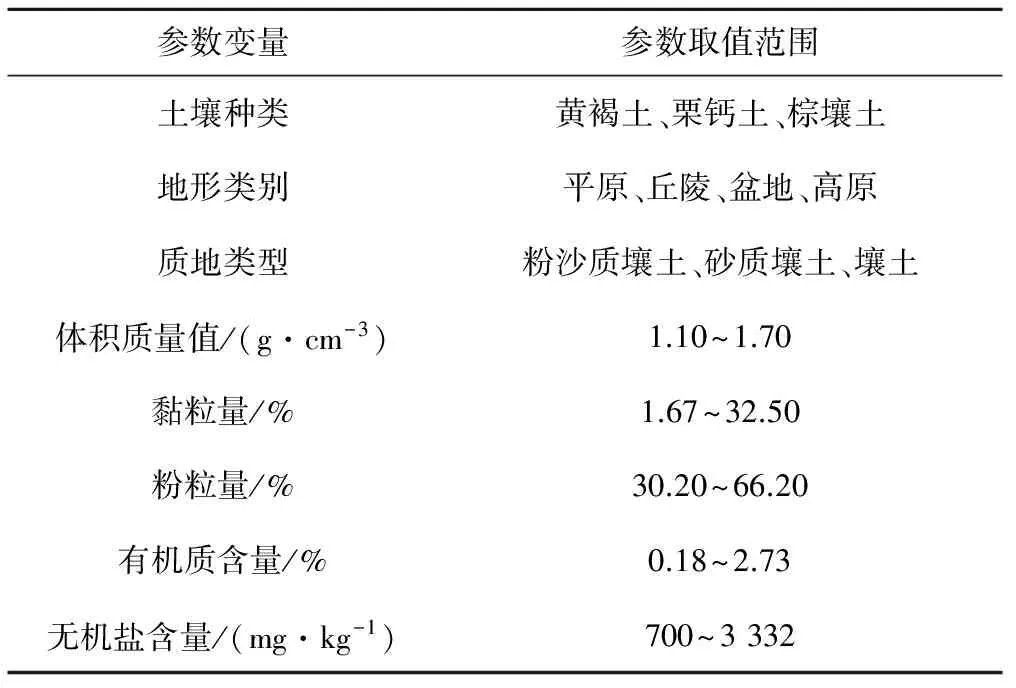
表1 土壤樣本數據的取值范圍

1.2 試驗設備與方法

本文土壤水分特征曲線試驗使用1500F壓力膜儀進行。首先將土樣風干、過篩，并將其裝入相應的環刀內，然后將環刀放入儀器中的陶土板中令其吸水以保證土樣達到水分飽和。當土樣達到水分飽和后，對土樣進行固定壓力值的施壓，以保證土壤中的水分可以充分排出，并間隔固定時間對土樣進行稱重。當前后稱重的土樣重量變化小于0.005 g，則認為土樣中的水分全部排出，開始進行下一壓力值的試驗。最后計算含水率，并通過相應的計算擬合得到Gardner模型參數值。

本次試驗需要測定的土壤基本理化參數主要包括土壤容重、土壤質地、有機質含量、無機鹽含量。其中由于是土樣為擾動圖，土樣容重按照1.10～1.70 g/cm3進行配置；土壤質地通過激光粒度分析儀對土壤中的黏粒、砂粒、粉粒含量進行測定；土壤有機質含量使用重鉻酸鉀容量法測定；土壤無機鹽含量是通過火焰光度計等儀器對八大離子進行測定，并將測定值累加，和值為無機鹽含量。

1.3 Gardner模型

Gardner模型是Gardner在1970年提出[8,9]，因其結構簡單、精度及較高而廣泛應用于實際當中。 Gardner模型的具體表達式為：

h=aθ-b

(1)

式中：h為土壤水吸力，cm；θ為土壤體積含水率，%；a、b均為擬合參數，無單位量綱且均為正數。

1.4 數據樣本

通過實驗，建立了100組數據的樣本，即建立了土壤基本理化參數與Gardner模型參數a、b的一一對應關系，代表性數據樣本見表2。

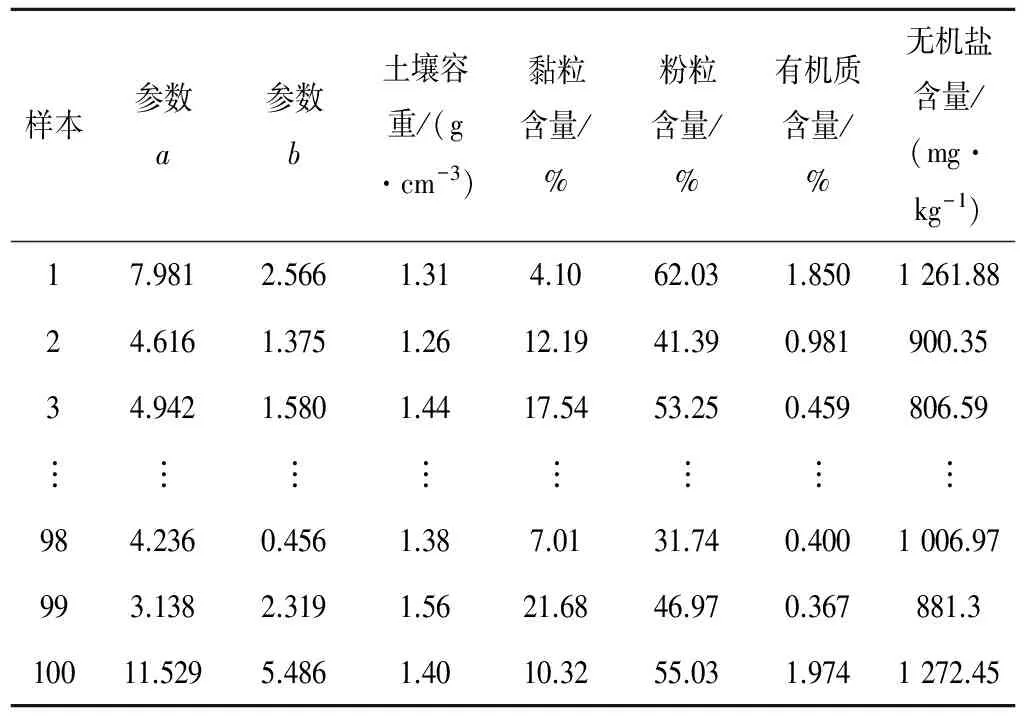
表2 建模樣本數據表

2 輸入變量情景設計與預測模型的建立

2.1 土壤水分特征曲線主導因素分析

土壤水分特征曲線的過程線決定著Gardner模型的參數，而影響土壤持水性能的土壤基本理化參數的較多。前人[10,11]和本文的分析認為主要的影響因子有土壤質地、土壤容重、土壤有機質含量、土壤無機鹽含量等。

(1)土壤質地。土壤質地主要是指土壤中黏粒、粉粒、砂粒的組成情況。對于土壤而言，如果土壤中的黏粒含量與粉粒含量越高，土壤中會形成較多的中小空隙，進而導致土壤中的毛管吸力增大，使得土壤的持水性能增加；另一方面，中小孔隙的增加會增加土壤的比表面積，表面能變大，從而導致土壤顆粒對水分的吸附能力變強。

(2)土壤容重。土壤容重表示的是土壤結構的密實程度與板結程度。對于多孔隙的土壤而言，土壤容重的增大代表著土壤被壓縮破壞，土壤中的大孔隙被擠壓破壞形成中小孔隙，從而導致土壤的毛管吸力與土體顆粒對水分的吸附能力變強。

(3)土壤有機質含量。土壤中的有機質主要是指土壤內的膠結物質，這些物質會增大土壤的黏性從而改變土壤的內部結構。在有機質的作用下，土壤內的中小孔隙的結構變得比較穩定，因此有著較強的持水穩定性。

(4)土壤無機鹽含量。土壤中的無機鹽含量主要是指土壤中的八大離子的含量總和，隨著土壤中的含鹽量的增加，土壤分散度變大，土壤中的大孔隙崩塌，從而形成較多的中小孔隙，從而加強土壤的持水性能。

2.2 輸入變量情景設計

為了探究輸入變量對于BP神經網絡與支持向量機預報模型預測精度的影響，需要對輸入變量的選擇方面設計了不同的情景模式。

輸入變量的情景設計主要以輸入變量的數量和類型為原則。根據查閱文獻與機理分析，認為土壤持水能力與土壤質地與土壤容重有著直接的關系，因此在設計輸入變量的時候，土壤質地與土壤容重是不可或缺的變量；同時，還應考慮到土壤有機質含量與土壤無機鹽含量對土壤持水性能的作用，以及輸入變量數量的改變對Gardner模型參數預測精度的影響。

將以上因素綜合考慮，最終確定的輸入變量情景為3種模式，分別為：①土壤質地+土壤容重；②土壤質地+土壤容重+土壤有機質含量；③土壤質地+土壤容重+土壤有機質含量+土壤無機鹽含量。

2.3 土壤傳輸函數預報模型

(1)支持向量機是Corinna Cortes和Vapnik等于1995年首先提出的一種處理小數據、非線性等問題的機器學習方法。支持向量機通過特定的映射，將因變量投影到高緯度的運算空間當中，借助于核函數展開計算，從而解決樣本空間的非線性分類與回歸分析的問題。支持向量機由于能有效避免預測過程中的“過學習”、“過擬合”等問題，因此在近些年受到廣大學者的關注研究。具體預測模型如下：

model=svmstrain(train_Y,train_X, ‘options’)

(2)

式中：svmtrain為向量機訓練形式；train_X為自變量訓練集屬性矩陣，包括輸入變量；train_Y為因變量訓練集標簽，包括Gardner模型參數；options為參數選項，依據核函數類型，主要包括C、ε、σ，其中，C為懲罰因子；ε為不敏感損失函數值；σ為核函數參數。式(2)為支持向量機模型。

(2)BP神經網絡是1986年由Rumelhart和McClelland提出的一種按照誤差逆向傳播算法訓練的多層前饋神經網絡。BP神經網絡因其自身特有的對于非線性關系處理能力與相對簡單的組成結構，在眾多人工神經網絡中研究最為成熟，是目前應用最廣泛的神經網絡。具體預測模型如下：

net=newff( min max(traininput),[20,2],{‘tan sig’,‘purelin’},‘trainlm’)

(3)

式中：net為本文所創建的BP神經網絡模型；newff為在Matlab程序中的BP神經網絡函數；min max( ) 為決定輸入參數取值范圍的向量矩陣；20和2為分別為隱含層和輸出層神經元的個數；{‘tan sig’,‘purelin’}分別為隱含層和輸出層的傳輸函數形式；‘trainlm’ 為訓練函數形式。式(3)為BP網絡模型。

2.4 預報模參數與成果

2.4.1 樣本數據預處理

為了方便預報模型的計算以及減少輸入因素量綱對預測精度的影響，因此對輸入變量的數據進行歸一化處理，歸一化處理公式如下。

(4)

式中：Y為歸一化處理后的數據；X為樣本數據；Xmin、Xmax分別為樣本數據的最大值與最小值。

2.4.2 BP模型結構與相關參數

(1)BP神經網絡的結構主要分為輸入層、隱含層、輸出層。通過對樣本不停地學習與訓練，以均方誤差最小化作為反饋結果，進而修正調整網絡權值和閾值，最終高度擬合數據并得出結果。BP神經網絡結構如圖1所示。

圖1 BP神經網絡結構圖

(2)BP相關參數。本文所用BP神經網絡預報模型的參數設定為最大學習迭代次數為1 500次，學習率0.01，訓練精度為0.000 5。最終確定的參數如表3所示。

2.4.3 SVM模型相關參數

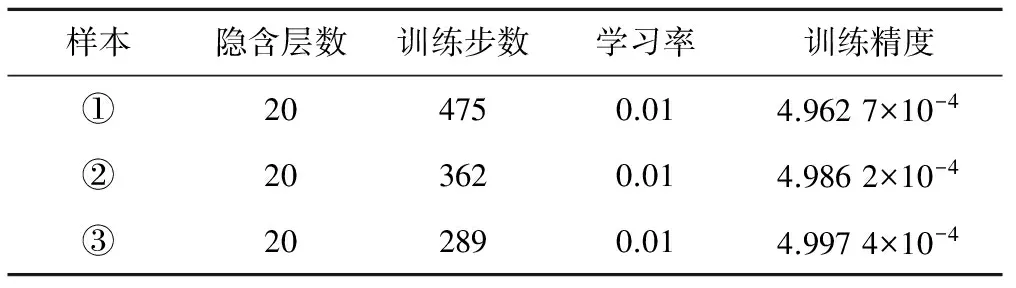
表3 BP神經網絡預報模型參數

(1)SVM結構。支持向量機是將輸入變量映射到高維空間中，在高維空間中尋找一個最優分類超平面，保證訓練樣本中不同分屬的點可以很好地分布在超平面的不同側面，從而使空白區域實現最大化，同時此超平面即為支持向量機的結果。支持向量機結構如圖2所示。

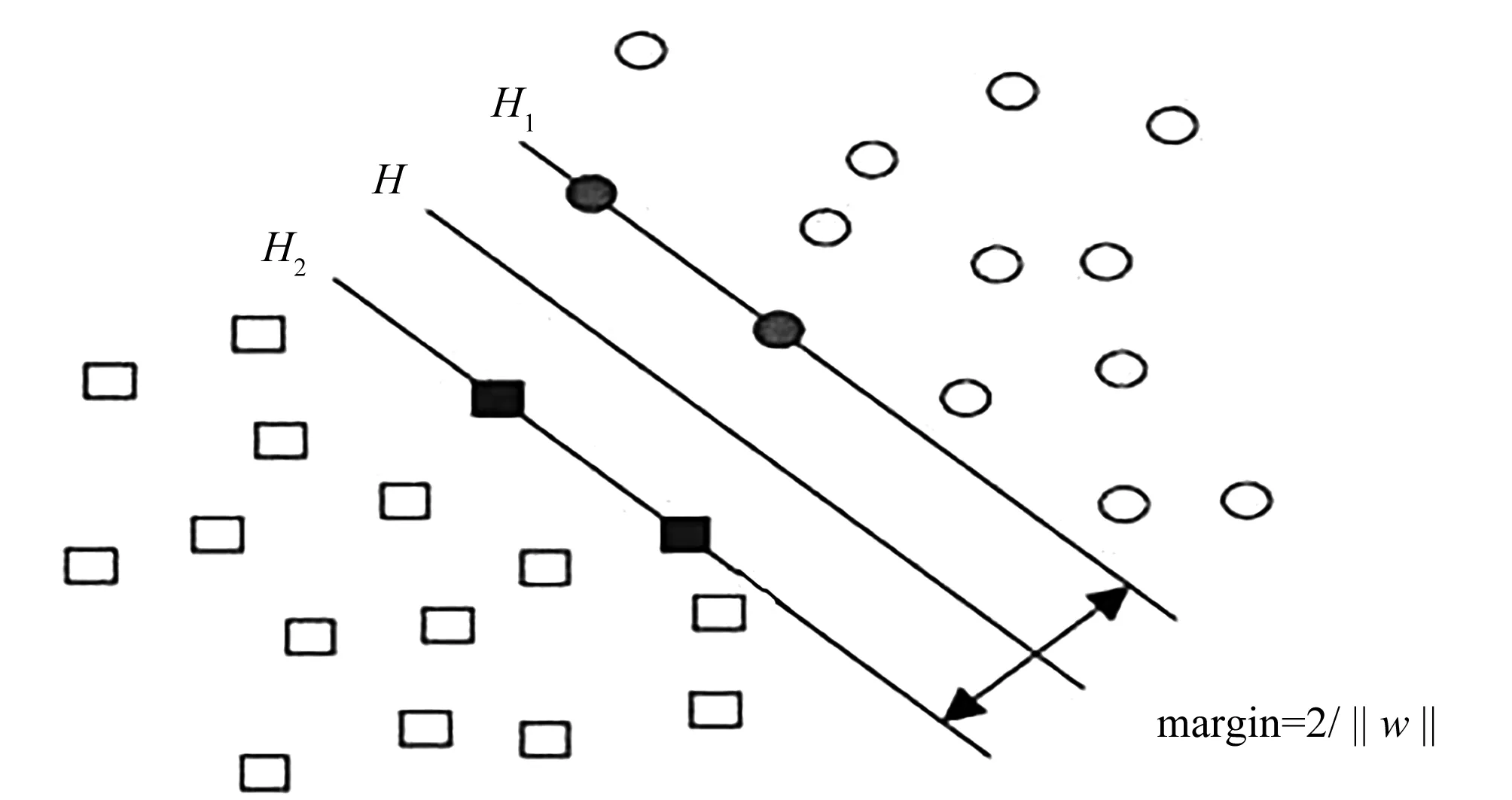
圖2 SVM最優超平面示意圖

(2)SVM相關參數。本文所用支持向量機預報模型的相關參數主要有C、σ、ε，其中C為懲罰因子，ε為不敏感損失函數值，σ為核函數參數。最終確定的參數如表4所示。

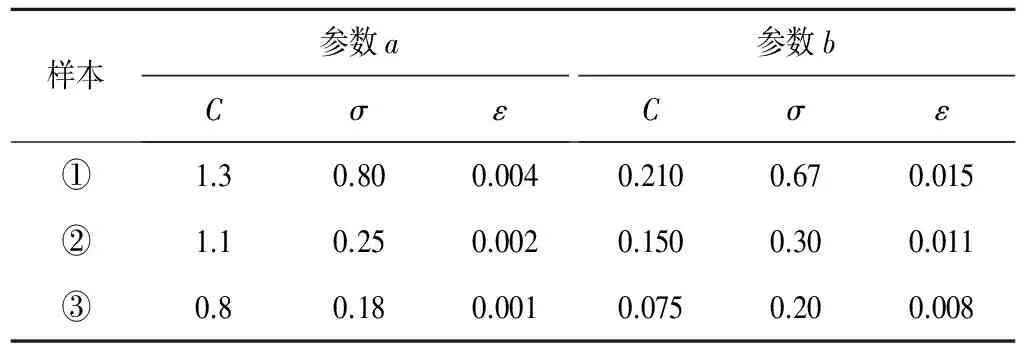
表4 SVM預報模型參數

3 預報模型精度比較

將歸一化處理后的樣本數據按分別通過支持向量機與BP神經網絡的預報模型的預測，并將預測值與實測值進行比較。預測結果的精度比較如表5所示。

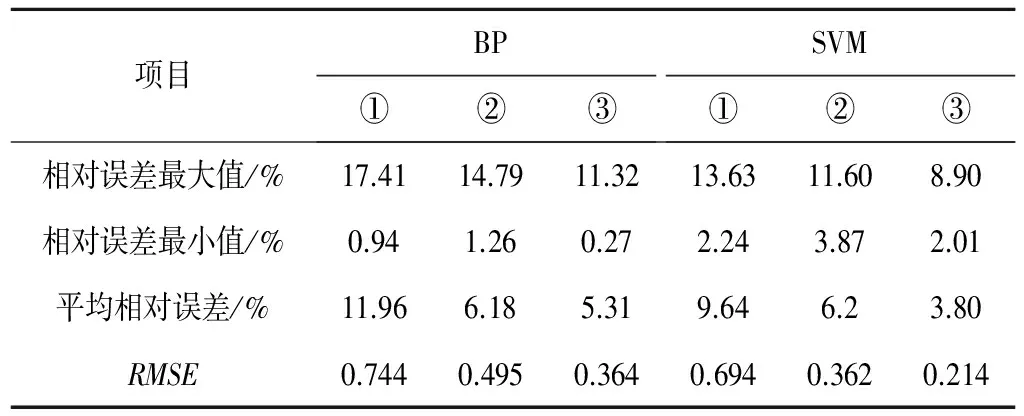
表5 參數a預測誤差結果表

注：RMSE為均方根誤差。

由表5可知，當輸入變量只有土壤質地與土壤容重時，兩種模型的平均相對誤差分別為11.96%與9.64%，相對誤差較大，精度較低；但是隨著輸入變量種類的增加，無論是BP神經網絡預報模型模型還是支持向量機預報模型，對于參數a預測的相對誤差值呈現出逐漸下降的趨勢，模型的預測精度不斷提高，并在輸入變量為土壤質地、土壤容重、土壤有機質含量、土壤無機鹽含量時，平均相對誤差達到最小值，分別為5.31%與3.80%，預測精度較好。這不僅說明輸入因子的種類變化對Gardner模型參數的預測精度的影響程度較為明顯，同時證明了兩種預測模型可以實現對于Gardner模型參數a的預測。

將兩個預報模型進行對比，兩者的誤差相差較小，精度相似。隨著輸入變量的增加，BP神經網絡的相對誤差最大值分別為17.41%、14.79%、11.32%，最小值分別為0.94%、1.26%、0.27%；支持向量機的相對誤差最大值分別為13.63%、11.6%、8.9%，最小值為2.24%、3.87%、2.01%。可以看出，雖然BP神經網絡的最小相對誤差值比支持向量機要小，但是就相對誤差波動的范圍而言，支持向量機的預測結果的波動程度較低，變化幅度較小；另一方面，RMSE是一種反映預測值與實測值之間偏差程度的數學手段，RMSE越小則實測值與預測值之間的離散程度越小，從表5可以看出，無論輸入變量的種類有多少，支持向量機對于參數a的RMSE都比BP神經網絡小，從而進一步說明支持向量機的預測結果的相對穩定，能夠有效的保證預測結果的精度。

如表6所示，與參數a的預測結果相似，無論是BP神經網絡還是支持向量機，預測精度均會隨著輸入變量的增加而提高，最終平均相對誤差分別為5.56%與3.76%，預測精度較高，說明了土壤基本理化參數的變化對預測的效果有著明顯的影響。而且將兩種模型進行對比，BP神經網絡預測誤差的最大值為19.04%、13.79%、10.58%，最小值為1.07%、0.627%、0.651%；支持向量機預測誤差最大值為16.86%、12.56%、7.86%，最小值為3.21%、2.16%、1.27%。同參數a的結果相似，雖然BP神經網絡的最小相對誤差值比支持向量機的要小，但是支持向量機預測的相對誤差區間相對較小，同時根據RMSE的數值可以看出支持向量機對于參數b的預測結果的離散程度較低，吻合度相對較高。

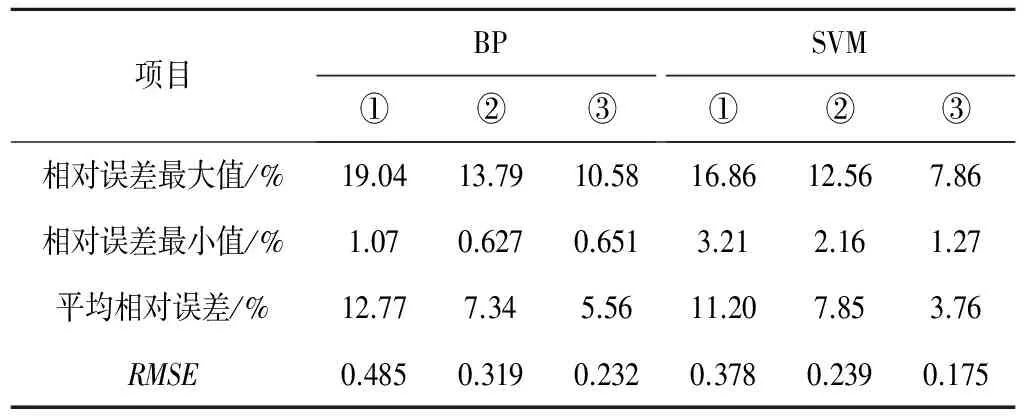
表6 參數b預測誤差結果表

綜上所述，對于Gardner模型而言，改變輸入因子的類型與數量可以有效地提高預測的精度，并且能夠有效的對Gardner模型參數進行有效的預測。同時，采用支持向量機算法對Gardner模型參數進行預測，所得到的結果相對穩定，吻合度較好，使得相對誤差保持在較小的范圍內，相比于BP神經網絡的波動性，支持向量機能夠使預測結果保持較好的穩定性。

4 結 語

(1)在土壤特征曲線主要影響因素范圍內，兩種預報模型的預報精度隨著輸入因子類型的增加而提高，并在輸入變量為土壤質地、土壤容重、土壤有機質含量、土壤無機鹽含量時精度達到最高，預測結果的平均相對誤差均在6%以下。以土壤質地、容重、有機質含量、無機鹽含量為輸入變量的BP神經網絡與支持向量機預報模型都可用于Gardner模型參數的預測。

(2)BP神經網絡預報模型的預測誤差的最小值小于支持向量機的最小值，但是支持向量機預報模型預測結果的波動較小，RMSE較低，預測結果吻合度較高，支持向量機預報模型相對于BP神經網絡模型有著更好的穩定性準確性。

(3)本文研究了BP神經網絡與支持向量機預報模型的預測結果，證明了支持向量機對于Gardner模型參數的預測有著更高的精確度。此次研究為土壤水分特征曲線參數預測方法的選擇提供了理論依據。在今后的實驗中，會嘗試不同的預測方法，比如灰色預測模型、BNN預測模型等，對Gardner模型參數進行預測以及對比分析，進一步豐富土壤傳輸函數理論。

[1] 雷志棟，楊詩秀，謝傳森.土壤水動力學[M].北京：清華大學出版社，1988．

[2] 宋孝玉, 李亞娟, 李懷有,等. 土壤水分特征曲線單一參數模型的建立及應用[J]. 農業工程學報, 2008,24(12):12-15.

[3] 張 露, 韓霽昌, 羅林濤,等. 砒砂巖與風沙土復配土壤的持水特性研究[J]. 西北農林科技大學學報(自然科學版), 2014,42(2):207-214.

[4] 李 逸, 金建新. 石羊河流域下游地區土壤水分特征曲線研究[J]. 節水灌溉, 2014,(7):10-11.

[5] 李曉鵬, 張佳寶, 吉麗青,等. 土壤傳遞函數在計算土壤飽和導水率中的應用[J]. 灌溉排水學報, 2009,28(2):70-73.

[6] 舒凱民, 樊貴盛. 基于Kostiakov二參數入滲模型參數的BP預測[J]. 節水灌溉, 2016,(10):1-5.

[7] Vereecken H J, Maes J, Feyen J, et al. Estimating the soil moisture retention characteristic from texture, bulk density, and carbon content[J]. Soil Science, 1989,148(6):389-403.

[8] Gardner W R，Hillel D，Benyamini Y. Post-irrigation movement of soil water:I. Redistribution[J]. Water Resources Research，1970，6(3):851-861.

[9] Gardner W R，Hillel D，Benyamini Y. Post-irrigation movement of soil water:P. Simulations Redistribution and evaporation[J]. Water Resources Rrsearch，1970，6(4):1 114-1 153.

[10] 蘇 楊, 朱 健, 王 平,等. 土壤持水能力研究進展[J]. 中國農學通報, 2013, 29(14):140-145.

[11] 馮永軍, 聶俊華, 張 紅. 土壤持水性能及影響因素[J]. 山東農業大學學報(自然科學版), 1996,(3):298-302.