紅壤涌泉灌水分入滲試驗及數值模擬

趙新宇，吳榮清，梁欣欣，楊彥芬

(南昌工程學院，南昌 330099)

涌泉灌是采用加流量控制器的塑料細管作為灌水器與毛管相連接，并且可以與田間滲水溝輔助，以細流或射流局部濕潤作物根區附近土壤，進行灌溉的一種灌溉方法[1]。涌泉灌解決了滴灌灌水器容易堵塞的問題，尤其適用于果樹的灌溉，在水果產區應用很多。近年來國內外學者對涌泉灌技術進行了一些研究，如：吳端普進行了龍眼果樹涌泉灌的效益分析[2]；譚明在我國西北干旱地區砂質土地上研究了果樹涌泉灌的優缺點[3]；楊素哲進行了涌泉灌大田作物的試驗研究[4]；蔣岑進行了干旱地區紅棗樹涌泉灌的技術研究[5]。但目前有關涌泉灌的理論研究還不多，本文通過室內試驗與Hydrus-3D軟件模擬，以南方紅壤土為例，研究了在不同流量下涌泉灌的土壤水分運動規律，其成果可為灌水技術要素的制定提供理論支撐。

1 涌泉灌土壤入滲試驗

1.1 供試土壤的物理性質

試驗在鄱陽湖水工程安全與資源高效利用國家地方聯合工程實驗中心開展，試驗紅壤土樣取自江西省進賢縣。將試驗土樣風干、粉碎、過2 mm篩，用塑料薄膜覆蓋保存備用。試驗開始前測得土壤初始含水率為0.036，容重1.30 g/cm3土樣的飽和導水率為2.141×10-5cm/s。使用BT-9300H(激光粒度儀)進行土壤顆粒分析，供試土壤的機械組成見表1。

采用高速離心機測定土壤水分特征曲線，使用定水頭法測定土壤飽和導水率，運用VG模型(Van Genuchten)擬合土壤水分特征曲線見表2[6]。

表2 土壤的水力特性參數Tab.2 Hydraulic parameters of experiment soils

1.2 試驗裝置與方法

試驗裝置由馬氏瓶、支架、玻璃轉子流量計和透明玻璃土箱組成。采用量程為10～100 mL/min的玻璃轉子液體流量計調節出水流量，調好流量后開始試驗，土箱尺寸為 50 cm×50 cm×50 cm。試驗裝置如圖1所示。

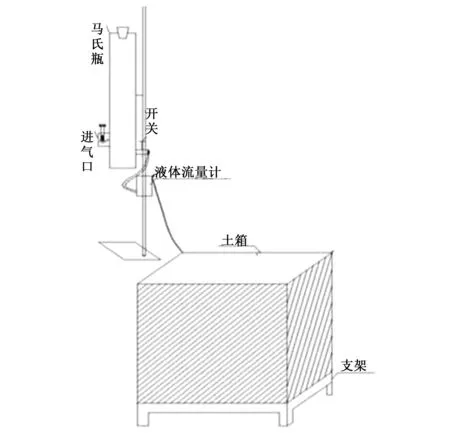
圖1 涌泉灌試驗裝置示意圖Fig.1 Experiment equipment for bubbled irrigation

在土壤密度相同，初始含水率相同的條件下，采用2、4、6 L/h等3個流量水平進行試驗。實驗開始前，用量筒校核出水口流量。試驗開始后用秒表計時，記錄下濕潤鋒在水平方向的擴散距離、垂直方向的入滲距離，并讀取同時刻馬氏瓶的刻度；由于水分入滲較快，逐一測量會存在延遲性造成誤差，故先用筆在土箱側面描繪處濕潤鋒的位置，待結束供水后在詳細測量記錄。 當供水流量為4、6 L/h時，會有積水出現。灌水結束10 min后，先用取表層5 cm土樣，再用自制取土器按照圖2所示位置分別取出土，然后烘干測定所取土壤的含水率。

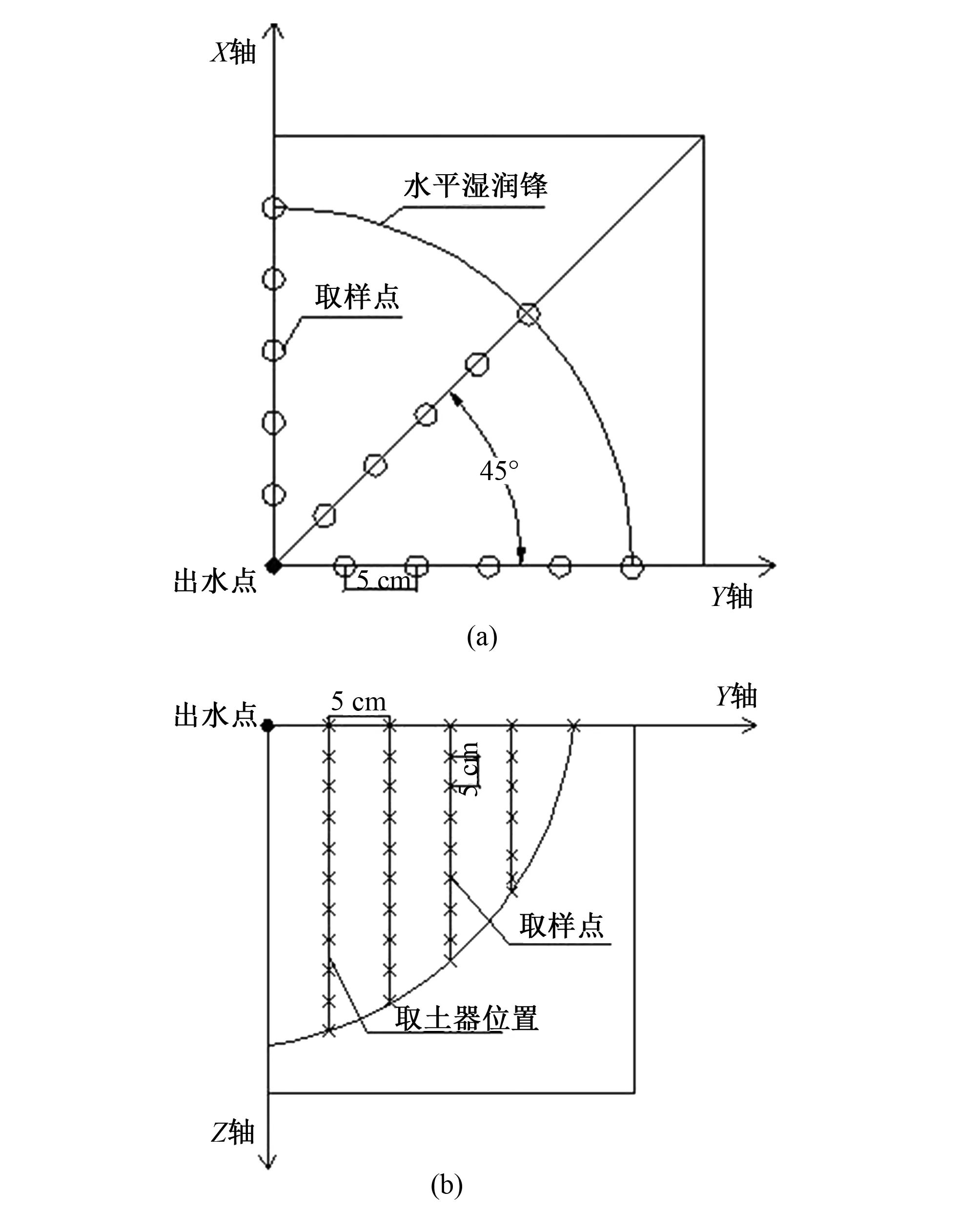
圖2 涌泉灌取樣點分布圖Fig.2 The schematic diagram of bubbled irrigation sampling points arrangement

2 土壤水分運動數學模型

2.1 土壤水分運動方程

基本假定：試驗所用土壤是均質的且各項同性，空氣、溫度、土壤水分數量和能量關系的滯后對土壤水分運動的影響是忽略的。

涌泉灌水分入滲屬于三維非飽和土壤水分運動。根據Darcy定律和質量守恒定律，土壤水分運動用理查茲方程描述[6]：

(1)

式中：θ為土壤體積含水率，cm3/cm3；t為時間，min；x、y、z為直角坐標，cm；K(θ)為土壤非飽和導水率，cm/min；ψm為基質勢，cm。

2.2 定解條件

2.2.1 初始條件的設定

假定土壤初始含水率在計算區域內是分布均勻，求解土壤水分運動方程的初始條件是：

h(x,y,z,t)=h0(x,y,z)

(2)

0≤x≤X,0≤y≤Y,0≤z≤Z,t=0

式中：h0(x,y,z)為土壤初始負壓力水頭，cm。

參照實際試驗情況來設定這一參數，同時假定土壤負壓力水頭均勻分布在計算區內，初始值設為-13 000 cm，相應實測初始含水率0.041 cm3/cm3。X、Y、Z分別對應于模擬區域橫向、縱向及垂向坐標，相應的試驗土箱，尺寸分別為：X=50 cm,Y=50 cm,Z=50 cm。

2.2.2 邊界條件的設定

圖3為模擬涌泉灌土壤水分運動計算區域示意圖，坐標原點為出水口點O，對應室內試驗，不考慮蒸散發及降雨強度，因此上邊界OEFG為零通量邊界。考慮地下水的埋深，下邊界ABCD設置成第一類邊界。邊界OABG和邊界OADE為出水口中心入滲面，由于對稱性，為零通量邊界。由于比較大的模擬計算區域，故可認為水分無法到達邊界CDEF和BCFG，水通量為零，故也為零通量邊界。邊界條件可表示為：①邊界OEFG處，不考慮降雨和蒸發強度時，q=0；②邊界ABCD處：h(x,y,z,t)=h0，0≤x≤X，0≤y≤Y，z=-Z，t≥0；③邊界CDEF處：h(x,y,z,t)=h0，0≤x≤X， -Z≤z≤0，y=Y，t≥0；④邊界BCFG處：h(x,y,z,t)=h0，-Z≤z≤0，0≤y≤Y，x=X，t≥0；⑤邊界OABG處：?h/?y=0，0≤x≤X，-Z≤z≤0，y=0，t≥0；⑥邊界OADE處：?h/?x=0，-Z≤z≤0，0≤y≤Y，x=0，t≥0；⑦出水口O處：h=H(動水頭邊界)。

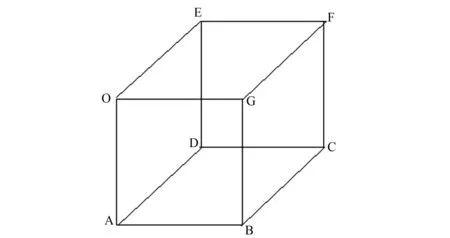
圖3 計算區域Fig.3 Calculation area

2.2.3 數值求解方法

HYDRUS-3D[7]是由Simunek等人開發的有限元計算軟件，可用于模擬土壤水流運動、溶質運移、熱量傳輸與根系吸水等過程。采用HYDRUS-3D求解數學模型，數學模型的計算采用迦遼金有限單元法，利用隱式差分法[8]離散時間，迭代規則和容忍誤差均按默認設置。采用三棱柱網格劃分計算區域，網格大小設為1.50 cm，利用從密到疏的規律配置從上到下的網格。為了同試驗結果做對比，同時驗證濕潤體內部土壤含水率，按照水平間距為5 cm，垂直間距為5 cm在計算區內設置16個觀測點，如圖4所示。

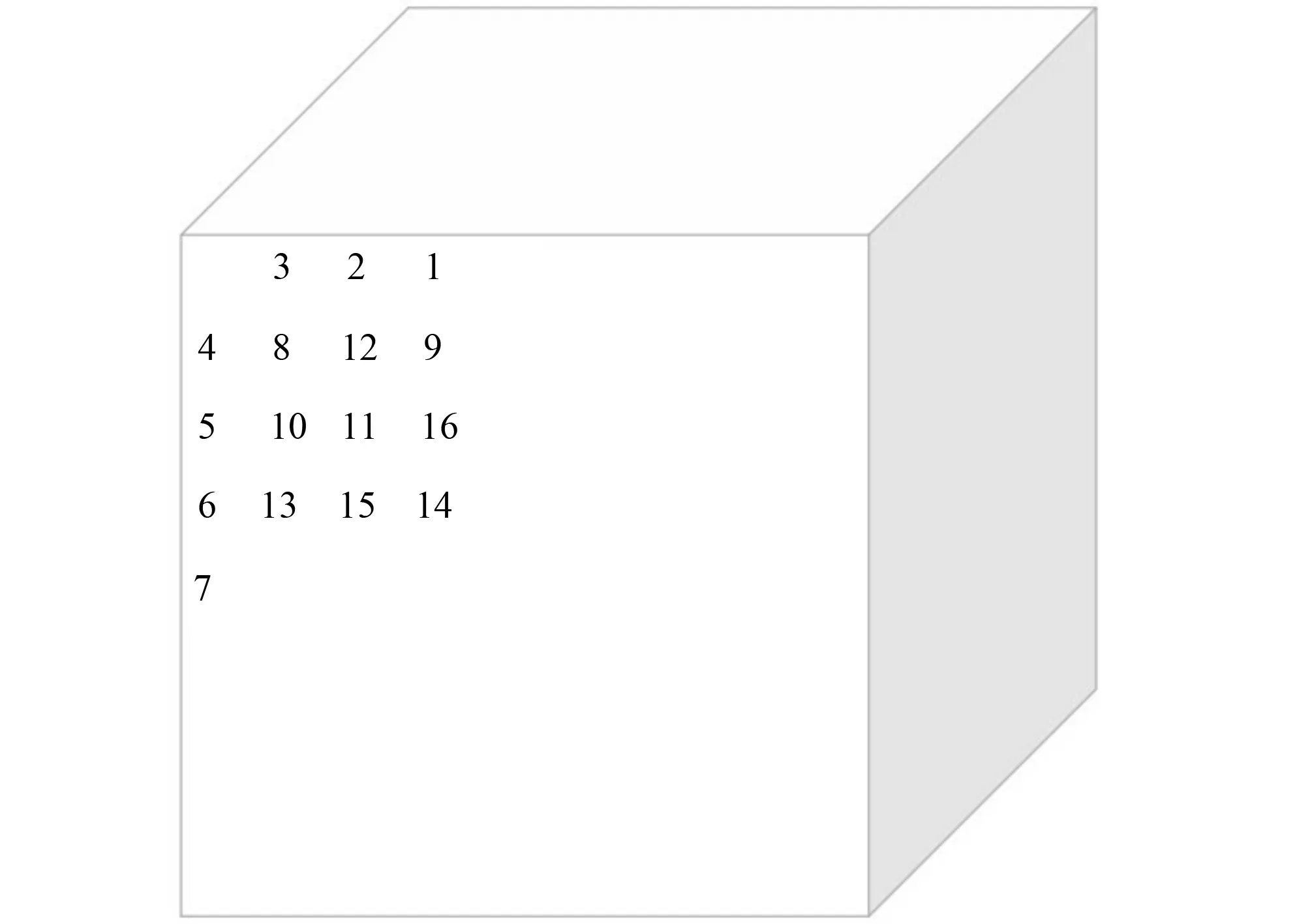
圖4 觀測點Fig.4 Observation points

3 模型驗證

表3列出試驗水平Q=2 L/h、Q=4 L/h、Q=6 L/h，T=8 h時，土壤含水率試驗實測值和模擬值。可以看出，含水率的試驗值和模擬值之間的相對誤差在0.08%～13.60%之間，誤差在距離出水口較遠的地方較大。產生這些誤差的主要原因可能是室內土箱裝土時，人工夯土不均勻。儀器測量時引起的滯后效應也會產生誤差。另外，土壤水勢計算時，水分特性曲線轉變成土壤含水量也造成一定的誤差。總體而言，試驗結果與模擬結果誤差較小，兩者較好的一致性，涌泉灌的土壤水分運動可用該模型來模擬。

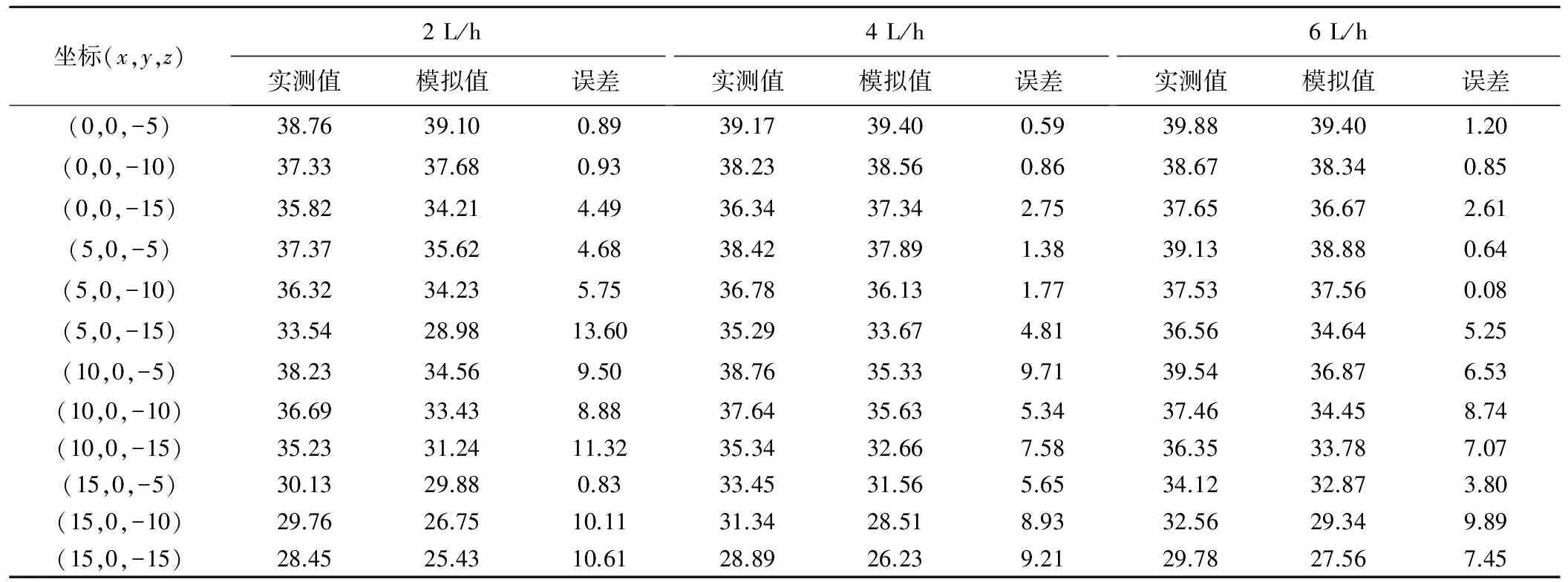
表3 土壤實測含水率與模擬含水率的對比 %

4 不同流量條件下土壤水分運動的數值模擬

通過驗證的HYDRUS-3D模型，可以對不同的土壤密度、初始含水率、流量等條件下的紅壤涌泉灌水分入滲進行數值模擬，為滲泉灌灌水參數的制定提供理論支撐。本文進行了不同流量條件下的土壤水分入滲的數值模擬與分析。

4.1 流量對濕潤體形狀的影響

模擬灌水流量為Q=2 L/h、Q=4 L/h、Q=6 L/h，灌水時間為T=2 h、T=4 h、T=8 h時濕潤體土壤含水量如圖5所示。不同流量條件下，隨著流量的增大，濕潤體形狀相應變大；隨著時間的推移，入滲的水平半徑、入滲的豎直深度漸漸變大；但隨時間的增加，入滲的幅度漸漸減小，即濕潤體擴散速率在水平和豎直方向不斷減小。相同流量下，同一時間內土壤水分向下入滲距離比水平擴散距離大，濕潤鋒豎直比水平運移距離大，濕潤體近似橢球體。隨著流量變大，濕潤鋒在豎直與水平方向的移動距離差異變大，濕潤體更趨于扁平。

圖5 涌泉灌土壤剖面體積含水率分布Fig.5 Bubble Irrigation volumetric water content in soil profile distribution

隨著灌水時間的延長，灌水量不斷增多，濕潤體逐步擴大，濕潤的輪廓線不斷向外延伸，但推進的速度的變慢。濕潤體內的高含水區的含水量接近飽和值，流量越大，高含水區的范圍就越大。這是因為土壤入滲能力小于供水強度，經過一段時間的灌水，出水口土壤表層產生積水，這樣就造成在積水區域周圍的土壤含水率快速達到飽和狀態，促進水平方向的擴散；在重力勢能和基質勢能的作用下，隨著土壤水勢梯度遞減，土壤水在垂直方向的運動增大，所以隨著流量的變大濕潤體內高含水區的范圍也相應變大。

4.2 流量對土壤含水率的影響

以A點(0，0，-10)和B點(-10，0，-10)為例，分析土壤含水率在不同流量下的變化情況，兩點的含水率變化曲線如圖6所示。

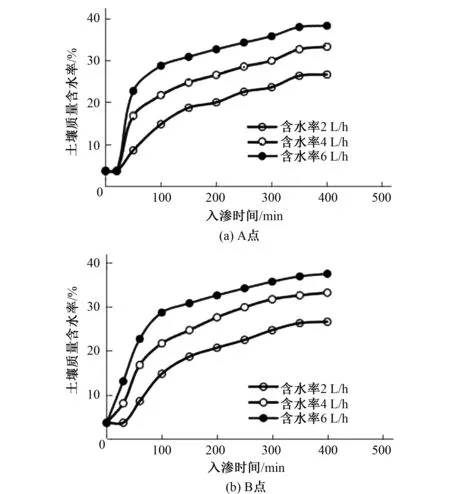
圖6 流量對土壤體積含水率的影響模擬Fig.6 Simulation of the effect of flow on soil moisture content

在位置不同的A、B兩點，當濕潤鋒到達時，含水量迅速增加，隨著灌水的時間逐漸增大，變化趨勢趨于平緩，最后接近于穩定，這說明隨著流量的增加，土壤水分運動特征值也隨之變大，變化幅度隨著時間的增加而減小。B點至入滲點O的距離較大，在入滲開始階段，A點的土壤含水量上升較快，隨著時間的增長，兩點的土壤含水量趨近于相同，當流量為Q=6 L/h時，土壤含水率接近于飽和。

當流量不相同時，流量越大，濕潤鋒經過A、B兩點所需時間越少；流量越大，土壤含水率增加的速率越快；土壤含水率隨流量的增大而增大。隨著時間的推移，不同入滲流量的三條土壤含水量曲線接近于平行，說明當入滲穩定后，土壤含量與入滲流量呈等比例增加的關系。另外，在距離出水口同一距離，隨著土壤在豎直方向的深度增加，濕潤體內的含水率漸漸變小；同一土壤深度，距離出水口距離越大，濕潤體內含水率越小。

5 結 語

通過不同流量的紅壤涌泉灌水分入滲實驗與HYDRUS-3D數值模擬，研究了涌泉灌土壤水分運動，研究結果表明：

(1)涌泉灌室內入滲實驗與HYDRUS-3D數值模擬的土壤含水率相對誤差在0.08%～13.60%之間，兩者具有較好的一致性，該模型能比較好地反映涌泉灌的三維土壤水分入滲運動，可以用于紅壤涌泉灌水分運動的模擬。

(2)數值模擬說明：土壤水分入滲濕潤體的形狀接近于橢圓形，濕潤體的大小、濕潤體內高含水區域的大小隨入滲流量的增大而增大；隨著土壤豎直深度、水平距離的增大，濕潤體內的含水率漸漸變小；隨著流量的增加，土壤水分運動特征值增大，變化幅度隨時間的增加而減小；入流量越大，濕潤鋒運移速度越快，土壤含水率增加的速率越大；當入滲穩定后，土壤含水量與入滲流量呈等比例增加的關系。

[1] 楊素哲，沈菊艷，黃寶全，等. 果樹涌泉灌溉方式的技術應用[J]. 農業工程學報，2005，21，(S1):68-71.

[2] 吳端普，洪波濤，李曉瑜，等. 龍眼需水量及微噴灌增產效益分析[J].中國農村水利水電，2002，(3):28-30.

[3] 譚 明. 涌泉灌技術應用[J].節水灌溉，2003，(6):24-26.

[4] 楊素哲，陳玉民，黃寶全. 涌泉灌技術在大田作物灌溉中的試驗研究[J].節水灌溉，2005，(3):32-34.

[5] 蔣 岑，謝香文，王長新，等. 模糊數學在干旱區成齡棗樹微灌技術選擇中的應用[J].節水灌溉，2010，(1):9-11.

[6] 李春友，任 理，李保國.利用優化方法求算Van Genuchten方程參數[J].水科學進展，2001，12(4):473-477.

[8] Lubana P P S, Narda N K.Soil water dynamics model for trickle irrigated tomatoes[J]. Agricultural Water Management,1998,37(2):145-161.