空間回歸模型設(shè)定方法探討

劉 明

（蘭州財經(jīng)大學(xué)a.甘肅經(jīng)濟發(fā)展數(shù)量分析研究中心；b.統(tǒng)計學(xué)院，蘭州 730020）

1 問題的提出

新經(jīng)濟地理學(xué)的出現(xiàn)與發(fā)展，使得人們越來越關(guān)注經(jīng)濟社會的區(qū)域空間問題。作為空間因素研究的重要工具，空間回歸模型以及在此基礎(chǔ)上建立的經(jīng)濟學(xué)分支學(xué)科——空間計量經(jīng)濟學(xué)受到了廣泛的關(guān)注和討論，為新經(jīng)濟地理學(xué)的研究提供了重要的方法支持。在國內(nèi)的空間計量經(jīng)學(xué)應(yīng)用研究的主要文獻里，可以發(fā)現(xiàn)很多文獻無論是對問題本質(zhì)的洞察力還是建模技巧，乃至技術(shù)上的處理都非常精致。但部分文獻中還存在一些問題，其中一個重要問題就是模型形式設(shè)定有待于推敲，諸如在構(gòu)建或選擇空間回歸模型時沒有給出詳細的說明和解釋、沒有聯(lián)系實際問題就模型設(shè)定進行探究、模型變量的確定未經(jīng)過細致的分析等問題，致使這些模型在文獻中略感突兀，顯現(xiàn)出“死搬硬套”的痕跡，這樣就容易使問題研究的價值和可信度大打折扣。空間相關(guān)性在經(jīng)濟現(xiàn)象中確實普遍存在，但空間回歸模型未必能夠解釋、解決一切問題，因此在實際問題研究中不能動輒就套以空間回歸模型。誠然，考慮空間因素的回歸模型確實較經(jīng)典回歸模型高一層次，甚至說是回歸模型發(fā)展的一個質(zhì)的飛躍，但也不是所有的問題都可以拿來套用空間回歸模型。這些現(xiàn)象從某種角度來說，是反映了我國空間計量經(jīng)濟學(xué)發(fā)展的不成熟，方法討論和實際應(yīng)用還沒有完全結(jié)合起來。基于此，本文通過對空間回歸模型設(shè)定偏誤問題進行分析，進一步討論在實際應(yīng)用中如何構(gòu)建一個正確的空間回歸模型，以求對模型應(yīng)用技術(shù)的完善。

2 常用的空間回歸模型及關(guān)系

空間回歸模型中以空間自回歸模型（SAR）、空間誤差模型（SEM）以及空間杜賓模型（SDM）最為基礎(chǔ)亦最為常見。如果回歸模型中被解釋變量在空間上與其相鄰區(qū)域的變量（也是被解釋變量）存在空間相關(guān)性，那么可以將這種相關(guān)性引入到回歸模型中，從而構(gòu)造出空間自回歸模型。空間自回歸模型形式為：

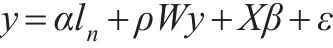
或

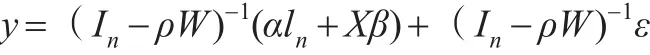
其中，y和X分別為被解釋變量向量和解釋變量矩陣，W為權(quán)重矩陣，ln為n階單位向量，α、ρ、β分別為截距參數(shù)、空間效應(yīng)參數(shù)和回歸參數(shù)，ε為隨機干擾向量，且假定ε～N(0,σ2In)。為討論方便，通常將ln與X合并，將SAR模型直接寫為：

將模型（1）的空間自相關(guān)項ρWy移至等式左邊可得：

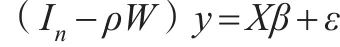
于是有：

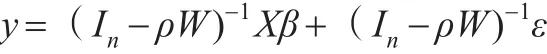
令=（In-ρW)-1X，u=（In-ρW)-1ε，則可以得到：

模型（2）即為空間誤差模型（SEM），其特征是模型隨機項u存在空間依賴。

實際應(yīng)用中時常出現(xiàn)模型選擇的不確定性，即無法確定應(yīng)該選擇哪一個模型來對問題進行建模研究。假設(shè)這種情況出現(xiàn)在SAR模型和SEM模型之間，兩類模型形式分別為：

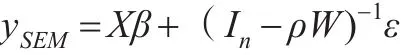
令這兩個模型出現(xiàn)的概率各自為πSAR、πSEM，且πSAR+πSEM=1，也就是說，實際的模型形式滿足：

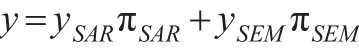
將SAR模型和SEM模型代入并計算可得：

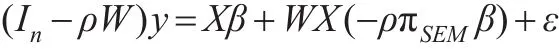
令β1=β，β2=-ρπSEMβ，則可得到模型（3）：

模型（3）即為空間杜賓模型（SDM）。上述分析表明，SDM模型是SAR模型和SEM模型的線性組合。

由變量的空間自相關(guān)現(xiàn)象引出SAR模型，通過對SAR模型的分析得到SEM模型，進一步對SAR模型和SEM模型進行線性組合得出SDM模型，由此可以看出這些模型之間的聯(lián)系。在空間計量經(jīng)濟學(xué)中，這三類模型是最為基礎(chǔ)也是最為常見的空間回歸模型。

3 常見的模型設(shè)定偏誤分析

空間回歸模型的形式不僅局限于上述幾類，在不同的情形下有諸多的拓展形式。在具體的問題研究中，從理論上講最優(yōu)的模型只有一個，因此在實際問題研究中構(gòu)造能正確表述客觀事實、符合實際研究需要的空間回歸模型——即實現(xiàn)模型的正確設(shè)定，是一件重要且不易做到的事。一些模型的構(gòu)建者在研究實際問題時出現(xiàn)了模型設(shè)定偏誤。這些設(shè)定偏誤的出現(xiàn)可能因為建模者對所研究的問題把握不夠、存在認識偏差，或沒有遵循事物的運行規(guī)律和特征，或者將模型形式設(shè)計得過于簡化，這些都是建模過程中普遍出現(xiàn)的問題。除此之外，對于空間回歸模型而言，出現(xiàn)設(shè)定偏誤的原因可能有如下方面：

首先是未考慮空間因素，或空間因素考慮得不夠全面。在經(jīng)濟學(xué)問題研究中，由于貿(mào)易交流、示范效應(yīng)等因素的存在，使得地域關(guān)聯(lián)性越來越受到研究者的重視。對于傳統(tǒng)的認為經(jīng)濟運行發(fā)展過程中地域間不相關(guān)的觀點，或者是模型構(gòu)建過程中關(guān)于地域間不相關(guān)的假設(shè)條件，已不合時宜且不符合實際。因此，在經(jīng)濟模型構(gòu)建過程中，尤其是存在區(qū)域坐標(biāo)的經(jīng)濟問題研究中，空間因素是必須要考慮的對象。在此情形下若不考慮空間依賴因素而直接構(gòu)建模型，就極有可能造成模型設(shè)定的錯誤。另外，在構(gòu)建空間回歸模型時，對于空間因素考慮得不夠全面也是造成模型設(shè)定偏誤的重要原因，例如在一個多變量的經(jīng)濟系統(tǒng)中，僅考慮了某一個或某一部分變量的空間依賴性，而忽略了另一些變量的空間依賴作用，此時構(gòu)建的空間回歸模型的形式也是錯誤的。假設(shè)正確的空間回歸模型的形式為：

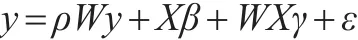
由于空間依賴因素考慮得不全面，忽略了解釋變量X的空間依賴性，使得模型設(shè)定為：

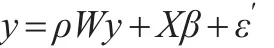
顯然，ε′=WXγ+ε，它和解釋變量X是相關(guān)的，可以證明，此情形下的參數(shù)β的估計量（MLE及OLS）是有偏且不一致的（證明過程可依照普通線性回歸模型遺漏變量的情景來進行）。因此需要全面考慮變量的空間相關(guān)性才能保證模型設(shè)定的正確。因此，在構(gòu)建空間回歸模型時不僅要考慮空間因素是否存在，也要考慮空間依賴關(guān)系是否全面。

造成空間回歸模型設(shè)定偏誤的另一原因是遺漏重要解釋變量。不妨假設(shè)正確的模型形式為：

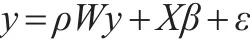
如果遺漏了重要的解釋變量X，則模型被錯誤的設(shè)定為：

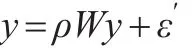
不難發(fā)現(xiàn)，ε′=Xβ+ε。假設(shè)X存在有空間自相關(guān)，即X=θWX+?（∈與ε不相關(guān)），此時：

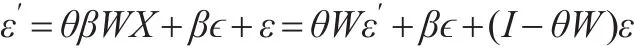
顯然，模型隨機項ε′存在有空間自相關(guān)問題，此時若直接對模型y=ρWy+ε′進行估計和分析而忽略隨機項的自相關(guān)問題，其結(jié)果必定都是錯誤的——參數(shù)ρ的最大似然估計結(jié)果是不一致的，以此模型對所研究問題的分析是不可靠的。因此，遺漏空間回歸模型的重要解釋變量會造成模型的設(shè)定偏誤。另一種情形是，如果遺漏的解釋變量沒有空間相關(guān)性，此時對于參數(shù)ρ的估計結(jié)果具有一致性，即不影響反映空間效應(yīng)參數(shù)ρ的估計。但此時由于模型失去了部分解釋變量而顯得欠缺。

選擇錯誤的模型形式也是造成空間回歸模型設(shè)定偏誤的一個重要原因。空間回歸模型形式的選擇是一個既有科學(xué)性又有藝術(shù)性的問題。模型選擇的科學(xué)性在于依賴于已有的學(xué)科理論和知識背景設(shè)計模型的形式，同時可以對模型施加諸如拉格朗日乘數(shù)檢驗等統(tǒng)計檢驗方法以進行評判。因此，科學(xué)性使得模型形式的選擇在實際問題研究中有科學(xué)的依據(jù)。而模型選擇的藝術(shù)性在于，針對同一問題背景，不同的研究視角和研究目的，不同的研究人員，可能會選擇不同的空間回歸模型形式。換句話說，可能會因為不同的研究視角和研究目的而設(shè)定出不同的空間回歸模型，也有可能因為不同的研究人員對問題的認識不同、研究水平的不同而使得設(shè)定的空間回歸模型存在差異。因此，藝術(shù)性使得模型形式的選擇在實際問題研究中有較大的主觀性，從而使得模型形式誤設(shè)的風(fēng)險加大。

例如，正確的模型形式為SDM：

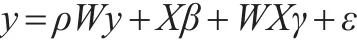
但由于某種原因誤使模型設(shè)定為SAR：

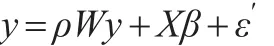
和上述分析路徑一致，由于隨機項ε′存在空間自相關(guān)且和解釋變量相關(guān)，不滿足最大似然估計的獨立性假定，因此ρ、β的估計量都是不一致的。

再如，當(dāng)檢測出研究對象存在有空間依賴性時，選擇SAR模型還是SEM模型是困擾研究者的一個難題，我們可以用諸如拉格朗日乘數(shù)檢驗法來對模型加以選擇，但這在有些問題中未必有效（例如數(shù)據(jù)的生成形式既包含SAR也包含SEM）。此時錯誤的模型形式會有較大的成本。如果正確的模型是一個SAR模型：

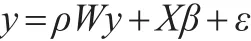
但研究人員設(shè)計了一個SEM：

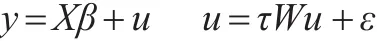
由于SEM模型中沒有考慮到被解釋變量y的客觀存在的空間自相關(guān)性，因此在隨機項u中存在空間自相關(guān)。所以SEM模型是可估的。但針對這類模型設(shè)定偏誤，毫無疑問，研究人員失去了估計y的空間自回歸參數(shù)ρ的機會，換來的僅是隨機項u的自回歸參數(shù)τ的估計結(jié)果——它在實際問題中并不具有較多的經(jīng)濟意義，通常不被關(guān)注。同時，參數(shù)β的估計量也會發(fā)生偏倚。可以運算證明，SAR和SEM模型的參數(shù)β的估計量可以表示為：

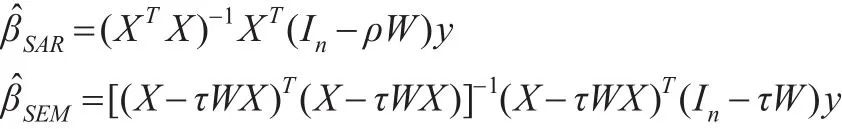
4 正確設(shè)定空間回歸模型的途徑

對于多種類型的空間回歸模型，在實際問題研究中該如何選擇，即如何設(shè)定出正確的模型形式，是空間回歸模型應(yīng)用研究的關(guān)鍵。這里根據(jù)模型的數(shù)理關(guān)系及相關(guān)實證經(jīng)驗，構(gòu)造出幾類實現(xiàn)模型正確設(shè)定的思路及途徑。

4.1 理論結(jié)合數(shù)據(jù)

依據(jù)所研究問題的理論背景和現(xiàn)有的樣本數(shù)據(jù)特征來設(shè)定空間回歸模型，是實現(xiàn)模型正確設(shè)定的首要一步。在一般的經(jīng)濟學(xué)問題研究中，都會有相關(guān)的理論背景，這些理論背景包括設(shè)計該問題研究的學(xué)說、假說以及問題的內(nèi)在邏輯等，這些理論背景是完成空間回歸模型設(shè)定的重要基礎(chǔ)。一般來說，建模者需要依據(jù)實際經(jīng)濟理論和問題內(nèi)在邏輯、厘清變量間的內(nèi)在關(guān)系、全面尋找目標(biāo)變量的影響因素，設(shè)計模型的表達式。這里以消費問題研究為例對此進行說明。

在凱恩斯理論框架下可以認為消費是收入的線性函數(shù)，即絕對收入假說。杜森貝里在此基礎(chǔ)上提出了相對收入假說，該假說認為存在兩種效應(yīng)影響消費水平，即示范效應(yīng)和棘輪效應(yīng)。為對此假說進行實證檢驗，可以在凱恩斯消費函數(shù)的基礎(chǔ)上設(shè)計出能夠體現(xiàn)示范效應(yīng)和棘輪效應(yīng)特征的計量經(jīng)濟學(xué)模型。這就需要熟悉絕對收入假說理論和相對收入假說理論，為節(jié)約篇幅，相關(guān)理論背景此處不予復(fù)述。首先構(gòu)造凱恩斯消費函數(shù)：

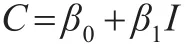
其中C為消費，I為收入，β為參數(shù)。為體現(xiàn)棘輪效應(yīng)，當(dāng)期收入會受到前期收入的影響，此時模型可進一步改設(shè)為：

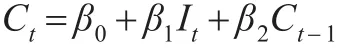
下標(biāo)t表示時間。若β2顯著大于0，則棘輪效應(yīng)存在。進一步考慮示范效應(yīng)，此時可構(gòu)造空間自回歸模型：

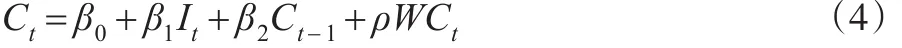
其中W是空間權(quán)重矩陣。如果ρ顯著大于0，則示范效應(yīng)存在。模型（4）即為根據(jù)相關(guān)消費理論背景所設(shè)定的空間回歸模型。

在一些實際問題研究中，有可能存在“無理可依”的情形，即沒有既成的理論來指導(dǎo)建模，這時可以根據(jù)樣本數(shù)據(jù)的特征、通過探索樣本數(shù)據(jù)的規(guī)律來構(gòu)建空間回歸模型。這里主要是通過檢驗變量的空間相關(guān)性、考察空間分布信息以及變量間的空間依賴形式來進行探索式建模。更多情形下，可以將理論指導(dǎo)型建模方法和數(shù)據(jù)探索型建模方法結(jié)合起來，這樣可以使得模型更為客觀且容易發(fā)現(xiàn)新問題。例如，在上述基于相對收入假說構(gòu)建的空間回歸模型中，可以進一步考察收入的空間相關(guān)性問題——這是有必要的，因為收入水平常出現(xiàn)空間集聚現(xiàn)象，這或許可以發(fā)現(xiàn)有關(guān)收入-消費的一些新問題。

4.2 用另一空間回歸模型替代

在一些模型的構(gòu)建過程中，可能會因為種種原因而無法構(gòu)造出原有的正確模型，這時選擇合適的空間回歸模型在一定程度上可以緩解甚至解決模型設(shè)定偏誤的影響。例如，在構(gòu)建統(tǒng)計模型時，可能會遺漏一些變量，這些變量可能是次要因素而不必要列入模型中，也可能是主要因素但無法觀測而不得不舍棄，更或是建模者的水平有限而造成模型誤設(shè)。如果模型遺漏的變量存在有空間自相關(guān)，一般可以考慮設(shè)定空間杜賓模型來加以修正。

為說明這一問題，本文設(shè)定一個空間回歸模型，不妨假設(shè)某一因變量y完全可以由兩個解釋變量x和z來解釋：

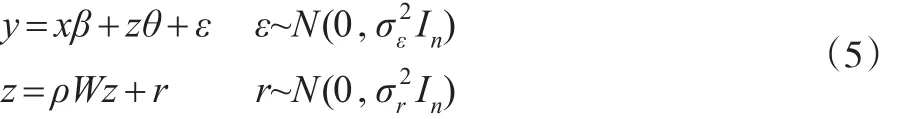
其中W是空間權(quán)重矩陣，此線性空間模型很容易求解參數(shù)β、θ。若變量z被“遺漏”，那么z的信息被歸并到模型隨機項之中。此時，參數(shù)θ因z被遺漏而不存在，需要估計的參數(shù)為β。顯然，直接估計模型“y=xβ”無法得到β的正確估計結(jié)果。另外，直接使用空間誤差模型（將變量z的空間形式帶入到回歸模型中并適當(dāng)化簡即可得到空間誤差模型的形式，變換過程略）：

也不能估計出正確的β，因為此時沒有考慮x與u相關(guān)性——現(xiàn)實中由于x與u很可能相關(guān)（因為x和z很可能相關(guān)），此時β的估計量可能有偏且不一致。考慮到x與u的相關(guān)性，不妨假設(shè)為簡單線性相關(guān)：

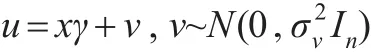
在此情形下，可以在模型（6）的基礎(chǔ)上進一步將模型改寫為：

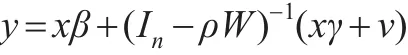
或

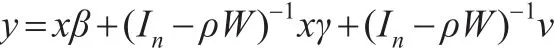
稍做變換即可發(fā)現(xiàn)，此即為空間杜賓模型：

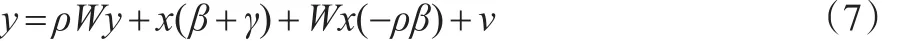
此時隨機項ν和解釋變量x不相關(guān)。模型（7）參數(shù)ρ、-ρβ都是可估計的，且得到的都是一致估計量，因而參數(shù)β也可估計且是一致估計量。因此，空間杜賓模型可以解決遺漏具有空間相關(guān)性的變量的影響，這可以得到參數(shù)的正確估計結(jié)果進而優(yōu)化此類模型的設(shè)定效果。

4.3 借助于統(tǒng)計檢驗

判斷空間回歸模型設(shè)定的合理性，一個重要的手段就是進行統(tǒng)計檢驗，即所謂的模型設(shè)定檢驗。模型設(shè)定檢驗通常是一種事后檢驗方法，即將模型形式設(shè)定出以后，通過已知的樣本數(shù)據(jù)信息檢驗判斷模型設(shè)定是否合理。一個常見的模型設(shè)定問題是，到底是選擇SAR模型還是選擇SEM模型更為合理？為此，Anselin（1988）提出了針對SAR模型的檢驗方法，它是通過構(gòu)造拉格朗日乘數(shù)（LM統(tǒng)計量）來完成，簡記為LM-Lag檢驗，此檢驗可判斷是否應(yīng)該將模型設(shè)定為SAR形式。Burridge（1980）提出了針對SEM模型的LM統(tǒng)計量，即所謂的LM-Error檢驗，用來判斷是否應(yīng)該將模型設(shè)定為SEM的形式。對于SEM模型是否存在遺漏變量問題，可以使用Hausman檢驗來加以判斷。用于直接或間接判斷空間回歸模型的統(tǒng)計檢驗方法較多，此處不再細述。

4.4 針對特定問題的模型形式

在諸多形式的空間回歸模型中，有些模型是針對于一些特定問題研究的，或者說針對于某一特定問題，只能用某類特定的空間回歸模型。在這些問題研究中，如果能熟悉問題和模型之間的聯(lián)系，那么設(shè)定出正確的回歸模型便相對容易。

例如，用于研究局部空間問題的空間地理加權(quán)模型（GWR）：

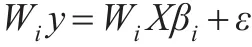
其中βi表示與位置i對應(yīng)的參數(shù)。Wi是n×n的加權(quán)矩陣，主對角線上的每個元素都是關(guān)于觀測值所在位置j與回歸點i的位置之間距離的函數(shù)，其作用是權(quán)衡不同空間位置j(j=1,2,…,n)的觀測值對于回歸點i參數(shù)估計的影響程度，非主對角線元素全部為0。運用最小二乘法可得到參數(shù)βi的估計量：=(XTWiX)-1XTWiy，這樣，對于不同的觀測區(qū)域可以得到不同的參數(shù)估計結(jié)果，以展示不同觀測區(qū)域之間的差異性。因此，當(dāng)研究局域空間依賴性、考察不同區(qū)域的差異性及空間變動特征時，通常考慮設(shè)定GWR模型。

再例如，在貿(mào)易領(lǐng)域，經(jīng)濟體之間的空間距離是影響雙邊貿(mào)易的重要因素。一種理論認為，經(jīng)濟體之間的單項貿(mào)易流量與它們各自的經(jīng)濟規(guī)模成正比，與它們之間的距離成反比。由此觀點構(gòu)造出著名的空間引力模型：

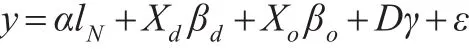
上述模型是LeSage和Pace（2008）在有關(guān)理論基礎(chǔ)上構(gòu)造的。這里假設(shè)有n個樣本區(qū)域，每個樣本區(qū)域都既是“來源地”又是“目的地”，這樣就會有N(N=n×n)組觀測數(shù)據(jù)。模型中，被解釋變量y是N×1階列向量；解釋變量X是N×k階矩陣；D是由“來源地”到“目的地”的距離構(gòu)造的N×1階矩陣；lN是N個1組成的列向量；ε為服從經(jīng)典假定的隨機擾動項；下標(biāo)“o”代表“來源地”，下標(biāo)“d”代表“目的地”；α、βd、βo及γ為待估參數(shù)。空間引力回歸模型是研究雙邊乃至多邊貿(mào)易影響關(guān)系的重要工具，它在研究地域貿(mào)易關(guān)系時非常有用，因為相關(guān)區(qū)域的路徑距離是影響貿(mào)易的重要因素之一。這也正是新經(jīng)濟地理學(xué)的核心思想。因此，在區(qū)域經(jīng)濟貿(mào)易問題的研究中通常考慮設(shè)定此模型。

5 總結(jié)與思考

模型設(shè)定問題一直是應(yīng)用計量經(jīng)濟學(xué)中一個重要的議題，模型設(shè)定正確與否關(guān)系到整個應(yīng)用研究的成敗。空間回歸模型較經(jīng)典回歸模型更為復(fù)雜，因為其考慮了區(qū)域個體間的依賴關(guān)系，因而在設(shè)定過程中需要考慮更多的影響因素。本文重點在SAR模型、SEM模型和SDM模型基礎(chǔ)上，討論分析了未考慮空間因素或未完全考慮空間因素、遺漏重要解釋變量、選擇了錯誤的模型結(jié)構(gòu)等空間回歸模型設(shè)定偏誤的不良后果，這些設(shè)定偏誤在實際問題研究中較為常見，對這些設(shè)定偏誤的分析有助于警示建模者盡量避免這些類型的設(shè)定偏誤。對于如何設(shè)定出正確完善的空間回歸模型，現(xiàn)實中還沒有切實的理論可循，但可以針對于一些較具體的情形總結(jié)出一些經(jīng)驗方法。本文在討論空間回歸模型設(shè)定偏誤的基礎(chǔ)上進一步提出了“理論結(jié)合數(shù)據(jù)”、“使用可替代的空間回歸模型”、“借助于統(tǒng)計檢驗”以及“使用特定模型”等一些來源于建模實踐的設(shè)定出正確空間回歸模型的思路與方法，通過結(jié)合實際經(jīng)濟問題、推演論證，證明這些思路與方法是可行的，有助于實現(xiàn)空間回歸模型的正確設(shè)定。

當(dāng)然，實現(xiàn)空間回歸模型正確設(shè)定的方法也不僅局限于本文所提出的，本文也只是對一些常見的、主要的設(shè)定方法概而述之，在警示空間回歸模型存在錯誤的設(shè)定形式會造成不良后果的同時，進一步提出問題的解決思路與方向，但這并不能形成理論體系或者教條，實際上在很多情況下仍需要具體問題具體分析。如何在實際應(yīng)用中提高空間回歸模型的設(shè)定效率、改進模型設(shè)定效果，仍需要進一步的探索研究。但目前的情況是，人們對這一問題并沒有太多的關(guān)注，原因有兩點：一是模型設(shè)定問題的研究沒有既成的理論框架，也難以形成理論框架，更多的需要結(jié)合研究經(jīng)驗；二是模型設(shè)定問題是一個邊緣化的問題，它似乎既不屬于空間回歸模型的理論研究，也不屬于應(yīng)用研究。人們更愿意在已有理論框架的學(xué)術(shù)領(lǐng)域或在實際應(yīng)用領(lǐng)域進行研究探索，但這些并不說明空間回歸模型設(shè)定問題不重要，相反，空間回歸模型設(shè)定方法是將空間回歸模型理論成功應(yīng)用于經(jīng)濟問題實踐的橋梁。

另外，本文重點討論的是空間回歸模型形式設(shè)定問題，是在假設(shè)空間回歸模型已存在合理的空間權(quán)重矩陣的基礎(chǔ)上完成的研究，而事實上空間權(quán)重矩陣的形式與構(gòu)造也是空間回歸模型設(shè)定的一個重要議題，雖然文獻中已有很多關(guān)于空間權(quán)重矩陣構(gòu)造的理論與方法，但在實際應(yīng)用中仍顯欠缺與不足，空間權(quán)重矩陣的設(shè)定也是需要進一步討論的方向。

[1]Anselin L.Lagrange Multiplier Test Diagnostics for Spatial Dependence and Spatial Heterogeneity[J].Geographical Analysis,1988,20(1).

[2]Burridge P.On the Cliff-Ord Test for Spatial Autocorrelation[J].Journal of the Royal Statistical Society B,1980,42(1).

[3]Pace R K,LeSage J P.A Spatial Hausman Test[J].Economics Letters,2008,101(3).

[4]LeSage J P,Pace R K.Spatial Econometric Modeling of Origin-destination Flows[J].Journal of Regional Science,2008,48(5).

[5]Anselin L.Thirty years of spatial econometrics[J].Regional Science,2010,89(1).

[6]LeSage J,Pace R K.Introduction to Spatial Econometrics[M].UK:Taylor&Francis Group,2009.