變權1-AGO GM(1,1,λ)模型及其應用

蘇術鋒，潘坤友

（鹽城工學院 管理學院，江蘇 鹽城 200052）

0 引言

科學技術是“第一生產力”。技術創新是促進生產力發展的第一要素。國內外，無論是學術者，還是實際工作者，都十分重視技術創新的學術與應用的研究。因此，本文擬用灰色系統模型研究技術創新問題。

我國學者鄧聚龍教授首先創建了灰色系統學說，特別是GM(1,1)模型，在“小樣本，貧信息”的不確定系統下，成功地應用到經濟管理的各種問題中[1]。GM(1,1)模型問世以來，由于其應用廣泛，一直是國內學者研究的熱點。不少學者尋找各種方法，對GM(1,1)模型進行改進，以提高其擬合精度和預測精度。文獻[2,3]改進初始值，提高模型的精度；劉思峰（1991）提出緩沖算子概念后，文獻[4,5]在強化或弱化算子方面作了深入的研究；譚冠軍（2000）提出背景值構造方法，近年來，背景值構造方法研究十分活躍[6,7]；周偉、姚天祥、謝乃明等對GM(1,1)模型進行開拓性研究[8-10]。以上模型對不同時期數據采用等權累加，文獻[11]提出了加權累加生成模型；文獻[12]采用粒子算法，提出了變權累加生成模型。但其ρ(i)相對x(i)是不變的，所以仍然是加權問題。加權累加僅僅只能提供算子權重功能，不具備算子累加功能。文獻[13]提出了分數階累加GM(1,1)模型，但在其證明AGO表達式時，用矩陣方法從整數視角證明AGO表達式，然后將其擴展到分數形式。因為矩陣的冪不能為分數，所以這種從特殊到一般的證明方法是不正確的。文獻[14]的AGO表達式中含有組合論表達式，因為組合論未研究分數組合問題，所以這對于分數階AGO中的證明是不成立的。針對以上模型的不足，本文提出兼有累加和權重功能的變權1-AGOGM(1,1,λ)模型。它通過自定義變權函數，AGO表達式無需數學證明。

1 變權一次累加生成算子的定義與性質

GM(1,1)模型的原始形式：

定義1：非加權累加生成算子

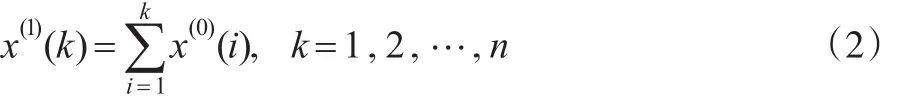
定義2：加權累加生成算子

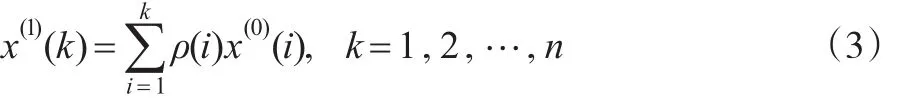
其中，權重ρ(i)相對x(0)(i)是不變的。

定義3：變權累加生成算子

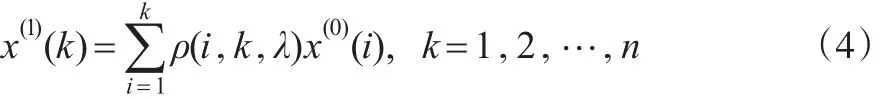
其中，λ稱為變權因子；權重ρ(i,k,λ)在不同k條件下，相對x(0)(i)是變化的。

定理1：加權或變權算子對于式（1）不成立。

證明：

（1）當ρ為加權時，ρ是i的函數，即ρ(i)

當非加權時，對于式（1）來說，恒有x(1)(k)-x(1)(k-1)=x(0)(k),k=2,3,…,n

當加權時，得：

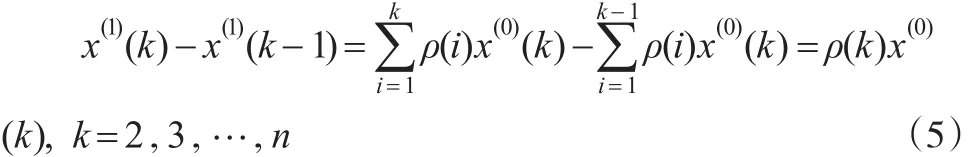
因為是加權，所以ρ(k)不可能全部等于0或1，所以由式(5)可知：

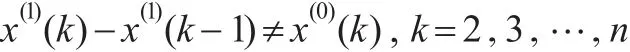
（2）若ρ(i,k,λ)是變權，則：ρ是i,k,λ的函數，即ρ(i,k,λ)

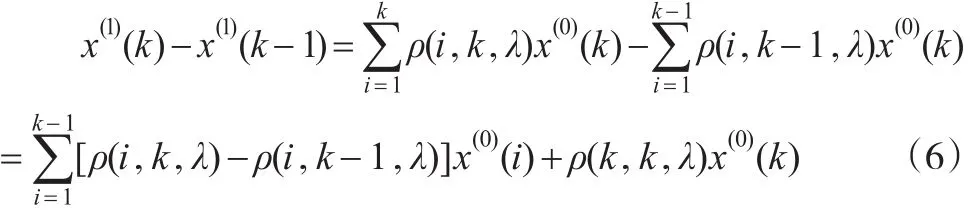
由于ρ(i,k,λ)是自定義函數，可以定義ρ(i,k,λ)＞0且是k的增函數。

證畢。

定理2：加權或變權算子與原序列規律不一致性。

證明：假如有一等比算子X(0)=(aq,aq2,aq3,…,aqn)

若一變權ρ=(λ1,λ2,…,λn)，必有λ1,λ2,…,λn不全部為0或1。

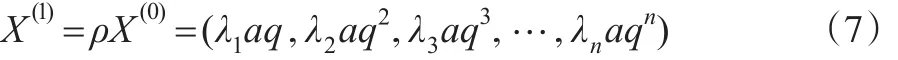
由于λ1,λ2,…,λn不能全部為0或1。所以式(7)就不是等比算子。

證畢。

從定理2中可知，通過加權或變權，可以對原序列進行修正，使新算子更符合某種數列規律。同時也可以對原序列中某個偏差較大的數進行修正。

定義4：設X(0)=(x(0)(1),x(0)(1),…,x(0)(n)，X(1)=(x(1)(1),x(1)(1),…,x(1)(n)是X(0)的加權或變權AGO，則

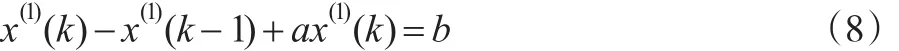
為GM(1,1,λ)模型的原始形式。

1.我們為了活命吃東西，為了保命又不敢吃東西；2.交話費的時候，才發現自己的廢話那么值錢；3.世界上最遙遠的距離，就是星期一上午到星期五下午；4.婚姻是愛情的墳墓，更可悲的是，小三還要來盜墓。

（1）若是加權，由式（1）和式（8）可得：

如果是非加權累計算子，則ρ(k)=1，則式（9）就為式（1）。因此，加權累加算子是原型是非加權累加算子的一般形式。

（2）若是變權，由式（1）和式（8）可得：

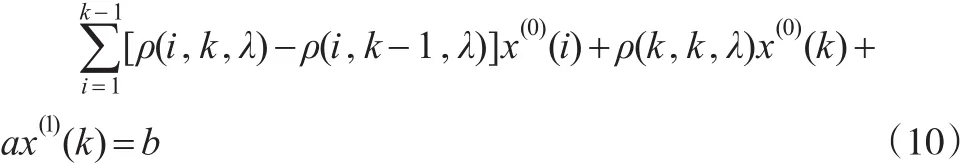
從式（10）可知，變權又是加權的一般形式。

由式（6）可得變權1-IAGO公式：

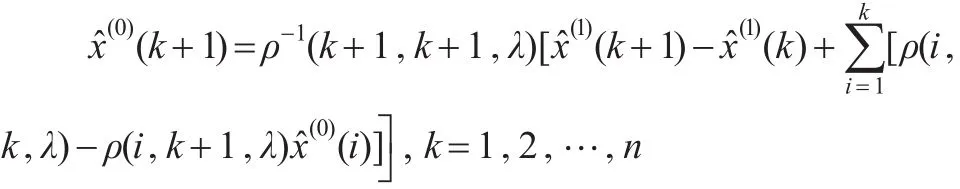
2 變權一次累加生成GM(1,1,λ)模型[11]

2.1 變權GM(1,1,λ)模型基本形式

定義5：設原始非負序列為X(0)=(x(0)(1),x(0)(2),…,x(0)(n)，其變權累加生成算子為，其中ρ(i,k,λ)是變權函數，其中，λ為變權因子。則稱：

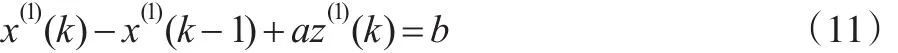
為GM(1,1,λ)模型的基本形式。

其中：

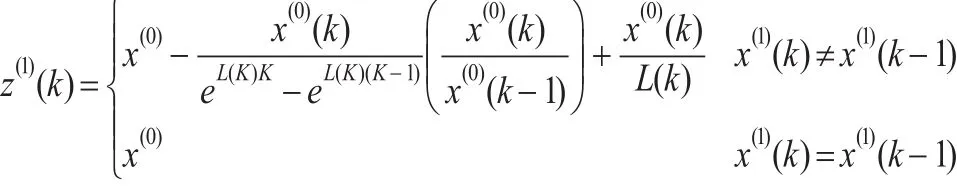
用最小二乘法估計式（11）參數，得：

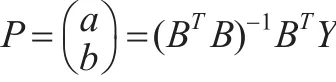
其中：

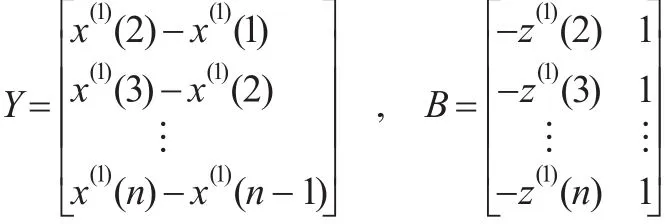
2.2 變權GM(1,1,λ)白化方程

由式（11）可得白化方程：

故上式的解：

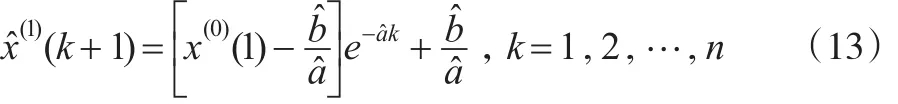
考慮初始條件對式（13）影響，假設：

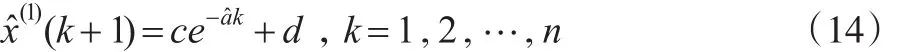
用最小二乘法對式（14）參數估計，則：

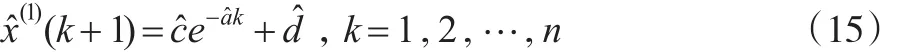
其中：

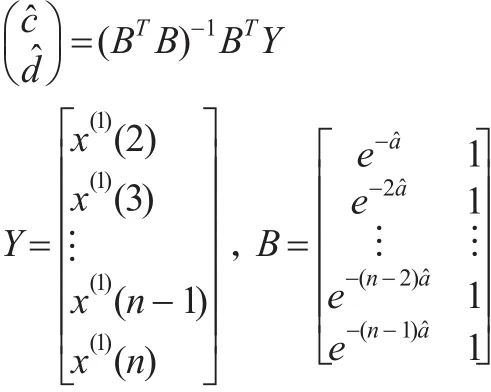
2.3 變權1-IAGO公式

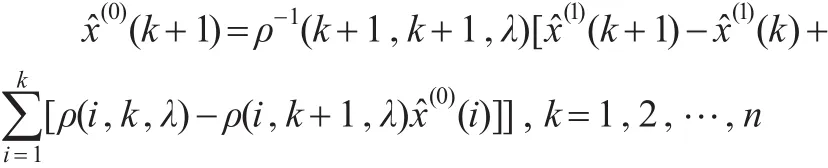
3 應用

取某省技術創新2010—1015年相關數據，對上述模型進行實證。

3.1 變權函數[13]

自定義變權函數為：

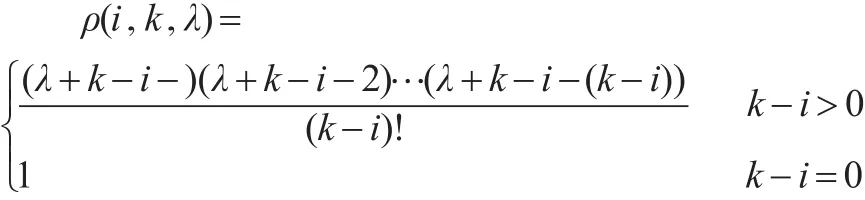
3.2 數據擬合與λ模型選擇

利用2010—2015年科研成果數據，選擇不同的λ值，得不同λ值下本模型的預測值和MAPE值，如表1所示。

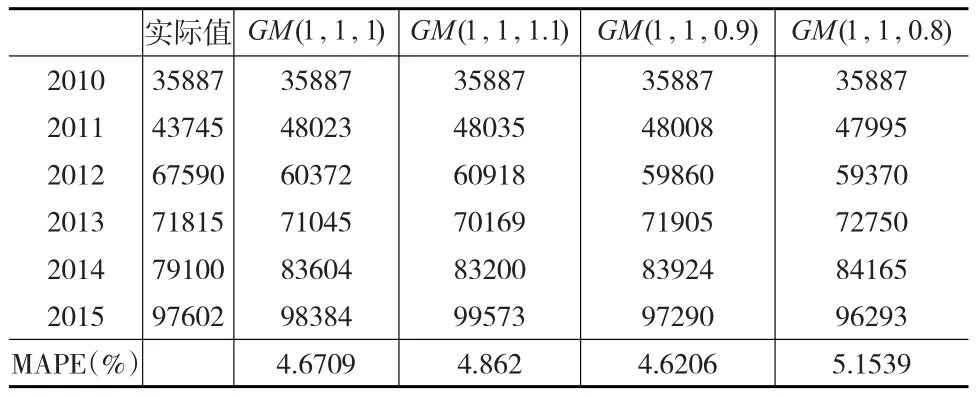
表1 某省科研成果量（項）

從表1知λ=0.9時，MAPE=4.6206%值最小，所以選λ=0.9時模型進行預測。

利用2010—2015年三種專利授權量，選擇不同的λ值，由模型預測出各年的預測值并得到不同模型的MAPE值，如表2所示。

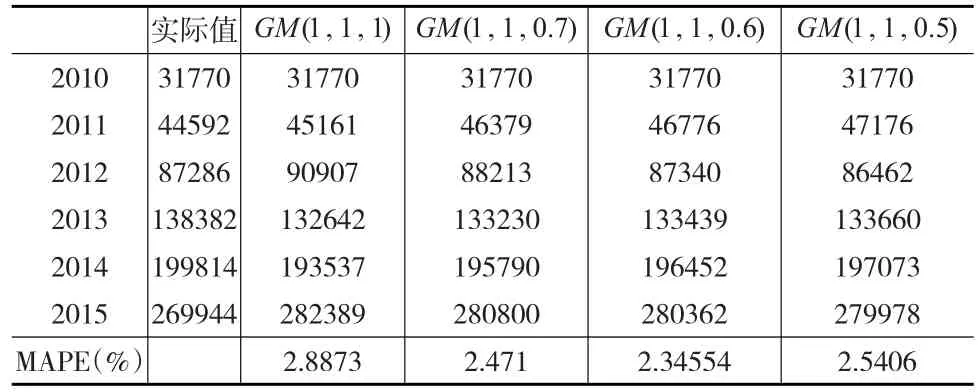
表2 某省三種專利授權量（件）

從表2中可知，MAPE=2.34554%最小，故取λ=0.6時模型進行預測。

利用2010—2015年大中型工業企業新產品銷售收入，選擇不同的λ值，由模型預測出各年的預測值并得到不同模型的MAPE值，如表3所示。

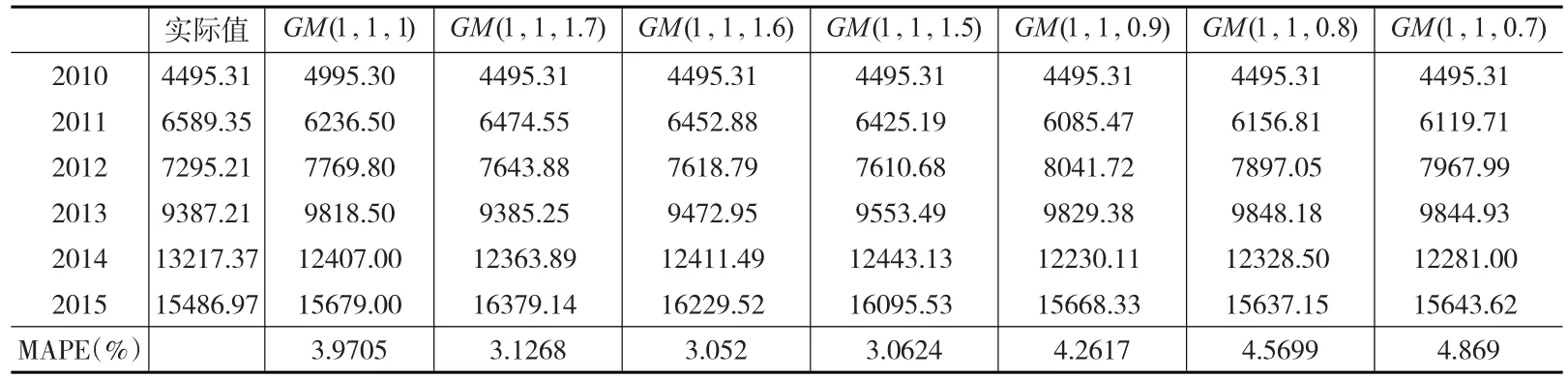
表3 某省大中型工業企業新產品銷售收入（億元）

從表3可以看出，λ=1.7,MAPE值最小，但這里取的舊數據權重較大，不符合新信息優先原則。本例中，λ越大,MAPE值就會增大。綜合考慮，取λ=1時模型預測。

利用2010—2015年高新技術產業產值，選擇不同的λ值，由模型預測出各年的預測值并得到不同模型的MAPE值，如表4所示。

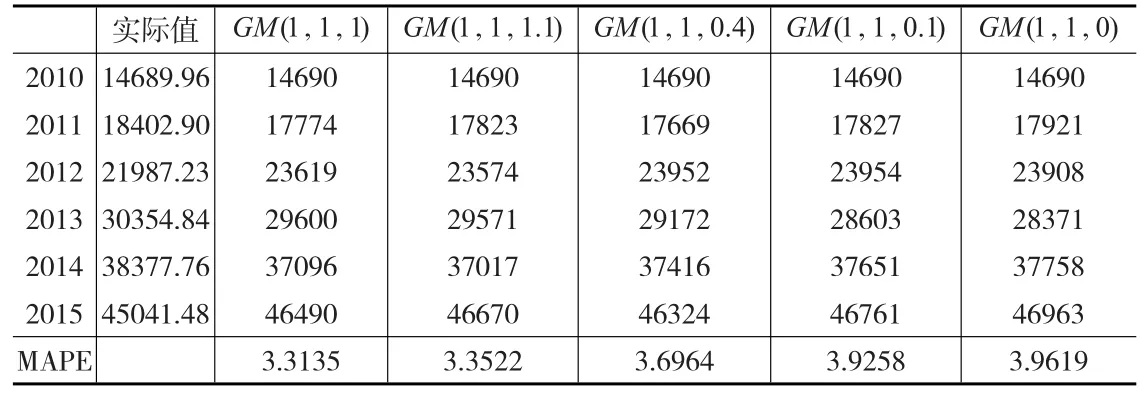
表4 某省高新技術產業產值（億元）

從表4中可知λ=1,MAPE=3.3135%,MAPE值最小；在新數據中，λ=0.4,MAPE=3.6964%，其值與最小值相差較小。考慮新信息優先原則和MAPE值大小，在此選擇λ=0.4時模型預測比較合理。

3.3 未來三年預測

由表1可知取λ=0.9時，根據2010—2015年數據可預測未來三年科研成果量，如表5所示。

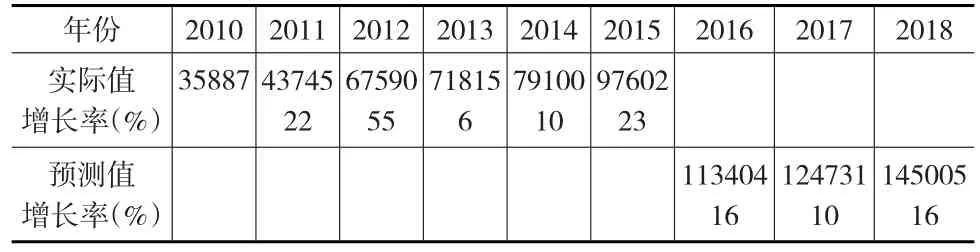
表5 某省科研成果量預測(項)

從表5可知，2010—2015年實際值數據波動很大，增長率6%～55%，顯然序列不符合平滑性和準指數關系，但取λ=0.9（見表1），經過變權因子的調整，使其預測增長率趨于平穩，并保持11%左右合理的增長率。

由表2可知取λ=0.6時，根據2010—2015年數據可預測未來三年專利授權量，如表6所示。

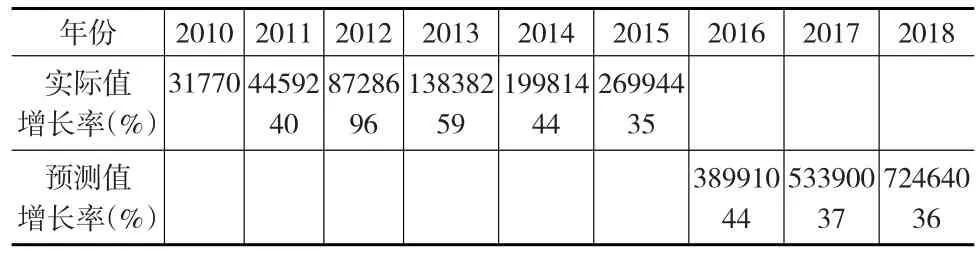
表6 某省三種專利授權量預測（件）

從表6可知，2010—2015年三種專利增長45%左右，一度達到96%，但取λ=0.6（見表2），經過變權因子的調整，使其預測增長平穩保持在35%左右，與前六年增長率相比，更合理、更平穩。

由表3可知取λ=1時，根據2010—2015年數據可預測未來三年大中型工業企業新產品銷售收入，如表7所示。

從表7知，2010—2015年增長率實際值數據波動很大，增長率從11%～47%,但選用λ=1（見表3）,以及采用新數據優先的新成代謝法，最后預測結果平穩增長在28%左右，這是比較合理的。

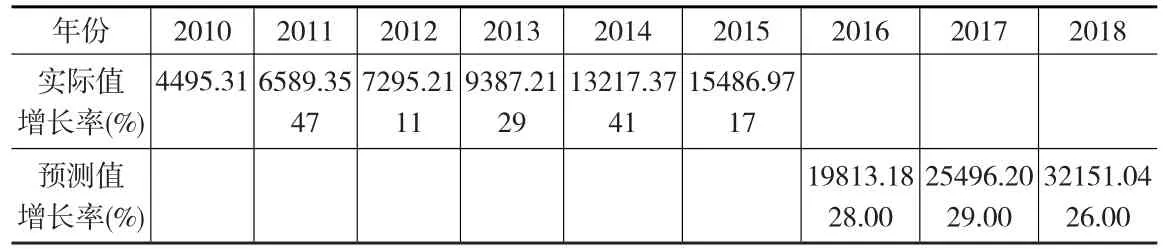
表7 某省大中型工業企業新產品銷售收入預測（億元）

由表4可知λ=0.4時，根據2010—2015年數據可預測未來三年高新技術產業產值，如表8所示。

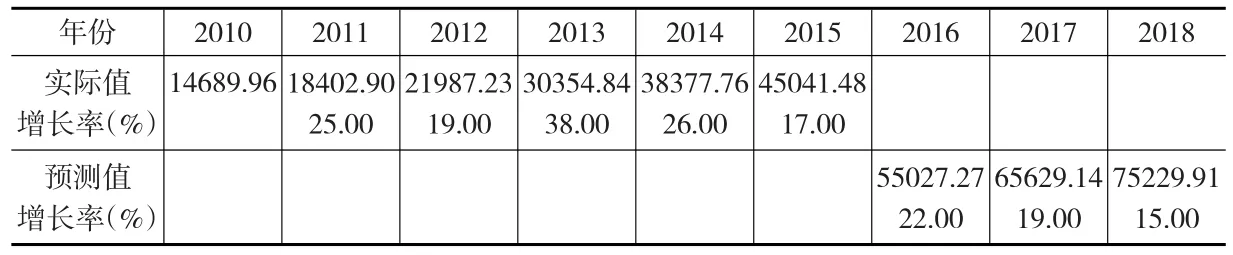
表8 某省高新技術產業產值（億元）預測

從表8可知，2010—2015年增長還是有一些波動，從2013年38%,分別下降到2014年的26%和2015年17%。在MAPE允許范圍內，考慮新數據優先，取λ=0.4（見表4），經過變權因子的調整，使其預測增長率平穩保持在19%左右，與前六年增長率相比，更合理、更平穩。

4 結束語

（1）變權GM(1,1,λ)模型是GM(1,1)一般形式。基于MAPE視角GM(1,1,λ)模型是否比GM(1,1)優越，取決于其處理的數據。通過選擇λ值，可以找到MAPE最小值。

（2）通過MATLAB計算可以發現，取λ小一點的值，最后一個擬合值與最后一個實際值誤差就小；反之，就大。這也說明應選擇λ小一點的值，確保預測值合理與準確。

（3）最小值的MAPE模型，其預測結果未必合理與準確。因此，選擇預測模型應從MAPE和新數據優先二方面綜合考慮。在MAPE允許范圍中，盡可能選擇較小一點的λ值，加大新數據權重，以保證預測的合理性與準確性。

[1]鄧聚龍.灰色系統理論教程[M].武漢:華中科技大學出版，1992.

[2]黨耀國.x(1)(n)為初值條件的GM模型[J].中國管理科學,2003,13(1).

[3]Wang Y H,Dang Y G,et al.An Approach to Increase Prediction of GM(1,1)Model Based on Optimization of the Initial Condition[J].Expert Syst Appl 2010,37(8).

[4]Liu S F.The Three Axioms of Buffer Operator and Their Application[J].The Journal of Grey System,1991,(3).

[5]王正新,黨耀國,劉思峰.變權緩沖算子及其作用強度的研究[J].控制與決策,2009,(8).

[6]譚冠軍.GM(1,1)模型的背景值構造方法和應用(Ⅰ)[J].系統工程理論與實踐,2000,(4).

[7]李星毅，李奎等.背景值優化的GM(1,1)預測模型及應用[J].電子科技大學學報，2011，40(6).

[8]周偉，方志耕，劉思峰.基于級比優化的廣義GM(1,1)預測模型[J].系統理論與實踐,2010,(8).

[9]姚天祥,劉思峰.離散GM(1,l)模型的特性與優化[J].系統工程理論與實踐,2009,29(3).

[10]Xie N M,Liu S F.Discrete Grey Forecasting Model and Its Optimization[J].Applied Mathematical Modeling,2009,(33).

[11]錢吳永，黨耀國，王葉梅.加權累加生成的GM(1,1)模型研究及其應用[J].數學的實踐與認識，2009,39(15).

[12]喬正明.基于粒子算法的變權累加生成的GM(1,1)模型[J].數學的實踐與認識,2011,41(1).

[13]Wu L F,Liu S F.Grey System Model With the Fractional Order Accumlation[J].Commun Nonlinear Sci Numer Simulat,2013,(18).

[14]Xiao X P,Guo H,Mao S H.The Modeling Mechanism,Extension and Optimization of Grey GM(1,1)Model[J].Applied Mathematical Modelling,2013,(38)