新建住宅虛擬重復交易數據的生成方法

劉 宇，蘇 攀，金升平

（武漢理工大學 理學院，武漢 430070）

0 引言

房地產的最大特點就是異質性。科學的房價指數編制模型，必須考察同質房產的價格變化，剝離品質變化對銷售成交價格的影響。國外房價指數的編制方法在經歷以中位數和簡單加權平均為代表的第一代方法、以樣本匹配法和拉氏加權為代表的第二代方法之后，建立在現代數理統計分析基礎上的第三代房價指數編制方法為同質性房價指數，其主要模型與方法有兩個：一個是特征價格法，直接把房子價格和一系列主要品質聯系起來。另一個是重復交易法,考察同一棟房子不同時期的成交價格變動[1,2]。

近年來，我國房地產價格明顯上漲，相關房價統計數據卻與大眾普遍的感知存在較大偏離，這暴露出房地產價格指數編制在反映房地產市場價格水平變化程度方面的缺陷。目前我國新建住宅房價格指數大多采用簡單的平均法、中位數法或加權平均法，只相當于國外的第一代和第二代方法，無法滿足同質可比的要求，在準確性等方面存在明顯不足。這就需要結合我國新建商品住宅的特點，運用國外的先進方法進行房價指數的編制方法研究。

房價指數的特征價格法，在理論上和學術界相對占有優勢，但在實際應用上有一定的困難，因為較為全面地收集每套住宅的特征數據的準確性難以保證，且代價很大。因此特征價格法不能很好地適用于我國新建住宅的房價指數的編制。長期以來，學術界認為，我國新建商品房只有一次交易，新建住宅的房價指數的編制不能應用重復交易法。但中國房地產有其特點，除少量原有的獨立自建房和別墅外，新建住宅都是樓宇結構且一個小區一個樓盤的成片開發。出于樓宇穩定性需要，樓宇除頂層之外其他樓層的戶型配比是一樣的，各種戶型在朝向位置上是一致的，樓上樓下同樣位置對應的戶型都是相同的[3]。從直觀上講，我國新建商品化住房結構較為單一或者說較“同質”。

國內有少數文獻對這一特點進行了研究[3-8]，本文將在先倚懿等[5]和Jin W H等[6]提出的基于上下樓集合的虛擬重復交易的基礎上，利用上下樓的關系和很多不同上下樓集合對應樓層價格基本相同的現象，研究不同上下樓集合可匹配的方法，以及兩種方法產生虛擬交易數據的融合問題。

1 虛擬交易數據產生方法模型

1.1 基于同一上下集合的虛擬數據產生方法

約定同一樓棟、同一單元、同一朝向的所有房屋為一個“上下樓集合”，一個單元一般由兩個上下樓集合構成，也有部分單元由三個或更多個上下樓集合構成。在同一年同一個月內同一上下樓集合售出了兩層，記為l1,l2( )l1＜l2，單價分別為p1,p2，記該月為t。而且從已有銷售記錄來看，這個朝向的所有樓層的總面積都相等。如果另外一個月此上下樓集合的房產售出了位于第l層，l層與l1和l2滿足一定的鄰近條件時，可以通過插值的方法計算出在第t月位于第l層房產的虛擬單價。

作為推廣，設同一上下樓集合房產在同一年同一個月內售出了k層，記為l1＜l2＜…＜lk，單價分別為p1,p2,…,pk，記該月為t。如果另外一個月上下樓集合房產售出了位于第l層。樓棟為高層或小高層，如總樓（記為ltotal）必須至少為12層。l1≥3,lk＜ltotal。當l層與所售出的k層中的兩層滿足一定的鄰近條件時，可用插值的方法計算出在第t月位于第l層房產的虛擬單價。用方法生成的虛擬交易數據稱為基于樓層的虛擬交易數據。

1.2 基于上下樓集合的虛擬數據產生方法

1.2.1 規則1基于同一樓棟不同上下樓集合的匹配規則設A和B為同一樓棟的不同上下樓集合，其總高度都為n，房產從第1層到第n層分別為A1,A2,…,An和B1,B2,…,Bn，設樓層集合，在同一年同一個月售出了方位A和B的第lk層，但不同樓層銷售的年月可以不同(k=1,2,…,s)。Al1,Al2,…,Als和Bl1,Bl2,…,Bls的銷售單價分別為pl1,pl2,…,pls和ql1,

如果滿足以下3個條件：

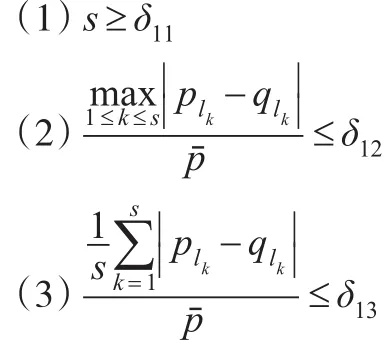
則稱兩個上下樓集合A和B是匹配的。其中δ11,δ12,δ13的設置視具體情況而定，例如δ11=4,δ12=0.04,δ13=0.02。

如果兩個上下樓集合A和B是可匹配的，則上下樓集合A的第i層房產Ai在某年某月的售價為pi，但Bi在該年該月沒有銷售記錄，則Bi在Ai對應的年和對應月的虛擬售價為pi。同理，如果Bi在某年某月的售價為pi，但Ai在這個對應的年和月沒有交易，則Ai在這個對應的年月的虛擬售價為pi。

1.2.2 規則2基于同一樓棟不同上下樓集合的匹配規則的改進

規則1中要求檢查匹配時，相同樓層都是同年同月銷售的。但有時相同樓層是相鄰月份銷售的，但相隔的時間不長。設A和B為同一樓棟的不同上下樓集合，其總高度都為n，房產從第1層到第n層分別為A1,A2,…,An和B1,B2,…,Bn，設樓層集合，在同一年同一個月或相鄰的月售出了上下樓集合A和B的第lk層，但不同樓層銷售的年月可以不同如果上下樓集合A和B的第li層為同一年或相鄰的月售出的，要求它們銷售日期相差的天數小于31天。設Al1,Al2,…,Als和Bl1,Bl2,…,Bls的銷售單價分別為pl1,pl2,…,pls和ql1,ql2,…,qls，Alk和Blk銷售日期相差的天數記為dk,k=1,…,s，再記

如果滿足以下3個條件：

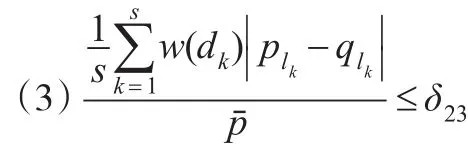
其中w(dk)為房價關于天數的權系數，可取w(d)=1-d/300,(0≤d≤30)。則稱兩個上下樓集合A和B是匹配的。其中δ21,δ22,δ23的設置視具體情況而定，例如δ21=4,δ22=0.04,δ23=0.02 。

與規則2一樣，如果兩個上下樓集合A和B是可匹配的，則上下樓集合A的第i層房產Ai在某年某月的售價為pi，但Bi在該年該月沒有銷售記錄，則Bi在Ai對應的年和對應月的虛擬售價為pi。同理，如果Bi在某年某月的售價為pi，但Ai在這個對應的年和月沒有交易，則Ai在這個對應的年月的虛擬售價為pi。

1.2.3 規則3基于不同樓棟的兩個上下樓集合的匹配規則

設兩個上下樓集合位于不同的樓棟，但這兩個樓棟屬于同一小區的同期樓盤，其總高度（總樓層）相同，也可仿照規則1或規則2，類似給出兩個方位是可匹配的定義。但對于相應參數的設置應相對苛刻一些。

1.3 兩種虛擬交易數據的融合及虛擬數據的處理

對于高層或小高層，可分別利用基于同一上下樓集合的虛擬交易數據模型（記為模型1）和基于不同上下樓集合的虛擬交易數據模型（記為模型2）生成虛擬交易數據，所以就存在兩個虛擬交易數據的融合問題。具體方法如下：可將模型1產生的虛擬數據再基于模型2產生虛擬數據，反過來亦可。如果一套房產存在相同時間產生了多條虛擬交易數據記錄，則將這幾條記錄合并成一條的虛擬交易數據。合并時交易價格可采用簡單平均或加權平均，其不同數據類型的權系數進行具體數據測算后確定。

2 虛擬重復交易數據產生方法的對比分析

2.1 虛擬交易數據示例

下面以湖北省襄陽市2012年1月至12月的83個樓盤的房地產的商業銀行按揭房貸數據為例，比較本文方法與前期的方法所產生數據質量問題。數據來源于中國人民銀行武漢分行，每套房產數據其中包括項目名稱、所在小區、樓棟、單元、樓層、房號，房產總價、房產面積、房產購買時間、房產交易單位價格、房產所在區域編號等信息。數據幾乎包括了襄陽市的所有樓盤，并且信息全面，能夠反映出襄陽市的房價指數變化情況。

在剔除內容不完整的信息后，獲得6354條有效樣本。首先根據基于同一上下樓集合的匹配規則產生虛擬數據1，產生虛擬交易數據4475條，與原始數據匹配共得到986條虛擬重復交易的數據。然后根據基于不同上下樓集合的匹配規則生成虛擬數據2，產生虛擬交易數據576條，與原始數據相匹配共得到285條虛擬重復交易的數據。對前兩種規則產生的數據進行融合，得到3862條虛擬交易數據，把原始數據與虛擬數據進行匹配找出同一房屋在不同時間虛擬重復售出兩次的交易對共有1178條。在考慮基于不同上下樓集合的匹配之后，多產生了384條重復交易數據。產生的數據形式如表1所示，這里只列舉小部分樓盤的部分變量的數據。

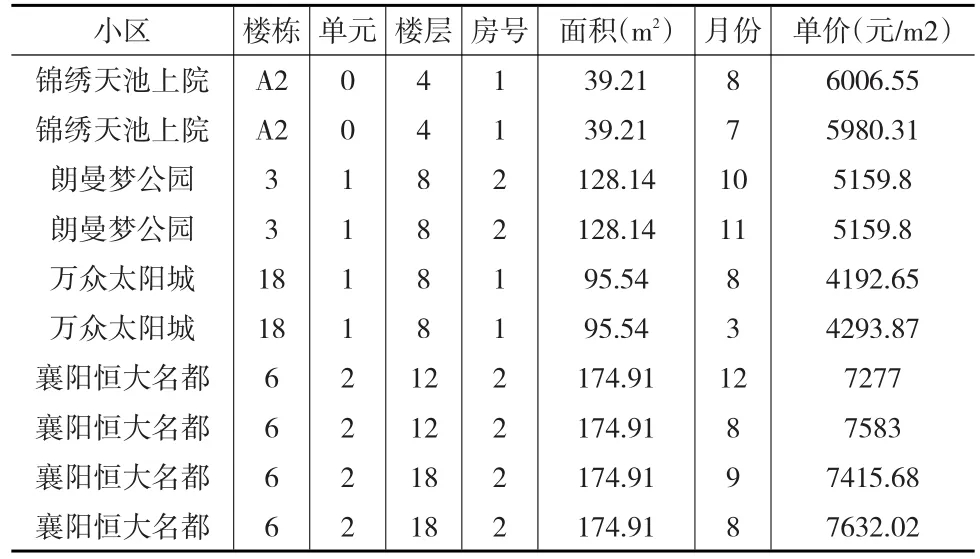
表1 虛擬重復交易數據

2.2 模型選擇

重復售出模型[2]的具體形式為：

其中Pi,t是第i套房產在時期t的交易價格。t是第1次交易時期而t'是第2次交易時期，滿足t'＞t。It是房產在時期t的價格指數，Uitt'是交易誤差，滿足，這里iid表示獨立同分布。式（1）取對數得：

其中pi,t=logPi,t,βt=logIt,uitt'=logUitt'

類似于重復交易模型，Case和Shiller[7]假定式（2）有另外的誤差結構：

這里t'＞t，Hi,t是一個Guassian隨機游走（random walk）過程，所以

Case和Shiller的三階段廣義最小二乘法（3GLS）如下：

（1）對式（2）運用OLS進行擬合。得出的結果為重復交易指數。記一對重復交易的殘差為εitt'。

（2）對以下關于α0,α1回歸問題運用OLS進行擬合：

其擬合值記為'，組成矩陣

對式（2）運用加權最小二乘法進行擬合，其加權矩陣為W-1。可以看到，加權后，對數交易誤差為常數，不在存在異方差，因此，對于參數估計量，可以得到最優的估計量。因此本文可以運用加權重復交易法估計房地產價格指數：

Case&Shiller的三階段廣義最小二乘法被稱為加權重復交易模型，對重復交易模型誤差項的異方差問題進行處理，得到的估計量更優，被廣泛應用在住房金融研究中。本文選用Case&Shiller模型對兩種方法產生的虛擬重復交易數據進行對比研究。

2.3 結果對比分析

把基于同一上下樓集合的虛擬重復交易數據方法記為方法1，把本文提出的虛擬重復交易數據產生方法記為方法2。運用Case&Shiller模型計算出兩種產生虛擬重復交易數據的方法所得到的各月份的房價指數如表2所示。

表2 方法1和方法2所得各個月份的房價指數 （單位：%）

由表2可以看出，兩種方法所得的房價指數的變化趨勢大致相同，相同月份的房價指數相差不是很大，誤差的最大值為0.18。方法2所產生的虛擬重復交易數據與方法1產生的虛擬重復交易數據質量相當，方法2產生的數據樣本量較大。兩種方法編制的房價指數如圖1所示。

圖1 房價指數變化圖

由圖1可知，指數1代表是基于方法1所得的房價指數變化曲線，指數2是基于方法2產生的房價指數變化曲線。總體來看，房價指數在不斷增大與我國房價不斷上漲的趨勢相吻合。兩條曲線的波動情況大體一致，但基于后者所得到的房價指數稍高于基于前者所產生的房價指數，波動性更大一點，這比較符合我國房價的變化情況。

圖2 Case&Shiller模型計算房價指數的殘差圖

圖2給出Case&Shiller模型計算房價指數的殘差圖，可以看出除個別異常點之外大部分殘差都在[-2，2]之間圍繞0上下波動，說明模型的擬合效果較好。可以在某些程度上認為，本文選擇的虛擬重復交易模型符合我國新建住宅的市場情況，在一定程度上反映房價指數的變化。

3 結論

在房地產價格指數編制模型的構造過程中，數據的質量和數據的容量是編制房地產價格指數的關鍵性因素。如何獲得足夠的數據和可行性高的數據，是編制房價指數時必須解決的重要理論問題。本文分別基于同一上下樓集合和不同上下樓集合的虛擬交易數據產生方法來產生虛擬交易數據，并考慮到對兩種數據的融合，增大了樣本容量，提高了數據的質量。將虛擬交易數據與原樣本進行配對，得到虛擬重復交易數據，滿足重復交易法的數據形式，可行性高。通過運用優化的重復交易模型Case&Shiller模型對房價指數的計算以及對殘差的分析，可以認為利用虛擬重復交易數據，可以更為科學地編制我國新建住宅房價指數，更為準確地反映我國房價市場的價格變化趨勢，本文的方法達到了國際上第3代房價指數方法的標準。

[1]楊楠.房價指數的編制、管理與應用[M].上海：上海財經大學出版社，2010.

[2]Bailey M J,Muth R F,Nourse H O.A Regression Method for Real Estate Price Index Construction[J].Journal of the American Statistical Association,1963,58(304).

[3]許永洪.住房體格指數編制理論與應用研究[M].北京：中國社會科學出版社，2013.

[4]Guo X Y,Zheng S Q,Geltner D,et al.A New Approach for Constructing Home Price Indices:The Pseudo Repeat Sales Model and Its Application in China[J].Journal of Housing Economics,2014,(25).

[5]先倚懿，金升平.混合效應模型在新建住宅房價指數中的應用研究[J].統計與決策,2016,(15).

[6]Jin W H,Jin S P.The Virtual Repeat Sale Model for the House Price Index for New Building in China[J].Applied Mathematics,2014,5(22).

[7]Case K E,Shiller R J.The Efficiency of the Market for Single-Family Homes[J].American Economic Review,1989,79(1).

[8]金升平,曾恂,李瓊.中國新建普通商品房價格指數編制方法研究[J].武漢金融，2017,(6).