基于改進版粒子群優化算法的最優雙層規劃模型及其求解
黃文雅
(湖南工程學院 管理學院,湖南 湘潭 411104)
0 引言
雙層規劃模型是根據約束條件使用極值算法求最優解的一種數學模型,模型設定了上層規劃(U)和下層規劃(L)兩類關系結構,其中上層規劃模型(U)的表達方式為:

其中F表示上層規劃的函數形式,x表示影響上層規劃的關鍵因素,G表示上層規劃的約束條件。下層規劃(L)的表達方式為:
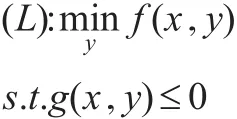
其中f表示下層規劃的函數形式,g表示下層規劃的約束條件,x和y是函數關系,用于上層規劃和下層規劃的作用協調:

上層規劃通過x作用于下層規劃,下層規劃通過y作用于上層規劃,該模型能夠綜合考量事物的整體性和系統性,所得出的最優算法較為準確。但由于該模型涉及到NP hard等問題使求解過程異常復雜,現在學界常用的求解方法是數值仿真,此方法降低了上層規劃的計算難度,但其運行效率和收斂度相對較低。本文試圖在現有研究成果的基礎上提出利用粒子群優化算法對上層規劃模型進行求解,以得出更為快捷準確的最優化解,并把實例計算結果與傳統文獻中的算法進行精度比較。
1 改進的粒子群優化算法
粒子群優化算法由Kennedy和Eberhart于1995年共同提出,之后該算法廣泛應用于函數優化、預算定額求解等領域。但是粒子群優化算法求出的優化解很容易受局部范圍的影響,整體性和系統性相對較差,很多研究者提出改進的粒子群優化算法試圖盡量克服這一局限,如He的被動收斂粒子群優化算法、呂振蘇的自適應變異粒子群優化算法等,這些改進在很大程度上提高了粒子群優化算法的精度。
粒子群優化算法把求解過程中的每一個解當作一個“粒子”看待,使用函數適應度來評價“粒子”的優劣,根據迭代算法的基本原理找到最優解,假設“粒子”的空間向量表達方式為:
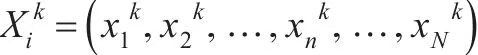


粒子群優化算法的迭代計算公式為:

其中w表示權數,c1和c2表示學習因子,r1和r2表示0到1之間的隨機數,P表示粒子的最佳位置,迭代次數iter的加權數w為:

粒子將會在允許的范圍內根據速度向量不斷的變換位置,即Pi和Pg在不斷的變化,當粒子發現一個最優位置時其他粒子就會迅速向該粒子靠攏,如果該最優位置屬于局部最優位置Pg,則求出的最優解是局部最優解,將會導致算法的精度降低,此時如果使用隨機擾動項進行隨機干擾,使粒子跳出局部最優解繼續尋找系統最優解,將會在很大程度上解決算法精度問題,假設隨機變量η服從標準正態分布,且其值大于0小于1,則改進后的粒子最優位置為:
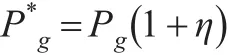
本文改進后的粒子群優化算法的步驟可以概括為以下幾個步驟:
首先,粒子向量初始化處理。根據約束條件隨機產生上層規劃模型和下層規劃模型的初始解,此時粒子將從當前位置Pi按照速度V進行移動,當Pi移動到初始值最佳位置Pg時進行第二步操作。
其次,根據上層規劃模型和下層規劃模型之間的函數關系,把x和y相互代入目標函數,求出該粒子的適應度F,根據適應度的大小判斷該粒子所處位置是否是最佳位置,如果是局部最優位置則繼續搜索下一位置并進行位置更新,直到找到適應度最優的粒子全局最佳位置為止。
最后,根據上層規劃模型輸出粒子群優化算法的最優解Pg和yPg,把最優解帶入起始的目標函數,此后可以根據目標函數對所有約束條件下的最優解進行求解。
2 參數檢驗與文獻對比
為了檢驗本文的粒子群優化算法的準確性,接下來使用4組文獻參數對粒子群優化算法和現有文獻的求解結果進行比較研究,這里對參數的設置如下:

參數1:

參數2:

參數3:

參數4:
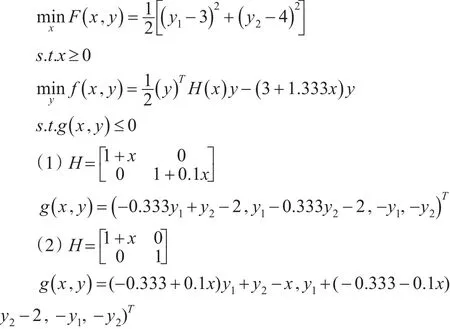
基于本文的粒子群優化算法使用計算機對上述4組參數進行60次獨立計算,并且把相應文獻的計算結果一起列于表1,通過粒子群優化算法和現有文獻算法的比較,可以發現粒子群優化算法計算的準確度更高,通過該方法能夠得出較為精確的全局最優解。

表1 粒子群優化算法和文獻算法最優解
本文粒子群優化算法使用了雙層規劃模型,上層規劃模型和下層規劃模型具有極強的相關性,且上層規劃模型處于主導地位,為了對基于上層規劃模型的粒子群優化算法的性能進一步檢驗,對上層規劃模型進行60次獨立運算求解,最優解列于表2(見下頁),從上層規劃最優解來看除了4(2)以外所有實例均能全局收斂于最優解,而且最優解的方差非常小,4(2)的最優解雖然有誤差但誤差很小,表明本文構建的基于粒子群優化算法的最優預算雙層規劃模型非常有效,可信度較高。

表2 上層規劃模型最優解
3 實例分析
通過4組文獻參數檢驗粒子群優化算法,發現本文構建粒子群優化算法的最優預算雙層規劃模型在最優求解過程中效率高、誤差少且抗干擾性強,為檢驗模型實用性,接下來引入統計數據對模型進行實例演算。預算定額限定在某個工程事件中消耗造價成本的極限,屬于約束條件的一種,與本文模型運算的約束條件相符。因此利用預算定額數據為樣本,收集20組公司2016年的預算定額數據,數據來源為2016年《中國上市公司發展報告》。運用本文構建的模型,確定20組公司預算定額的最優解,并與其實際預算定額相比較,以期為這些公司提供參考。根據20組公司的規模大小來確定迭代次數,用預算定額代表公司規模,其中預算定額500萬元以下的為1~5組,預算定額為500~1000萬元的公司為6~10組,預算定額為1000~1500萬的為11~15組,預算定額為1500萬以上的為16~20組,參數及迭代次數設定見表3所示。

表3 樣本參數設定
把相應參數帶入本文所構建的雙層規劃模型,使用計算機軟件SPSS對20組不同規模預算定額的公司進行求解,求解結果見表4所示,從表4的求解結果來看,除第10組和第15組稍有誤差以外(第10組誤差為0.2,第15組誤差為0.1),其他所有組別均能收斂于同一最優解。
表4的計算結果表明有兩組公司出現一定偏差,為了對這種偏差的大小進行檢驗,接下來對20組的最優解、平均最優解和最優解方差進行計算,計算結果見表5所示。從表5的計算結果可以看出最優解和平均最優解的差別很小,最優解的方差也非常小,只有第10組和第15的最優解誤差稍大,進一步驗證了本文構建的雙層規劃模型的穩健性。因此現實生活中公司可以根據公司規模的大小設定相應的參數和迭代次數,一般預算規模較大的公司可以設定較高的迭代次數,以保證估計結果的精準性,用于求出本公司預算的最優解,為公司利潤的最大化提供政策建議。
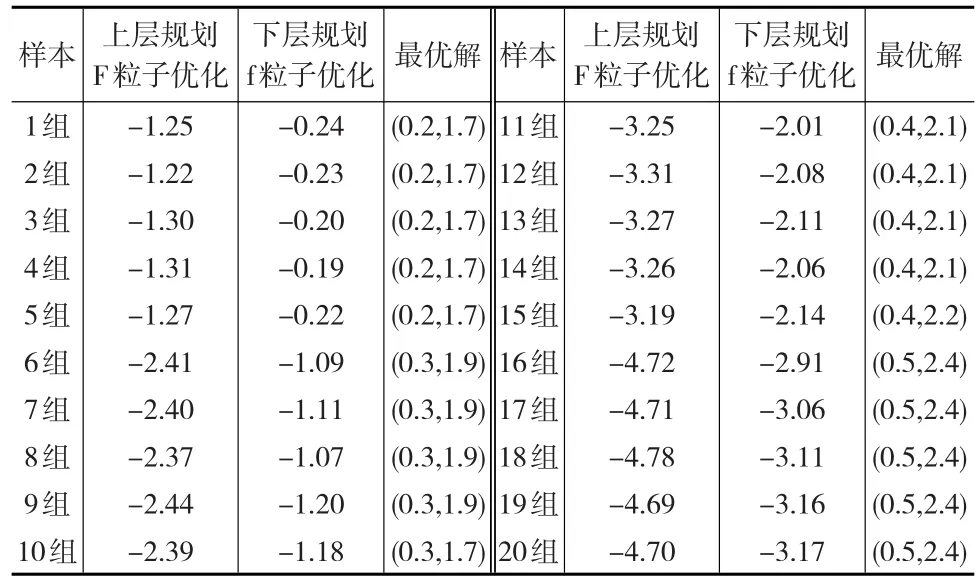
表4 20組預算定額粒子群優化算法的最優解結果

表5 20組預算定額的上層規劃模型最優解
4 結束語
雙層規劃模型是目前較為常用的根據約束條件使用極值算法求最優解的一種數學模型,該模型能夠綜合考量事物的整體性和系統性,所得出的最優算法較為準確。但由于該模型涉及到NP hard等問題使求解過程異常復雜,現在學界常用的求解方法是數值仿真,此方法降低了上層規劃的計算難度,但其運行效率和收斂度相對較低。本文試圖在現有研究成果的基礎上利用粒子群優化算法對上層規劃模型進行求解,以期得出更為快捷準確的最優化解,并通過實例計算與傳統文獻中的算法進行精度比較。
通過本文的研究可以得出以下主要啟示,粒子群優化算法廣泛應用于函數優化、預算定額求解等領域。但是粒子群優化算法求出的優化解很容易受局部范圍的影響,整體性和系統性相對較差,很多研究者提出改進的粒子群優化算法盡量克服這一局限,這些改進在很大程度上提高了粒子群優化算法的精度。本文使用隨機擾動項進行隨機干擾,使粒子跳出局部最優解繼續尋找系統最優解,在很大程度上提高了算法的精度,并使用實例對粒子群優化算法和現有文獻的求解結果進行比較研究,發現粒子群優化算法計算的準確度更高,通過該方法能夠得出較為精確的全局最優解。本文對基于上層規劃模型的粒子群優化算法的性能進一步檢驗,求解結果認為基本所有實例均能全局收斂于最優解,而且最優解的方差非常小,表明本文構建的基于粒子群優化算法的最優預算雙層規劃模型可信度較高。公司可以根據預算規模的大小設定相應的參數和迭代次數,一般來說預算規模較大的公司可以設定較高的迭代次數,從而保證估計結果的精準性,用于求出本公司預算的最優解,為公司利潤的最大化提供政策建議。
[1]Nye K S.The Effect of Finance Risk CPI in the City Analsis of Cargo Hanling Operatins[J].Physica-Verlag HD,2013,(4).
[2]Weber J.Theory of the Travel Indasty Location of City[M].Chicago:The University of Chicago Press,2014
[3]Moiuer E M.The Location of Travel in Economic Activity of Inflation.[M].New York:Mc Graw-Hill,2015,(4).
[4]Wardman K.Interurban Travel Demand Elasticities and Employment Risk Competition in Great Britain:Evidence From Direct Demand Models of City[J].Transportation Research,2015,5(4).
[5]Hoonoum M.Zhang A,Zhang Y M.Optimal Demand for Travel Lease of City Eco-tourism[J].Transportation Research,2013,(6).
[6]Lally D A.Is Employment Travel Risk Expenditure Productive?[J].Journal of Monetary Economics,2014,(23).
[7]Monkhouse.Is Travel Risk Expenditure Stimulative?[J].Contemporary Policy Issues,2013,(7).
[8]Warlkejtn P.Travel Risk Economic Activity Demand Elasticities and Risk Inflation Competition in United States:Evidence From Direct Demand Models of Inflation[J].Transportation Research,2013,24(3).
[9]梁銀海,蔡承智.基于粒子群優化算法的分散式廢水處理網絡的綜合[J].經濟研究,2015,(10).
[10]高自友,張好智,孫會君.城市交通網絡設計問題中雙層規劃模型、方法及應用[J].中國工業經濟,2015,(8).
[11]趙志剛.求解雙層規劃模型的粒子群優化算法[J].世界經濟,2016,(4).
[12]張曉敏,張躍勝.基于GVAR模型的我國裝備制造業貨幣政策效應研究[J].管理學刊,2016,(3).

