2×2型博弈決策均衡的歸一化解法

李停

（銅陵學院經濟學院，安徽銅陵244000）

0 引言

現實中生活中的企業決策，無論是產量、價格、廣告、研發都不再是孤立無關的，而是彼此間存在策略依存和策略互動。尤其是對生產日趨集中的寡占市場，企業任何行動都必須考慮其競爭對手的反應，傳統決策理論和運籌學方法很難解決這類利益相互影響的決策均衡問題。博弈論正是研究在利益相互影響的局勢中，局中人如何選擇自己的策略才能使自身的收益最大化的均衡問題[1]。近半個世紀以來，博弈論的理論和方法激起管理學家的極大興趣，將決策理論的發展推向前所未有的新高峰。納什均衡是博弈論最核心的概念，由于戰略管理本質上也是組織如何在相互影響的對局中尋求決策均衡的問題，所以本文不加區分地使用納什均衡和決策均衡的概念。

Nash（1950）[2]應用數學上的不動點定理，證明了“任何有限的策略型博弈至少存在一個混合納什均衡”。隨后，Debreu（1952）[3]給出了“在n個局中人的策略型博弈中，滿足局中人策略空間Si是歐式空間的非空有界閉集、支付函數Ui(s)連續且對Si是擬凹函數，該博弈存在一個純策略納什均衡”。這是博弈論學科發展過程中的兩大理論基石，解決了均衡的存在性問題。國內學者中，李正龍（2001）[4]、朱年磊等（2006）[5]對靜態博弈純策略納什均衡的存在性作了延伸性探討。但從實踐應用角度看，如何尋求納什均衡同樣不容忽視?，F有文獻大致可梳理出博弈均衡的三種求解方法：相對優勢劃線法、期望支付等值法和最優反應函數法。這些方法不同程度地存在適用范圍有限、過程繁瑣等弊端。如何尋求一種歸一化解法，將復雜的納什均衡求解過程“簡單化、程序化和規范化”，正是本文的寫作目的。本文將在理論上證明，局中人的支付矩陣在局部變換下不改變博弈的均衡特征，并以納什均衡不變性定理為基礎，完成16種類型的2×2型博弈決策均衡的歸一化求解。

1 2×2型博弈構成要素及均衡表述

1.1 2×2型博弈的構成要素

對于完全信息的靜態博弈，策略型博弈模型是較為適當的表示，而局中人、策略和支付是構成策略型博弈的三個基本要素。本文分析的2×2型博弈是指包含2個局中人，每個局中人只有2個策略的有限博弈。2×2型博弈構成要素雖然簡單，但卻是分析N個局中人復雜博弈的基礎。從純粹數學意義上講，這無非是2維向量空間向N維向量空間的形式化推廣。

于是G=(2,S1,S2,u1,u2)為2×2型博弈的策略型表示，S1、S2分別是局中人1、2的策略空間。在2×2型博弈中，S1、S2都只含有2個元素，記

令s1、s2是局中人1、2具體的某個策略，s1∈S1，s2∈S2。u1、u2代表局中人1、2在各種策略組合下的支付。由于局中人和策略都是有限集，2×2型博弈的策略組合也是有限集，策略組合空間可表示為

由于分析的是完全信息靜態博弈，策略等同于行動。記局中人1的行動集為α={α1,α2}，局中人2的行動集為β={β1,β2}。再記u1(αi,βj)=aij，u2(αi,βj)=bij，i=1,2，j=1,2。該2×2型博弈的支付矩陣如表1所示：為下文分析方便，記表示局中人1、2的支付矩陣。

表1 2×2型博弈的支付矩陣

1.2 2×2型博弈的均衡表述

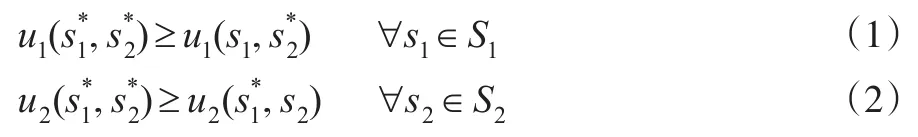
由于并非所有2×2型博弈都有純策略納什均衡，需引入混合納什均衡的概念。局中人1的混合策略X=[p,1-p]表示分別以概率p、1-p選擇行動α1、α2。局中人2的混合策略Y=[q,1-q]T表示分別以概率q、1-q選擇行動β1、β2。利用支付矩陣A和B，局中人1、2的期望支付的代數表示為E1(X,Y)=XAY、E2(X,Y)=XBY。這里X表示局中人1的混合策略行向量，Y表示局中人2的混合策略列向量?；旌喜呗?X*,Y*)為G的混合納什均衡，當且僅當X*AY*≥XAY*、X*BY*≥X*BY對任何X、Y同時成立。易知當p=1或p=0時，局中人1的混合策略e1=(1,0)、e2=(0,1)退化成純策略α1、α2；同樣，當q=1或q=0時，局中人2的混合策略e1=(1,0)、e2=(0,1)退化成純策略β1、β2。因而混合策略包含著純策略的含義，對二者的分析便可以統一起來。

2 納什均衡的不變性

2.1 納什均衡不變性定理

定理1：設G=(2,S1,S2,u1,u2)為某2×2型博弈，則納什均衡對任一局中人的支付函數的正仿射變換下不變。即對i∈{1,2}，令(s)=σiui(s)+εi，其中σi＞0。正仿射變換下的新2×2型博弈與G有相同的納什均衡。

定理2：納什均衡在支付函數的局部變換下不變。

2.2 納什均衡不變性定理的實質

定理1和定理2使用嚴謹而又晦澀的數學語言詮釋納什均衡的不變性。事實上，借助局中人支付矩陣A和B對該定理簡化，有助于把握納什均衡不變性定理的實質。

對G的支付函數作正仿射變換，相當于對局中人1、2的支付矩陣A、B的每個元素乘以一個正數再加上一個常數。即A′=σ1A+ε1，B′=σ2B+ε2，其中，σ1,σ2＞0，εi是元素取值為常數的2階方陣。

對G的支付函數作局部變換，相當于對A的某一列加一個常數，或者對B的某一行加一個常數。即或者

3 2×2型博弈的決策均衡

3.1 局中人支付矩陣的對角化

既然對支付函數的局部變換實質是對局中人支付矩陣的列或行加某個常數，那么一個自然的想法是只要常數選取得當，很容易將局中人的支付矩陣對角化。這將使得納什均衡求解過程得到簡化，以此為基礎可探討2×2型博弈決策均衡的歸一化解法，同時納什均衡不變性定理保證了這種探討的有效性。

對局中人1的支付矩陣A進行列變換，將其變成對角陣A′，具體過程如式（3）所示；對局中人2支付矩陣B進行行變換，將其變成對角陣B′，具體過程如式（4）所示：

由于任一2×2型博弈都可通過局部變換成對角陣，下文對其決策均衡的討論只需對支付矩陣是的2×2型博弈進行。

3.2 局中人的最優反應函數

3.2.1 局中人1的最優反應函數

局中人1的混合策略為X=(p,1-p)，局中人2的混合策略為Y=(q,1-q)T。局中人1的最優反應是對不同的Y，選擇X最大化期望支付E1(p,q)。

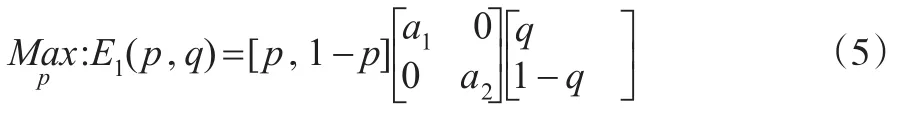
（1）a1＞0，a2＜0。當a1+a2＞0時，恒有此時，對?q∈[0,1]，p=1最大化期望支付E1；而當a1+a2＜0時，顯然成立，從而也得到綜合起來，局中人1的最優反應函數：p(q)=1，?q∈[0,1]。

（2）a1＜0，a2＞0。類似情形（1），可得到此時恒有，故局中人1的最優反應函數：p(q)=0，?q∈[0,1]。

（3）a1＞0，a2＞0。當時，恒成立。?p∈[0,1]，都能最大化期望支付E1；當時，，局中人1的最優反應是p(q)=0；當時，，局中人1的最優反應是p(q)=1。局中人1的反應函數可用分段函數表示：

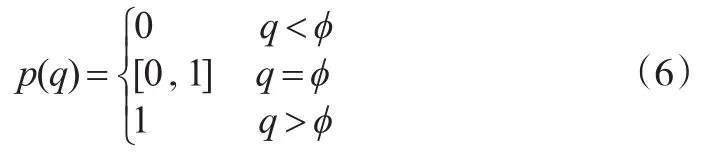
（4）a1＜0，a2＜0。類似情形（3），可得局中人1的最優反應函數：

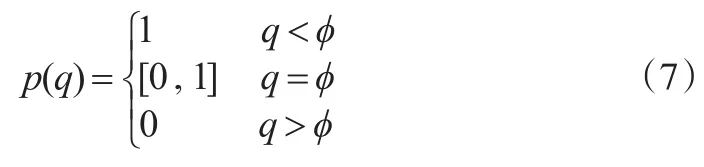
3.2.2 局中人2的最優反應函數

局中人2的最優反應是對不同的X，選擇Y最大化期望支付E2(p,q)。

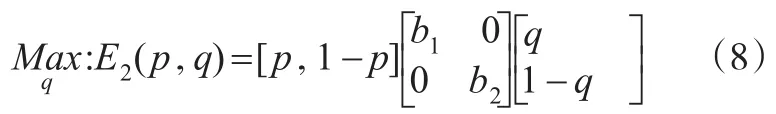
（1）b1＞0，b2＜0。局中人2的最優反應函數：q(p)=1，?p∈[0,1]。

（2）b1＜0，b2＞0。局中人2的最優反應函數：q(p)=0，?p∈[0,1]。

（3）b1＞0，b2＞0。局中人2的最優反應函數可用分段函數式（9）表示：

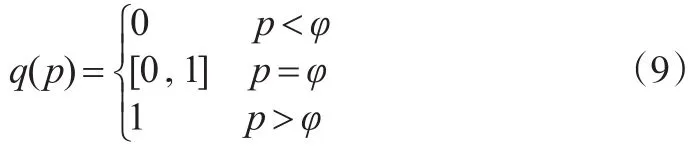
（4）b1＜0，b2＜0。局中人2的最優反應函數可用分段函數式（10）表示：

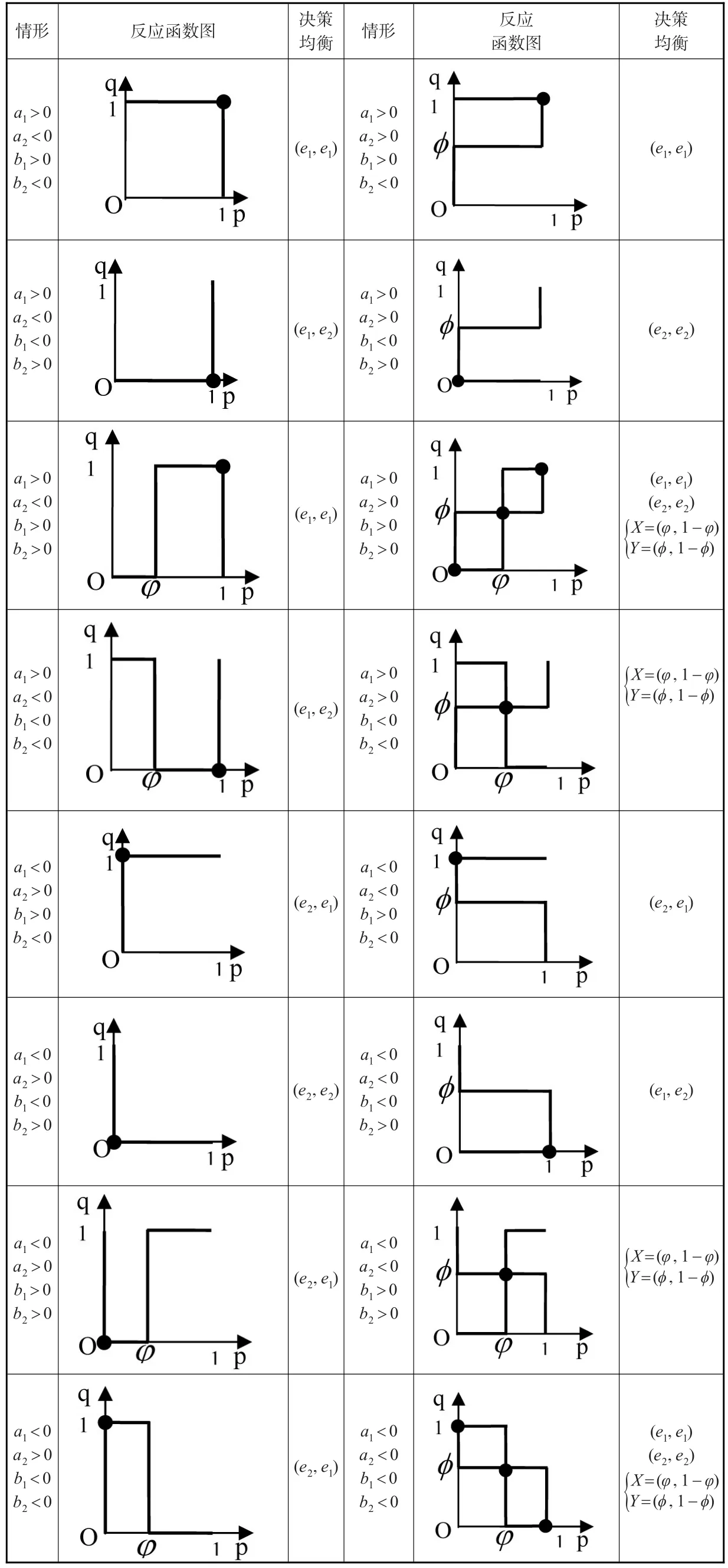
表2 2×2型博弈的決策均衡

3.3 決策均衡

由于局中人1和2的反應函數都有4種情形，交叉組合后共有4×4=16種情形。上頁表2列出2×2型博弈在每種情形下的反應函數圖形和決策均衡。表2中(ei,ej)是純策略納什均衡，如(e1,e2)表示[(1,0),(0,1)]，亦即純策略組合(α1,β2)。粗實線表示相應的反應函數曲線。

4 算例分析及方法比較

以企業管理中著名的“協調”博弈為例，闡述不同決策均衡求解過程并進行方法比較。企業1和企業2是相關行業內的兩個廠商，都具備生產產品甲和乙的技術條件。比較而言，廠商1在產品甲生產上有比較優勢，廠商2在產品乙生產上有比較優勢。但由于生產過程中的技術互補的原因，兩家企業生產同一種產品更容易獲得外部規模經濟。現在的問題是，兩家企業如何協調，實現產品選擇決策均衡。表3列出各種策略組合下的支付。

表3 產品選擇“協調”博弈

4.1 相對優勢劃線法

相對優勢劃線法的基本思想是：對每個局中人在對手各種確定的策略情形下尋求其最優策略，并在該局中人相應的支付下面劃一短線。等兩個局中人都分析完成后，每個局中人支付下面都有短線的策略組合就是納什均衡。

對于企業1而言，給定企業2選擇產品甲，選擇產品甲支付是3，選擇乙支付是-1，于是在(3,2)中局中人1的支付3下面劃線。類似這樣的討論對所有局中人的全部策略，劃線結果也在表3中同時給出。通過相對優勢劃線法，容易得到該產品選擇“協調”博弈的決策均衡是（產品甲，產品甲）、（產品乙，產品乙）。

相對優勢劃線法的優點是簡單易行，但只適用于純策略納什均衡的求解。

4.2 期望支付等值法

期望支付相等是混合納什均衡的一個重要性質。如果(X*,Y*)是博弈G的一個納什均衡，這里X=[p,1-p]表示局中人1以概率p、1-p選擇行動α1、α2，Y=[q,1-q]T表示分局中人2以概率q、1-q選擇行動β1、β2，那么E1(X*,Y*)=E1(X,Y*)、E2(X*,Y*)=E2(X*,Y)對任意X、Y都成立。給定某局中人選擇均衡策略，另一局中人無論選擇什么混合策略都不改變其支付。在混合納什均衡點上，局中人的期望支付與另一局中人的策略選擇無關。這當然也包括兩種純策略，由此引入求解2×2型博弈混合納什均衡的一種簡便方法——期望支付等值法。

仍以產品選擇“協調”博弈為例，說明期望支付等值法的求解過程。對于企業1而言，當企業2選擇混合策略(q,1-q)時，其選擇純策略產品甲和產品乙的期望支付相等，即：

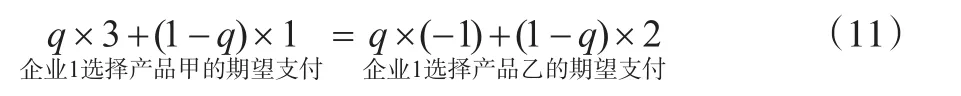
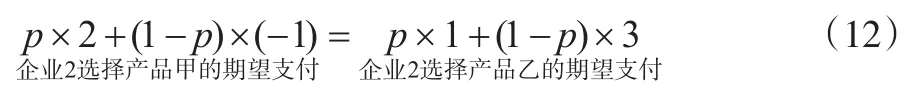
4.3 歸一化解法

相對優勢劃線法和期望支付等值法分別在求解2×2型博弈的純策略納什均衡和混合策略納什均衡方面有各自優勢，但缺陷是適用范圍有限，容易造成解得遺漏。一個自然的想法是如何將兩種方法歸一化，探求對2×2型博弈的一般性求解方法。

歸一化解法基于最優反應函數法，能有效減輕該方法在使用過程中的計算量。由表3，產品選擇“協調”博弈中局中人1、2的支付矩陣是：經局部變換后的對角陣分別是：于是a1=4、a2=1、b1=1、b2=4，。查閱表2知該2×2型博弈有三個納什均衡：，分別是純策略納什均衡（產品甲，產品甲）、（產品乙，產品乙）和混合納什均衡

通過方法比較后不難發現，2×2型博弈決策均衡的歸一化解法利用納什均衡不變性定理，可將復雜的求解過程“簡單化、程序化和規范化”，具有普適性特征，且很好地解決了其他方法解的遺漏問題。

[1]王文舉.經濟博弈論基礎[M].北京：高等教育出版社,2010.

[2]Nash J.Equilibrium Points in n-person Games[J].Proceedings of the National Academy of Science,1950,(36).

[3]Debreu D A.Social Equilibrium Existence Theorem[J].Proceedings of the National Academy of Science,1952,(38).

[4]李正龍.雙人靜態博弈純戰略納什均衡存在性判別[J].應用數學與計算機學學報,2001,15(1).

[5]朱年磊,李榮生.靜態博弈純戰略均衡存在性判別法[J].曲阜師范大學學報,2006，32(1).