一種確定性測量矩陣與快速恢復算法*

唐川雁，朱 皓

（杭州電子科技大學 通信工程學院，浙江 杭州 310018）

0 引 言

壓縮感知（Compressed Sensing，CS）因采樣率不受奈奎斯特采樣定理的限制且可以基本無失真地恢復出原始信號，成為無線通信、生物傳感等領域的熱門研究方向。

壓縮感知的關鍵是測量矩陣的構造和恢復算法的設計。具體地，測量矩陣與稀疏基之間的相關性盡量要小，在對信號進行觀測實現降維處理時，不破壞信號中的有用信息；恢復算法應采用盡量少的測量值快速準確地恢復信號。Candes等人提出約束等距性質（Restricted isometry property，RIP）[1]來判斷測量矩陣的性能優劣。常用的隨機測量矩陣均滿足此性質，如高斯隨機矩陣、傅里葉隨機矩陣等。但是，它的硬件實現和對應恢復算法的設計較復雜，實用性差。因此，Haupt和Bajwa等人提出了托普利茲矩陣、循環矩陣[2-5]，Bajwa等人提出了結構化隨機矩陣[6]，均為確定性測量矩陣，但這些矩陣相比高斯隨機矩陣重構效果較差。Ronald A DeVore提出利用多項式方法來構造確定性測量矩陣[7]，但其對圖像的壓縮倍數有限。文獻[8]提出二元置換塊對角測量矩陣（Binary Permuted Block Diagonal，BPBD）。高度稀疏結構傳感效率高，與常用的稀疏基如小波基等不相關，組成元素簡單、易于硬件實現且重構效果較理想，但其置換過程繁瑣。

本文提出一種簡單的二元塊對角（Binary Block Diagonal，BBD）確定性測量矩陣，能夠降低測量矩陣的計算復雜度，有效促進硬件實現，節約成本。恢復算法分為貪婪算法和凸松弛算法。貪婪算法應用廣泛，典型的有出現時間較早的匹配追蹤（Matching Pursuit，MP）算法[9]。后續許多算法都是在MP算法基礎上改進而來的，如正交匹配追蹤（Orthogonal Matching Pursuit，OMP）算法[10]、分段式正交匹配追蹤（Stagewise Orthogonal Matching Pursuit，StOMP）算法[11]等。OMP算法逐步向前迭代，在余量更新時引入Schmidt正交化處理，不會出現原子的重復選擇，加快了算法的收斂過程，但因其每次迭代過程中的正交化處理使得運算量加大。StOMP算法在OMP算法基礎上每次迭代選擇多列，加速了恢復過程，但其對已選原子不能進行再次篩選，加大了原子誤選概率。本文提出基于離散余弦變換域（Discrete Cosine Transform，DCT）[12]的快速恢復算法。在DCT域中，利用閾值來控制信號的稀疏水平，可預知所提測量矩陣的有效列位置，不需要在每次迭代中尋找與當前殘差的最匹配原子，從而可以高效恢復原始信號。

1 壓縮感知基本理論

設在RN空間中存在一個長度為N的離散信號X，可看作是一個N×1維的列向量。現假設有一組基函數Ψi(i=1,2,…,N)也是N×1維的，若X可用Ψi的線性組合來表示，令Ψi=[Ψ1,Ψ2…,ΨN]，則X可表示為：

式 中 Ψ 為 稀 疏 基（ 變 換 基），α=[α1,α2…,αN]T稱為稀疏矢量。若矢量α只存在至多K個非零值或重要元素，可認為該信號在變換基上是稀疏的，稀疏度為K。CS通過矩陣Φ∈RM×N對信號X(X∈RN)進行觀測實現降維處理，其中K＜M＜N，得到的矢量y∈RM叫做測量矢量（測量值），表達式為：

式中A=Φ×Ψ∈RM×N為恢復矩陣，Φ為測量矩陣。

從測量值y中重構出原始信號X的過程叫做CS的恢復過程，即求解式（2）。因為A不是一個方陣(M＜N)，所以式（2）是一個NP-hard問題。但是，由于X對于基Ψ有稀疏表現，所以恢復過程可由下列步驟完成：

①求稀疏矢量α～：

②重構信號：

如果存在一個約束等距常數δK,0＜δK＜1，使得恢復矩陣A與稀疏矢量滿足：

則可認為測量矩陣滿足RIP條件。只有當測量矩陣滿足該條件時，重建原始信號才能實現。它的等價條件是測量矩陣Φ與稀疏基Ψ不相關。這個條件相比于RIP條件，在實際中更容易證明。通常，用相關系數μ表示這兩個矩陣之間的相關性：

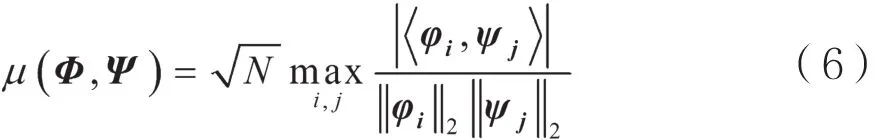
式中φi, i∈{1,2,…,M}代表Φ的行矢量，Ψj,j∈{1,2,…,M}代表Ψ的列矢量。

2 DCT域的閾值處理

稀疏度K的值越小，恢復原始信號所用的測量值越少。因而，應當遵循使得K值盡可能接近0這一原則選擇稀疏基Ψ。常用的稀疏基有小波基、Gabor基和DCT基，也可以通過字典學習訓練法生成稀疏基。此外，為了控制稀疏度K的值，還可以采用閾值法。

DCT已廣泛用于圖像與視頻的壓縮[13]，也可用于壓縮心電圖和肌電圖等生理信號。DCT的變換矩陣為：

式中 i∈ {0,1,…,N-1}和 j∈ {0,1,…,N-1}分別代表矩陣的行和列的數值，而c是一個常數，定義為：

DCT矩陣是正交的，所以它的逆矩陣可通過轉置獲得，即IDCT=DCTT。DCT可將信號的大部分有用信息集中在低頻分量上，而高頻分量上的值通常較小，可以舍棄。因此，可以在DCT域采用類似的閾值法控制稀疏度K的大小，僅保留低于設定閾值的低頻分量，從而降低恢復過程的復雜度。

3 二元塊對角確定性測量矩陣

測量矩陣最初使用的是高斯或貝努利等隨機測量矩陣，它們的元素均獨立服從高斯分布或貝努利分布。這類矩陣滿足RIP性質且能與多數變換基不相關，有較好的重構性能，但計算復雜度高、占用存儲空間大，因此在硬件實現上比較困難。為了降低硬件實現的成本，本文提出了一個簡單的二元塊對角確定性測量矩陣，其構造方式為：

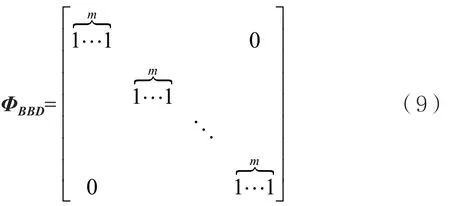
每一行有一個非零塊，每個塊中都包含m=N/M個元素且均為1，每個塊的位置如式（9）所示，其余元素均為0，其中M和N分別表示矩陣的行和列。

矩陣ΦBPBD可以通過對ΦBBD的列進行置換來生成。由于舍棄了置換過程，所以文中提出的測量矩陣ΦBBD在結構上更加簡單，硬件上也更容易實現。

4 基于閾值法的快速重構算法

本文在DCT域中完成閾值法。正如前文所述，DCT將大部分信號信息集中在低頻分量上，剩余的高頻分量在沒有明顯損失的情況下可以舍棄，閾值法即在預先定義的閾值下保持僅有的頻率分量。閾值法在式（3）的過程中完成，能夠促進CS的恢復。本文提出基于DCT閾值法的簡單、快速的恢復算法。

根據提出的確定性測量矩陣ΦBBD，結合恢復矩陣的定義，可以得到：

由式（10）可知，恢復矩陣A與ΨIDCT結構幾乎相同，它的列向量 [?1,?2,…,?N]分別對應于從低頻到高頻的分量。由于提出的ΦBBD是一個確定性矩陣，而ΨIDCT是已知的，因此可事先得知恢復矩陣A中有效列的位置，極大地提升信號的重建效率。

下面給出本文所提恢復算法的實現過程：

輸入：測量向量y，測量矩陣ΦBBD

①初始化：A=ΦBBD×ΨIDCT；

②選擇 A 中前 M 個原子：AM=[?1|?2|…?N]；

③求解線性方程組y=AMα^M；

④得到稀疏矢量 α^=[α^M|0…0]；

⑤輸出信號稀疏估計 X^=ΨIDCTα^。

步驟②直接將恢復矩陣A的前AM個原子取出構成AM，實際等效于在DCT域中進行閾值處理，僅保留用來恢復信號的M個低頻分量。經過這一處理，便可用于信號的重建，這樣在步驟③中僅需求解一個線性方程組，大大簡化了信號的恢復過程。另外，由于不需要在每次迭代中尋找與當前殘差最匹配的原子，故該算法恢復效率較高。

5 仿真結果與分析

對本文所提的BBD確定性測量矩陣進行仿真，從與IDCT矩陣之間的相關性和對信號的重建概率兩方面性能進行實驗。為了比較，對高斯測量矩陣和BPBD測量矩陣也進行了仿真實驗。選擇OMP算法、StOMP算法與本文所提基于閾值法的快速恢復算法進行仿真，比較了三種算法對信號的重建概率和它們的恢復時間。

5.1 對所提BBD測量矩陣的性能分析

將所提測量矩陣ΦBBD、ΦBPBD和ΦGaussian作對比分析，分別計算三種不同測量矩陣與IDCT矩陣間的相關性與不同M值之間的關系，其中相關性用式（6）的相關系數來描述。實驗中，原始信號長度N取500，測量值M以50為步進遍歷50～450，得到三種測量矩陣與IDCT的相關系數隨M的變化曲線，如圖1所示。由圖1可知，高斯測量矩陣與IDCT矩陣的相關系數μ最大，且μ的值隨著M的增大沒有持續減小。而BPBD矩陣和BBD矩陣的相關系數隨著M的增大而減小，當M≥100時，BBD矩陣與BPBD矩陣的相關系數接近。可見，本文提出的BBD測量矩陣與BPBD測量矩陣在相關性方面性能一致，且明顯高于高斯測量矩陣。

圖1 三種矩陣的相關系數比較結果

下面比較三種測量矩陣對信號的重建概率，恢復算法采用OMP算法，原信號長度N取500，分別取M為35、45，用三種測量矩陣對原始信號進行觀測，稀疏度K以1為步進遍歷1～50，重復實驗100次求平均重建概率，得到如圖2所示的重建概率隨稀疏度的變化曲線。

圖2 三種測量矩陣對信號的重建概率

由圖2可知，使用OMP恢復算法時，本文所提的BBD矩陣在K＜M時重建概率高于高斯隨機矩陣、BPBD矩陣，且只有當K接近M時重建概率才開始下降，而高斯隨機矩陣和BPBD矩陣在K遠小于M時就開始下降，說明用所提的BBD矩陣，OMP算法的性能明顯提高。

5.2 對所提基于DCT閾值法的恢復算法性能分析

用所提的BBD測量矩陣對信號進行觀測，分別用基于DCT閾值法的恢復算法和OMP算法、StOMP算法對信號進行恢復，對信號的壓縮程度用壓縮比進行描述，壓縮比定義如下：

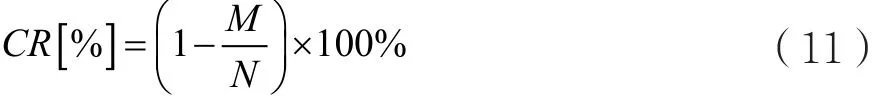
式中M為測量向量的長度，N為原始信號的長度。

用本文所提的BBD測量矩陣分別取M為35和45對原始信號進行觀測，然后分別用三種恢復算法對測量值進行恢復，做出重建概率隨稀疏度的曲線如圖3所示，同樣的重建概率為重復實驗100次的平均重建概率。

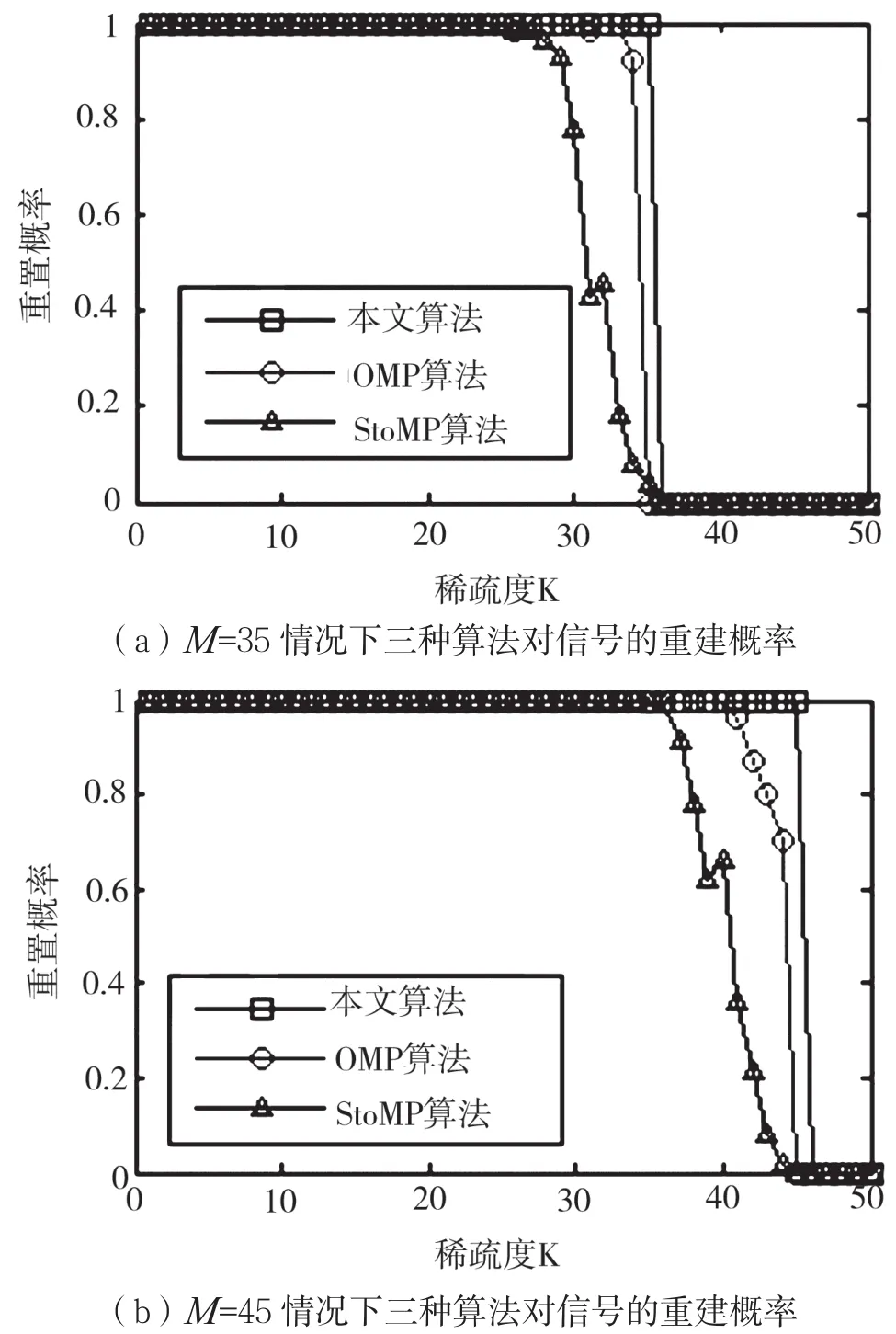
由圖3可知，在M為35時，OMP算法和StOMP算法需要稀疏度分別小于33和26時重建概率為100%，而所提恢復算法在稀疏度小于等于M時重建概率均為100%；M為45時，OMP算法和StOMP算法需要稀疏度分別小于41和35時重建概率為100%，而所提恢復算法在稀疏度小于等于M時重建概率均為100%。這說明在不同測量值M時，本文所提的恢復算法均可以在小于等于M的稀疏度下準確重構原始信號，而OMP算法、StOMP算法需要稀疏度較小時才能準確重構原始信號。所以，在重構概率上，本文所提出的基于DCT閾值法的恢復算法是性能最好的。

下面比較所提快速恢復算法、OMP算法、StOMP三種算法的恢復時間Tr和平均信噪比在不同壓縮比CR下的情況，結果如圖4所示。

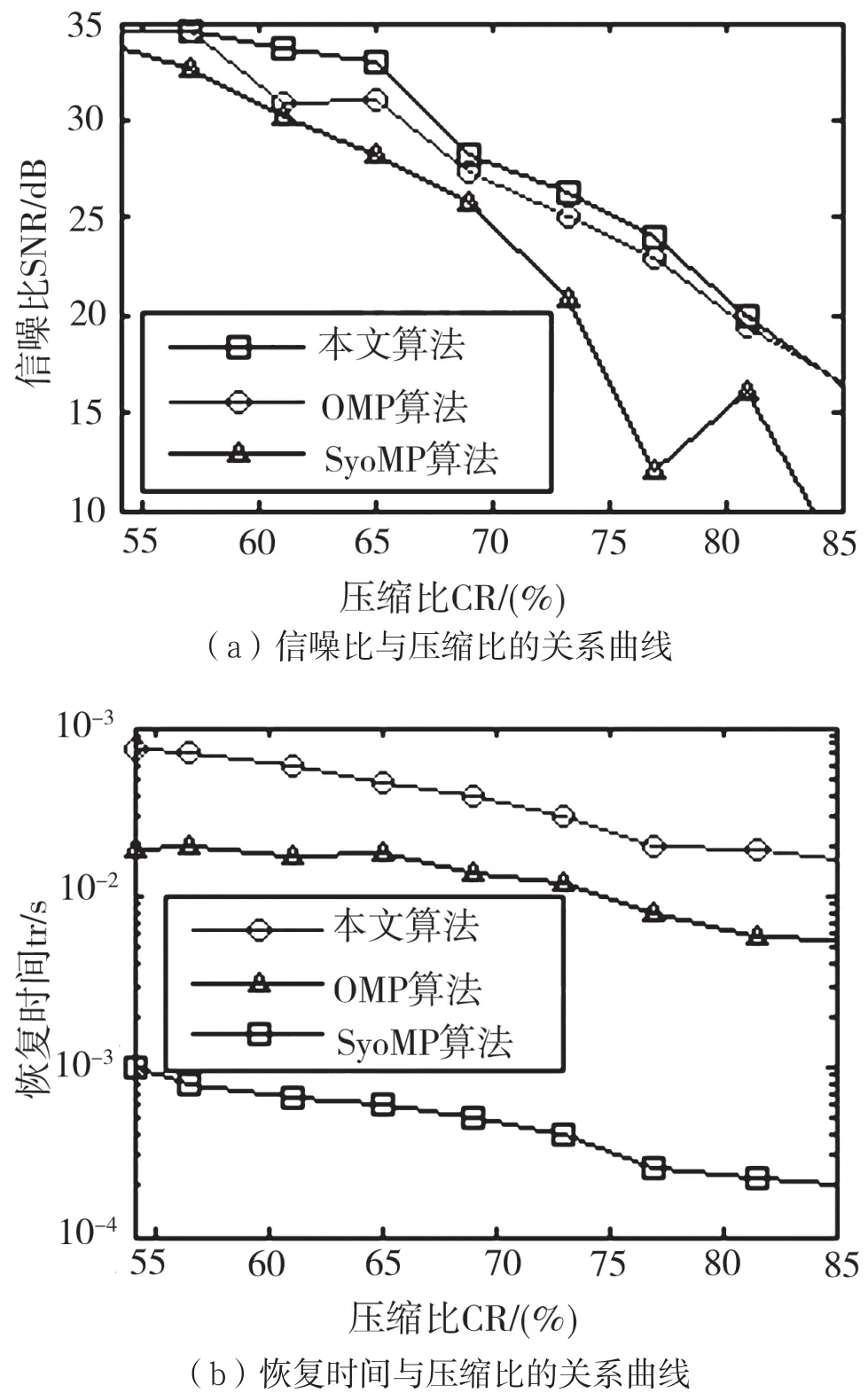
圖4 信噪比和恢復時間與壓縮比的關系曲線

由圖4可知，隨著壓縮比的增大，三種算法的恢復時間都減小，說明測量點數越少，恢復信號所用時間越短。由于OMP算法需要多次迭代選擇與殘差最匹配的原子，所以其恢復時間最長，而StOMP算法在每次迭代過程中選擇了多個原子，所以在相同壓縮比下比OMP算法恢復時間短。而所提基于DCT閾值法的快速重構算法完全舍棄了迭代選擇最佳原子的過程，因此在相同壓縮比下重構效率最高，所用的恢復時間最短，比OMP算法、StOMP算法的速度均快了10倍以上。由平均信噪比與壓縮比CR之間的關系曲線可看出，在相同壓縮比下，所提恢復算法的信噪比比OMP算法、StOMP算法大，說明提出的基于DCT閾值法的快速恢復算法相比于OMP算法、StOMP算法具有更好的性能。

6 結 語

針對傳統隨機測量矩陣的不足，提出了一種簡單的確定性測量矩陣，即二元塊對角確定性測量矩陣，并基于此測量矩陣對信號進行觀測降維，提出了在DCT域完成閾值處理且簡單快速的恢復算法。仿真實驗的結果表明，所提測量矩陣與隨機測量矩陣相比，在重構概率上具有更好的性能，且所提恢復算法在同等壓縮比下的信噪比均高于OMP算法、StOMP算法，所需的恢復時間也比OMP算法、StOMP算法快了10倍以上。

[1] Candès E J.The Restricted Isometry Property and Its Implications for Compressed Sensing[J].Comptes Rendus Mathematique,2008,346(09-10):589-592.

[2] Rauhut H.Circulant and Toeplitz Matrices in Compressed Sensing[m].Mathematics,2009.

[3] Bajwa W U,Haupt J D,Raz G M,et al.Toeplitz-Structured Compressed Sensing Matrices[C].Statistical Signal Processing,2007:294-298.

[4] Yin W.Practical Compressive Sensing with Toeplitz and Circulant Matrices[C].Proceedings of SPIE-The International Society for Optical Engineering,2010:7744.[5] Sebert,Florian Z,Yi M,et al.Toeplitz BlockMatrices in Compressed Sensing and Their Applications in Imaging[C].Information Technology and Applications in Biomedicine,2008:47-50.

[6] Do T T,Tran T D,Gan L.Fast Compressive Sampling with Structurally Random Matrices[C].IEEE International Conference on Acoustics,Speech and Signal Processing IEEE,2008:3369-3372.

[7] Devore R A.Deterministic Constructions of Compressed Sensing Matrices[J].Journal of Complexity,2007,23(04):918-925.

[8] He Z,Ogawa T,Haseyama M.The SimplestMeasurement Matrix for Compressed Sensing of Natural Images[C].IEEE International Conference on Image Processing,2010:4301-4304.

[9] Mallat S G,Zhang Z.Matching Pursuits with Timefrequency Dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415.

[10] Tropp J,Gilbert A C.Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

[11] Donoho D L,Tsaig Y,Drori I,et al.Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2012,58(02):1094-1121.

[12] Khayam S A.The Discrete Cosine Transform(DCT)[M].London:Digital Image Processing. Springer,2008:367-373.

[13] Li Q,Han Y,Dang J.Image Decomposing for Inpainting Using Compressed Sensing in DCT Domain[M].New York:Springer-Verlag Inc.,2014.