GMS在大石橋灌區(qū)信息化的應(yīng)用
李秀麗
(沈陽智信佰達(dá)科技有限公司,遼寧 沈陽 110000)
1 GMS概述
EM平臺全稱Easy-Monitoring平臺,是基于云平臺架構(gòu)的物聯(lián)網(wǎng)監(jiān)測平臺,GMS是EM下的一個應(yīng)用子平臺,是水利行業(yè)中農(nóng)水方向的專業(yè)平臺,涉及灌區(qū)信息化、水價改革、生態(tài)測流、水庫調(diào)度、農(nóng)村飲用水等業(yè)務(wù)領(lǐng)域[1]。GMS總體架構(gòu)共分為四層,分別是立體智能感知、網(wǎng)絡(luò)環(huán)境、數(shù)據(jù)中臺和智慧應(yīng)用,GMS支持應(yīng)用模塊的自由組合,采用工具式研發(fā),自由定義式組合,用戶可根據(jù)不同需求選擇板塊中不同功能模塊的不同子功能,從而組成一套具有自身特色的業(yè)務(wù)應(yīng)用平臺,同時也提供對外接口,滿足千人千面的個性化需求。GMS的應(yīng)用模塊有上百種,用戶都是根據(jù)自己的實際情況來選擇,對于灌區(qū)用戶來說用水調(diào)度和用水計量是需求最多的功能模塊,系統(tǒng)特有的數(shù)據(jù)匯集和用水分析模塊可以更有效地協(xié)助用戶對其灌區(qū)內(nèi)各渠道的水量使用情況進(jìn)行實時監(jiān)測,并給出告警和建議[2]。
2 大石橋灌區(qū)GMS功能
大石橋灌區(qū)的GMS功能主要與灌區(qū)用水調(diào)度、用水計量和水費征收的內(nèi)容相關(guān)。通過系統(tǒng)的一張圖展示功能將灌區(qū)各類統(tǒng)計分析數(shù)據(jù)以交互式圖形或圖表的形式進(jìn)行統(tǒng)一的展示,直觀形象地分析灌區(qū)關(guān)鍵部位數(shù)據(jù)采集監(jiān)測情況、引供水量情況、水費征收情況等,為灌區(qū)的管理決策提供快速的數(shù)據(jù)支持。業(yè)務(wù)應(yīng)用部分根據(jù)國家要求和相關(guān)標(biāo)準(zhǔn)設(shè)計了水量統(tǒng)計查詢、實時數(shù)據(jù)展示、水費征收臺賬、設(shè)備運行狀態(tài)、值班管理、通訊錄管理運行管理等實用的功能模塊,用信息化手段協(xié)助灌區(qū)用水管理和調(diào)度,解決“最后一公里”問題[3]。
以上功能是現(xiàn)在各灌區(qū)應(yīng)用平臺軟件的基礎(chǔ)功能,GMS主要功能特點是智能分析和數(shù)據(jù)整編能力。利用數(shù)據(jù)中臺可以將數(shù)據(jù)進(jìn)行精細(xì)化處理,處理后的數(shù)據(jù)可以根據(jù)不同模塊的需求進(jìn)行整編,整編數(shù)據(jù)可以與各節(jié)點關(guān)聯(lián),除了判斷單個節(jié)點的問題外還可以進(jìn)行關(guān)聯(lián)分析和判斷,從而達(dá)到智能分析的效果。簡單來說智能分析就是以糾錯、整編后的數(shù)據(jù)為基礎(chǔ),不僅分析單個監(jiān)測站點,還能夠以灌區(qū)渠系組成和上下級關(guān)聯(lián)的方式來整體考察數(shù)據(jù)的合理性,從而達(dá)到輔助調(diào)度和支持決策的目的。
2.1 數(shù)據(jù)匯集
智能分析是通過數(shù)據(jù)中臺來實現(xiàn)的,數(shù)據(jù)匯集則是數(shù)據(jù)中臺的第一層,GMS的數(shù)據(jù)匯集是以設(shè)備為單位進(jìn)行管理的,通過不同的設(shè)備類型對接不同的通訊接口和協(xié)議,制定不同的數(shù)據(jù)表格,轉(zhuǎn)存不同的數(shù)據(jù)庫,如果傳輸終端是RTU則增加與終端機(jī)的校時功能,保證補發(fā)數(shù)據(jù)的時間順序不與實時數(shù)據(jù)混淆。對于特殊的設(shè)備還能進(jìn)行公式的管理和寫入,例如雷達(dá)水位計的空高如何轉(zhuǎn)換成水位或水深的公式,振弦式水位設(shè)備的頻率如何轉(zhuǎn)換成壓力的公式,再由壓力如何轉(zhuǎn)換成水位或水深的公式等。這樣的數(shù)據(jù)接收與處理不僅節(jié)省了后續(xù)平臺運算的壓力,也為數(shù)據(jù)整編分析夯實了基礎(chǔ)。
2.2 數(shù)據(jù)交互與分析
數(shù)據(jù)交互與分析是數(shù)據(jù)中臺的第二層,在數(shù)據(jù)匯集入庫后,平臺會根據(jù)設(shè)備編號與應(yīng)用端的節(jié)點進(jìn)行匹配,內(nèi)容包括設(shè)備地點、坐標(biāo)、用途、上下級關(guān)系、告警閾值、合理性范圍等。其中上下級關(guān)系、告警閾值和合理性范圍是在業(yè)務(wù)應(yīng)用平臺設(shè)置的,三者的分析邏輯也是應(yīng)用平臺通過結(jié)合實際情況給出的,在不同的應(yīng)用場景下定制開發(fā)了通用的基礎(chǔ)分析模塊,然后再由組合的方式針對某一情況選取,最終得到類似定制開發(fā)的應(yīng)用[4]。
2.3 灌區(qū)業(yè)務(wù)應(yīng)用
灌區(qū)業(yè)務(wù)應(yīng)用按照每個灌區(qū)的實際情況,規(guī)劃出渠系關(guān)系并且按照節(jié)點的方式傳遞給數(shù)據(jù)層,讓業(yè)務(wù)邏輯與監(jiān)測站點能夠匹配成功,然后在模型方法庫中設(shè)置相關(guān)的計算和分析模型,針對灌區(qū)計量和用水調(diào)度設(shè)置告警,分析用水情況,系統(tǒng)分析不是單純的數(shù)值設(shè)定或者公式計算,而是通過多個站點的關(guān)聯(lián),上下級匹配和多參數(shù)設(shè)置最終達(dá)到智能分析的目的,能夠在復(fù)雜的用水環(huán)境下給出科學(xué)的告警,輔助管理員查找原因,提高灌區(qū)運行效率和效益[5]。
3 GMS應(yīng)用實例
營口灌區(qū)(大石橋市)位于遼寧中部平原的南端,地處大遼河最下游左岸,本地區(qū)屬季風(fēng)氣候,多年平均降水量為652 mm。灌區(qū)屬于平原地區(qū),地勢東北高,西南低,灌區(qū)內(nèi)地勢平坦,多河網(wǎng)和洼地,主要利用渾河、太子河上游水庫下泄到大遼河水量進(jìn)行灌溉。總土地面積912.92 km2,水田灌區(qū)灌溉面積51 萬畝,是遼寧省大型灌區(qū)之一。
大石橋市水田灌區(qū)灌溉面積分布在水源、溝沿、石佛、旗口、高坎、虎莊六個鎮(zhèn),共有113 個行政村、22.9 萬人,近幾年平均糧食產(chǎn)量8 億kg。灌區(qū)有泵站160 座,總裝機(jī)容量40576 kW。灌區(qū)有干渠256.02 km,支渠568.8 km、斗渠1530 km,農(nóng)渠4080 km。灌區(qū)排水總干溝347.16 km,排水干、支溝渠776.44 km。
三八站是大石橋灌區(qū)的一個外河提水泵站,干渠灌溉面積21041 畝,水泵7 臺,其中900 mm管徑4 臺功率180 kW,700 mm管徑3 臺功率155 kW。根據(jù)用戶需求對三八站所有水泵安裝流量計統(tǒng)計用水總量,在七支渠、八支渠、十三支渠安裝流速流量系統(tǒng)用于監(jiān)測渠道用水量,十三支渠的下屬所有斗渠:十三支北、十三支西和十三支南也都安裝計量設(shè)備,通過這種安裝配置方法,能夠得到一個典型渠系的水量關(guān)系和渠道灌水效率。
整個監(jiān)測系統(tǒng)設(shè)備分為兩類:一類是管道流量計;另一類是明渠流速流量計。管道流量計共計7 套都安裝在三八站內(nèi)監(jiān)測7 臺水泵的流速、流量以及臺時,明渠流速流量計安裝于各支渠和斗渠的渠首位置用于監(jiān)測渠道用水量。各渠道均為全部襯砌的梯形渠道。根據(jù)以上現(xiàn)場條件應(yīng)用平臺使用兩種數(shù)據(jù)儲存格式進(jìn)行匯集,同時對應(yīng)的參數(shù)設(shè)置。
管道流量計是7 套設(shè)備為一個節(jié)點(一個泵站),各渠道渠首為一個節(jié)點,節(jié)點間有等級劃分,數(shù)據(jù)匯集層會按照業(yè)務(wù)應(yīng)用層的設(shè)置來匹配節(jié)點,即三八站為一級節(jié)點,七、八、十三支渠為二級節(jié)點,十三支北、西、南斗渠為三級節(jié)點,由于渠道全部襯砌所以水利用系數(shù)干渠為0.85 ~0.91,支渠為0.89 ~0.93,畝均用水量由三八站抽水總額確定,各渠道結(jié)合水利用系數(shù)與標(biāo)注值進(jìn)行對比,誤差范圍設(shè)置在10%以內(nèi)[6]。以2019 年7 月份用水量統(tǒng)計數(shù)據(jù)為例,GMS在實時監(jiān)測數(shù)據(jù)中實時統(tǒng)計泵站7 月總用水量為4884908 m3,畝均用水量232.16 m3/畝,各渠道用水量結(jié)果見表1。
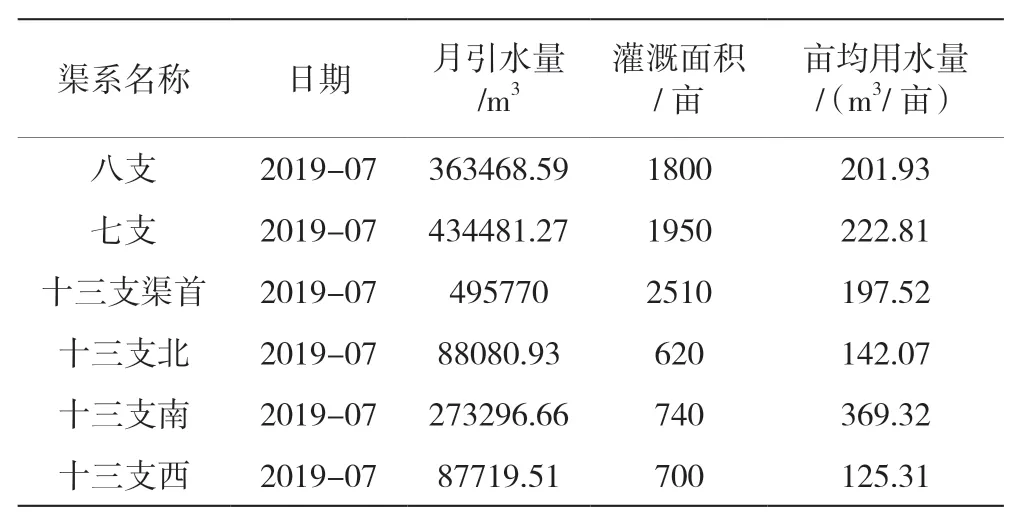
表1 7月份各渠道用水量表
從畝均用水量進(jìn)行考量,由于七、八支渠在上游離渠首較近,十三支距離七八支還有3 km的距離,其下屬斗渠距離十三支渠首還有3.6 km的距離,所以雖然全程都是混凝土襯砌渠道但是水量損失也很大,但總體來看計量設(shè)備的誤差在10%以內(nèi)。在7 月運行期間系統(tǒng)對十三支南、十三支渠北和十三支渠西斗渠提出了告警,原因是畝均用水量不合理:南斗渠超出了正常值范圍,其他兩個斗渠則低于正常值范圍。收到告警后對數(shù)據(jù)進(jìn)行分析:將十三支各斗渠的用水量之和與支渠渠首輸水量對比可知總水量合理,即三個斗渠水量和小于十三支渠首的引水量,并且渠道水利用系數(shù)為0.9 符合襯砌渠道用水系數(shù)。那么這個結(jié)果說明,十三支南斗渠存在過度用水的情況并非計量設(shè)備的數(shù)據(jù)錯誤,同時也解釋了為何系統(tǒng)沒有對十三支渠渠首提出告警,其他兩斗渠告警是因為十三支渠水量增加,使得其他兩斗渠水量從數(shù)據(jù)上看低于誤差10%造成的。用戶根據(jù)此結(jié)果去現(xiàn)場勘結(jié)果發(fā)現(xiàn)在十三支南斗渠附近有若干養(yǎng)魚的方塘,多余的水量都是方塘使用的,據(jù)此可以對方塘采取用水收費以及在旱情發(fā)生時禁止方塘用水等措施,保證灌區(qū)用水優(yōu)先[7]。
4 結(jié)論
通過以上實例可以看出系統(tǒng)的智能判斷在合理選擇計算模型的情況下可以給出合理的輔助告警和分析結(jié)果,并且支持多種設(shè)備和條件的組合,根據(jù)渠系組成折算水量損失,這對于渠系眾多,但是關(guān)系明確的灌區(qū)十分適用,同時系統(tǒng)還支持水泵、閘門和渠道的臺時、瞬時流速流量、日、月、年引水量的表格統(tǒng)計[8]。通過GMS的輔助,用戶對已經(jīng)安裝計量設(shè)備的渠道供水情況有了準(zhǔn)確的了解,也為水費的征收提供了可靠的依據(jù),同時還能發(fā)現(xiàn)渠道用水效率和用水過量的問題,經(jīng)過一段時間的校核和調(diào)研,大石橋灌區(qū)的用水調(diào)度工作更加合理和規(guī)范,由于發(fā)現(xiàn)了魚塘取水的情況,對有此情況的渠道進(jìn)行重新計量和收費,減輕了種糧農(nóng)民的負(fù)擔(dān),也為今后的用水調(diào)度提供數(shù)據(jù)支撐。

