基于層間相似性的時序網絡節點重要性研究?

楊劍楠 劉建國 郭強

1)(上海理工大學復雜系統科學研究中心,上海 200093)

2)(上海財經大學金融科技研究院,上海 200433)

1 引 言

時序網絡考慮節點之間的交互關系和次序,可以更加準確地刻畫手機通訊、社交等復雜系統的交互關系[1?5].節點重要性的評價方法有很多種,如度中心性、介數中心性、緊密度中心性、特征向量中心性、K-核中心性等,不同的評價方法其側重點也各有不同[6?8].劉建國等[6]分別從網絡結構和傳播動力學的角度,對現有的復雜網絡中節點重要性排序方法進行了系統的比較、歸納與總結.Liu等[9]綜合網絡結構和傳播動力學特征進行耦合分析,利用差分方程考察傳播過程,對節點重要性進行排序.盡管對于節點重要性排序的研究在靜態網絡上已經取得了一定進展,但時序網絡不同于靜態拓撲結構的網絡,由于時間維度的引入,網絡的連邊隨時間會間斷性地出現和消失[5,10].所以,近些年人們開始對時序網絡節點重要性的研究方法進行探究.Tang等[11,12]基于時間切片的網絡,通過時序最短路徑定義了時序介數中心性和時序緊密度中心性等統計特性,并提出了節點重要性預測及網絡切片方法等.鄧冬梅等[13,14]基于節點邊貢獻值來評價節點重要性,考慮網絡時間屬性并定義事件相關節點感染方式,提出了時序社交網絡中節點重要性評價指標與排序算法.Kim和Anderson[15]在構建時序網絡時規定每個時間切片上的事件僅有一次,并將切片間用有向邊連接,轉化為沿時間單向的有向靜態圖,從而定義了有向時序圖的度中心性、介數中心性和緊密度中心性.Huang和Yu[16]將文獻[9]中考慮動力學指標的重要節點識別方法引入時序網絡中,對節點重要性進行度量.

但上述方法都只考慮時間切片上的連接關系,為了完整地表示時序網絡的結構演變及其動力學過程,還需要考慮不同時間切片之間的連接關系.Taylor等[17]考慮用多層耦合網絡分析的方法,將時序網絡按層間關系和層內關系建立超鄰接矩陣(supra-adjacency matrix,SAM),并定義了基于特征向量的中心性指標和節點重要性隨時間波動的評判指標.然而,經典的SAM方法中時序網絡的構建,其層間關系為參數表示,忽略了不同節點層間連接關系的差異性.基于此,考慮到不同節點的層間連接關系應不同,本文將節點的層間連接關系用鄰居拓撲重疊系數表示,提出了基于節點層間相似性的超鄰接矩陣(similarity-based supra-adjacency matrix,SSAM)時序網絡構建方法,利用特征向量中心性指標,獲取節點在各個時間層上的重要性排序,并得到節點重要性隨時間變化的軌跡.通過節點刪除法判斷節點在網絡中的影響力,利用刪除節點后網絡效率的變化情況來評價節點的重要性排序,并與SAM方法的不同參數結果做比較.Workspace和Enrons數據集上的實驗結果顯示,相比于SAM方法,SSAM方法最終的Kendall’sτ值在各時間層上的平均提高,最高為17.72%和12.44%,說明SSAM方法由于避免了節點共用參數可能造成的高估或者低估節點的層間連接關系,所以可以更為恰當地描述時序網絡,從而更準確地識別時序網絡中的重要節點.

2 理論基礎

2.1 時序網絡描述

時序網絡是一個包含了個體及個體間按時間順序相互作用的系統,將個體視為節點,個體間的相互作用視為節點間的連邊,節點間連邊隨時間變化且具有時間先后順序.通常定義一個網絡G=(V,E),其中所有節點構成節點集為V={v1,v2,···,vN},如果不考慮時序網絡中交互事件發生的時長,則時序網絡整個觀察期[0,m]內的邊可以用三元組et=(i,j,t)來描述,表示節點i與節點j在t時刻發生了一次交互,故所有這樣的邊構成邊集E={e1,e2,···,et}.可以將這樣的時序網絡整個觀察期[0,m]按一定時間間隔切分為T個時間窗口(其中時間間隔為m/T),則網絡被分為T個離散有序的時間層網絡G1,G2,···,GT.

2.2 鄰居拓撲重疊系數

鄰居拓撲重疊系數源自文獻[12]提出的時序相關系數,時序相關系數具體表示為

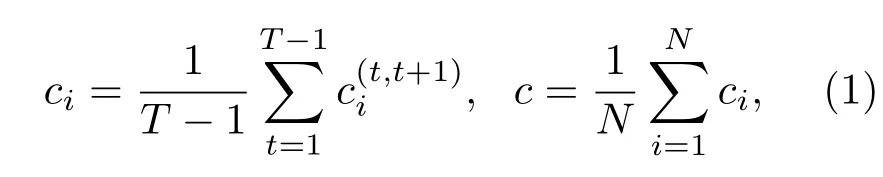
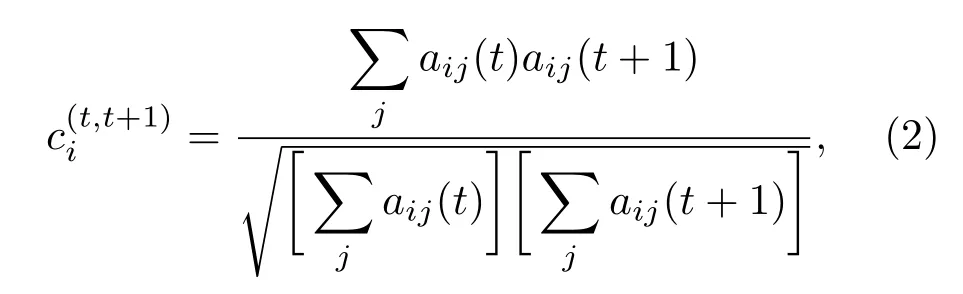
其中aij(t),aij(t+1)分別為相鄰時間層網絡Gt,Gt+1對應的鄰接矩陣中的元素,如果在網絡Gt中節點i與節點j之間有連邊,那么aij(t)=1;否則aij(t)=0.且只有節點j既是節點i在時間層Gt上的鄰居節點同時又是在時間層Gt+1上的鄰居節點時,才有aij(t)aij(t+1)=1;其他情況時aij(t)aij(t+1)=0.

鄰居拓撲重疊系數描述了節點持續出現度及節點鄰居關系的層間相似性.該系數越大表示節點持續出現在兩個相繼時間層,且鄰接關系保持穩定;反之,系數越小表示節點未持續出現在兩個相繼時間層或相鄰時間層上鄰接關系較不穩定.

2.3 經典的SAM時序網絡模型

為了更完整地構建時序網絡,文獻[17]將時序網絡通過層內連接關系和層間連接關系來表示,提出了經典的超鄰接矩陣SAM模型,SAM為NT×NT的分塊矩陣.其中層內連接關系用相應時間層網絡的鄰接關系A(1),A(2),···,A(T)表示,均為N×N的矩陣;層間連接關系用一個參數ω來表示,參數大小調節網絡層間連接關系的緊密程度.對于一個給定節點數為N的時序網絡Γ,其切分的有序時間層網絡集合為Γ={Gt}t=1,2,···,T,T為切分的時間層總數,則其SAM具體表示如下:

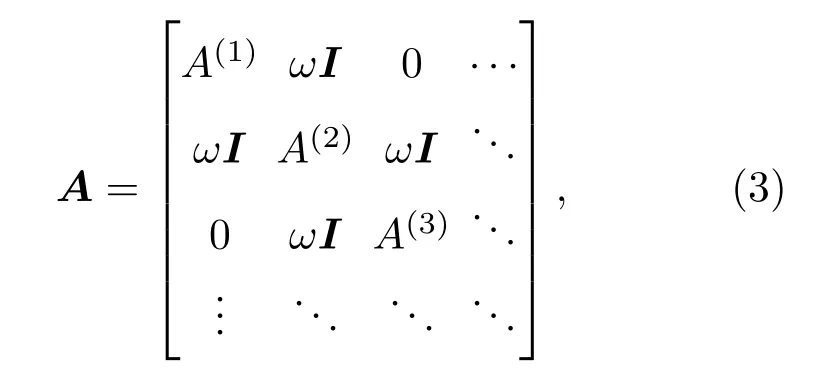
其中,A表示經典的時序網絡模型;A(1),A(2),···,A(T)表示層內連接關系,這里用切分的T個時間層網絡對應的鄰接矩陣表示,依次位于SAM的對角線上,表示有序的時間層網絡:定義aij(t)為鄰接矩陣A(t)中的元素,則aij(t)=0表示在時間層網絡Gt中節點i與節點j間無連邊,aij(t)=1表示有連邊關系;ωI表示層間連接關系,其中ω為可調參數,I為N×N單位矩陣.由于這里僅考慮同一節點在相鄰時間層間的連接關系,所以矩陣其他部分均為0.

3 改進方法

3.1 基于層間相似性SSAM時序網絡模型

由于上述的超鄰接矩陣SAM中,層間關系的參數討論使時序網絡建模復雜化,且節點在相鄰時間層的連接關系用同一參數來表示,忽略了不同節點的差異性.實際上,不同節點對應的層間連接關系應做不同考慮,才能更真實地反映網絡連接的實際情況.基于以上考慮,本文對SAM的層間連接關系做了改進.

考慮到同一節點在相鄰時間層之間的連接關系與其在兩個時間層上的持續出現度及節點的鄰居關系層間相似程度有關,所以我們用鄰居拓撲重疊系數((2)式)來確定層間連接關系,則改進后基于層間相似性SSAM時序網絡模型具體表示形式如下:

其中,A′表示基于節點層間相似性的超鄰接矩陣SSAM;A(1),A(2),···,A(T)同樣表示層內連接關系,這里用切分的T個切片網絡對應的鄰接矩陣表示;C(1,2),C(2,3),···,C(t?1,t)分別表示相鄰時間層之間的連接關系,如C(1,2)表示時間層網絡G1與時間層網絡G2之間的連接關系.C(t?1,t)為N×N的對角矩陣,即C(t?1,t)=即為(2)式節點的鄰居拓撲重疊系數,用來描述節點i的層間相似性,即節點i在時間層網絡Gt?1上與時間層網絡Gt上的共同鄰居數所占的比例.本文也只考慮同一節點在相鄰時間層之間的連接關系,所以SSAM矩陣的其他部分均為0.

圖1給出了一個包含4個節點和3個時間層的時序網絡及SSAM方法的具體表示,其中黑色實線表示層內連接關系,黑色虛線表示層間連接關系.

圖1 基于層間相似性方法的時序網絡建模實例Fig.1.An example of SSAM model for temporal network.

則圖1對應的基于層間相似性的矩陣表示如(5)式.具體地,層內連接關系由各個時間層網絡的鄰接矩陣確定,即(5)式的對角線矩陣塊部分;相鄰時間層的層間連接關系則由各個節點的層間相似性,即(2)式鄰居拓撲重疊系數計算得到;最后,非相繼時間層的矩陣塊部分不做考慮,其元素均為0.

3.2 特征向量中心性

特征向量中心性是評估網絡節點重要性的一個重要指標[6],其不僅考慮節點的重要性程度,同時綜合考慮鄰居節點的重要性程度.所以本文利用特征向量中心性,對時序網絡的節點重要性進行度量,即對上文構建的超鄰接矩陣A′求主特征向量(最大特征值對應的特征向量)ν={υ1,υ2,···,υNT}T.這樣,向量ν的第N(t?1)+i個項即表示第t個時間層上的節點i的特征向量中心性,記為N×T的矩陣W={wit}N×T,則

其中,wit為矩陣W的第i行第t列元素,即為第t個時間層上節點i的特征向量中心性.該指標可以獲得各時間層上節點重要性的排序,同時能夠得到節點在各個時間層網絡重要性隨時間變化的軌跡.

表1為圖1中實例網絡的特征向量中心性指標的結果,并給出了SAM方法參數ω取0.5的特征向量中心性結果做對比.由表1結果可以得到各時間層節點的重要性排序及各個節點重要性隨時間層的變化軌跡,比如對于SSAM方法,第一時間層的G1中節點重要性排序為1-3-4-2,且可以看出1號節點重要性排序隨時間層變化軌跡為1-1-3.

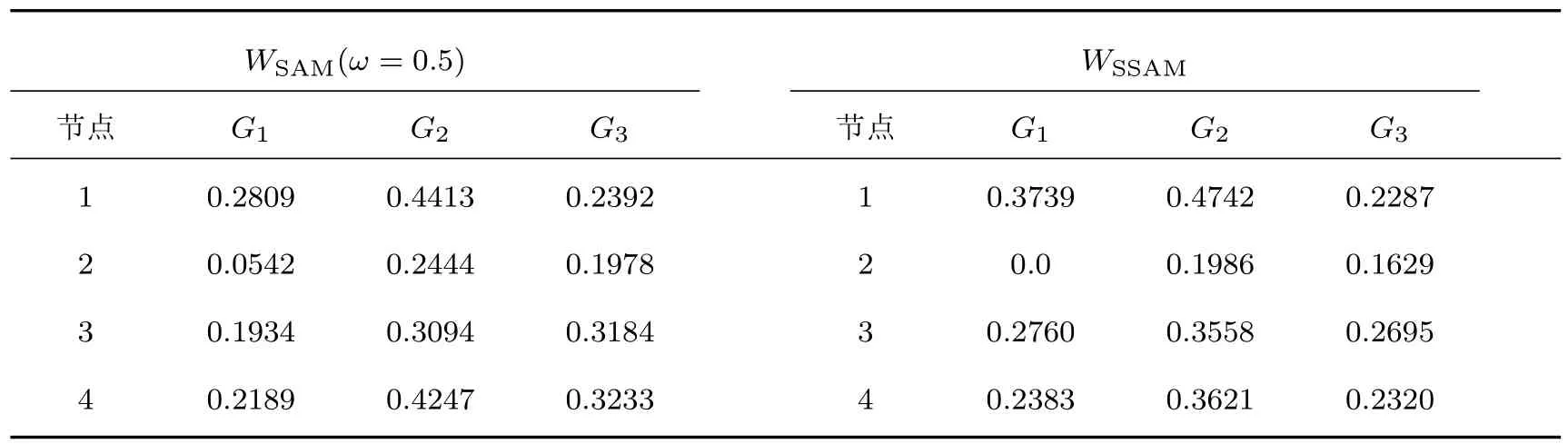
表1 實例網絡中節點的特征向量中心性Table 1.Eigenvector centrality of nodes in temporal network of Fig.1.

結合圖1的時序網絡可以看到,用共同的參數0.5來表示不同節點的層間連接關系,弱化了持續出現且節點層間鄰居相似度高的節點的重要程度,而強化了孤立節點的重要程度.例如第一時間層網絡G1中的1號節點,持續出現在相繼時間層且層內的鄰接關系穩定,雖然其在兩方法中均為該時間層網絡中最重要的節點,但是在SAM方法里1號節點的重要性值較小為0.2809,而SSAM方法里1號節點的重要性值較大為0.3739,說明SAM方法弱化了1號節點的重要性值;對于2號節點,其在G1中為孤立節點,其重要性值應接近于0,而SAM方法高估了G1中2號節點的重要性值.所以不難推出,SAM方法中,當參數較大時,更加強化了孤立節點和層間鄰居相似度低的節點的重要性;而參數較小時,則更加弱化了持續出現且層間鄰居相似度高的節點的重要性.

4 數據實驗與結果分析

4.1 數據描述

為了檢驗SSAM方法對時序網絡節點重要性排序的效果,本文用了兩個實證網絡來進行實驗,分別為Workspace數據和Enrons數據.Workspace[19]為法國某公司通過移動射頻設備獲取的公司員工之間面對面交互產生的交互數據,時間從2013年6月24日到2013年7月3日,數據按天切分;Enrons[20]為美國某公司員工的郵件往來數據,數據從1999年到2002年,為縮減數據,取其中2001年的數據子集,并按月切分.網絡基本統計特性具體描述如表2,其中N表示節點總數,T表示切分的時間層網絡數,C表示節點之間的總交互次數,E表示整個聚合網絡的連邊數,During為該數據記錄的時段.

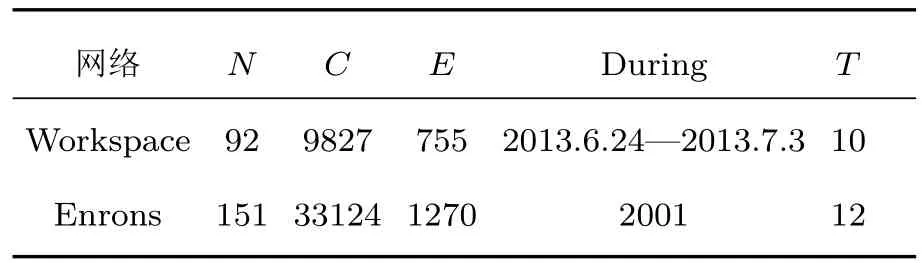
表2 實證網絡基本統計特性Table 2.Basic statistical features of Workspace and Enrons networks.

4.2 評價方法

通常認為,節點重要性不僅體現在節點在網絡中對信息的傳播能力[21?23],也可體現在節點被移除以后對網絡連通的破壞性[8].為進一步檢驗SSAM方法對節點重要性的排序效果,并與SAM方法做對比,文中通過刪除節點后網絡連通性的變化程度來評價節點重要性排序結果.通常認為,刪除節點后,網絡連通性變化越大,則被刪除的節點在網絡中越重要;反之,則節點重要性相對較低.

時序網絡效率是評判時序網絡連通性的一個重要方法,其時序全局效率[17]的具體形式如下:

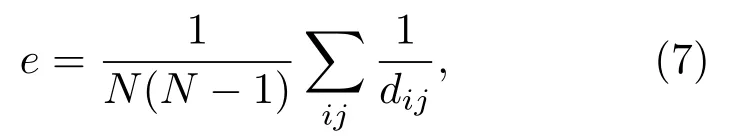
其中,dij為時序網絡中各節點之間的時序距離[12].時序距離通過時序最短路徑計算,時序最短路徑不同于靜態網絡的最短路徑,時序路徑的有效連接都是臨時的,會在某個特定的時間點建立或者斷開,所以時序網絡中的時序最短路徑需要遵從于不同連邊的時間先后順序[4].信息從節點i經過節點k最終傳到節點j,需要在時間維度上要求節點i到k之間的有效連接發生在節點k到j之前,否則信息不能從節點i傳到j.

具體地,圖1所示的時序網絡,假設有信息從t=1時的1號節點開始傳遞,并傳遞到最終t=3時刻結束,且每個時間層上只傳遞一步,則表3給出了最終時序最短路徑的時序距離dij的結果.

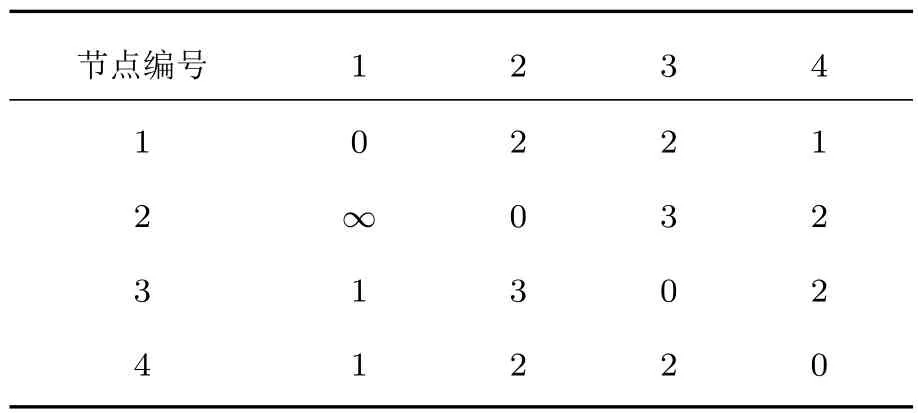
表3 圖1時序網絡中各節點之間的時序距離Table 3.Temporal distance of nodes in temporal network of Fig.1.

最后,用刪除節點前后時序全局效率的差值作為節點重要性的驗證方法.為了與特征向量中心性矩陣W對應,依次刪除各個時間層的節點后重新計算網絡的時序全局效率,得到一個N×T的矩陣E={eit}N×T,再與原時序全局效率e做差值,最終得到刪除節點的時序全局效率差值矩陣E′,其元素

4.3 結果分析

本文基于上述兩個實證網絡數據,依據SSAM方法和SAM方法的不同參數取值計算時序網絡中的各時間層網絡上節點的特征向量中心性,分別得到了SSAM和SAM方法對實證網絡數據的節點重要性排序(其中SAM方法的參數ω取[0.1,0.2,···,1.0]).另外,為了更直觀地檢驗SSAM方法的效果,用節點刪除法得到節點時序全局效率差值排序后,利用Kendall’sτ(肯德爾系數)來評估排序相關性.具體而言,我們對特征向量中心性矩陣W和時序全局效率差值矩陣E′對應的列分別計算Kendall’s tau,即得到相應時刻上節點重要性排序同該時刻刪除節點后網絡效率差值排序的一致性程度.

Kendall’sτ[24]被用來測量兩序列之間排序的相關性程度,其取值范圍為[?1,1],該值越大,則兩序列相關性越強,即說明節點重要性的排序方法更加精確.其中對于兩列數X={x1,x2,···,xn}和Y={y1,y2,···,yn}的Kendall’sτ-b[25]定義為

這里X表示特征向量中心性矩陣W中第t列的排序列表;Y表示通過刪除節點法得到的網絡全局效率差值矩陣E′中對應第t列的排序列表(t=1,2,···,T);sgn(z)為一個分段函數,當z＞0時,sgn(z)=+1,當z＜0時,sgn(z)=?1,當z=0時,sgn(z)=0,這里n為序列長度,即節點總數;其中,ti為X序列中第i個使得sgn(z)=0的xi值的個數,uj為Y序列中第j個使得sgn(z)=0的yj值的個數.

對Workspace數據和Enrons數據分別用SSAM方法和SAM方法的特征向量中心性矩陣與刪除節點法的網絡效率差值矩陣得到相應時間層的Kendall’sτ值如圖2所示:圖2(a)為Workspace數據的結果,圖2(b)為Enrons數據的結果;圖2中橫坐標表示時序網絡切分的各個時間層,縱坐標表示相應時間層對應的Kendall’s tau值;其中黑色小正方形為SSAM方法,其他為SAM方法取不同參數的結果.

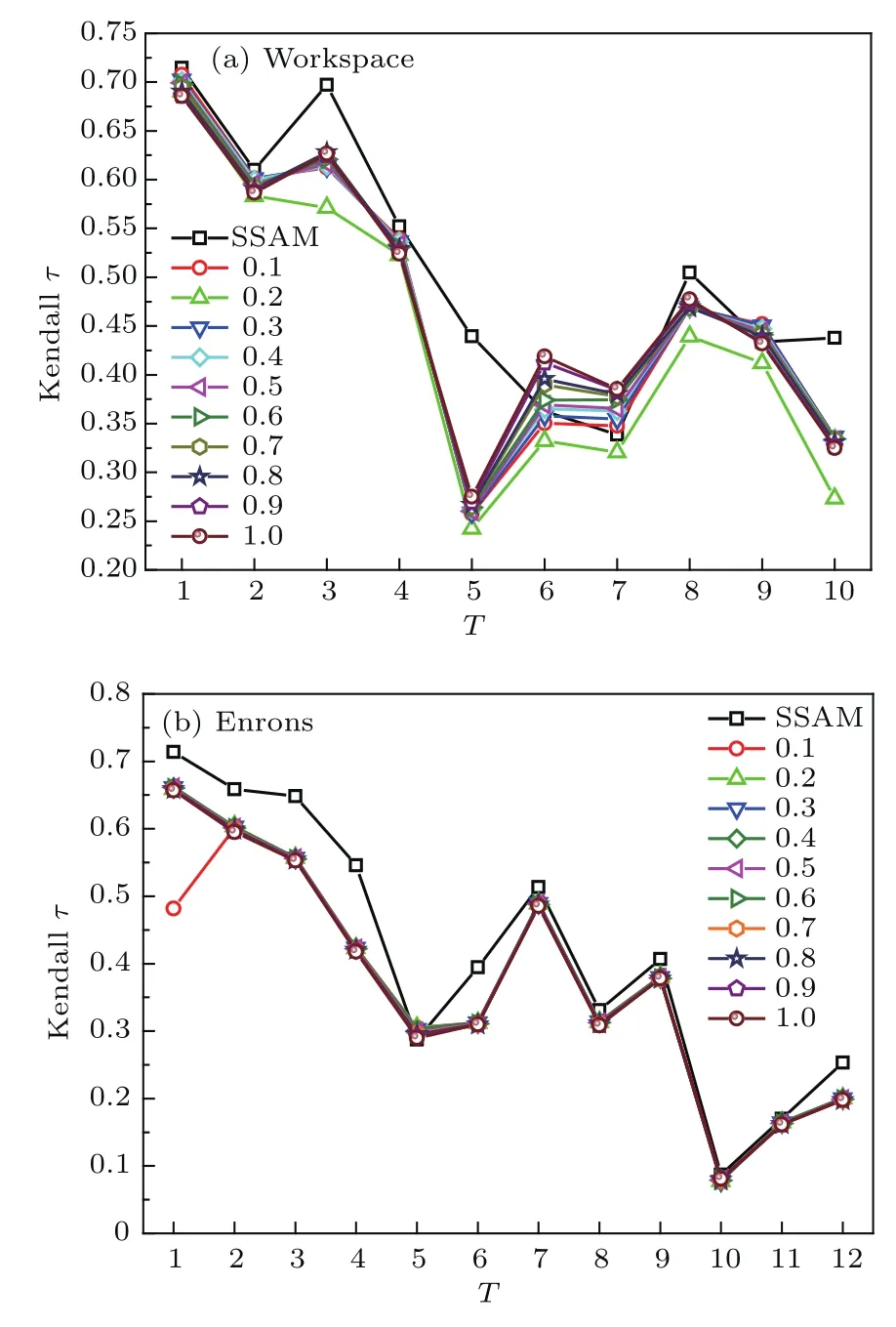
圖2 特征向量中心性與時序網絡效率差值的Kendall’s tau結果 (a)Workspace數據基于層間相似性的超鄰接矩陣方法和經典超鄰接矩陣方法不同參數的Kendall’s τ結果;(b)Enrons數據相應的結果Fig.2.Results of Kendall’s τ for eigenvector centrality and difference of temporal global efficiency:(a)result for Workspace by SSAM method and SAM method;(b)result for Enrons by SSAM method and SAM method.

由圖2中結果可以看到:1)對兩組數據的時序網絡構建中,SAM方法不同參數下得到的Kendall’sτ結果大多相近,Enrons數據集的結果在這點尤為顯著,也就是不同的參數選擇對于節點的特征向量中心性在各個時間層的排序結果影響并不顯著,所以SAM方法中,層間連接關系以參數來討論使得時序網絡構建復雜化,可以考慮用確切的數值來描述層間連接關系;2)SSAM方法得到的Kendall’sτ系數結果大部分比SAM方法的高,也就是基于層間相似性的SSAM方法考慮了不同節點的差異性,能更準確地對時序網絡進行描述,得到的節點重要性排序也更為準確,且對于Enrons數據的結果尤為顯著,其中兩組實證數據SSAM方法的結果相比SAM方法和Kendall’sτ值在各時間層上的平均提高,最高為17.72%和12.44%;3)對于Workspace數據的個別時間層,如t=6,t=7和t=9上,SSAM方法略低于SAM方法,同時該時間層上SAM方法的不同參數結果差別也略大,我們認為此結果是由于實際數據的影響所造成的.

5 結 論

識別網絡中的重要節點一直是復雜網絡的熱點問題,最近有不少工作開始考慮加入時間屬性來研究節點重要性的度量方法,而對于時序網絡的建模也各有不同.本文將時序網絡用層內鄰接關系和層間連接關系共同來描述,并考慮不同節點的差異性及相繼時間層的時序相關性,用節點的鄰居拓撲重疊系數作為時序網絡的層間連接關系,提出了一種基于節點層間相似度的超鄰接矩陣建模方法(SSAM方法),同時利用特征向量中心性來度量節點的重要性.另外,本文利用節點刪除法,通過計算刪除節點前后網絡時序全局效率的變化情況,來評估SSAM方法對節點重要性排序的效果.

兩組實證數據的結果表明,SSAM方法得到的特征向量中心性排序結果大部分比SAM方法的好,且SSAM 方法兩組實驗的Kendall’sτ值較SAM方法在各時間層上的平均提高,最高為17.72%和12.44%.SSAM方法一方面回避了參數討論,另一方面由于考慮了不同節點在相鄰時間層間連接關系的差異性,用基于節點的層間相似度構建時序網絡,避免了節點共用參數可能造成的高估或者低估節點的層間連接關系.綜上所述,本文提出了一種基于層間相似性的時序網絡構建方法,該方法可以更為恰當地描述時序網絡,從而更準確地識別時序網絡中的重要節點.該工作對于時序網絡建模和對時序網絡節點重要性度量方法的研究具有重要意義.

然而,本文基于層間相似性的SSAM方法是考慮了最直觀的鄰居拓撲重疊系數作為相似性的度量指標,而其他相似性指標對于該方法的應用及效果是我們未來可以做進一步討論和研究的問題.另外,本文只考慮同一個節點在相鄰時間層的關系,而實際中,節點之間的聯系不僅依賴于上一時間層內的信息,還可依賴于之前多個時間片段內的信息,并可影響之后多個時間片段,因此具有非馬爾可夫特性;且本文的方法只適用于小規模的數據,這就需要新的更為準確并能用于大規模數據的方法來描述時序網絡.最后,如何進行時序網絡的切分及時間窗大小的選擇一直是個困難的問題[5],不同的切分情況會導致不同的實驗結果,因此如何結合時序網絡的全局結構和網絡動力學來對時序網絡進行構建,并識別出重要節點是未來需要深入研究的問題.

感謝上海理工大學復雜系統科學研究中心林堅洪、楊凱、胡小軍和郭昕宇的交流與討論.參考文獻

[1]Holme P,Saram?ki J 2013Temporal Networks(Heidelberg:Springer)pp1–2

[2]Holme P,Saram?ki J 2012Phys.Rep.519 97

[3]Holme P 2015Eur.Phys.J.B88 234

[4]Liu J G,Ren Z M,Guo Q 2013Physica A392 4154

[5]Ren Z M,Zeng A,Chen D B,Liao H,Liu J G 2014EPL106 48005

[6]Liu J G,Ren Z M,Guo Q,Wang B H 2013Acta Phys.Sin.62 178901(in Chinese)[劉建國,任卓明,郭強,汪秉宏2013物理學報62 178901]

[7]Lü L Y,Chen D B,Ren X L,Zhang Q M,Zhang Y C,Zhou T 2016Phys.Rep.650 1

[8]Ren Z M,Shao F,Liu J G,Guo Q,Wang B H 2013ActaPhys.Sin.62 128901(in Chinese)[任卓明,邵鳳,劉建國,郭強,汪秉宏2013物理學報62 128901]

[9]Liu J G,Lin J H,Guo Q,Zhou T 2016Sci.Rep.6 21380

[10]Zhang Y Q,Cui J,Zhang S M,Zhang Q,Li X 2016Eur.Phys.J.B89 26

[11]Tang J,Musolesi M,Mascolo C,Latora V 2009Proceedings of the 2nd ACM Workshop on Online Social NetworksBarcelona,Spain,August 17–17,2009 p31

[12]Tang J,Scellato S,Musolesi M,Mascolo C,Latora V 2010Phys.Rev.E81 055101

[13]Deng D M,Zhu J,Chen D B,Gao H 2013Comput.Sci.40 26(in Chinese)[鄧冬梅,朱建,陳端兵,高輝2013計算機科學40 26]

[14]Deng D M 2014M.S.Dissertation(Chengdu:University of Electronic Science and Technology of China)(in Chinese)[鄧冬梅 2014碩士學位論文 (成都:電子科技大學)]

[15]Kim H,Anderson R 2012Phys.Rev.E85 026107

[16]Huang D W,Yu Z G 2017Sci.Rep.7 41454

[17]Taylor D,Myers S A,Clauset A,Porter M A 2017Multiscale Model.Simul.15 537

[18]Zhu Y X,Zhang F L,Qin Z G 2014J.Comput.Appl.34 3184(in Chinese)[朱義鑫,張鳳荔,秦志光 2014計算機應用34 3184]

[19]Génois M,Vestergaard C L,Fournet J,Panisson A 2015Network Sci.3 326

[20]Klimt B,Yang Y 2004Machine Learning:ECML2004 217

[21]Zhang Z K,Liu C,Zhan X X,Lu X,Zhang C X,Zhang Y C 2016Phys.Rep.651 1–34

[22]Liu C,Zhan X X,Zhang Z K,Sun G Q,Hui P M 2015New J.Phys.17 113045

[23]Liu C,Zhang Z K 2014Commun.Nonlinear Sci.Numerical Simulat.19 896

[24]Kendall M G 1938Biometrika30 81

[25]Agresti A 2010Analysis of Ordinal Categorical Data(2nd Ed.)(New York:John Wiley&Sons John Wiley&Sons)pp188–191