小尺寸單軸應變Si PMOS溝道晶面/晶向選擇實驗新發現?

陳航宇 宋建軍 張潔 胡輝勇 張鶴鳴

(西安電子科技大學微電子學院,寬禁帶半導體材料與器件重點實驗室,西安 710071)(2017年9月27日收到;2017年12月19日收到修改稿)

1 引 言

單軸應力作用下,Si能帶結構發生變化,空穴遷移率獲得增強.單軸應變Si應用于小尺寸溝道p型金屬氧化物半導體(PMOS)時,器件性能顯著提升,是延續摩爾定律的重要技術手段[1?10].小尺寸單軸應變Si PMOS溝道反型層遷移率與晶面/晶向密切相關,優化設計器件時應選擇合理的晶面/晶向[11?14].目前,有關單軸應變PMOS溝道反型層遷移率晶面/晶向排序結論已有相關文獻[15]報道(見圖1).

圖1(a)—(c)為弛豫情況下Si PMOS反型層載流子遷移率隨晶面/晶向變化圖,當未施加應力時,Si PMOS反型層的空穴遷移率排序為(110)＞(111)＞(001),最大的空穴遷移率出現在(110)晶面沿[10]晶向的溝道方向. 圖1(d)—(f)為應力作用下的情況,由圖可見,1.5 GPa壓應力作用下,(001)晶面的[110]晶向遷移率增強倍數最大,約為弛豫情況下的3倍;(110)晶面與(111)晶面遷移率增強幅度相接近,約為弛豫情況下的兩倍.即應力作用下(001)晶面的增強幅度最大;然而,因為弛豫情況下(110)晶面的[10]晶向空穴遷移率最大,即基數最大,而(001)晶面的遷移率最小,在(110)晶面[10]晶向遷移率增大兩倍的情況下仍然大于(001)晶面的[110]晶向增強3倍的情況.故該研究還表明,最大空穴遷移率出現在(110)晶面的[10]晶向.

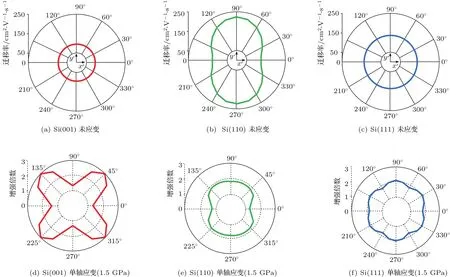
圖1 弛豫Si反型層載流子遷移率與單軸應變反型層載流子遷移率增強圖Fig.1.Inversion layer mobility for unstrained Si and inversion layer mobility enhancement for uniaxial strain.

值得注意的是:一方面,以上文獻[15]報道僅為理論預測排序結果,尚未見涉及全部晶面/晶向排序驗證的實驗結論;另一方面,溝道受力為1.5 GPa應力強度,是以上文獻[15]結論的前提條件,但在實際制作過程中無法引入1.5 GPa的壓應力.這就意味著該理論排序模型還具有局限性.

我們知道,小尺寸應變Si PMOS器件溝道應力是通過其上方源區、漏區及柵覆蓋SiN應力膜而引入的.SiN疏松膜具有膨脹的趨勢,疏松的SiN膜使得PMOS源/漏區域Si材料發生擴張形變,源/漏區域擴張形變進一步引起了溝道區Si材料發生收縮形變.這樣,雖然疏松結構SiN膜未直接接觸PMOS溝道區域,仍然對溝道區施加了壓應變[10,16,17].為了便于理解,該應力引入機理示意圖如圖2.

在器件實際制造過程中,由于SiN膜淀積工藝固定,而Si材料彈性勁度系數又具有各向異性,當PMOS器件溝道選用不同晶面/晶向時,不同晶面/晶向應變PMOS溝道所受應力強度將不同,由于工藝因素間接導致上述文獻[15]溝道反型層遷移率晶面/晶向排序理論模型“失效”.

有鑒于此,本文選用(001),(110),(111)三個典型高對稱晶面Si襯底,利用器件平面工藝,并覆蓋淀積SiN應力膜,制備不同晶面/晶向40 nm溝道小尺寸單軸應變Si PMOS.通過測試所制備的PMOS樣品的轉移特性曲線,獲取小尺寸單軸應變Si PMOS反型層遷移率晶面/晶向排序的實驗結論,并對本文實驗排序結果與文獻[15]理論預測排序結果予以比對說明.

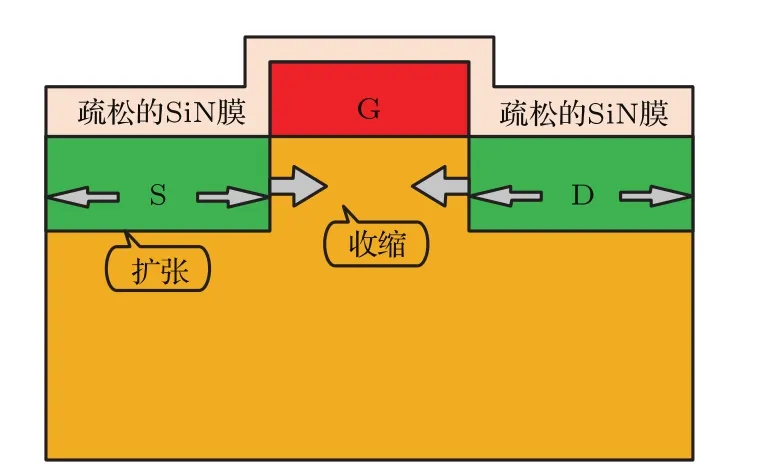
圖2 SiN膜結構與PMOS溝道應力類型對應關系Fig.2.Relationship between SiN film and the type of stress in PMOS channel.

本文有關小尺寸單軸應變Si PMOS溝道反型層遷移率晶面/晶向排序的相關結論,由于考慮了工藝實現因素,與文獻[15]理論預測排序結果相比,可更適于指導實際工藝制備.同時,本文相關分析方法也可為其他應變材料溝道MOS的設計與制備提供重要技術參考.

2 實驗過程

單軸壓應變Si PMOS典型的結構示意圖見圖3,在傳統平面工藝制造好PMOS之后,其溝道壓應力是通過在源漏區上方淀積疏松的SiN薄膜而引入的.

為研究不同晶面/晶向載流子遷移率的大小排序,首先進行實驗方案的確定.本文采用中國科學院微電子研究所40 nm單軸應變Si PMOS工藝,工藝流程如圖4所示.

依據晶體極射赤面投影圖進一步確定溝道晶面/晶向[18],利用圖5所示晶體極射赤面投影圖各晶向之間的角度關系,并參考Si晶圓定位邊晶向,通過旋轉角度,即可確定出不同晶面溝道的各個晶向.

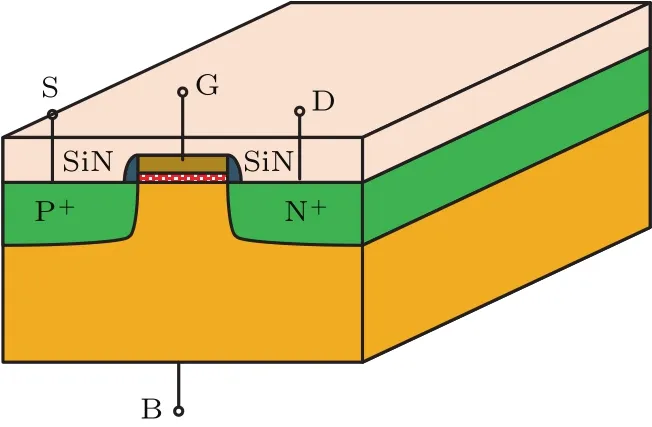
圖3 單軸壓應力Si PMOS結構示意圖Fig.3.Schematic structure of uniaxial strained Si PMOS device.

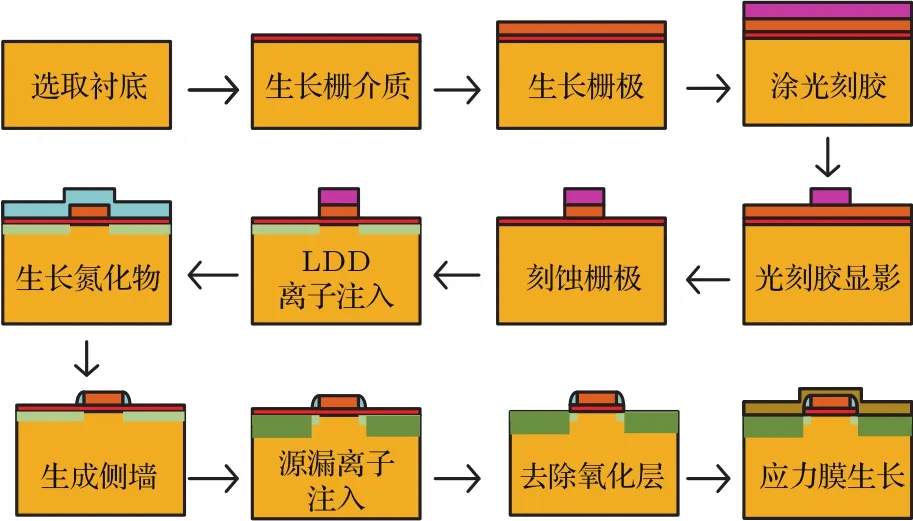
圖4 器件制備工藝流程圖Fig.4.Flow chart of device manufacturing.

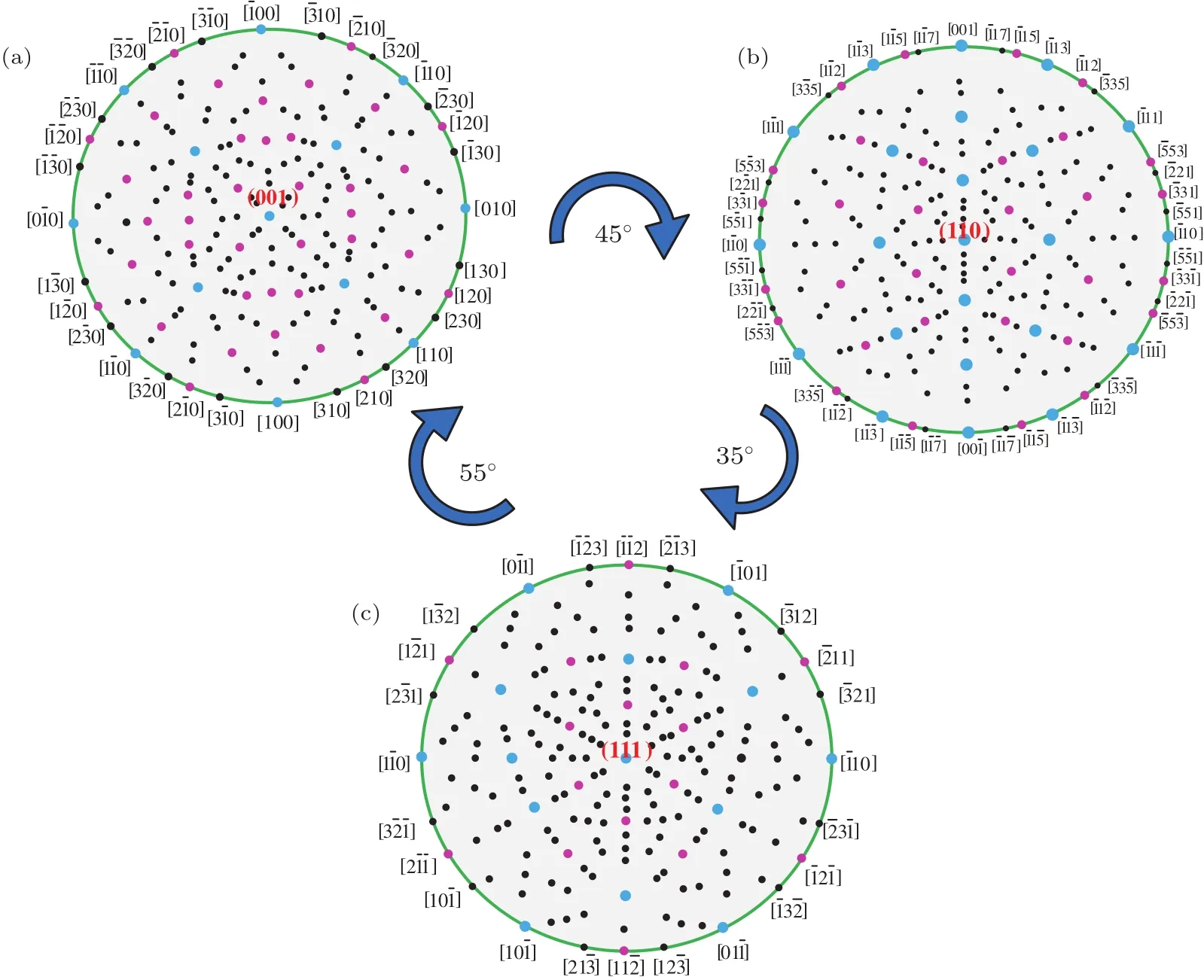
圖5 不同晶面極射赤面投影圖 (a)(001)晶面;(b)(110)晶面;(c)(111)晶面Fig.5.Stereographic projection for different crystal planes:(a)(001);(b)(110);(c)(111).

Si晶體具有對稱性,0°—90°可作為一個周期單元,即可代表所有的晶向.如圖5(a)(001)晶面上0°對應[010]晶向,45°對應[110]晶向,90°對應[100]晶向;圖5(b)(110)晶面上0°對應[001]晶向,90°對應[10]晶向;圖5(c)(111)晶面0°對應[11]晶向,90°對應 [10]晶向.

基于以上討論,本文確定應變PMOS溝道晶面/晶向方案為:在(001),(110),(111)三個不同晶面晶圓上,分別制作弛豫情況與應力作用下溝道角度為0°—90°范圍的晶體管(以15°為一個間隔).其中,(001)晶面相較其他晶面對稱性更高,我們選擇制備了溝道角度為45°—90°范圍的晶體管.圖6為所制備的PMOS的一組顯微照片(以應變(110)晶面為例,其他晶面以及弛豫情況顯微照片與之類似).

利用4200-SCS半導體特性分析系統對上述所制備的不同角度晶體管進行轉移特性曲線測試,獲得實驗數據,并繪制不同晶面/晶向弛豫情況與壓應力作用下的轉移特性曲線.

3 結果與討論

利用飽和區漏電流公式(1),可以間接得出載流子遷移率的大小:

在同一工藝下,不同晶向柵氧化層電容Cox與寬長比W/L相同,忽略應力對于閾值電壓VT的影響,則在同一柵極電壓情況下,電流大小僅與反型層空穴遷移率μ相關.因此通過器件轉移特性曲線,比較不同角度的電流大小即可得出不同角度即不同晶向的遷移率大小.

圖7所示為(001)晶面弛豫情況與壓應力作用下不同角度的PMOS轉移特性曲線.通過對轉移特性曲線的提取分析,獲得柵壓為?1 V時的不同溝道角度的漏極電流大小如圖8,進而可得到(001)晶面不同晶向反型層載流子遷移率的排序如表1.

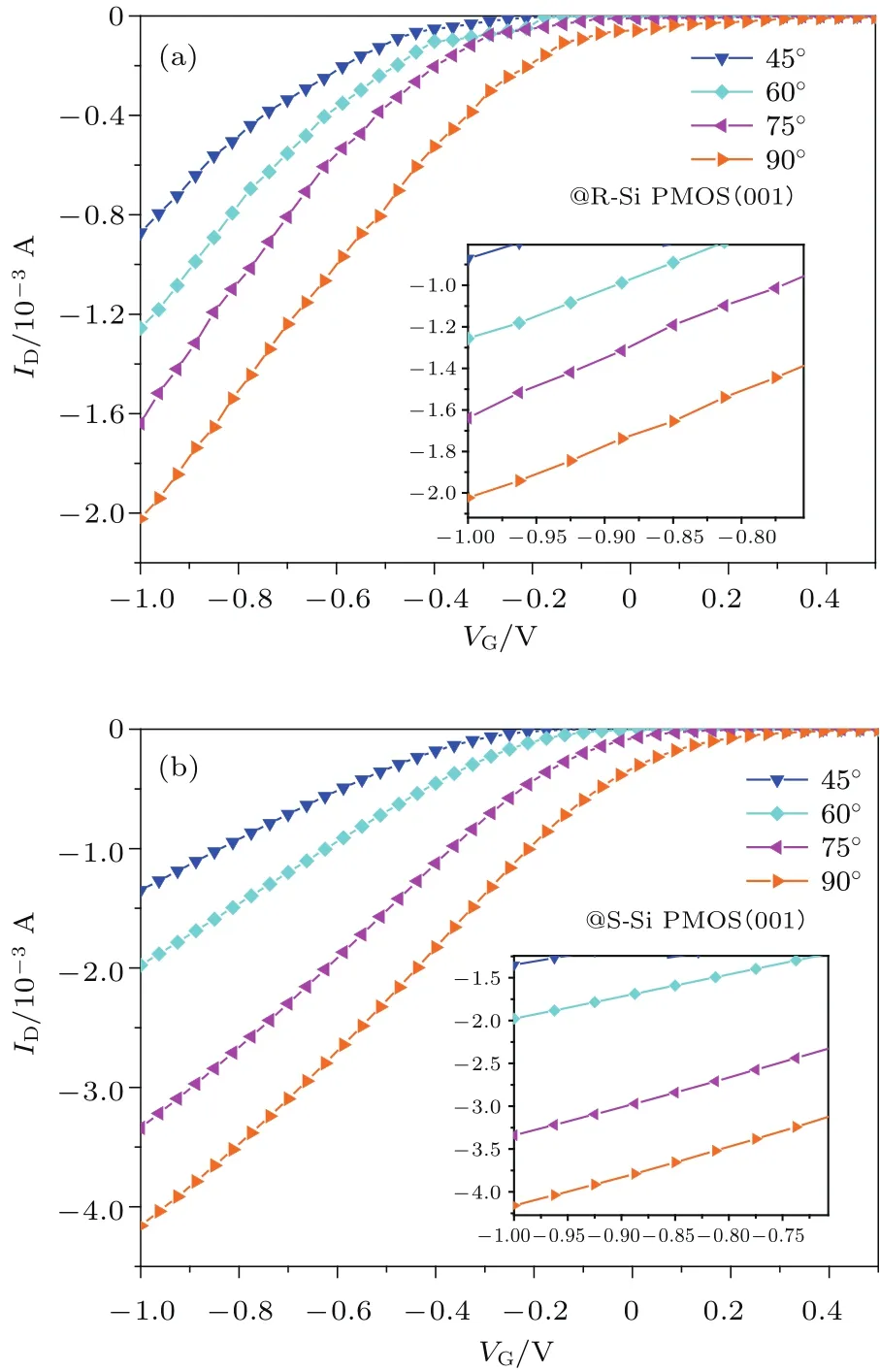
圖7 (001)晶面轉移特性曲線 (a)弛豫情況;(b)單軸應力作用Fig.7.Transfer characteristic curve of(001)crystal plane:(a)Relaxation;(b)uniaxial strained.

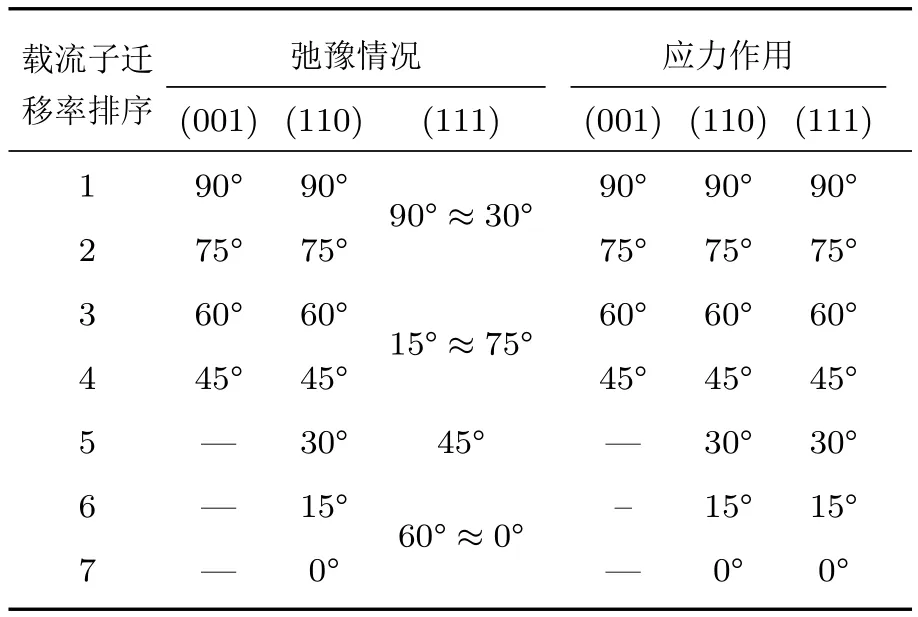
表1 不同晶面/晶向反型層載流子遷移率排序表Table 1.Sort table of inversion layer mobility on different crystal planes/orientation.

結合圖7(a)與圖8可以得出:弛豫情況下PMOS溝道角度從45°至90°的轉向過程中,漏極電流逐漸增大,即對應載流子遷移率逐漸增大.弛豫情況下(001)晶面反型層等能圖如圖9(a),[110]晶向對應溝道角度為45°的PMOS空穴有效質量最大,其載流子遷移率最小;[100]晶向對應溝道角度為90°的PMOS空穴有效質量最小,其載流子遷移率最大.但由于考慮等能圖為雙橢球模型[19],故[110]晶向與[010]晶向載流子有效質量雖有差距,但差距不大,因而弛豫情況下載流子遷移率排序與理論報道差距不大.

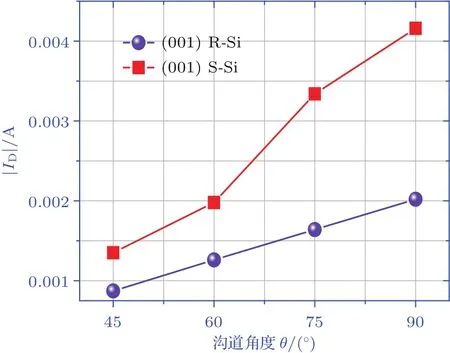
圖8 ?1 V柵壓下(001)晶面弛豫與應力作用下漏極電流與溝道角度的關系Fig.8.Relationship between drain current and channel angel under the in fl uence of relaxation or stress on(001)crystal plane at?1 V gate voltage.

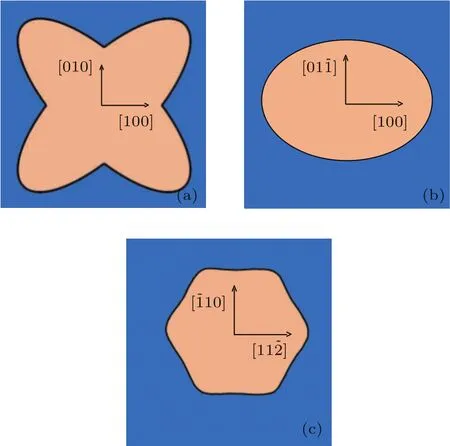
圖9 弛豫情況下不同晶面反型層等能圖 (a)(001);(b)(110);(c)(111)Fig.9. Equal-energy surfaces of different crystal planes of inversion layer under the in fl uence of relaxation:(a)(001);(b)(110);(c)(111).

結合圖7(b)與圖8可以得出:壓應力作用下,(001)晶面載流子遷移率排序與弛豫情況下的排序相同,仍為90°最高,45°最低;但是不同角度載流子遷移率較弛豫情況下有很大提升,增強倍數各不相同,90°時增強倍數最高,45°增強倍數最小,這是由于Si材料彈性勁度系數具有各向異性,在同種工藝淀積SiN應力膜時,不同晶向溝道上所反映出的應力大小各不相同.

圖10為弛豫情況與壓應力作用下(110)晶面不同角度的PMOS轉移特性曲線,通過對轉移特性曲線的提取分析可知:弛豫情況與應力作用下(110)晶面隨著角度的遞增,其漏電流逐漸增大,柵壓為?1 V時的不同溝道角度的漏極電流大小如圖11,進而可得到(110)晶面不同晶向反型層載流子遷移率的排序如表1.

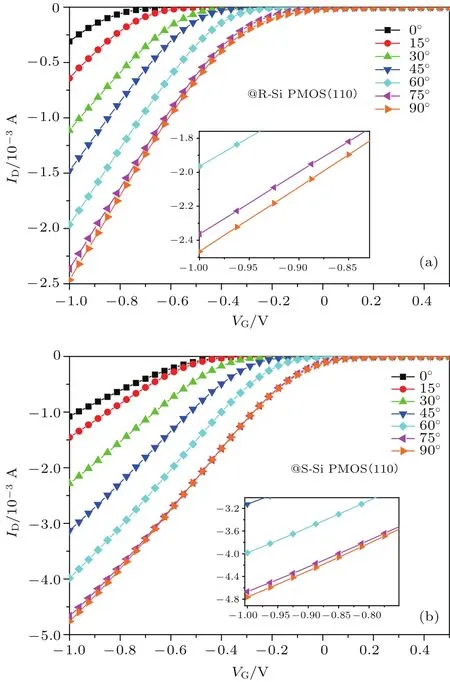
圖10 (110)晶面轉移特性曲線 (a)弛豫情況;(b)單軸應力作用Fig.10.Transfer characteristic curve of(110)crystal plane:(a)Relaxation;(b)uniaxial strained.

圖11 ?1 V柵壓下(110)晶面弛豫與應力作用下漏極電流與溝道角度的關系Fig.11.Relationship between drain current and channel angel under the in fl uence of relaxation or stress on(110)crystal plane at?1 V gate voltage.

圖12為弛豫情況與壓應力作用下(111)晶面不同角度的PMOS轉移特性曲線,通過對轉移曲線提取分析,獲得柵壓為?1 V時的不同溝道角度的漏極電流大小如圖13,進而可得到(111)晶面不同晶向反型層載流子遷移率的排序如表1.

結合圖12(a)與圖13可以得出:弛豫情況下,(111)晶面90°與30°晶向其漏電流大小接近,15°與75°晶向漏電流大小接近,0°與60°晶向漏電流大小接近,進而得出90°與30°晶向反型層載流子遷移率大小接近,15°與75°次之,45°較小,0°與60°最小.通過對比(111)晶面弛豫情況下的反型層等能圖,如圖9(c),可以得出0°與60°晶向、15°與75°晶向、30°與90°晶向為對稱晶向,其載流子有效質量相同,則理論上其載流子遷移率相同,與本文實驗中得到的結論相符,亦與理論報道相接近.從(111)晶面弛豫情況下的反型層等能圖還可以發現各個晶向載流子有效質量相差不大,所以各個晶向載流子遷移率不會有大的差距.進而得到弛豫情況下(111)晶面 [10]晶向載流子遷移率稍大于 [11]晶向載流子遷移率.

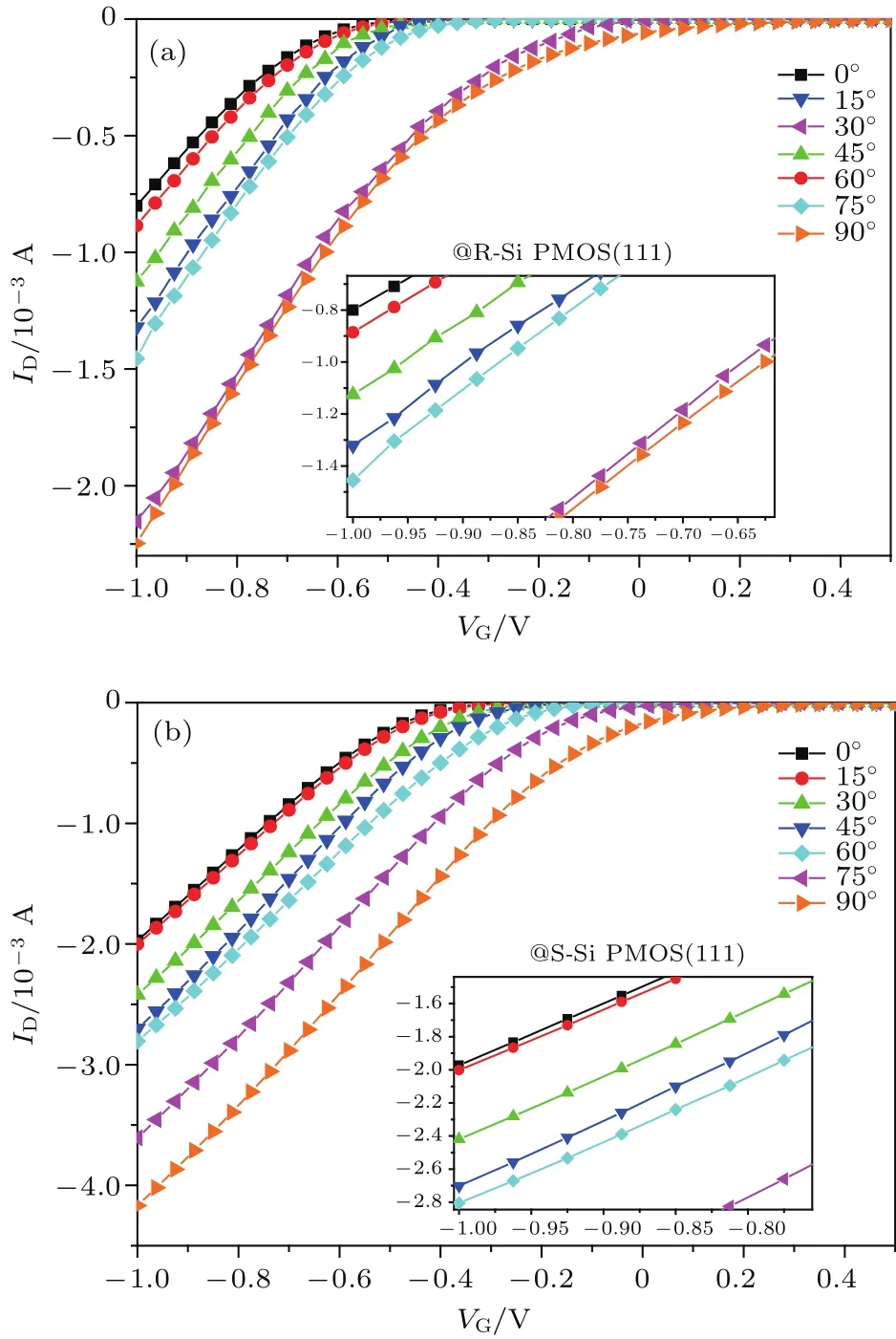
圖12 (111)晶面轉移特性曲線 (a)弛豫情況;(b)單軸應力作用Fig.12.Transfer characteristic curve of(111)crystal plane:(a)Relaxation;(b)uniaxial strained.

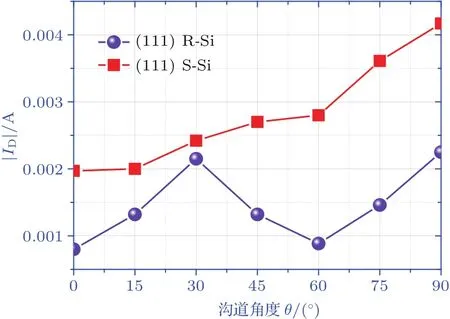
圖13 ?1 V柵壓下(110)晶面弛豫與應力作用下漏極電流與溝道角度的關系Fig.13.Relationship between drain current and channel angel under the in fl uence of relaxation or stress on(111)crystal plane at?1 V gate voltage.

結合圖12(b)與圖13可以得出:壓應力作用下,從0°到90°晶向的轉動過程中,漏電流逐漸增加,即相應載流子的遷移率逐漸增加,90°對應的[10]晶向載流子遷移率最大,0°對應的 [11]晶向載流子遷移率最小.與理論上的排序結果不符,主要原因在于應力作用下,由于其彈性勁度系數具有各向異性,所以在(111)晶面上不同晶向所對應的溝道上所受的應力并不相同,[10]晶向溝道所受的壓應力相對其他晶向的大,而[11]晶向溝道所受的壓應力最小.但是在理論分析過程中默認在(111)晶面上不同晶向所對應的溝道所受應力大小相等.

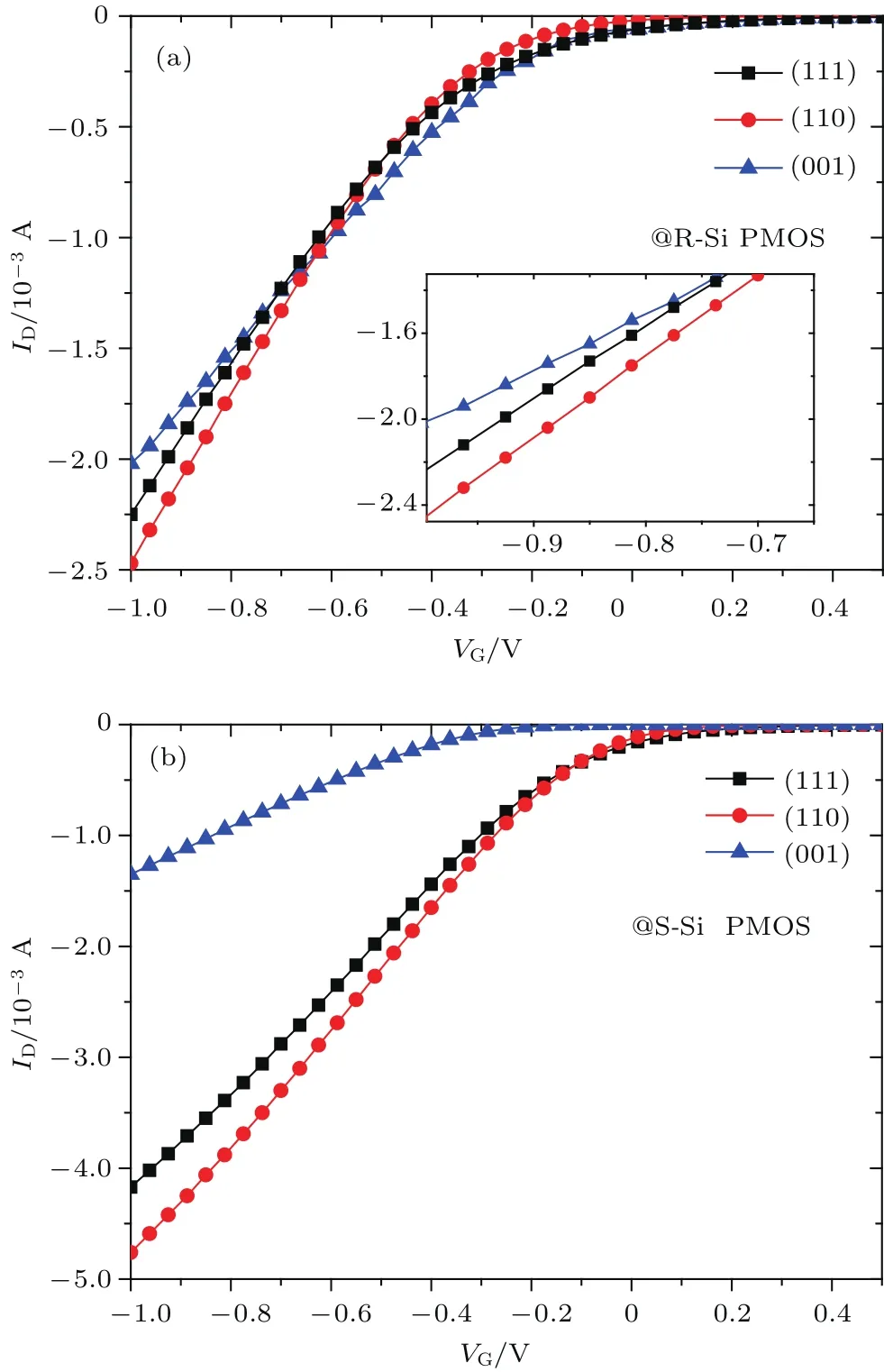
圖14 90°溝道下不同晶面轉移特性曲線 (a)弛豫情況;(b)單軸應力作用Fig.14.Transfer characteristic curve of 90°channel on different crystal planes:(a)Relaxation;(b)uniaxial strained.

在之前的討論中可以得到,弛豫與壓應力情況下,溝道角度為90°時對應不同晶面的最大遷移率.通過比較不同晶面90°溝道下的轉移特性曲線,如圖14,可以得出:弛豫情況下載流子遷移率排序為(110)＞(111)＞(001),載流子遷移率最大值出現在(110)晶面的90°溝道下;應力作用下,載流子遷移率排序為(110)＞(111)＞(001),載流子遷移率最大值同樣出現在(110)晶面的90°溝道下,即在壓應力條件下最大遷移率為(110)晶面的[10]晶向上.

通過在同一工藝下對實驗所制備的小尺寸壓應力下Si PMOS進行測試,得到實驗與理論情況下,壓應力作用時不同晶面反型層載流子遷移率排序對比表如表2,可以看出,實驗情況與理論分析有些許出入,這主要是由于晶體的彈性勁度系數具有各向異性,在同一實驗環境下,淀積相同的SiN應力膜時,不同晶向溝道上所反映出的壓應力大小不同.

為進一步說明實驗結果,采用(001)晶面不同晶向的器件進行反型層載流子遷移率的驗證,通過計算得到弛豫情況下,(001)晶面90°方向,即[100]晶向,載流子遷移率約為82 cm2/(V·s);而(001)晶面45°方向,即[110]晶向,載流子遷移率約為80 cm2/(V·s).這與理論情況相接近,文獻[15]理論報道中弛豫情況下(001)晶面不同晶向反型層載流子遷移率大小一致,約為87 cm2/(V·s).

表2 應力作用下PMOS反型層載流子遷移率對比Table 2.Comparative table of inversion layer mobility of Si PMOS under stress.

應力作用下,實際測得(001)晶面90°方向,即[100]晶向,載流子遷移率約為136 cm2/(V·s);而(001)晶面45°方向,即[110]晶向,載流子遷移率約為115 cm2/(V·s).[100]晶向反型層載流子遷移率增強幅度約為1.66倍,[110]晶向反型層載流子遷移率增強幅度約為1.44倍,這與文獻[15]結果相差較大,其原因在于文獻[15]中采用了1.5 GPa單軸應力,而在實際工藝中利用氮化硅膜無法引入這么大的應力,并且晶體彈性勁度系數具有各向異性,使得文獻[15]結果與實驗結果具有不統一之處,因此結果合理.

4 結 論

本文通過實驗系統驗證了小尺寸單軸應變Si PMOS不同晶面/晶向載流子的遷移率變化,并與理論相對比,得出了在工業制造中的具體情況下不同晶面/晶向載流子的遷移率排序.

在本實驗工藝條件下,小尺寸單軸應變Si PMOS反型層載流子遷移率排序表面上與理論計算看似不統一.一方面是由于理論計算時設定不同晶面、不同晶向所受到的壓應力大小相同,均為1.5 GPa,而在工業生產中應變PMOS器件中引入的壓應力大小為1.0 GPa,無法引入1.5 GPa的壓應力;另一方面是由于晶體存在彈性勁度系數矩陣,因此對于Si晶體而言其彈性勁度系數具有各向異性,當使用同一工藝淀積SiN應力膜時,不同晶向溝道上所反映出的應力大小將會有所不同,而這將會導致不同晶向上載流子遷移率的增強倍數各不相同,因此產生了實驗結果與理論分析不統一的情況.

本文實驗情況由于考慮到實際工藝的影響,給出了所有晶面/晶向的反型層載流子遷移率排序,所得出的反型層載流子遷移率新排序可為實際器件的制造提供具有指導性的參考,同時為其他應變材料的分析提供了一種新的思路.

[1]Guan H,Guo H 2017Chin.Phys.B26 058501

[2]Theerani J T 2017IEEE Trans.Electron Dev.64 3316

[3]Bai M,Xuan R X,Song J J,Zhang H M,Hu H Y,Shu B 2015Comput.Theor.Nanos12 1610

[4]Hao M R,Hu H Y,Liao C G,Wang B,Zhao X H,Kang H Y,Su H,Zhang H M 2017Acta Phys.Sin.66 076101(in Chinese)[郝敏如,胡輝勇,廖晨光,王斌,趙小紅,康海燕,蘇漢,張鶴鳴2017物理學報66 076101]

[5]Song J J,Yang C,Zhu H,Zhang H M,Xuan R X,Hu H Y,Shu B 2014Acta Phys.Sin.63 118501(in Chinese)[宋建軍,楊超,朱賀,張鶴鳴,宣榮喜,胡輝勇,舒斌2014物理學報63 118501]

[6]Liu W F,Song J J 2014Acta Phys.Sin.63 238501(in Chinese)[劉偉峰,宋建軍 2014物理學報 63 238501]

[7]Lee C H,Southwick R G,Bao R,Mochizuki S,Paruchuri V,Jagannathan H 2017Symposia on VLSI TechnologyKyoto,Japan,June 5–8,2017 p126

[8]Li L,Liu H X,Yang Z N 2012Acta Phys.Sin.61 166101(in Chinese)[李立,劉紅俠,楊兆年 2012物理學報 61 166101]

[9]Kasim J,Reichel C,Dilliway G,Bai B,Zakowsky N 2015Solid-State Electronics110 19

[10]Huang H L,Chen J K,Houng M P 2013Solid-State Electron.79 31

[11]Wang X Y 2012Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)[王曉艷 2012博士學位論文 (西安:西安電子科技大學)]

[12]Dai X Y,Yang C,Song J J,Zhang H M,Hao Y,Zheng R C 2012Acta Phys.Sin.61 137104(in Chinese)[戴顯英,楊程,宋建軍,張鶴鳴,郝躍,鄭若川2012物理學報61 137104]

[13]Wang G Y,Song J J,Zhang H M,Hu H Y,Ma J L,Wang X Y 2012Acta Phys.Sin.61 097103(in Chinese)[王冠宇,宋建軍,張鶴鳴,胡輝勇,馬建立,王曉艷2012物理學報61 097103]

[14]Zhang W H,Li Z C,Guan Y H,Zhang Y F 2017Chin.Phys.B26 078502

[15]Krishnamohan T,Kim D,Dinh T V,Pham A,Meinerzhagen B,Jungemann C,Saraswat K 2008Electron Devices MeetingSan Francisco,CA,USA,December 15–17,2008 p1

[16]Cai W L,Takenaka M,Takagi S 2014J.Appl.Phys.115 094509

[17]Yang M Y,Song J J,Zhang J,Tang Z H,Zhang H M,Hu H Y 2015Acta Phys.Sin.64 238502(in Chinese)[楊旻昱,宋建軍,張靜,唐召喚,張鶴鳴,胡輝勇 2015物理學報64 238502]

[18]Song J J 2008Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)[宋建軍 2008博士學位論文 (西安:西安電子科技大學)]

[19]Song J J,Bao W T,Zhang J,Tang Z H,Tan K Z,Cui W,Hu H Y,Zhang H M 2016Acta Phys.Sin.65 018501(in Chinese)[宋建軍,包文濤,張靜,唐昭煥,譚開洲,崔偉,胡輝勇,張鶴鳴2016物理學報65 018501]