切觸有理插值新方法
經慧芹
(昆明理工大學成人教育學院,云南 昆明 650051)
1 引言
有理插值就是根據已知的點和函數值構造一個有理函數代替未知函數,并使所構造的函數在已知點處的值等于預定的值.帶導數條件的有理插值稱為切觸有理插值,切觸有理插值應用廣泛,可應用于現代力學的諸多領域,還應用于圖像處理[1-3]、機械、建筑、航空航天、艦船、醫學等領域的曲線或曲面造型[4-8].切觸有理插值的傳統方法是連分式,具體計算時需要把已知節點、函數值和導數值代入固定格式循環迭代,不僅計算量大,而且在計算過程中有時會出現分母為零或者插值函數不滿足某些插值條件的情況.解決的方法是:把使得分母為零的節點調整至插值點列的最后,從頭再來計算[9-10];在不滿足插值條件之點處定義另一個插值函數[11],或者增加不滿足條件的節點重數[12].這些方法雖然解決了一定的問題,但更增大了計算量,應用不便.近年來又相繼出現了一些構造切觸有理插值函數的方法,如用分段組合和牛頓插值多項式構造[13],用埃米特基函數構造[14],用Taylor算子構造[15].這些方法雖好,但計算復雜度高的問題仍未得到有效解決.本文給出了完全不同于以上各種方法的一類切觸有理插值的新方法,該方法所構造的插值函數,其分母在已知節點處不為零,滿足所有插值條件,計算簡單,過程公式化,應用很方便.
2 預備知識
定義 2.1若?P(x)≤m,?Q(x)≤h,則稱有理函數的次數類型為[m|h]型,記

其中?表示多項式次數.
定義 2.2稱形如
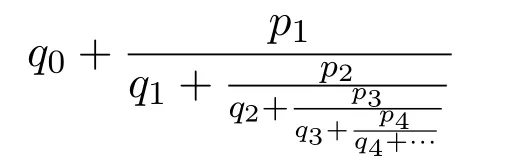
的分式為連分式,記作
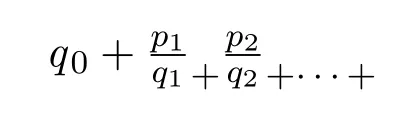
定義 2.3已知函數f(x),S={xp|p=0,1,2,···}為一個點集,令
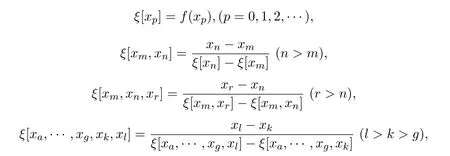
稱上述式子確定的ξ[x0,x1,···,xl]為函數f(x)在點x0,x1,···,xl處的l階逆差商.
定義 2.4稱連分式
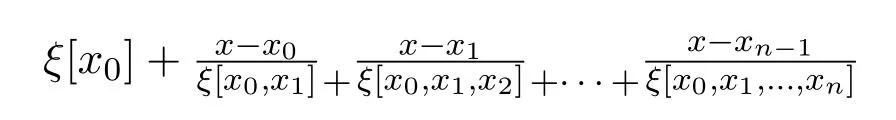
為逆差商-Thiele型連分式;稱連分式

為Salzer型切觸有理插值連分式.
定義 2.5已知插值節點x0<x1<···<xn及導數值所謂切觸有理插值就是尋求一個有理分式函數使得

其中

定義 2.6令
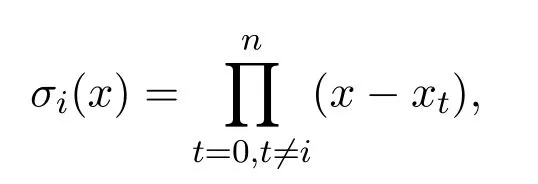
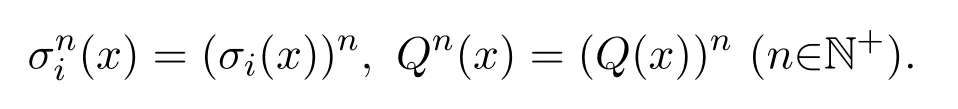
定義 2.7令
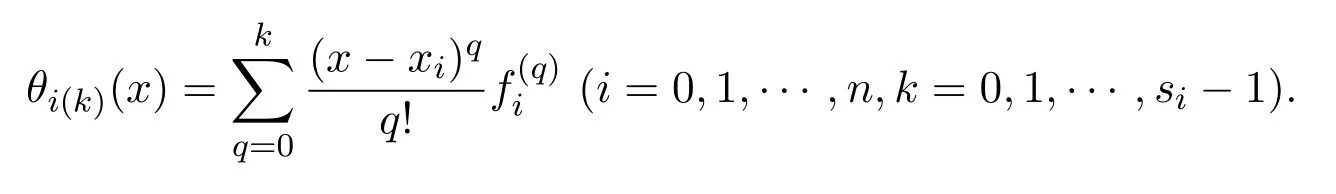
3 主要結論
定理 3.1已知插值節點x0<x1<···<xn及相應的函數值fi,則有理分式函數

滿足插值條件R(xi)=fi(i=0,1,···,n).
證明因為
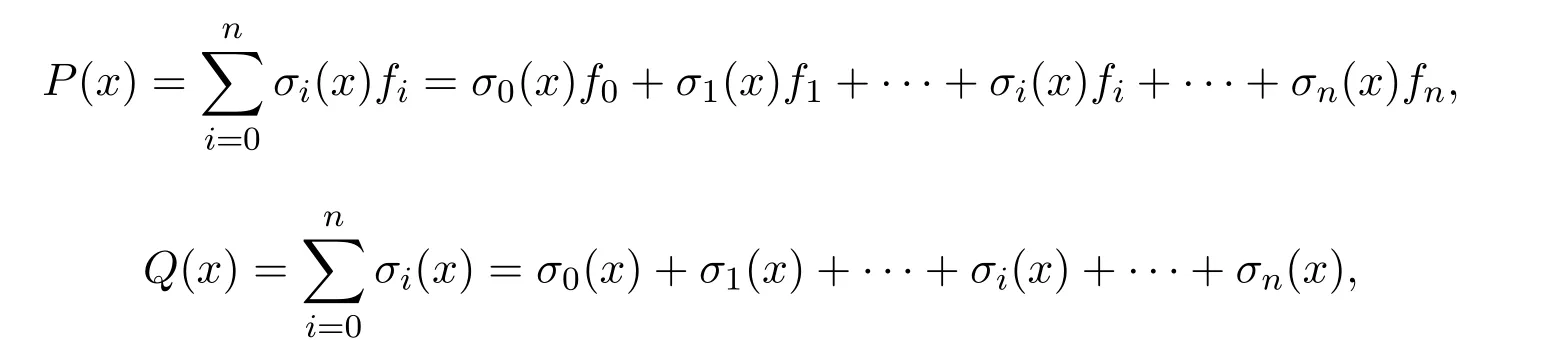
所以P(xi)=σi(xi)fi,Q(xi)=σi(xi),因此

定理 3.2已知插值節點x0<x1<···<xn及相應的函數值fi,一階導數值則有理分式函數:
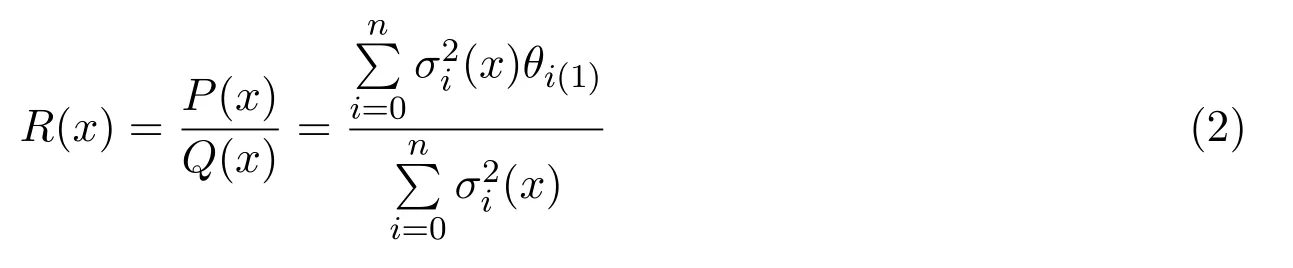
證明由定義2.7知,
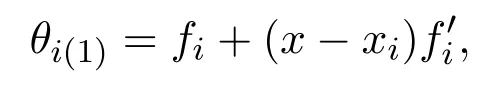
根據公式(2),
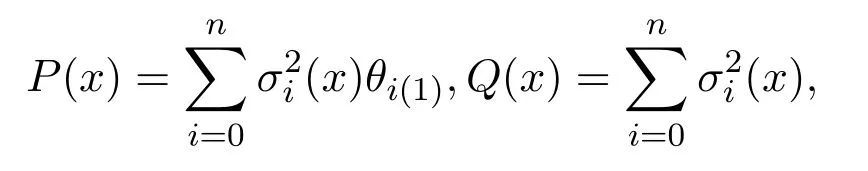
于是

從而
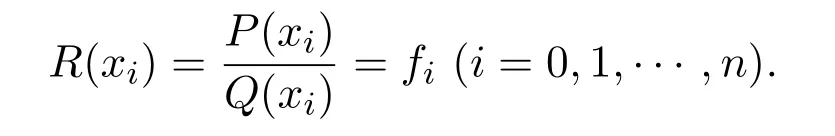
又因為

故

定理 3.3已知插值節點x0<x1<···<xn及相應的函數值fi,一階導數值二階導數值則有理分式函數
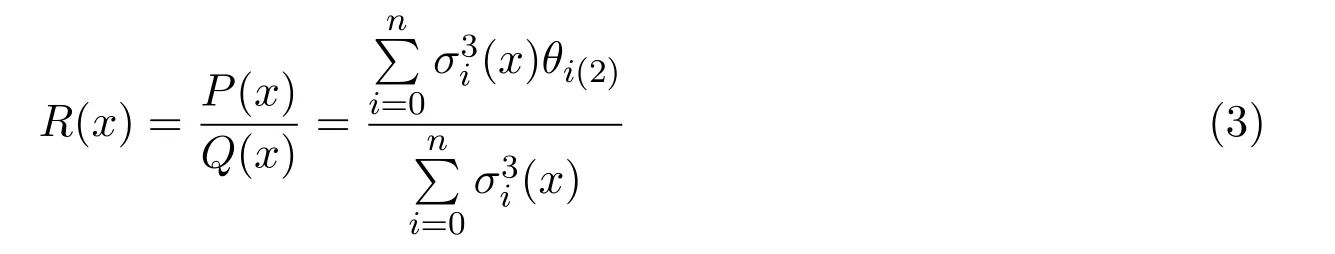
滿足插值條件

證明由定義2.7知,

根據公式(3),
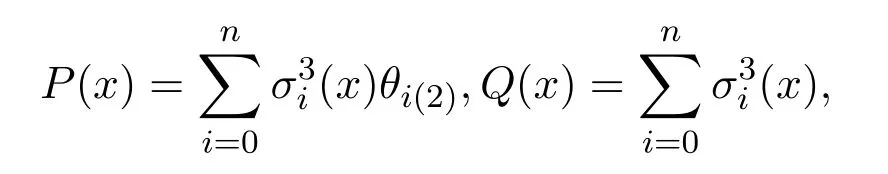
從而
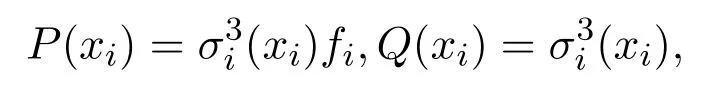
于是
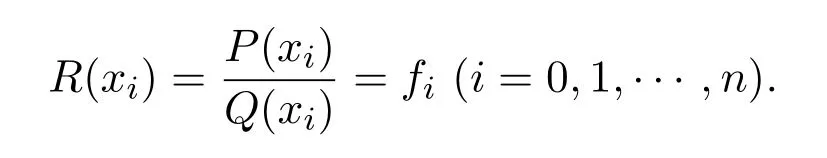
又因為
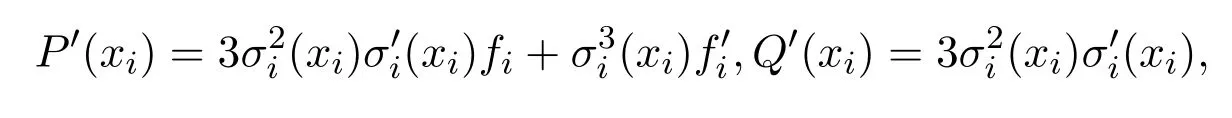
故
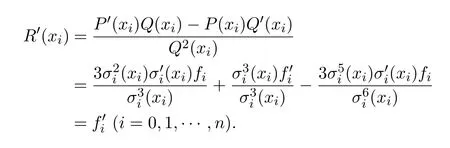
又
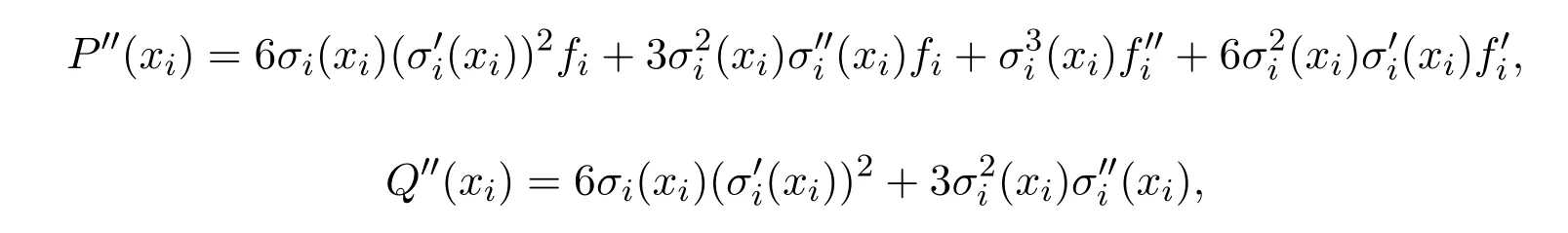
故

特例已知插值節點x0<x1<···<xn及相應的函數值fi,二階導數值則有理分式函數


滿足插值條件一般地,已知節點x0<x1<···<xn及函數值fi,一階導數值二階導數值階導數值則有理分式函數
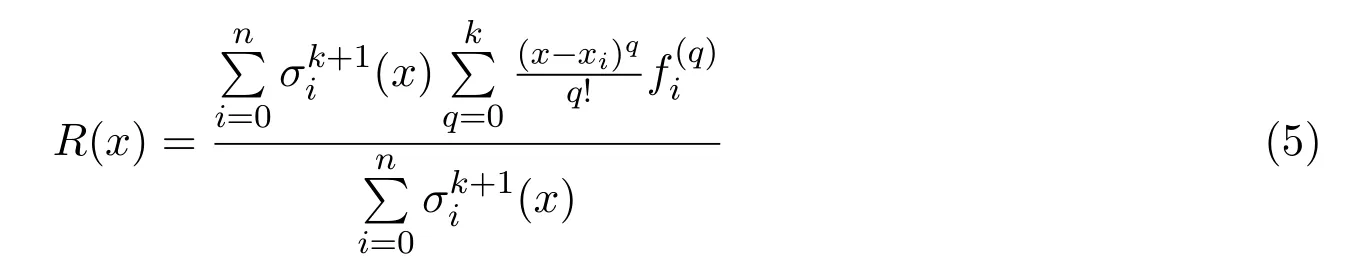
滿足插值條件
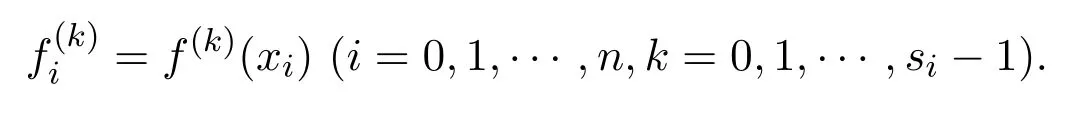
在(5)式中添加適當的參數ρi(i=0,1,···,n),可降低插值函數R(x)的次數,即
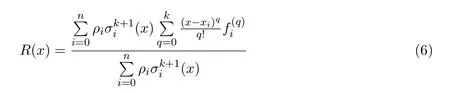
4 數值算例
例 4.1已知數據求有理函數使得

解法一(用本文的新方法)
根據公式(1),有理插值函數的分子P(x),分母Q(x)分別計算如下:

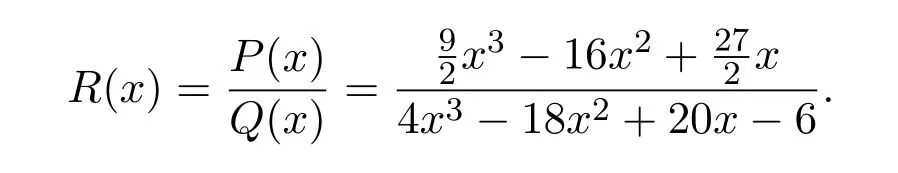
于是,插值函數經過檢驗所得有理插值函數R(x)滿足全部插值條件,即
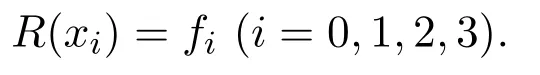
解法二(用逆差商-Thiele型連分式算法)
設所求有理函數為:
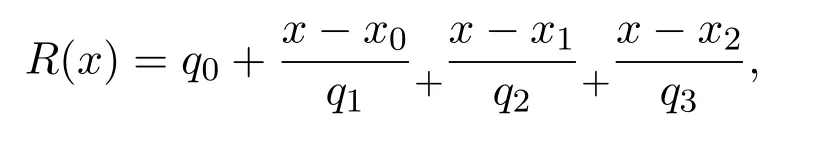
其中

計算q3時出現了分母為零,運算無法進行下去.
例 4.2已知函數f(x)=ex,插值節點x1=0,x2=1,求有理插值函數使得
解法一(用本文的新方法)
因為
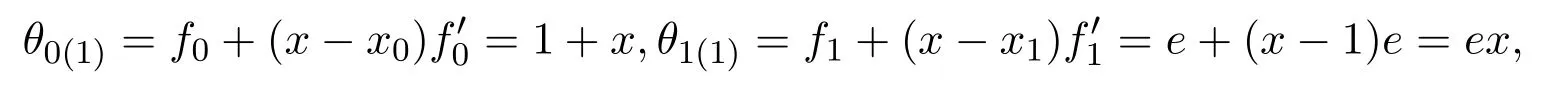
根據公式(2),
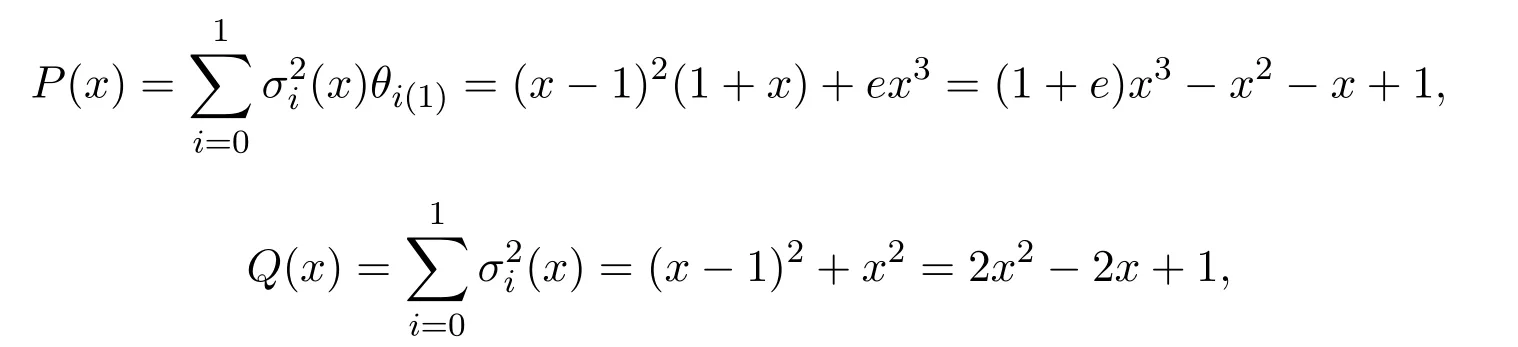
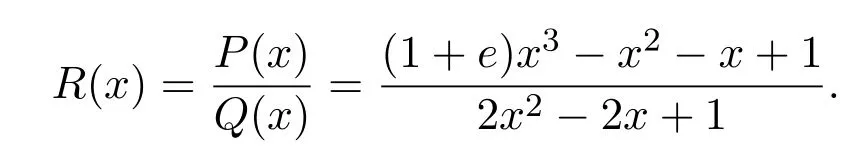
于是,插值函數經過檢驗所得有理插值函數R(x)滿足全部插值條件,即
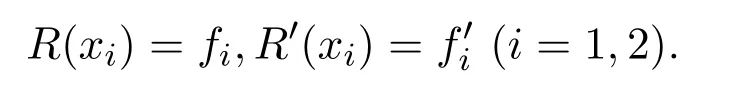
解法二(用Salzer型切觸有理插值連分式算法)
設插值函數

根據Salzer型連分式的系數算法,
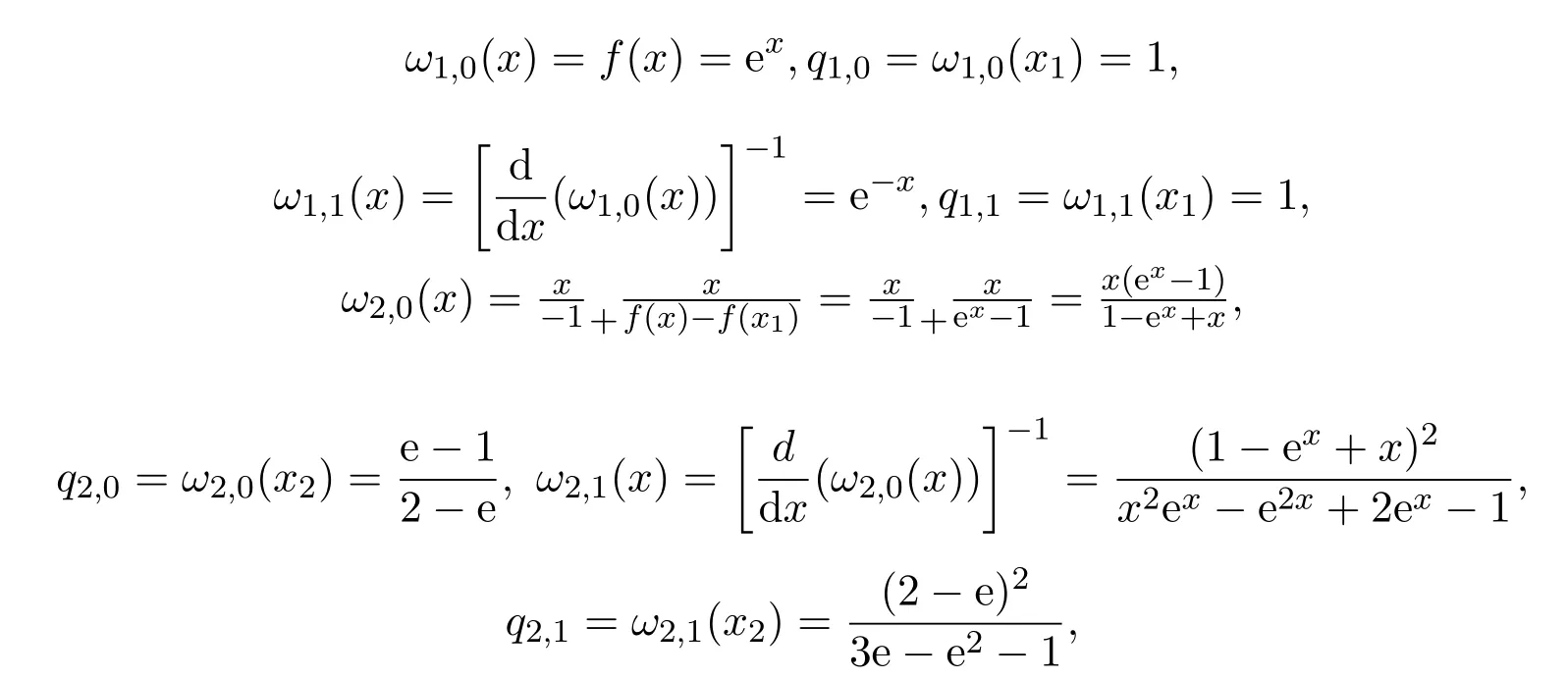
所以

經過檢驗R(x)滿足全部插值條件
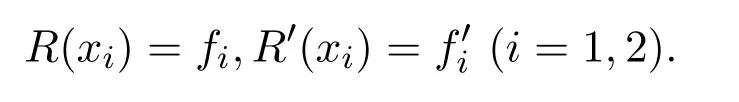
注 4.1①在例 4.2中,雖然用 Salzer型連分式算法求出了插值函數R(x),但前提是必須已知被插函數R(x).如果只知道幾個離散數據點及導數值,則無法計算連分式的系數q1,0,q1,1,q2,0,q2,1,也就無法應用連分式插值.
②本文的新方法無需知道被插函數,只要已知幾個數據點就可以求插值函數.由此可見,本文的新方法,不需要任何附加條件,它比連分式應用范圍更廣,功能更強,使用更方便.
③本文新方法比連分式算法簡單.
例 4.3已知求有理函數使得
解由于
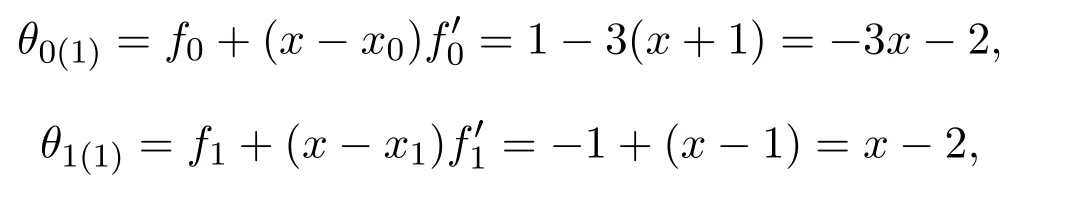
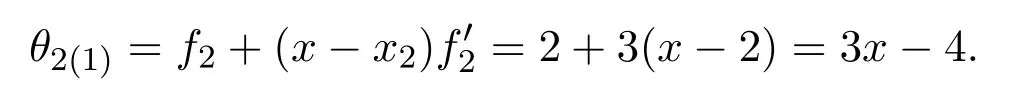
根據公式(2),
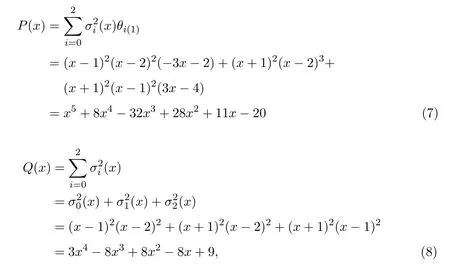
由 (7)、(8)兩式得

經過檢驗所得插值函數R(x)滿足全部插值條件,即
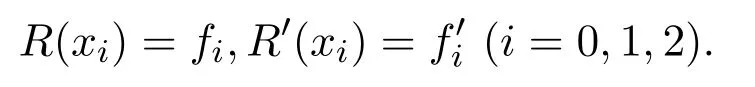
注 4.2①例三中因被插函數f(x)未知,所以用傳統的Salzer型連分式算法,無法計算;
②例三說明,本文的新方法比切觸有理插值的傳統Salzer型連分式算法適用面更廣,只要知道了數據點及相應的導數值,用本文的新方法都能簡單、順利地進行運算.
下面引進參數ρi(i=0,1,2),將(9)式中分母Q(x)的次數降低.
令有理插值函數為:
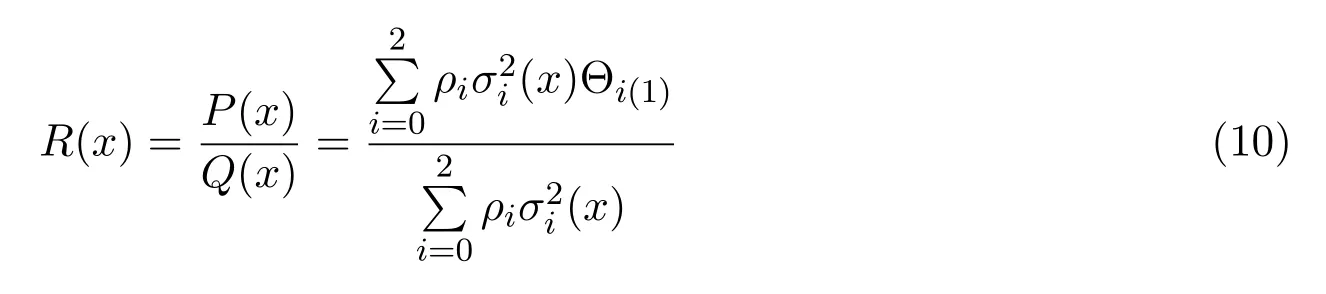
則
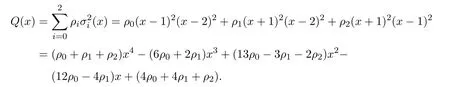
若要把Q(x)的次數降低2次,只要解方程組
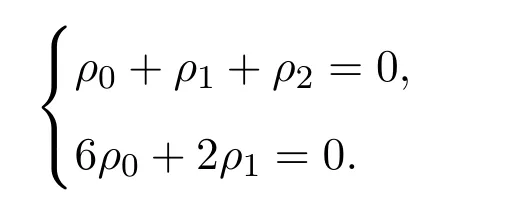
該方程組有非平凡解,取ρ0=1,ρ1=?3,ρ2=2為其解.
此時

并且
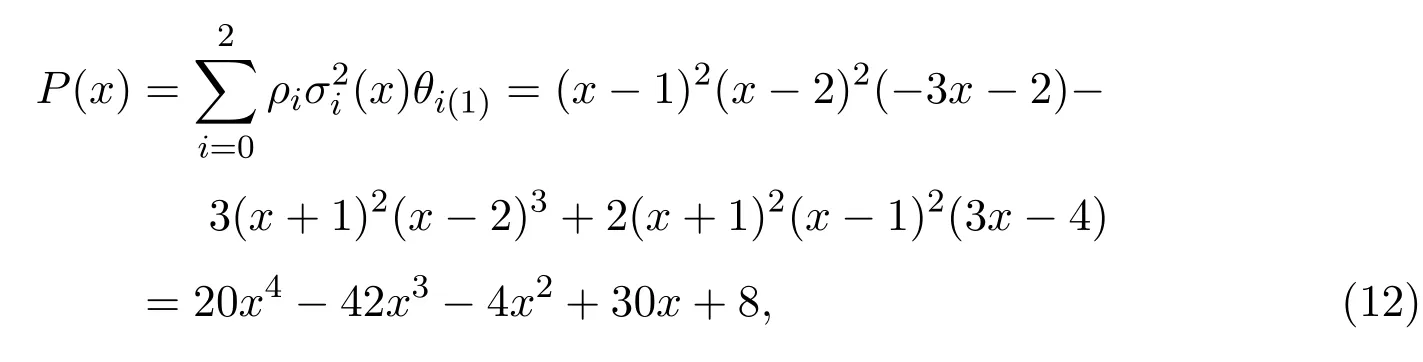
由 (11)、(12)兩式得
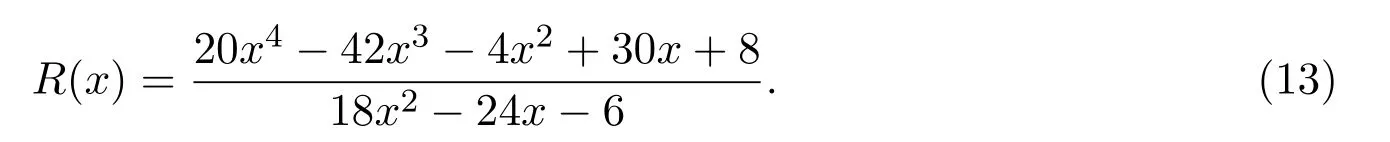
經過檢驗,(13)式的插值函數R(x)仍然滿足

5 結束語
切觸有理插值的應用非常廣泛,從工業產品的外形設計到現代醫學的3D打印等都有所涉及.因此,探究簡單方便的插值方法顯得尤為重要.本文方法是構造性的,計算復雜度低,實際應用方便,并且有效克服了傳統連分式插值的缺陷,使任意階導數的有理插值變得可行且容易,具有應用前景,創新點如下:
(1)構造了各階導數有理插值新公式,計算簡單,無需附加條件;
(2)插值函數的分母在節點處不等于零,運算始終能順利進行,且滿足全部插值條件;
(3)添加參數可降低插值函數的次數.
[1]Su Benyue,Sheng Min.Adaptive algorithm for image interpolation based on blending osculatory rational interpolants[J].Computer Engineering and Applications,2010,46(1):196-199.
[2]Fan Qinglan,Zhang Yunfeng,Bao Fangxun.Rational function interpolation algorithm based on parameter optimization[J].Journal of Computer Aided Design Computer Graphics,2016,28(11):2034-2042.
[3]Ning Yang,Zhang Yunfeng,Gao Shanshan.Adaptive weighted interpolation based on rational function over triangular domain[J].Journal of Graphics,2015,36(3):444-451.
[4]Zhao Haiyang,Xu Minqiang,Wang Jindong.Local mean decomposition based on rational hermite interpolation and its application for fault diagnosis of reciprocating compressor[J].Journal of Mechanical Engineering,2015,51(1):83-89.
[5]Wang Zhaoqing,Zhang Meiling,Jiang Jian.Nonlinear mems microbeam analysis by barycentric rational interpolation iteration collocation method[J].Journal of Solid Mechanics,2015,36(5):453-459.
[6]Debbourgor.Accurate c2 rational interpolants in tension[J].Aiamj.Numer.Anal.,1993,2:595-607.
[7]Fang Kui,Deng Siqing,Tan Desong.Curves and surface of rational cubic interpolation spline[J].Computer Applications and Software,2011,28(7):22-24.
[8]Zhao Huanxi.Rational interpolation skinning surface via continued fractions interpolation based on partial generalized function inverse[J].Journal of System Simulation,2016,28(10):2497-2502.
[9]Floater M S,Hormann K.Barycentric rational interpolation with no poles and high rates of approximation[J].Numerische Mathematik,2007,107(2):315-331.
[10]Wang Renhong,Zhu Gongqin.Rational Function Approximation and its Application[M].Beijing:Science Press,2004:146-178.
[11]Zhu Gongqin,Tan Jieqing,Wang Hongyan.Algorithms and properties of vector valued rational interpolants with prescribed poles[J].Higher School Journal of Computational Mathematics,2000(2):97-104.
[12] Levrie P,Bultheel A.A note on thiele n-fractions numerical algorithms[J].Comput.Math.Appl.,2013,4:225-239.
[13]Jing Ke,Kang Ning.Rational interpolation algorithm with heredity[J].Computer Engineering and Applications,2016,52(3):202-205.
[14]Jing Ke,Liu Yezheng,Kang Ning.An algorithm of osculatory rational interpolation for high order derivative[J].Mathematica Applicata,2015,28(4):737-742.
[15]經慧芹.基于Taylor算子的二元向量切觸有理插值[J].應用數學和力學,2016,37(4):404-415.

