具反饋控制的一方不能獨立生存偏利合作系統的穩定性

楊英鐘,王寬程

(閩南理工學院信息管理學院,福建 泉州 362700)

1 引言

近年來,很多學者針對合作生態系統的持久性展開了研究,并得到了相應的研究成果[1-4].而有關偏利合作種群模型的研究工作還很少,祝占法等[5]提出了如下一方不能獨立生存的兩種群偏利合作模型:

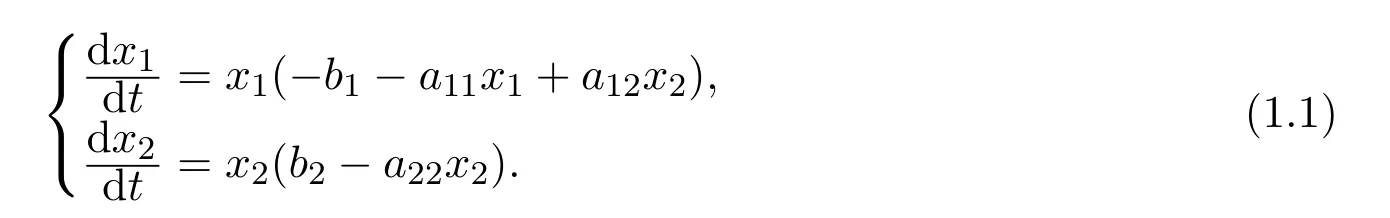
其中bi,aij,i,j=1,2均為正常數,xi,i=1,2是種群在t時刻的生長密度.作者借助向量場分析的方法得出當

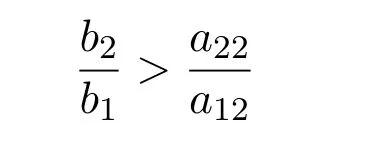
時,系統(1.1)存在唯一全局漸近穩定的正平衡點,并得出種群弱平均持續生存和絕滅的充分性條件.

另一方面,在現實生活中,考慮到生態系統會受到人類的干擾,為此,學者們引入了反饋控制變量.2016年,周曉燕等[6]提出如下具有反饋控制的單方不能獨立生存合作模型:

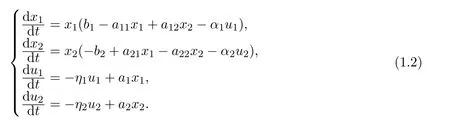
其中ui,i=1,2是反饋控制變量.在文獻[6]中,作者通過構造適當的Lyapunov函數,得到研究表明,在原系統存在唯一的全局漸近穩定的正平衡點時,引入適當的反饋控制變量,系統(1.2)仍具有唯一的全局漸近穩定的正平衡點;引入不適當的反饋控制變量,則不能獨立生存的第二種群終將絕滅.

注意到至今尚未有學者研究具反饋控制的一方不能獨立生存的偏利合作系統:

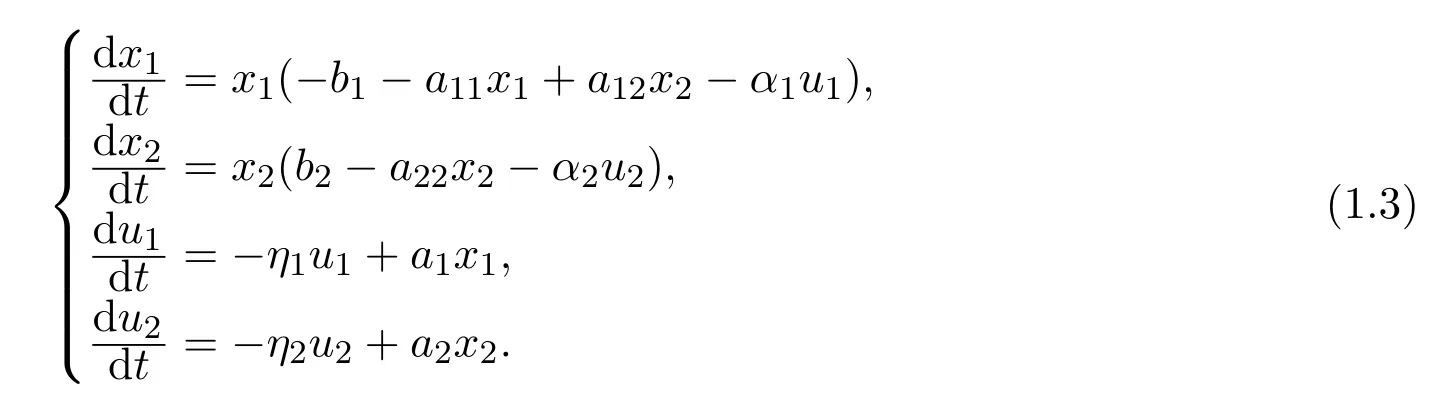
其中,系統(1.3)的所有參數ai,bi,aij,αi,ηi,i,j=1,2均為正常數,xi,i=1,2是種群在t時刻的生長密度,ui,i=1,2是反饋控制變量.其中第二種群對第一種群的生長起有利作用,而第一種群對第二種群的生長不起作用,而且第一種群不能獨立生存.本文旨在研究反饋控制變量對系統(1.3)正平衡點和邊界平衡點動力學行為的影響.

2 主要結果及其證明

計算易知當條件

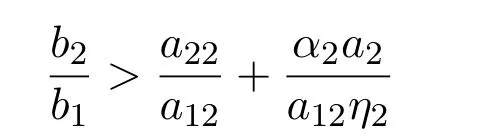
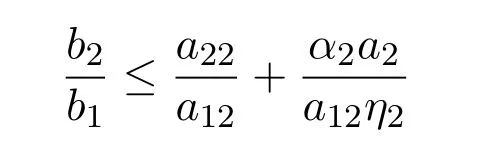
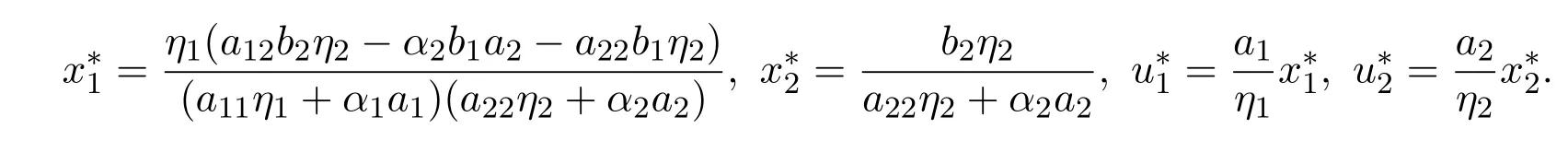
下面探討系統(1.3)平衡點的穩定性.

定理 2.1若

證明注意到滿足:

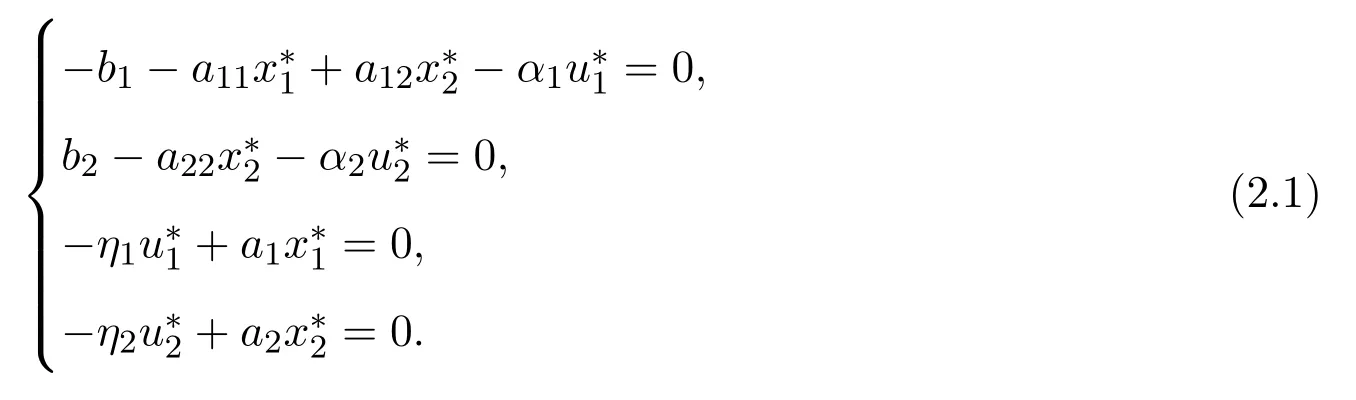
現構造Lyapunov函數:

其中λi,i=1,2,3,4是待定正常數.沿著系統(1.3)的正解計算V1(t)的導數,借助(2.1)可得:

令

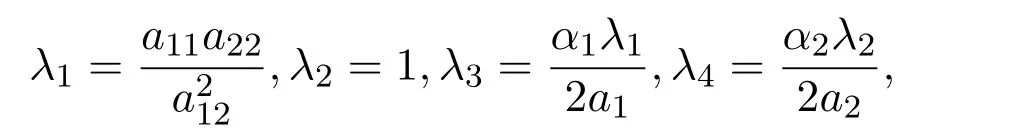
則有

因為a11λ1＞0,

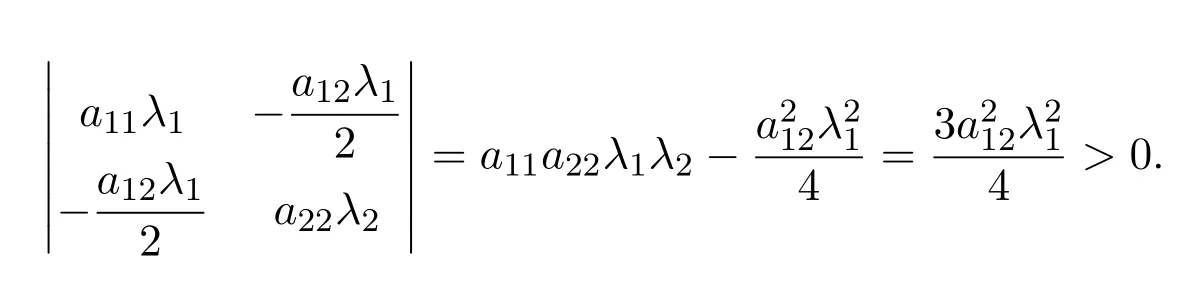
所以矩陣

是正定矩陣.

這表明

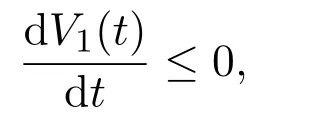
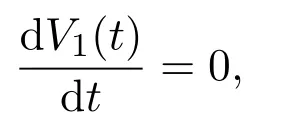
則由文獻 [7]的 Lyapunov穩定性定理可知,正平衡點是全局漸近穩定的.

注 2.1定理2.1表明對于一方不能獨立生存的偏利合作系統而言,在原系統(1.1)具有唯一的全局漸近穩定的正平衡點的情況下,反饋控制變量僅改變正平衡點的位置,使得種群的平衡密度發生改變,而不會改變正平衡點的穩定性.

定理 2.2若

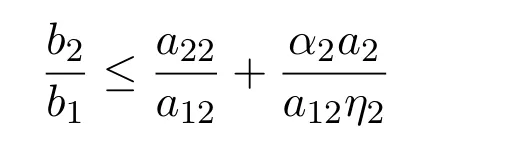
證明注意到滿足:

現構造Lyapunov函數:

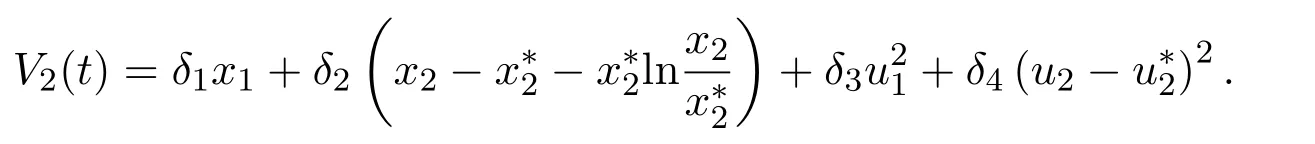
其中δi,i=1,2,3,4是待定正常數.沿著系統(1.3)的正解計算V2(t)的導數,借助(2.2)可得:

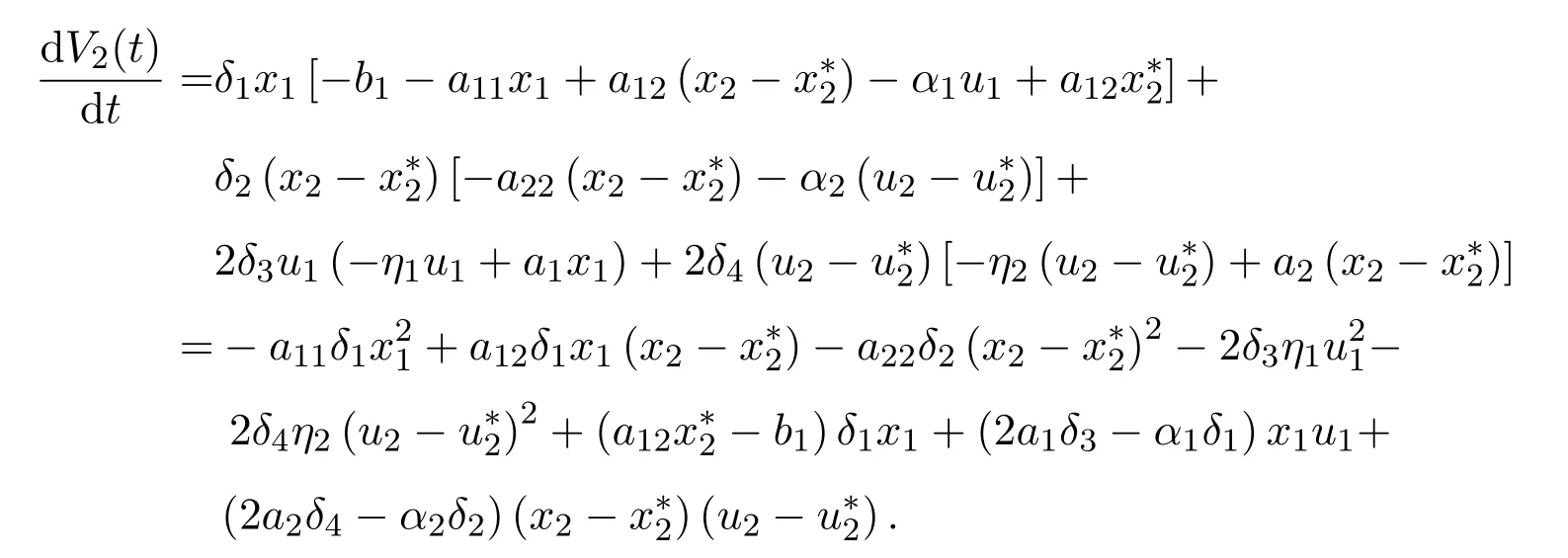
令

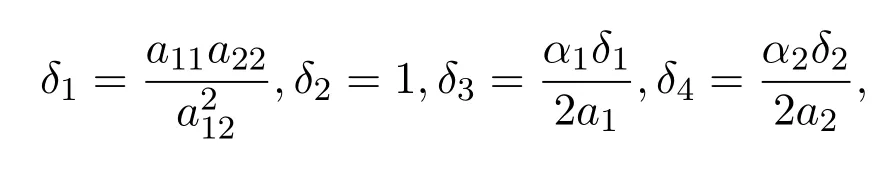
則有

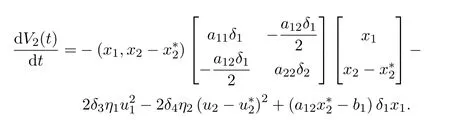
因為a11δ1＞0,

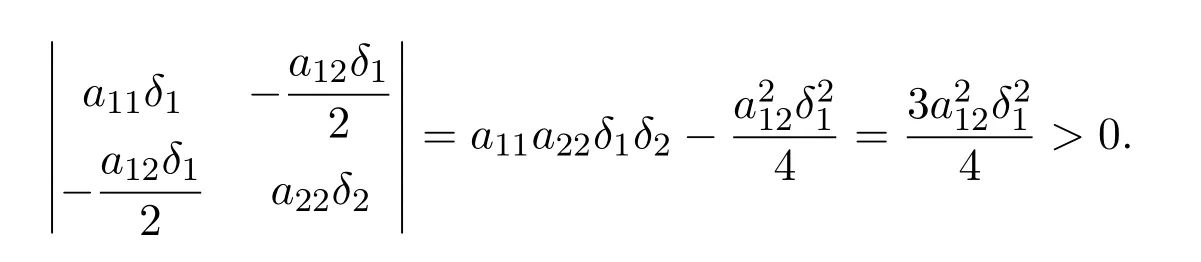
所以矩陣

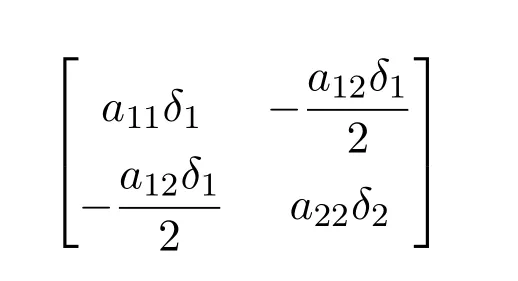
是正定矩陣.

又因為當

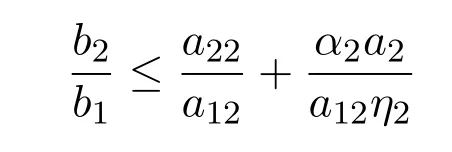
時,

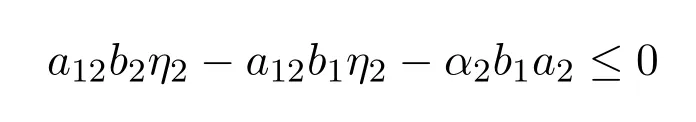
成立.所以

這表明

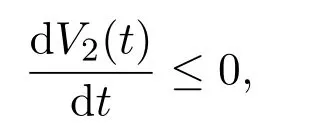
當且僅當x1=0,x2=x?2,u1=0,u2=u?2時,

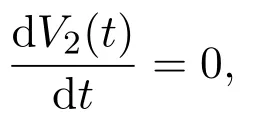
注 2.2當

時,原系統(1.1)存在唯一的全局漸近穩定的正平衡點,但加入反饋控制變量后,系統(1.3)只存在唯一穩定的邊界平衡點,這時不能獨立生存的第一種群將最終走向滅絕.這表明不當的人類干擾反而不利于系統中生物種群的生長.

注 2.3值得注意的是,定理2.1和定理2.2的條件只含有跟第二個反饋控制變量u2有關的量a2和η2,而與u1無關.這說明第二個反饋控制變量u2影響系統(1.3)種群的生存,而第一個反饋控制變量u1與種群生存無關,僅影響種群的平衡密度.

3 數值模擬

以下通過具體的例子來驗證定理的可行性.

例 3.1考慮如下系統：

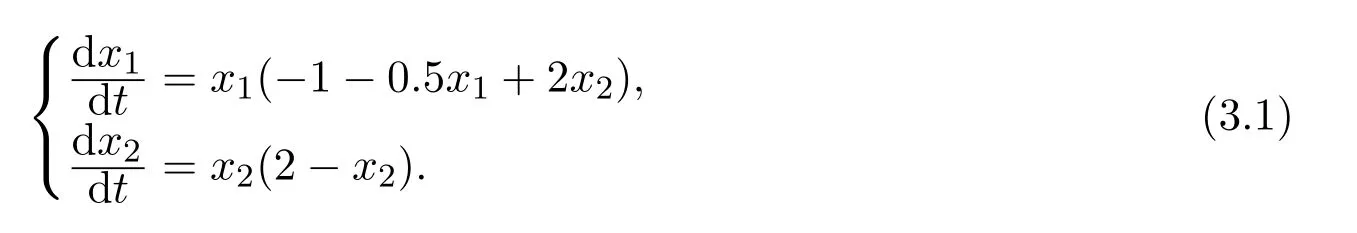
這里相對于系統(1.1),其中b1=1,b2=2,a11=0.5,a12=2,a22=1,則

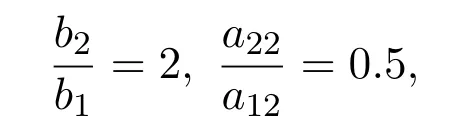
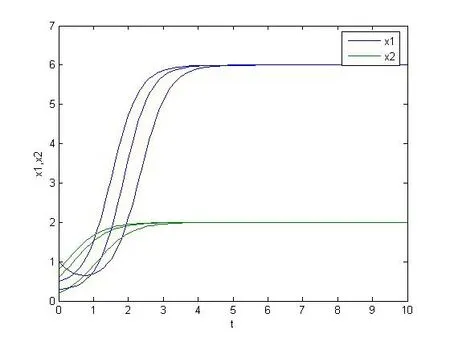
圖1 系統(3.1)的數值模擬圖

例 3.2考慮如下具有反饋控制變量的系統:

(1)滿足定理2.1的實例

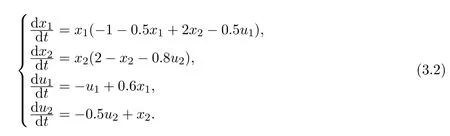
相對于例3.1,系統(3.2)增加系數

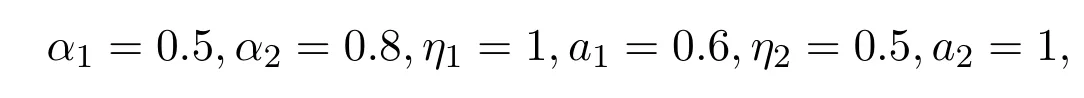
則

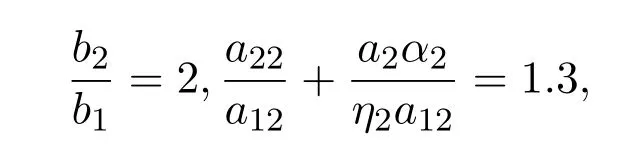
滿足定理2.1的條件

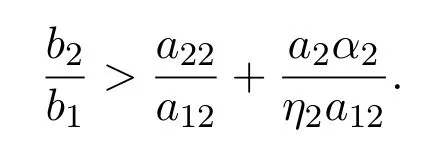
所以系統(3.2)存在唯一全局漸近穩定的正平衡點

系統(3.2)具有初值

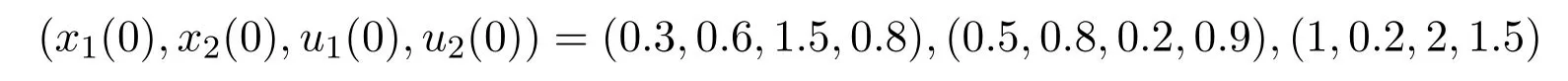
的解的數值模擬圖,如圖2所示:

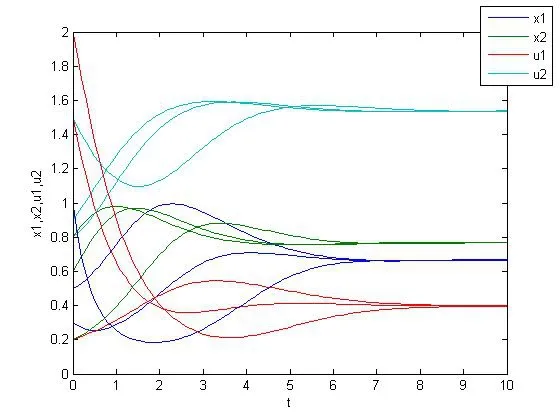
圖2 系統(3.2)的數值模擬圖

(2)滿足定理2.2的實例

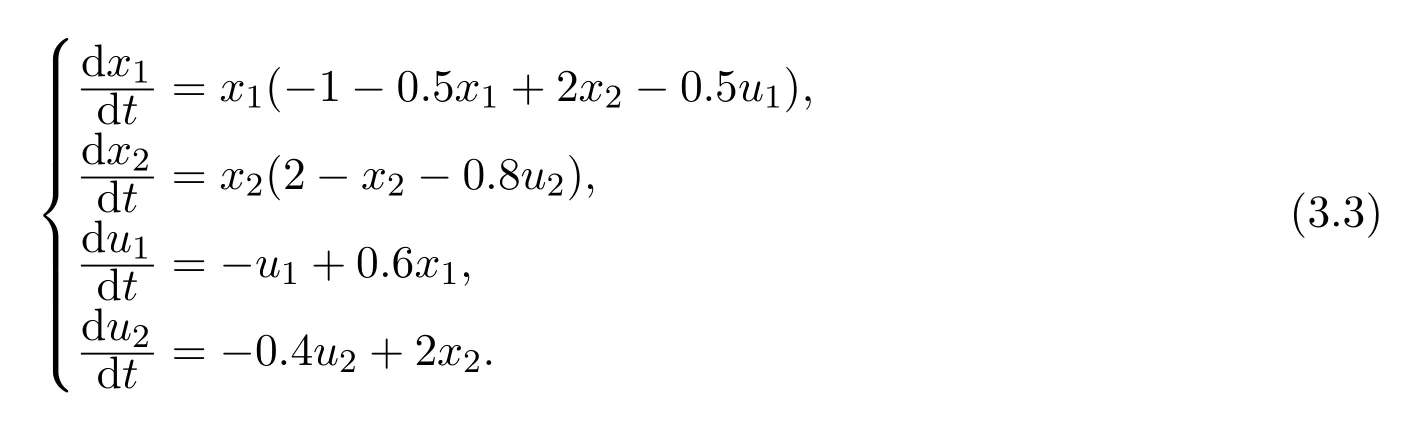
相對于系統(3.2),系統 (3.3)將η2和a2的值修改為η2=0.4,a2=2,則

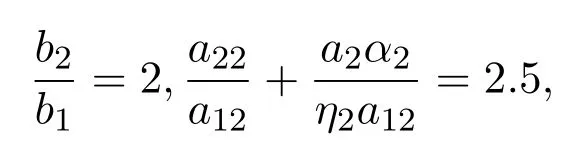
滿足定理2.2的條件

所以系統(3.2)存在全局漸近穩定的邊界平衡點P2(0,0.4,0,2).系統(3.3)具有初值的解的數值模擬圖,如圖3所示:

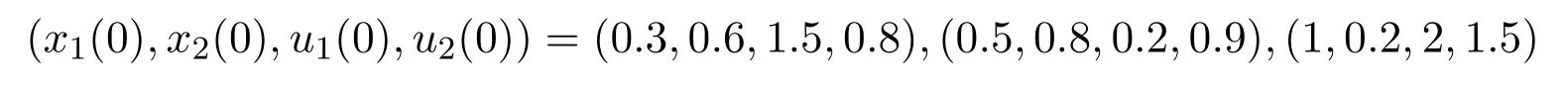
圖3 系統(3.3)的數值模擬圖

[1]趙亮,陳鳳德.具有反饋控制的競爭系統邊界平衡點的穩定性[J].北華大學學報,2013,14(5):516-519.

[2]楊坤,王海娜,陳鳳德.反饋控制Lotka-Volterra合作系統穩定性研究[J].應用數學,2014,27(2):243-247.

[3]陳鳳德,龔曉杰,普麗瓊,等.具有反饋控制的 Lotka-Volterra捕食 -食餌系統研究[J].生物數學學報,2015,30(2):328-332.

[4]黃宏韜,林錦賢.具有反饋控制變量的偏害模型穩定性研究[J].福州大學學報,2017,45(1):69-73.

[5]祝占法,粟永安,徐芳.具有偏利關系的Lotka-Volterra模型[J].重慶工學院學報(自然科學版),2007,21(10):59-62.

[6]周曉燕,普麗瓊,薛亞龍,等.具反饋控制的單方不能獨立生存合作系統穩定性研究 [J].應用數學學報,2016,39(2):298-305.

[7]陳蘭蓀,宋新宇,陸征一.數學生態學模型與研究方法[M].成都:四川科學技術出版社,2003.