基于等距映射的非線性系統集員參數估計

柴 偉，紀鎬南

(北京工業大學信息學部 北京 朝陽區 100124；計算智能與智能系統北京市重點實驗室 北京 朝陽區 100124)

參數估計是系統辨識中的一個重要內容，已有很多方法被提出。傳統的方法基于隨機誤差假設，如最小二乘法或極大似然法，它們假設誤差是統計特性已知的隨機變量。然而，當觀測數據不足或誤差是確定性時，采用隨機誤差假設不合適。

集員參數估計采用了更符合實際需要的誤差描述，即假定誤差是統計特性未知的有界變量。該方法的目的是給出所有與觀測數據、模型結構和誤差有界假設相一致的參數向量所組成的集合，稱這個集合為參數可行集。當參數為線性時，可行集為凸多面體。但是在很多實際應用場合，系統是參數非線性的，此時，可行集為非凸甚至非連通的。精確描述可行集十分困難，因此非線性系統集員參數估計的關鍵是找到一個既容易表達又能在計算成本與精度之間取得較好折中的可行集近似描述結果。

現有的非線性系統參數可行集近似描述方法可以粗略地分為以下4類：1)計算一個能包含可行集的集合，該集合稱為可行集的外界。外界可以是一個單一的凸集合，如盒子[1]、橢球[2]或多面體[3-4]，也可以是多個盒子的并集[5]。2)計算一個能包含于可行集的集合，該集合稱為可行集的內界。內界一般由可行集內的采樣點構成[2,6]。采用一個凸集合[1-4]作為可行集外界或在可行集內采樣[2,6]所得結果可能過于保守。3)用若干個盒子的并集[7-10]以任意精度從內外兩個方向逼近可行集的邊界，但是它的計算復雜度與參數的維數成指數關系。另外，復雜模型的最小包含函數很難構建，導致盒子過度保守使算法的收斂速度很慢。4)直接給出可行集的近似邊界[11-14]。這種方法可以處理針對復雜模型較難構建最小包含函數的問題。

本文給出一種新的非線性系統集員參數估計方法。該方法從流形學習的角度出發，視可行集邊界與n維空間中的單位球面(n-1-sphere)(n是參數的個數)為同胚，構造二者之間的同胚映射的近似。這個映射被建立后就可以用來將n-1-sphere映射為可行集近似邊界。構造該映射采用如下技術：首先，將等距映射(Isomap)[15]與數據歸一化結合，把在可行集邊界上均勻采樣得到的數據集映射為包含于n-1-sphere的數據集；然后，基于非參數方法得到可行集邊界與n-1-sphere的同胚映射的近似。本文方法的性能通過兩個例子加以說明。

1 問題的提出

定義非線性系統模型為：

式中，εk是已知正數。

集合PN稱為參數可行集。式(3)可改寫為：

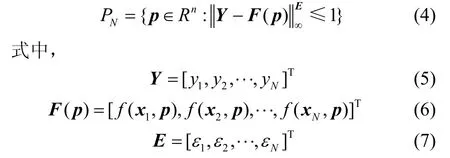
ek包含建模誤差和測量噪聲等，隨機方法假設誤差ek的統計特性已知或部分已知。但是該假設在實際應用中可能會出現問題，原因有：當觀測數據十分有限時，不易確定誤差ek的統計特性；在某些情況下誤差ek可能是確定性的。集員參數估計采用了更接近實際的有界誤差假設式(2)，該方法的目的是有效描述參數可行集PN。當系統是參數非線性時，可行集PN比較復雜，一般很難精確描述。近似描述可行集的方法有4種，已經在前面介紹。需要說明的是，這里假設可行集PN是有界且連通的。可行集是否連通涉及到可辨識性問題，該內容已超出本文的討論范圍，關于可辨識性請參考文獻[16]及其引用文獻。在假設可行集PN是有界且連通的前提下，下面給出一種逼近可行集邊界的方法。

2 基于Isomap的集員參數估計

2.1 可行集邊界的近似

圖1 映射(?)的構造

2.2 構造映射(?)的步驟1)和步驟2)

Isomap是一種概念上簡單但是很實用的流形學習方法，它可以將輸入數據映射到低維空間，并且在低維空間里數據的本征幾何屬性得到很好地保留。Isomap的優點在于較高的計算效率、較少的自由參數和非迭代全局優化。

1)通過先驗知識或者最優化方法得到一個包含可行集的盒子；

2)定義一個均勻的網格以覆蓋這個盒子；

3)用無導數線搜索方法找到可行集邊界與網格中盒子的邊的交點。

圖2 可行集邊界采樣

Isomap將數據對θi與θj之間的歐式距離d(i,j)作為輸入。用Isomap將數據集映射為數據集包含以下步驟：

1)構建鄰域圖G。當θi是θj的K個最鄰近點中的一個時，則將θi和θj相連，從而構成一個圖G，設定路徑的長度為d(i,j)。

2)計算最短路徑。若θi與θj相連，則初始化最短路徑否則，令，對，更新所有元素為更新過程完成之后，可以得到最短距離矩陣

3)計算嵌入。令λs是矩陣的第s個特征值(降序)，算子τ定義為其中矩陣L是距離的平方H是中心矩陣δij是Kroneckerδ函數。是第s個特征向量的第i個分量，然后令向量ρi的第s個分量為

運行Isomap所獲得的嵌入保持了流形的本征幾何屬性，但是它的形狀是不規則的。不難發現嵌入數據具有零均值和對角協方差。為了得到有規則形狀的數據集，需將數據集映射為數據集

2.3 構造映射(?)的步驟3)

2)通過最小化代價函數σ(w)=(約束條件為：且若ηi不是向量η的最近鄰，則wi= 0)計算最優線性重構權重wi；

2.4 近鄰個數K的確定

σ(K)越小，邊界近似效果越好。因此，最優近鄰個數K?應該是。最后，所構造的映射定為

3 數值仿真

3.1 例子1

考慮如下非線性系統模型[2]：

式中，yk和uk分別是系統輸出和輸入；p1和p2是參數。可以看出，回歸向量實驗過程中，設定并且設計輸入假設誤差ek在區間上服從均勻分布，因而，誤差界為1.5。實驗獲得數據集誤差序列?0.213 3,?0.586 1,?0.931 0,?0.919 7,0.546 7,?0.591 7,0.125 0,?1.047 4,0.593 7,?0.364 9,1.080 0,1.061 0,0.280 7,?0.010 3,1.199 3,0.964 9,0.434 7, 0.953 9,0.480 7,?0.474 1,?0.630 8,?0.476 4,0.102 2,0.681 3,?0.572 1,1.015 5,0.204 2,?0.388 8,0.608 2,0.139 7,?0.165 4,0.583 7,0.363 9,0.884 5,1.370 5,0.067 8,1.140 4,?0.981 1,1.439 2,?0.685 7,?0.743 0,1.127 2,0.711 9}。

圖3 可行集邊界采樣

借鑒文獻[1]的思想，采用最優化方法得到一個包含可行集的盒子，定義一個尺寸為41× 31的均勻網格以覆蓋這個盒子。計算可行集邊界與網格中盒子的與p2軸平行的邊的交點，共獲取76個。圖3顯示了這些可行集邊界采樣點，參數K′設定為2。在1-sphereS1上均勻取400個點代入式(9)和式(10)，以確定最優近鄰個數K。由于則設定K為28。圖4所示為σ與K的對應關系。圖5a和圖5b分別表示用本文方法和SVM方法[12]得到的可行集近似邊界。對于后者，使用了在上均勻采樣得到的130個點，及RBF核寬度為的LS-SVM來獲得最優結果。圖中實線和虛線分別表示精確邊界和近似邊界，加號表示參數向量的真值。從圖中可以看出，本文方法比SVM方法具有更好的逼近精度。同時也可以看出，用單一凸集合作為可行集外界的方法所得結果要比本文方法保守性高。

圖4 σ與K的對應關系

圖5 可行集近似邊界

3.2 例子2

考慮經典的單室開放一級吸收模型[11]：

式中，yk是在xk時刻觀察到的藥物濃度；Ka是吸收速率常數；Ke是消除速率常數；Dose是藥物劑量；V是分布容積。假設常數Ka和Ke是待估計量，實驗過程中，設定V=60 L。口服藥物1 100 mg后，分別在0.25、0.5、1、1.5、2、4、6、8、10、12、18、24 h后測量血漿中的藥物濃度，從而獲得一個輸入輸出數據集。假設誤差ek服從均值為0 mg/L和標準差為0.25/3 mg/L的截斷正態分布，誤差序列?0.004 9,?0.084 2,0.051 2,0.042 3,0.141 0,0.049 3,?0.053 6,0.031 7,?0.084 1,?0.001 6,?0.004 0}。因而，誤差界為0.25 mg/L。

圖6 可行集邊界采樣

圖7 σ與K的對應關系

借鑒文獻[1]的思想，采用最優化方法得到一個包含可行集的盒子[1.54,1.66]×[0.355,0.395]。定義一個尺寸為31× 21的均勻網格以覆蓋這個盒子。計算可行集邊界與網格中盒子的邊的交點，共獲取84個。圖6顯示了這些可行集邊界采樣點。參數K′設定為6。在上均勻取400個點代入式(9)和式(10)，以確定最優近鄰個數K。由于，則設定K為25。圖7示出了σ與K的對應關系。圖8a和8b分別為用本文方法和SVM方法[12]得到的可行集近似邊界。對于后者，使用了在[1.54,1.66]×[0.355,0.395]上均勻采樣得到的147個點，及RBF核寬度為的LS-SVM來獲得最優結果。圖中實線和虛線分別表示精確邊界和近似邊界，加號表示參數向量的真值。從圖中可以看出，本文方法比SVM方法具有更好的逼近精度。

圖8 可行集近似邊界

4 結束語

本文給出一種新的非線性系統集員參數估計方法，可以處理針對復雜模型較難構建最小包含函數的問題。該方法假設可行集是有界且連通的，尋找可行集邊界與n-1-sphere之間同胚映射的近似。映射構造成功后，就可以將n-1-sphere映射為可行集的近似邊界。本文通過兩個例子說明該方法的優勢。接下來的工作將研究如何將方法延伸到用于有界非連通可行集的邊界逼近。

[1]MILANESE M, VICINO A.Estimation theory for nonlinear models and set membership uncertainty[J].Automatica,1991, 27(2): 403-408.

[2]BAI E W, ISHII H, TEMPO R.A Markov chain Monte Carlo approach to nonlinear parametric system identification[J].IEEE Transactions on Automatic Control,2015, 60(9): 2542-2546.

[3]CHAI W, SUN X F, QIAO J F.Set membership state estimation with improved zonotopic description of feasible solution set[J].International Journal of Robust and Nonlinear Control, 2013, 23(14): 1642-1654.

[4]BRAVO J M, ALAMO T, REDONDO M J, et al.An algorithm for bounded-error identification of nonlinear systems based on DC functions[J].Automatica, 2008, 44(2):437-444.

[5]BORCHERS S, FREUND S, RATH A, et al.Identification of growth phases and influencing factors in cultivations with AGE1.HN cells using set-based methods[J].PLoS ONE,2013, 8(8): e68124.

[6]NURULHUDA K, STRUIK P C, KEESMAN K J.Set-membership estimation from poor quality data sets:Modelling ammonia volatilisation in flooded rice systems[J].Environmental Modelling & Software, 2017, 88: 138-150.

[7]JAULIN L, WALTER E.Set inversion via interval analysis for nonlinear bounded-error estimation[J].Automatica, 1993,29(4): 1053-1064.

[8]RA?SSI T, RAMDANI N, CANDAU Y.Set membership state and parameter estimation for systems described by nonlinear differential equations[J].Automatica, 2004, 40(10):1771-1777.

[9]HERRERO P, DELAUNAY B, JAULIN L, et al.Robust set-membership parameter estimation of the glucose minimal model[J].International Journal of Adaptive Control and Signal Processing, 2016, 30(2): 173-185.

[10]PAULEN R, VILLANUEVA M E, CHACHUAT B.Guaranteed parameter estimation of non-linear dynamic systems using high-order bounding techniques with domain and CPU-time reduction strategies[J].IMA Journal of Mathematical Control and Information, 2016, 33(3):563-587.

[11]LAHANIER H, WALTER E, GOMENI R.OMNE: a new robust membership-set estimator for the parameters of nonlinear models[J].Journal of Pharmacokinetics and Biopharmaceutics, 1987, 15(2): 203-219.

[12]KEESMAN K J, STAPPERS R.Nonlinear set-membership estimation: a support vector machine approach[J].Journal of Inverse and Ill-Posed Problems, 2004, 12(1): 27-41.

[13]HERRERO J M, BLASCO X, MARTINEZ M, et al.Non-linear robust identification using evolutionary algorithms: Application to a biomedical process[J].Engineering Applications of Artificial Intelligence, 2008,21(8): 1397-1480.

[14]CHAI W, SUN X F.Set membership estimation by weighted least squares support vector machines[J].Electric Machines and Control, 2009, 13(3): 431-435.

[15]TENENBAUM J B, de SILVA V, LANGFORD J C.A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000, 290(5500): 2319-2323.

[16]JAUBERTHIE C, TRAVE-MASSUYES L, VERDIERE N.Set-membership identifiability of nonlinear models and related parameter estimation properties[J].International Journal of Applied Mathematics and Computer Science,2016, 26(4): 803-813.

[17]LEE J A, VERLEYSEN M.Nonlinear dimensionality reduction of data manifolds with essential loops[J].Neurocomputing, 2005, 67: 29-53.

[18]CHAI W.Nonlinear set membership identification by locally linear embedding[J].International Journal of Innovative Computing, Information and Control, 2014,10(6): 2193-2207.

[19]SAUL L K, ROWEIS S T.Think globally, fit locally:Unsupervised learning of low dimensional manifolds[J].Journal of Machine Learning Research, 2003, 4(2):119-155.