基于磁致旋光效應測量有限長通電螺線管軸向磁場分布
莊浩麗,韓俊彥,林佳佳,李苑喆,張舒婷,曾育鋒
(華南師范大學 物理與電信工程學院,廣東 廣州 510006)
目前,研究有限長通電螺線管空間軸向磁感應強度分布通常基于霍爾效應,用特斯拉計或半導體磁敏元件等間隔伸入通電螺線管內部測量各位置的磁感應強度. 霍爾效應的產生需要在垂直于外磁場的方向上通以電流,電流的磁效應會使霍爾元件的附近形成磁場,與通電螺線管內部的磁場疊加,由此會給測量結果帶來誤差. 考慮到倍頻法研究法拉第磁致旋光效應[1]的精度較高,而且基于光學原理的測量方法不會在通電螺線管內部產生附加磁場,所以筆者嘗試用法拉第磁致旋光效應探究有限長通電螺線管空間軸向磁感應強度分布.
1 理論分析
1.1 有限長通電螺線管空間磁場分布
設有限長通電螺線管的長度為L,半徑為R,單位長度的匝數為n,電流為I,有限長通電螺線管如圖1放置,由于螺線管具有對稱性,只研究取yOz平面的磁場分布,y和z分量分別是徑向和軸向分量. 根據磁場強度矢量與磁矢勢的微積分關系,求出空間點的磁場,然后再通過橢圓積分,利用Mathematica數學軟件從理論上畫出了通電螺線管軸向空間點磁感應強度的分布,如圖2所示[2].

圖1 螺線管示意圖
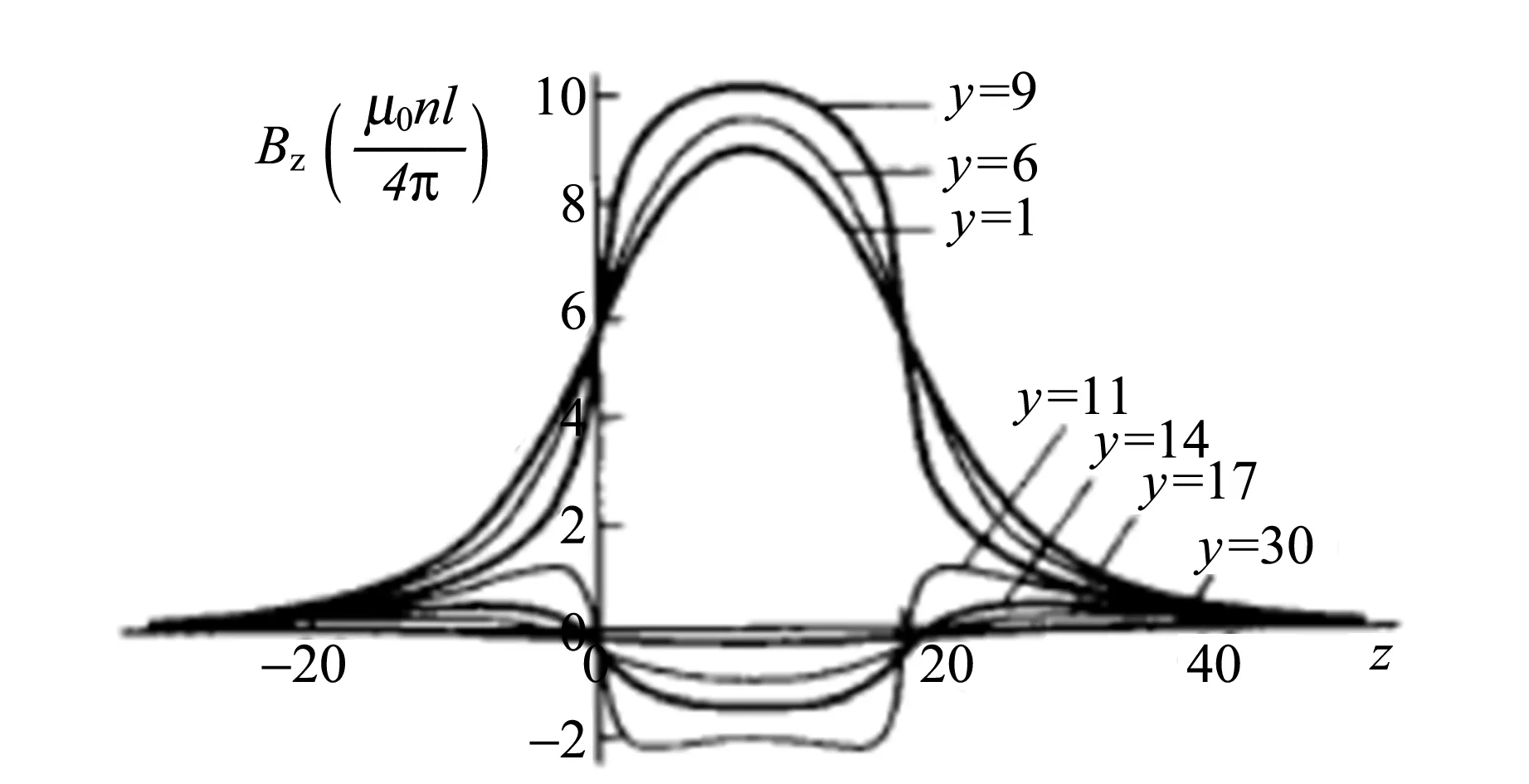
圖2 固定y,軸向分量Bz與z的關系
1.2 法拉第效應
法拉第磁光效應是指:線偏振光通過放置在磁場中的磁光玻璃,沿著磁場方向傳播時,光的偏振面發生偏轉[3].
已知對于順磁介質和抗磁介質,磁場不是很強時,偏振面的旋轉角θ與光在介質中通過的路程L、外加磁感應強度B在光傳播的方向上的分量成正比
θ=VBL,
(1)
比例系數V由物質和工作波長決定,表征物質的磁光特性,稱為費爾德常量,對于順磁介質和抗磁介質,V為常量.
而對于有限長的通電螺線管的軸向磁場分布存在分布不均勻的情況,所以磁致旋光效應是介質長度內的積分效果,即
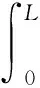
(2)
其中B(z)可根據文獻[2],令y0=0,即可得到有限長通電螺線管z軸的軸向磁場分布為
(3)
1.3 倍頻法
在法拉第磁光效應實驗中發現,晶體在調制勵磁線圈正弦交變磁場的作用下產生交變的振動面旋轉,當起偏器與檢偏器振動方向平行或者正交時,可從示波器觀察到頻率為調制信號2倍的倍頻信號,這就是磁光調制的倍頻現象[4]. 通過數學推導和實驗分析可以證明當偏振夾角為0和π/2時會發生倍頻現象.
實驗利用法拉第效應實驗儀、雙蹤示波器,分別在樣品不外加磁場以及加入磁場下,讀出出現倍頻現象時測角儀的度數,2次讀數的差值為交流磁場B所引起的法拉第旋轉角.
2 實驗系統及測量結果
實驗測量光路如圖3所示,樣品在通電螺線管內移動的示意圖如圖4所示. 實驗中,選取介質長度為10.0 cm的重火石玻璃樣品. 向右為正方向建立一維坐標,設坐標0剛好是螺線管左邊界的起始點,以樣品的左邊界為參考點.在磁場恒定的情況下,每移動1 cm,記錄1次樣品的偏轉角,直至樣品完全移到螺線管外,得出樣品在不同位置時偏振光經過樣品后的偏轉角隨相對位置變化的關系曲線,改變磁場強度,重復實驗. 本實驗通過改變通電螺線管的電流來改變磁場強度,如圖5所示.
再次測量樣品完全在通電螺線管內移動時的數據,得到樣品在相對位置在0~10 cm處時偏振光的磁致旋光偏轉角隨相對位置的變化關系圖(如圖6所示). 由圖6可以看出在有限長通電螺線管的內部,軸向磁場先增大后減小,在螺線管中間最強,兩邊稍弱,但仍可近似看作均勻磁場,符合文獻[2]中數值計算的結果,如圖2所示.
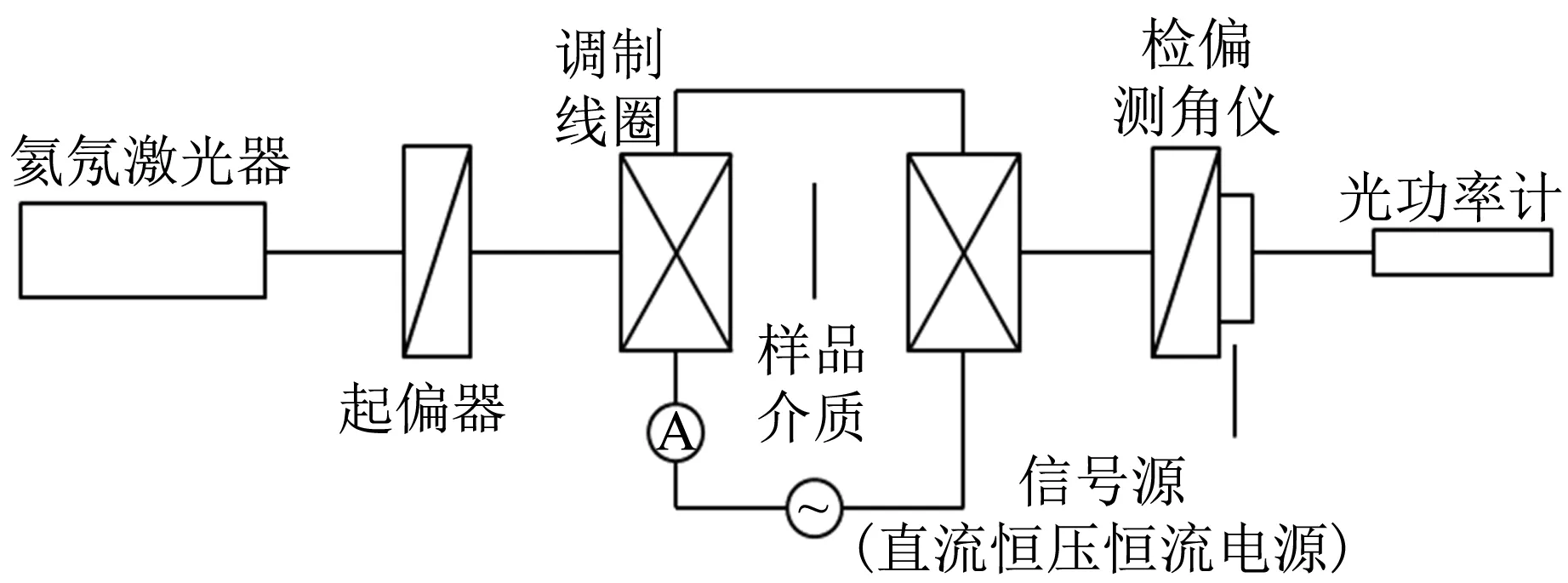
圖3 測量光路圖
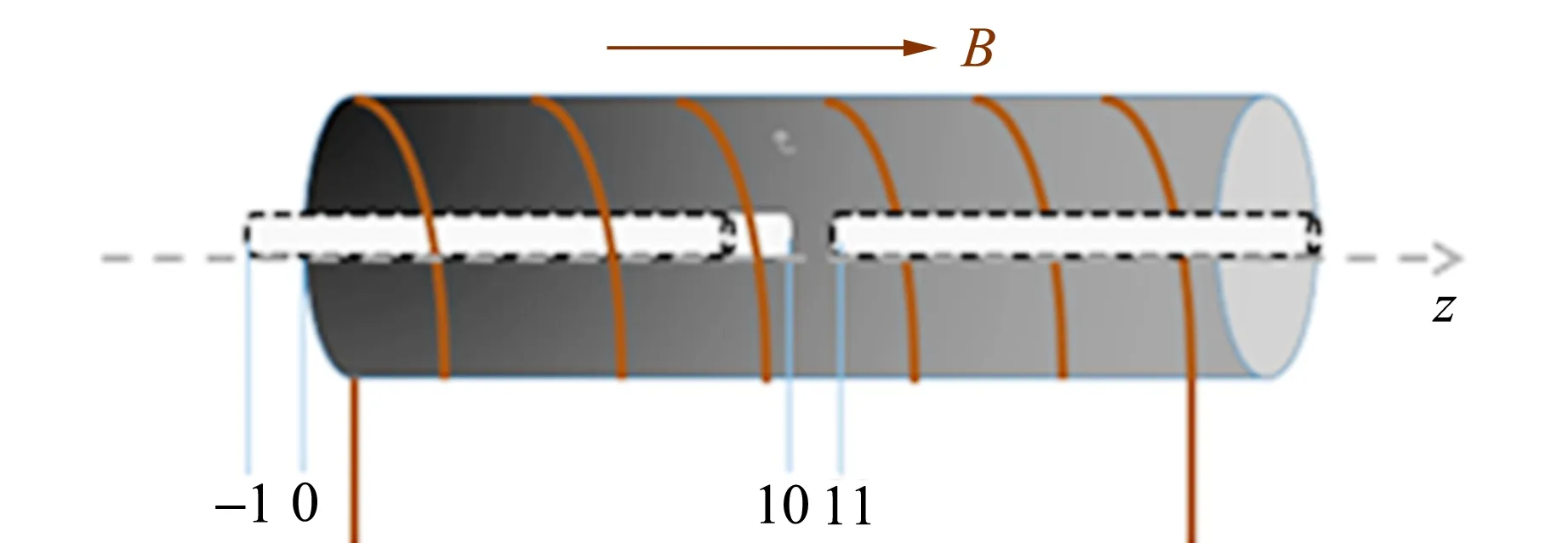
圖4 樣品在通電螺線管內移動示意圖
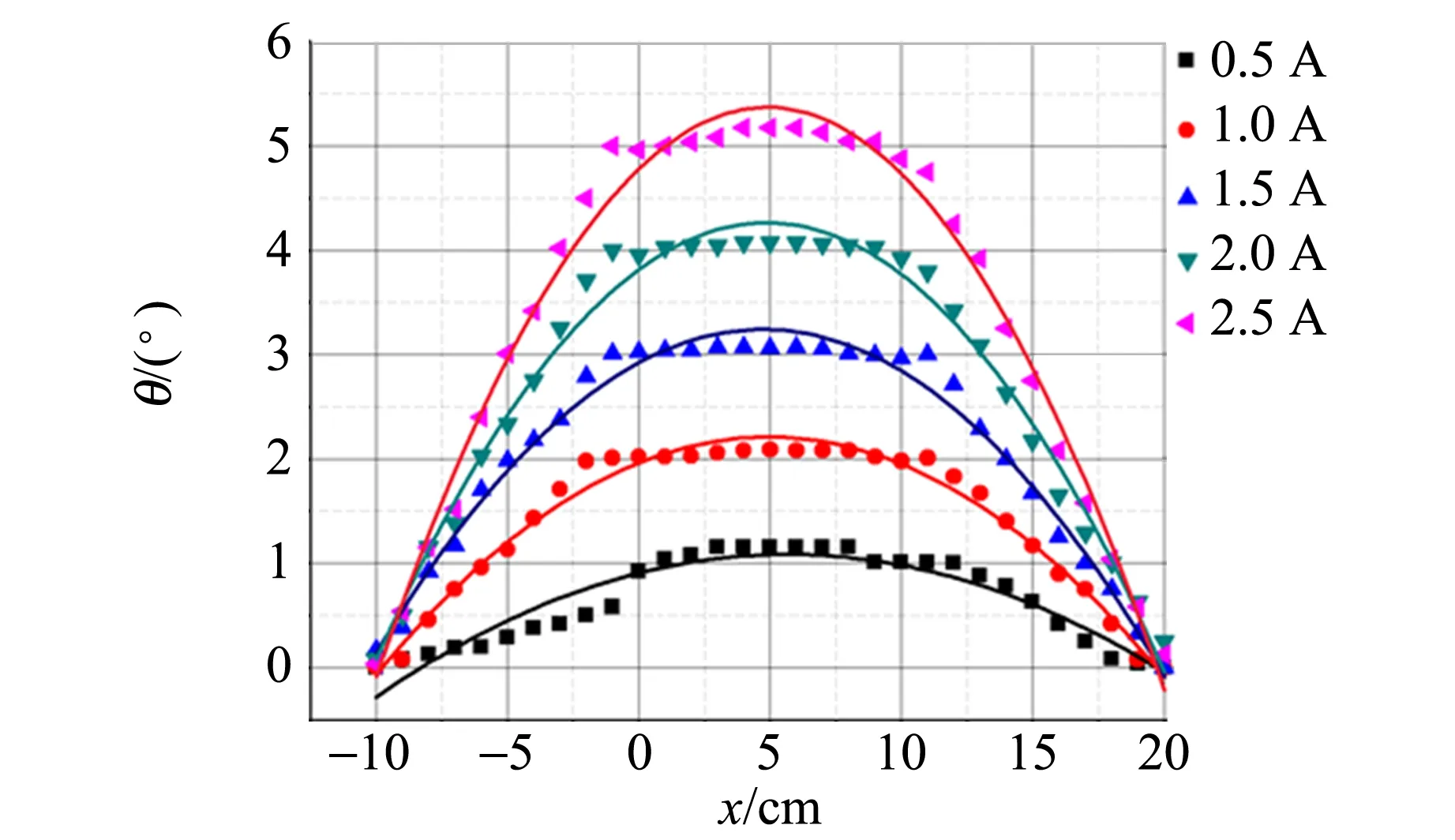
圖5 不同電流下磁致旋光偏轉角隨相對位置的變化關系圖
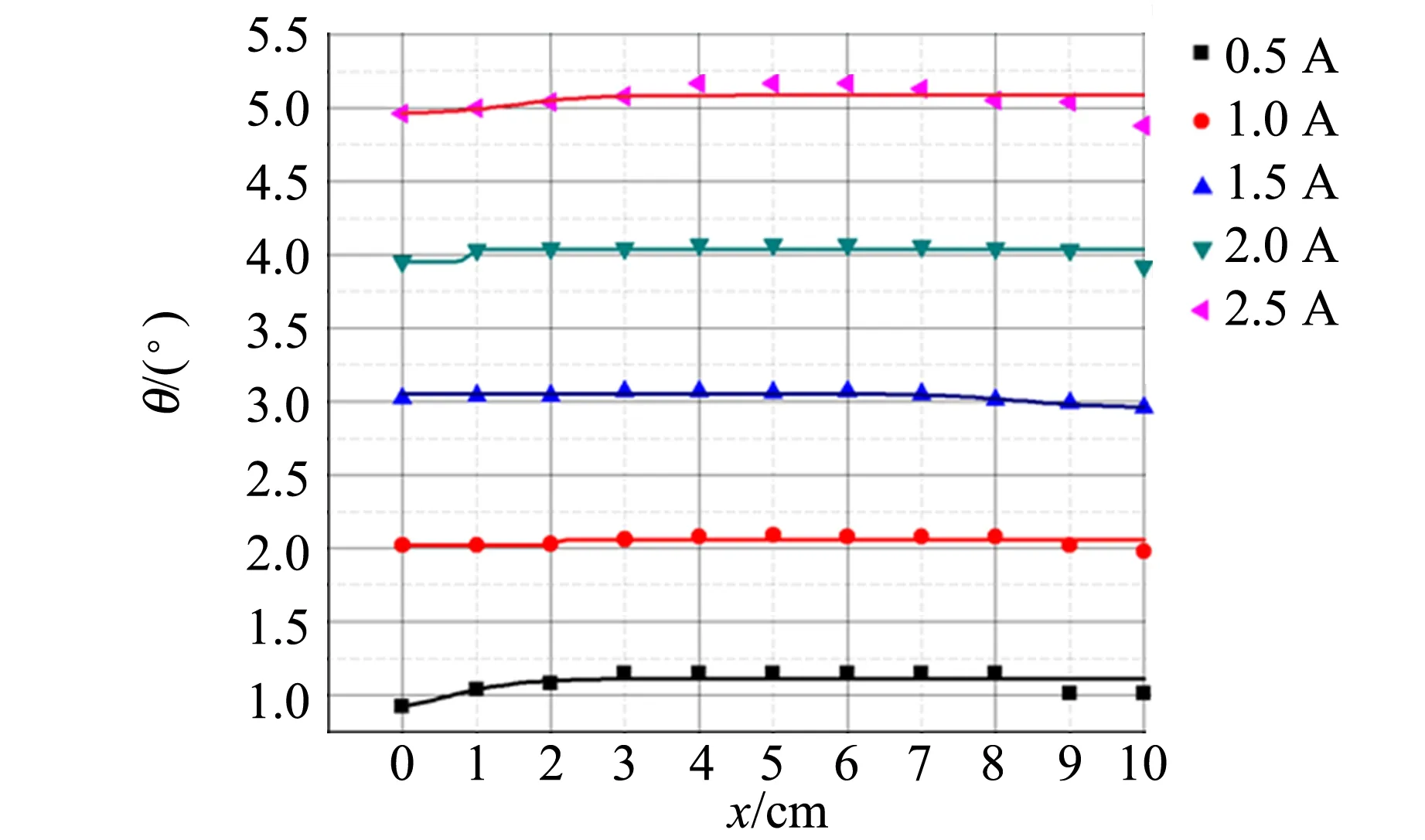
圖6 不同電流下磁致旋光偏轉角隨相對位置的變化關系圖
由于通電螺線管兩端的軸向磁感應強度分布是對稱的,故只分析一側數據. 提取圖像中的后11個點來研究在有限長通電螺線管外的軸向磁感應強度的分布.若通電螺線管外部不存在磁場,所有的點都應落在曲線第1個點與點(0,20)相連的直線上或均勻分布在直線兩側,但實際上所有點幾乎都會落在直線的上方(圖7),說明在螺線管外的介質仍然受到了軸向磁場的作用.設在螺線管內的介質的長度為L′,由于外部微弱磁場的作用,使有效長度L略微大于L′,根據θ=VBL,θ會略微偏大,則證明通電螺線管外部仍有軸向磁感應強度分布,但相對于螺線管內部的磁感應強度小得多,同樣符合圖2的數值模擬結果.偏轉角θ與樣品的相對位置不嚴格成線性是螺線管內部與外部的磁場與介質有效長度共同影響的結果.
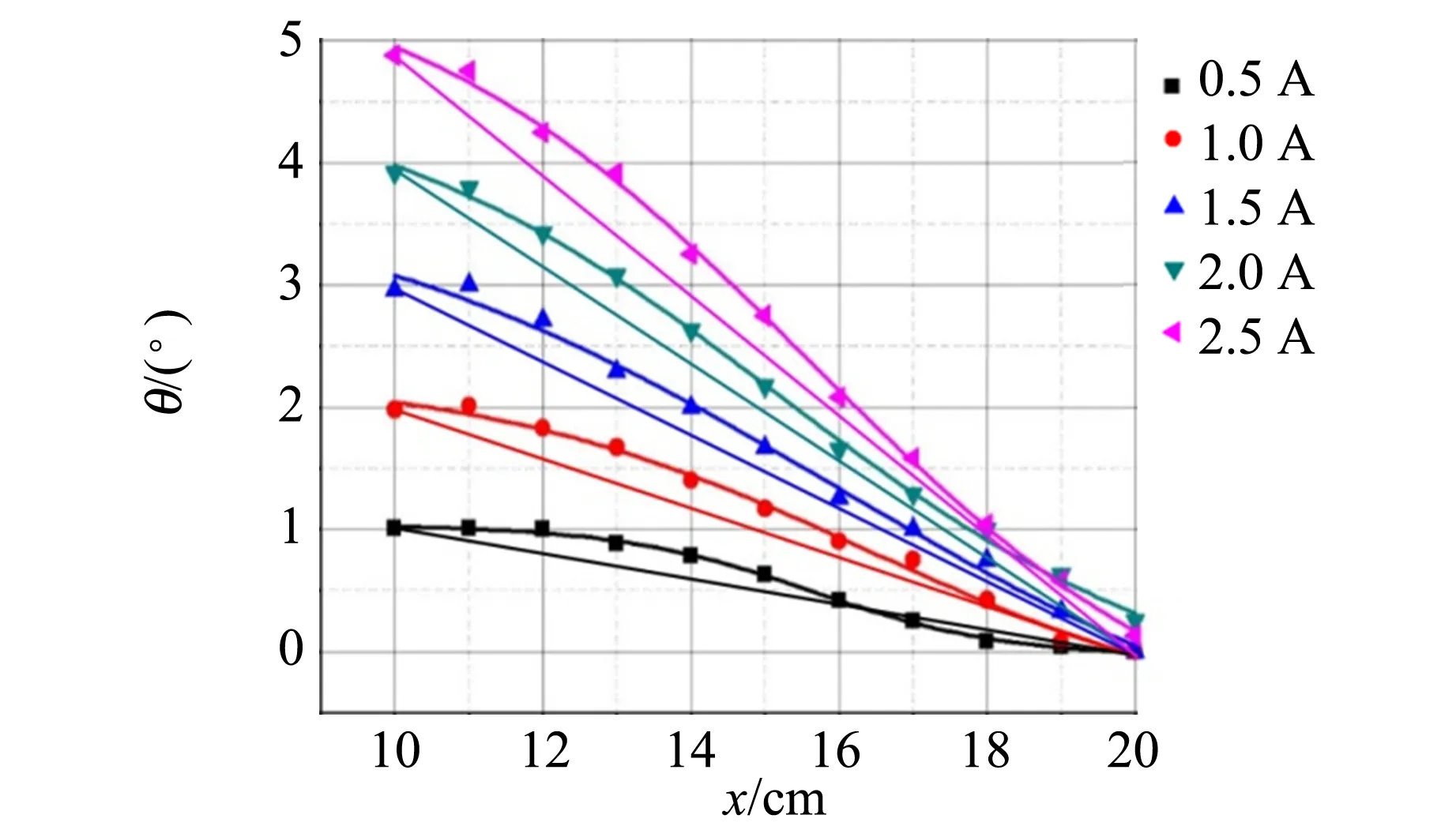
圖7 樣品在螺線管10~20 cm處時偏振光的磁致旋光偏轉角隨相對位置的變化關系圖
3 結束語
基于磁致旋光效應原理,探究驗證有限長通電螺線管空間軸向磁場分布的情況. 經對圖像的分析可知,有限長通電螺線管內部的軸向磁場近似是勻強磁場,但兩端磁感應強度會略微減弱;通電螺線管外部仍然有軸向磁場分布,但是磁感應強度隨離螺線管距離的增大而快速減小.
[1] 吳思誠,王祖銓. 近代物理實驗[M]. 北京:北京大學出版社,1995.
[2] 惠小強,陳文學. 有限長通電螺線管空間的磁場分布[J]. 物理與工程,2004,14(2):22-23,25.
[3] 鐘錫華. 現代光學基礎[M]. 北京:北京大學出版社,2012.
[4] 陸遙,陳銘南,倪晨. 法拉第效應實驗中倍頻現象的研究[J]. 大學物理,2010,29(4):60-62.
[5] 底楠,徐曉鵬. 關于磁光調制倍頻法的討論和改進[J]. 物理實驗,2007,27(5):10-12,16.
[6] 劉公強,劉湘林. 磁光調制和法拉第旋轉測量[J]. 光學學報,1984,4(7):588-592.
[7] 孟甜甜,符照森,劉輝,等. 基于磁光調制原理的高精度偏振角測量方法模擬與實驗研究[J]. 西北大學學報(自然科學版),2011,4(6):965-968.
[8] 侯昭武. 通電螺線管空間點的磁場[J]. 廣西民族學院學報(自然科學版),2005,11(1):105-108.
[9] 羅浩,向澤英,謝英英,等. 霍爾效應法測磁場實驗誤差研究[J]. 大學物理實驗,2015,28(4):99-102.
[10] 渠珊珊,何志偉. 基于霍爾效應的磁場測量方法的研究[J]. 電測與儀表,2013,50(10):98-101.
[11] 蔡偉,伍樊成,楊志勇,等. 磁光調制技術與應用研究[J]. 激光與光電子學進展,2015,52(6):24-33.
[12] 孫可芊,李智,廖慧敏,等. 霍爾效應中副效應的研究[J]. 物理實驗,2016,36(11):36-40.

