中學數學的目標單元教學設計

高媛

傳統的單元教學設計，知識的傳授非常清晰，單元與單元之間的邊界看上去也非常清晰，但教師的注意力往往集中在知識上，忽略思維方法和情感態度價值觀的培養。因此，在一個知識單元中，很難甚至不可能完成對學生的某種思維方法或某種態度的培養。本文所講的單元，是實現教學目標的相對完整的過程，是教學過程的質的基本單位，也是衡量教師教學和教材駕馭能力的基本單位，是課程螺旋式上升的基本單位，也是課程設計的基本單位。

在近兩年的研究中，我們所設計的單元存在著不斷擴大的三個層次：一節課內的調整；章節內的重組；跨越章的整合。針對每一個層次，我們都進行了教學實踐，并摸索出了一些在該層次內進行目標單元教學設計的方法。

一、課內的調整

以“不等式的基本性質”一課為例。這節課原本的設計思路是：先復習等式性質，然后請學生類比及猜想不等式的性質，進而借助數驗證關于不等式性質的猜想，得出性質，再利用不等式的性質解一些簡單的不等式。經思考與重新設計，我們讓學生先自己嘗試去解不等式，然后說出自己為什么會認為用這樣的步驟可以解不等式。這其實是引導學生覺察到自己是在類比解方程的步驟、等式的性質。其間，不要關注學生解的結果對錯，而要關注解的過程。

在教學實踐中，學生果然能夠直接解簡單的不等式，而通過對解集對錯的分析，最終自然地將問題集中到算理上，即對不等式性質的探討。其中，和等式性質類似的幾條自然不會有異議，矛盾最集中的就是“不等式兩邊同時乘或除以一個負數時，不等號的方向是否改變”這一問題。學生在解釋自己的做法正確時用了多種思路，如枚舉、利用數軸數形結合地去看、分類討論甚至用字母證明。這種充分的論證過程，讓學生印象更加深刻，難點的突破顯得很自然，證明中思想方法的使用更是超出教師預料。

這種設計最大的調整，是把教學過程“倒過來”，也就是將傳統的先講不等式的性質、再解不等式的教學順序，調整為先解不等式，再從中梳理出不等式的性質。而這種調整的本質，是以學生研究問題、解決問題以及對解決問題過程的反思作為教學的基本線索。期間，教師對學生進行研究，根據學生的表現組織教學，這種教學模型叫做“基于學生研究的數學教學”模型（見圖1）。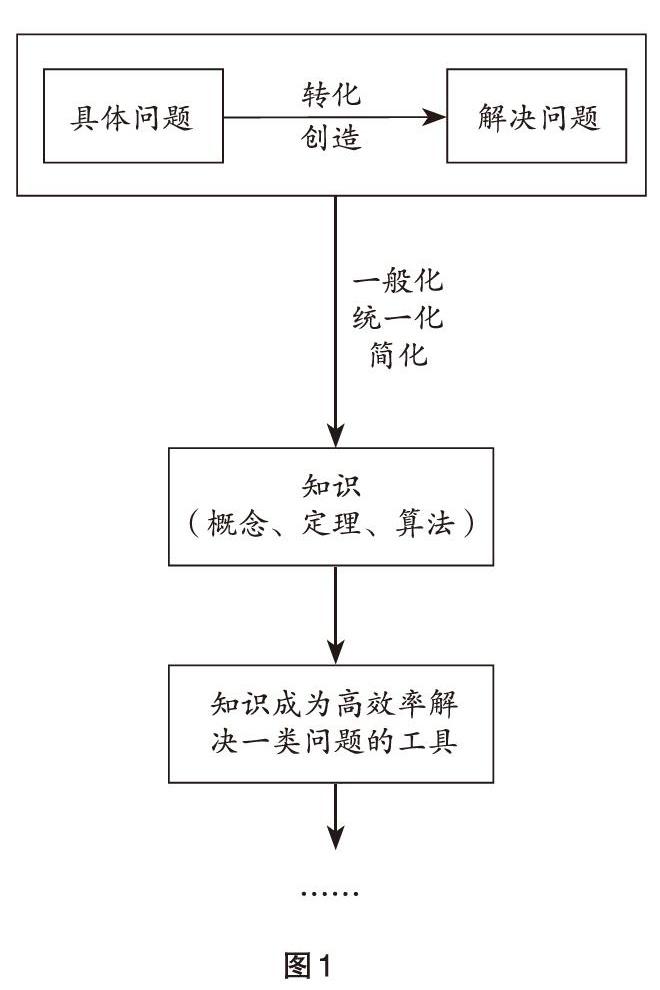

在“基于學生研究的數學教學”模型中，知識產生過程的教學部分包括兩個階段。

第一階段為解決具體問題階段，即“做數學”。“做數學”就是學生憑借自己已有的基礎解決數學問題，如解簡單不等式、解決一個實際問題等。這一階段需要放手讓學生去做，不規定方法，而是讓學生充分展示自己面對問題時的各種想法，包括困難。

第二階段為反思階段，也就是讓學生對“做數學”的過程進行分析。例如，解不等式的過程運用了哪些步驟，是怎么想到這些步驟的，覺得每個步驟可靠嗎，為什么，是否有其他的方法等。反思階段就是讓學生對解決問題過程中的智慧或者困難進行展示，師生共同將“做數學”活動中獲得的經驗和教訓作為素材進行分析，找到通性通法，概括為知識。

基于學生研究的教學模型重視“問題解決”在數學學習中的作用，力求為學生設計具有吸引力、挑戰性的問題，為學生提供通過自主解決問題從而帶來更多思想方法的可能。由于解決問題的過程會涉及更多的知識，特別是有可能會用到傳統的教學計劃中日后才要求掌握的知識，這就要求教師調整自己的教學設計單位，除了課時內的調整，還需要將章節內容進行重組，或者實施跨章節的整合。

二、章節內容的重組

在“二次函數”單元的起始課，我們選擇的是非常常見的一道實際問題：如圖2，用24米的籬笆靠墻（限寬10米）圍矩形菜地，中間用籬笆截成左、右兩部分，問所圍菜地的最大面積為多少平方米？

不同的是，以往這一問題是單元知識學習完后，在二次函數的應用一節中出示，因為這個問題的解決幾乎用到二次函數的全部重要知識：配方法求最值，且最大值在頂點處不能取到的情況，學生容易不考慮x的取值范圍而出錯，直接回答最值為48m2。但是我們在出示這個問題后，放手讓學生去解決。

學生果然有行動、有想法，他們的方法很樸素，也出現了意料之中的錯誤。方法1：選擇枚舉求解二元不定方程，發現取值具有對稱性，得到48m2。方法2：通過列代數式，利用配方法也求得48m2。在驗證答案時，有人想到了10m限寬，如果x=4m，則不能圍出菜地。

那么，到底菜地最大的面積是多少？用什么方法去求呢？通過對寫在黑板上的x與S間的對應關系，學生逐漸意識到，自己正面對一個新的函數問題。而函數問題關注的是S隨著x在符合要求內的變化而變化的關系，因此，首先要確定x的變化范圍，然后可以借助表格、圖像等方式刻畫變化關系，通過分析，得到了x最小取值為14/3，最大為140/3。通過分析數表、圖像和配方后的解析式，看到在x的取值范圍內，S隨著x取值變大，于是，確定當x=14/3時，面積達到最大140/3m2。

在對這個問題的解決過程的反思中，拋去具體情境，聚焦到這里出現的新函數的特征，根據解析式特征命名為二次函數，分析二次函數的定義以及定義帶來的定義域的特點，從列表中，發現表格數據的對稱性，畫出圖像后，同樣驗證了其對稱性的特點，并發現圖像有最高點，函數存在最值，進而提出：是不是所有的二次函數的數值和圖像都有這種特征？為后面系統、細致的研究播下了問題的種子。

從解決體現知識價值的實際問題入手，由于問題的解決可能需要較多的知識，甚至可能需要用到按照原有教學計劃還未曾學習的知識，這就需要擴大教學設計單位?！岸魏瘮怠眴卧褪且粋€典型。這一單元的起始課中的實際問題的解決，實際上用到了這章的許多重點、難點知識，然而，考慮到學生一次函數、一元二次方程的學習基礎，學生是可以面對這樣的問題的。

在章節內以問題解決為線索開展教學，帶來的是教學內容的整合，教給學生的是知識結構而不是一個個的知識點。這樣，知識的學習過程就會具有遷移性，而一些深層次問題的思考、提出與解決，則進一步要求跨越章、跨越年級的知識整合。

三、跨越章的整合

以“包裝盒的設計”一課為例，從具體知識的角度看，主要是“正方體的展開圖”，而一般的教學也都是以“正方體的展開圖”作為課題名稱，教學的過程則是為學生提供正方體盒子，請學生剪開、展平，得到各種形狀的展開圖，再通過幾何畫板進行演示、補充，得到所有的展開圖，教給學生記憶的方法，然后進行辨析練習。其中，用于教學的正方體盒子，經常是教師提前根據圖紙糊出來的。

我們則采用了一種新的設計思路：請學生設計圖紙，使之能夠折成一個正方體。這樣的設計思路，背后是我們如下幾點考慮。

第一，揭示知識的實用價值。知識的價值在于解決問題，特別是解決現實問題。在現實中，正方體的展開圖并非用于剪開正方體盒子并將其展平，而是為了得到正方體的包裝盒的設計圖紙，因此，本節課先向學生展示一個精美包裝盒，提出“這個包裝盒是怎樣得到的”這一問題，經分析學生認識到其中的關鍵是圖紙，接下來明確學生需要解決的問題：還原設計師的設計過程，設計一個可以折成正方體的圖紙。

第二，展開初中幾何核心問題與概念的全景圖。一個班40名學生至少能設計出40張圖紙，但這些設計圖有很多是相同的，那么，在什么情況下是相同的？這就涉及幾何中的全等、相似概念，而判斷全等、相似的方法，則涉及旋轉、軸對稱、平移等概念，所以，通過“我們到底設計出了多少個方案”的問題的探討，學生思維深處的這些概念被激活，關于幾何研究的主要問題的全景圖也在教師的引導下被打開。

第三，體會研究幾何問題的基本方法。40名學生未必能夠產生全部的正方體的展開圖，而在將重復的方案拿出后，對余下的方案進行認識的最基本的步驟就是分類。通過分類，這些方案變得有了一定的關系、秩序和規律，新的問題也自然涌現：是否我們找全了所有的設計方案？為了解決這個問題，需要借助分類后的方案系統思考每種類型是否還有其他可能。從簡到繁，逐步走向完善。期間，又必須借助分析推理、空間想象、實驗操作等方法。

這樣，“正方體的展開圖”這一并非很重要的具體知識就成為了讓學生整體認識幾何研究的對象、問題、方法的載體，在初中“圖形與幾何”領域中的其他諸如三角形、四邊形、圓等對象的學習中，這些問題與方法將被反復應用。學生在積累越來越多的幾何具體知識的同時，也會不斷深化對“幾何到底研究什么問題、應用什么研究方法”的認識與理解。

（作者單位：北京市第十三中學分校；指導教師：北京教育學院頓繼安）

責任編輯：肖佳曉