星載串聯型柔性抓捕機構的多級阻尼鎮定控制
褚 明, 董正宏, 任珊珊, 賈慶軒(1. 北京郵電大學 自動化學院,北京 100876; 2. 空間機器人技術教育部工程研究中心,北京 100876; . 航天工程大學 科研學術處,北京 101416)
在軌捕獲是開展在軌維修、裝配及碎片清除等空間任務的重要環節。利用星載抓捕機構與目標航天器對接時,瞬時碰撞力產生的脈沖式動量易引起漂浮基座的姿態傾斜和角動量超限,且抓捕機構的傳動關節處會產生沖擊振動,該類動力學響應使得捕獲后的系統產生擾動,嚴重時可導致失穩。因此,最大程度地減小碰撞動量對漂浮基座的擾動,且快速衰減抓捕機構傳動關節處的振動,成為在軌捕獲的關鍵技術之一。近年來,利用串聯型多自由度機械臂開展在軌捕獲成為該領域的熱點課題,國內外諸多學者研究了通過星載機械臂完成在軌捕獲過程的動力學分析和鎮定控制方法。Xu等[1]討論了柔性冗余機械臂的運動學冗余特性,通過機械臂的預構型方法緩解在軌捕獲引起的振動和沖擊。叢佩超等[2]提出直臂抓取的概念,基于機械臂動量守恒提出碰撞前的配置規劃方法,以減小耦合角動量并實現穩定捕獲。Wei等[3]提出一種動態抓取域方法來減小振動沖擊,從而消除碰撞沖量對漂浮基座的擾動影響。Liu等[4]對捕獲后的柔性機械臂進行動力學建模,采用PD控制器實現捕獲碰撞后系統的快速穩定。Dong等[5-6]針對雙關節漂浮基柔性空間機械臂在軌捕獲衛星過程的接觸、碰撞動力學建模和碰撞后混合體系統鎮定運動控制及柔性振動主動抑制問題進行了研究。利用阻尼力實現柔性機構的振動抑制是主動控制的重要方法之一[7-9],磁流變阻尼器[10]具有阻尼力可控和響應快速的特征,在振動控制領域應用廣泛。Nguyen等[11]將阻尼可控的磁流變阻尼器用于空間捕獲的平面二自由度機械臂模型,定性驗證了帶有反饋比例控制器的阻尼器可以有效抑制旋轉目標的角動量,減小碰撞對系統的影響,但其成果僅局限于少自由度模型和阻尼力的開關控制,未解決多自由度模型下多級可控阻尼的優化控制問題。
本文基于十字軸結構的軟接觸關節裝置[12],提出一種具有多級可控阻尼的串聯型柔性抓捕機構廣義模型,通過在關節處引入多維可控阻尼器,再由多個關節和連桿組成多自由度串聯機構,能實現對空間任意方向碰撞動量的緩沖和卸載。采用Kane方法建立漂浮基座耦合柔性抓捕機構的一體化動力學方程,利用微粒群尋優算法實現多級最優阻尼力的求解,實現了捕獲后不穩定系統的鎮定控制。最后,對提出的鎮定控制方法進行數值仿真和性能對比,結果表明,微粒群優化控制方法能有效消除碰撞力對漂浮基座的擾動,保證基座姿態穩定的同時抑制了柔性抓捕機構的振動。
1 具有多級阻尼的柔性抓捕機構模型
提出一種具有多級可控阻尼的N(N為自然數)關節柔性抓捕機構模型,如圖1所示。Oxyz為慣性坐標系,Oixiyizi(i=1,2,3,…,N+1)順次為漂浮基座和剛性連桿端面處的連體坐標系,在每個連桿的端面連體坐標系處為連接各個連桿的關節。關節處設置可控阻尼器件,以第j個端面連體坐標系為例(j=2,3,…),分別沿Ojxj、Ojyj、Ojzj三個坐標軸的直線方向設置三個直線阻尼器,用于鎮定沿該三個坐標軸直線方向的碰撞動量;分別繞Oixi、Oiyi、Oizi三個坐標軸旋轉方向設置三個旋轉阻尼器,用于鎮定繞該三個坐標軸旋轉方向的碰撞動量,故每個關節均可對空間六維方向的碰撞動量實現鎮定。通過N個連桿將關節進行串聯,可組成具有6N自由度的多級阻尼柔性抓捕機構。

圖1 具有多級阻尼的串聯型柔性抓捕機構模型
2 動力學方程
由于阻尼器具有一定的剛度系數和阻尼系數,因此,每個關節可簡化為6個彈簧模型和6個阻尼模型,則N關節柔性抓捕機構可離散為由6N個彈簧和6N個阻尼連接的多剛體段模型。若將漂浮基座視為具有6個自由度的虛擬連桿,則帶有漂浮基座的N關節柔性抓捕機構可等效為具有(6N+6)個自由度的固定基座系統。采用Kane方法對帶有漂浮基座的N關節柔性抓捕機構進行一體化動力學建模,可得到柔性抓捕機構捕獲后動力系統的廣義微分方程。
2.1 變換矩陣
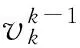
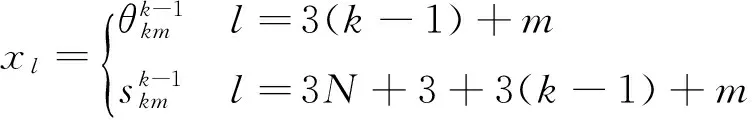
(1)

(2)
Okxkykzk相對于慣性系Oxyz的絕對變換矩陣
(3)
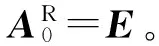
則任意剛體段的運動學方程
(4)
式中:c=cos,s=sin。
2.2 偏角速度和偏線速度
慣性坐標系中,第k段的角速度
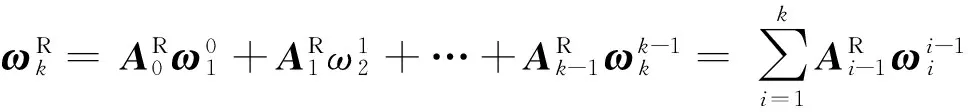
(5)
則偏角速度
(6)
用矩陣Wkl存儲剛體k對廣義速度yl的偏角速度
(7)
式中:l=1, 2, 3, …, 6N+6。
剛體k的質心在慣性系下的位置矢量
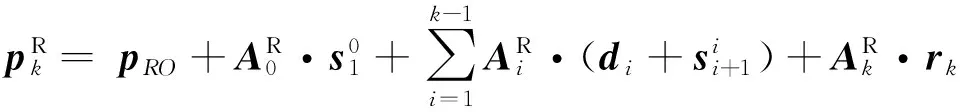
(8)
式中:pRO為坐標系O1x1y1z1在慣性系中的位置矢量;di為第i段剛體在坐標系Oixiyizi中的位置矢量;rk為第k段剛體的質心在坐標系Okxkykzk中的位置矢量。
將式(8)對時間求導,得到第k段剛體的質心在慣性系中的速度
(9)
則偏線速度
(10)
將式(9)代入式(10)得到剛體k對廣義速度yl的偏線速度

(11)
2.3 等效主動力(矩)及等效慣性力(矩)
忽略重力,以第k段剛體為例進行受力分析,第k段所受的主動力包括:左側有3個直線阻尼器的彈性變形力Fkz、3個旋轉阻尼器的彈性變形力矩Mkz、3個直線阻尼器的阻尼力Fukz、3個旋轉阻尼器的阻尼力矩Mukz,右側有3個直線阻尼器的彈性變形力Fky、3個旋轉阻尼器的彈性變形力矩Mky。
根據坐標變換矩陣及彈性變形力得到第k段剛體左右兩側阻尼器的彈性變形力
·diag(K1,K2,K3,K4)
(12)
式中:Fkz為第k段左側受到的彈性變形力;Mkz為第k段左側受到的彈性變形力矩;Fkv為第k段右側受到的彈性變形力;Mkv為第k段右側受到的彈性變形力矩;K1為左側直線阻尼器的彈性系數;K2為左側旋轉阻尼器的彈性系數;K3為右側直線阻尼器的彈性系數;K4為右側旋轉阻尼器的彈性系數。
各段質心所受的等效主動力Fkc和主動力矩Mkc為
(1) 基座(k=1)
漂浮基座左側沒有關節,僅受右側關節1 的作用力
(13)
式中:r1為基座質心到連體坐標系原點的距離。
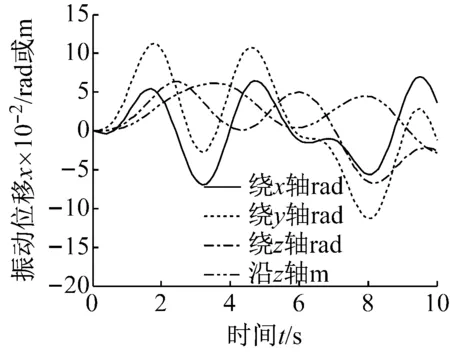
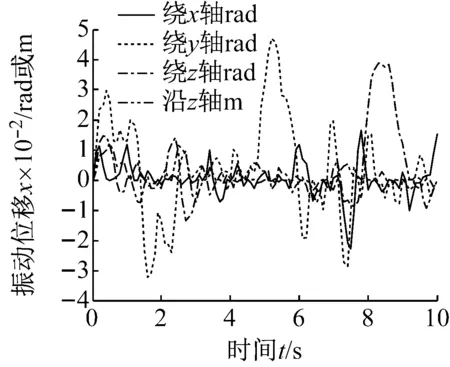
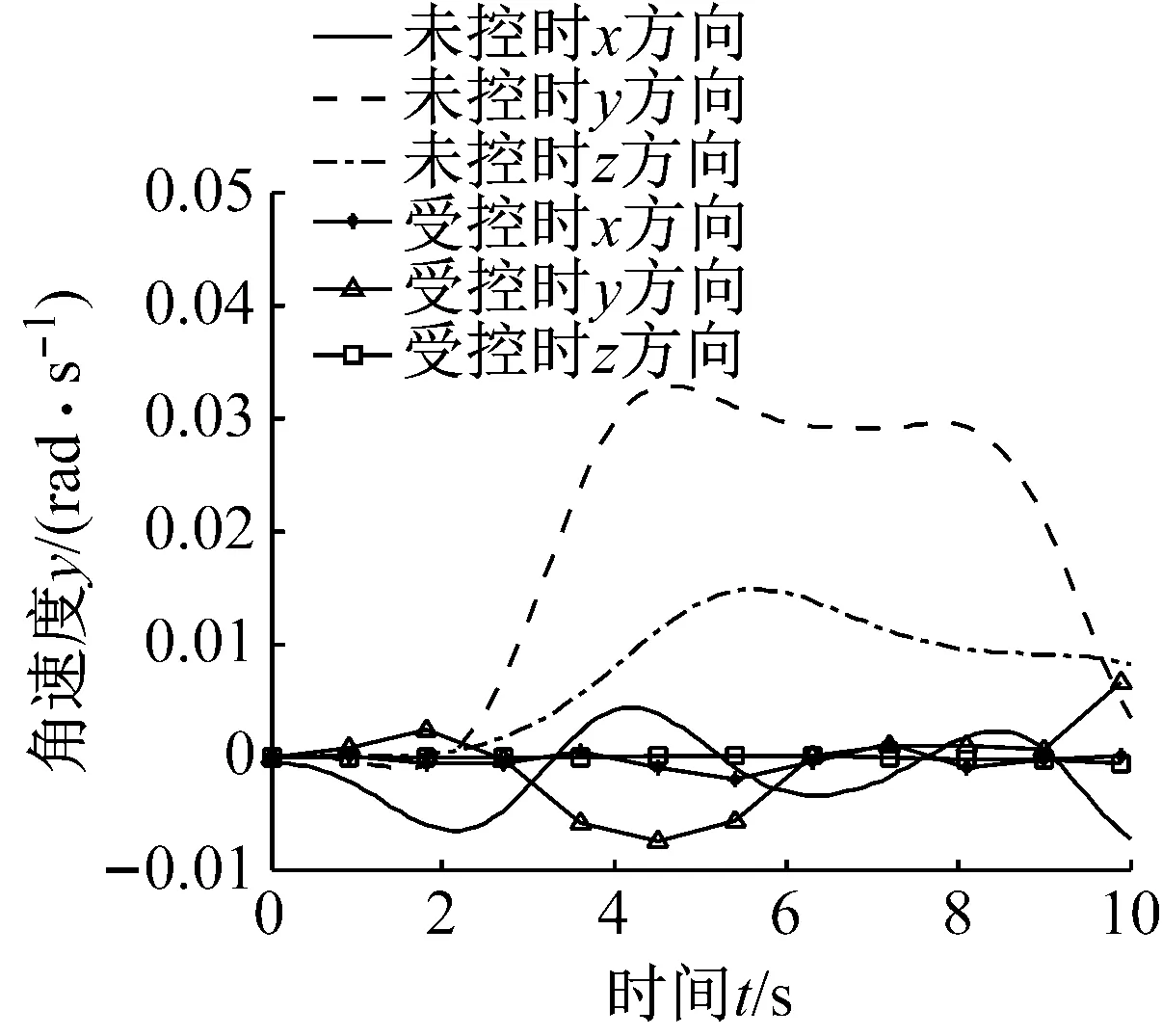
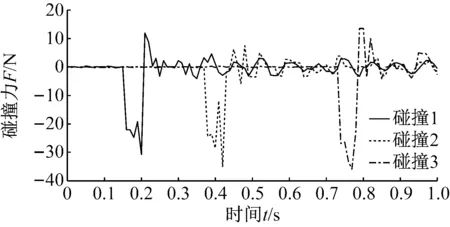
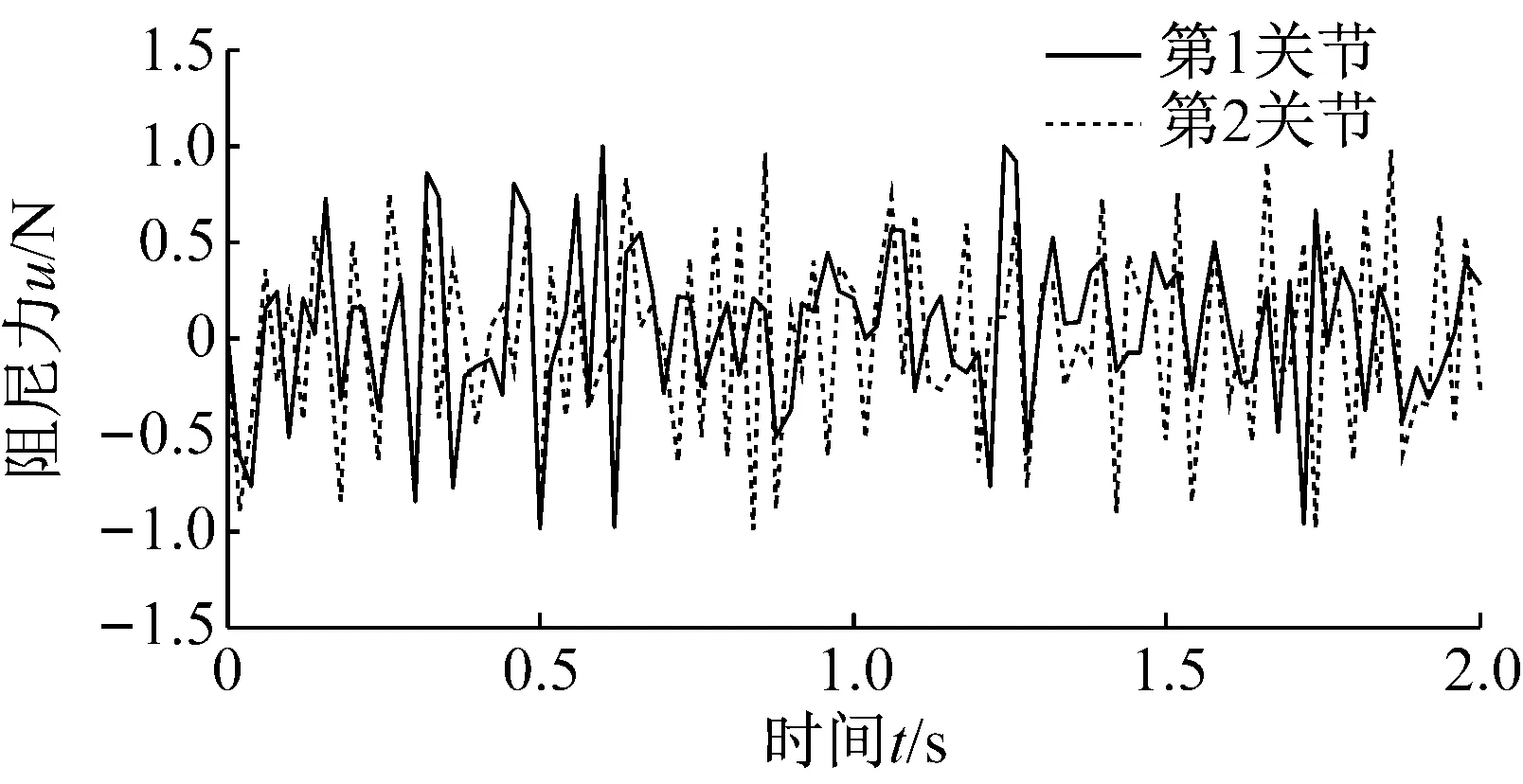
(2) 中間段(1 (14) 式中:Fkz=-F(k-1)y,Mkz=-M(k-1)y。 (3) 末端(k=N+1) (15) 式中:F為末端瞬時沖擊力;M為末端瞬時沖擊力矩。 對于包含(N+1)個剛體段的串聯型機構,其Kane動力學方程 (16) 式中:l=1, 2, 3, …, 6N+6。 將偏角速度,偏線速度,等效主動力(矩),等效慣性力(矩)代入式(16),并與運動學方程式(4)聯立,得到多級阻尼柔性抓捕機構的(6N+6)維非線性微分方程組 (17) 微粒群算法根據生物群覓食的思想,利用個體局部信息和群體全局信息指導搜索,通過不斷迭代優化自變量使得目標函數實現最優,對于大型復雜問題的優化有良好的適用性[13]。空間捕獲過程中,基座和柔性抓捕機構均可能因碰撞沖量引起失穩,此時,可通過優化控制多個阻尼器輸出的阻尼力來實現漂浮基與柔性抓捕機構整體系統的鎮定控制。 捕獲時的碰撞沖量會引發柔性抓捕機構的振動,進而在各個關節處產生彈性變形力(矩),且漂浮基座的位置和姿態會受到與其相連的關節處彈性變形力(矩)的影響,因此,完成捕獲后,漂浮基座與抓捕機構變成不穩定動力系統,而鎮定控制的目標即抑制該系統各個關節處的彈性變形量。目標函數可表示為 (18) 式中:n=6N,x1,x2,…,xn為抓捕機構各關節處沿6個方向的振動變形量,max(xn)為抓捕機構各關節處沿6個方向預先設定的最大允許振動變形量,可根據初始碰撞沖量及操作任務指標確定,當各關節處振動變形小于對應的最大允許振動位移時,即認為達到控制要求。a1,a2,…,an是加權系數,且滿足a1+a2+…+an=1。 由于傳統的微粒群算法容易陷入局部最小,故采用線性遞減、帶有慣性權重的微粒群進化算法進行優化計算,如式(19)所示,以便初始時刻快速搜索,快接近最優位置時,減慢搜索速度,加強局部搜索能力。 vij(t+1)=h·vij(t)+c1·rand1·[pij(t)-zij(t)]+ c2·rand2·[pgj(t)-zij(t)] zij(t+1)=vij(t+1)+zij(t) h=h2-c·(h2-h1) (19) 式中:vij(t)為微粒的飛行速度;zij(t)為微粒的當前位置;pij(t)為個體全局最好位置;pgj(t)為群體全局最好位置;c1為認知學習系數;c2為社會學習系數;c為系數;h∈[h1,h2]為慣性權重;正定常數rand1,rand2∈[0,1]為隨機數。 對于目標函數(18),當抓捕機構各關節處每個自由度方向的振動位移xi(i≤6N) 小于對應的最大允許振動變形量max(xi),即f(t)<1,說明鎮定控制已達到期望的要求,此時可終止微粒群迭代算法,并輸出該時刻求得的阻尼力,即為最優阻尼力。 具體的控制算法流程為 步驟1 根據初始時刻的碰撞動量和抓捕機構的 初始構型,由運動學方程(4)和動力學方程(17)計算t時刻抓捕機構的廣義坐標xl(t); 步驟2 由xl(t)和微粒群算法(19),通過以下迭代步驟(i)、(ii)和(iii)求解可得到t時刻可控阻尼器的最優阻尼力: (i) 定義微粒群規模m,根據可控阻尼器的數量確定粒子維數d,每個可控阻尼器的阻尼力大小對應微粒群中粒子的位置。初始化微粒群中每一個粒子的位置zij,將xl(t)和zij代入式(4)和(17),計算每個粒子(t+1)時刻的廣義坐標xl(t+1),并代入式(18)計算適應值Fg1,并將當前位置作為pij和pgj(t)。 (ii) 根據式(19)更新粒子的當前位置,并將xl(t)和代入式(4)、(17)、(18)繼續計算Fg2,比較Fg2和Fg1的大小,將適應值更小的粒子位置作為pij和pgj(t),并得到對應的Fg。 (iii) 判斷當前適應值Fg是否小于1。若不滿足要求,則重復步驟(ii)。若滿足要求,說明滿足算法終止條件,輸出當前的全局最好位置pgj(t),作為可控阻尼器t時刻的阻尼力u(t)。 步驟3 將u(t)和xl(t)代入式(4)和(17),計算(t+1)時刻抓捕機構的廣義坐標xl(t+1)。重復利用步驟2計算(t+1)時刻的最優阻尼力u(t+1),循環至終。 微粒群多級阻尼優化鎮定控制的流程框圖如圖2所示。 為驗證所提出方法的有效性,對某型3關節12自由度的抓捕機構進行多級阻尼鎮定控制仿真。由圖1可知,抓捕機構各個關節處沿Oixi、Oiyi直線方向的碰撞動量可通過多自由度機構的傳遞與轉換,由三個旋轉阻尼器間接鎮定,故只需保留Oizi軸的直線阻尼器。因此,該機構每個關節可設計4個自由度,分別是繞Oixi、Oiyi、Oizi軸的轉動自由度以及沿Oizi軸的直線運動自由度。在各個自由度方向上可安裝對應的直線或旋轉阻尼器,3關節抓捕機構共包含12個阻尼器。 圖2 微粒群多級阻尼優化鎮定控制流程圖 系統仿真參數:末端瞬時沖擊力F=(100,100,100)N,瞬時沖擊力矩M=(100,100,100) N·m。基座質量200 kg,慣性張量I1=diag (53.3,53.3,66.7)kg·m2。抓捕機構各連桿的質量mk=8 kg,慣性張量Ik=diag(2.5,2.5,5)kg·m2。旋轉式阻尼器的彈性系數K旋轉=40 N/m,阻尼力矩輸出范圍:Mu∈[-0.5,0.5]N·m,直線式阻尼器的彈性系數K直線=40 N/m,阻尼力輸出范圍:Fu∈[-0.5,0.5]N。微粒群規模:10,粒子維數:12,認知學習系數:c1∈[0.5,2.5]線性遞減,社會學習系數:c2∈[0.5,2.5]線性遞增,慣性系數:h∈[0.5,2.5]線性遞減,最大迭代次數:nmax=50。 分別對未施加控制和微粒群多級阻尼優化控制下的空間抓捕動力學進行仿真,對比施加控制前后抓捕機構和基座的動力學響應差異。圖3、圖5和圖7分別對應了柔性抓捕機構第1、第2和第3關節在未施加控制時的振動位移響應,圖4、圖6和圖8分別對應了柔性抓捕機構第1、第2和第3關節在施加多級阻尼鎮定控制后的振動位移響應。以第1關節的動力學響應為例進行對比分析可見,在末端碰撞力(矩)的作用下,未施加控制時第1關節的最大扭轉振動位移可達0.08 rad,最大直線振動位移可達0.06 m,而多級阻尼鎮定控制可以保證第1關節的最大扭轉振動位移減小至0.01 rad以內,最大直線振動位移減小至0.015 m以內。圖9給出了第1關節處四個阻尼器對應的最優阻尼力,均連續有界,表明利用本文控制方法求得的阻尼力是完全可控的。與第1關節的動力學響應規律類似,第2和第3關節處的振動位移均在多級阻尼控制的鎮定作用下實現了大幅度的收斂,實現了振動抑制。同理,圖10和圖11表明第2和第3關節處的四個阻尼器也能輸出連續有界的可控阻尼力。 圖12和圖13分別給出了受控前后基座在慣性坐標系下的質心位移和姿態角速度對比,可見,在多級阻尼的鎮定控制作用下,基座沿y軸方向的質心位移從未控時的最大值0.18 m減少至0.02 m,基座繞y軸的姿態角速度從未控時的最大值0.032 rad/s減少至0.007 rad/s,有效地規避了漂浮基座的姿態傾斜和角動量超限。 由上述仿真結果可知,采用多關節多自由度柔性抓捕機構完成空間捕獲任務,可大幅度減小碰撞沖量對基座的擾動,因而能保證基座的穩定性。同時,基于微粒群優化算法的多級阻尼鎮定控制策略能實現柔性抓捕機構在多維空間內的振動抑制。 圖3 無鎮定控制時第1關節的振動位移 Fig.3 Vibration displacements of 1st joints without stabilization control 圖4 多級阻尼鎮定控制時第1關節的振動位移 Fig.4 Vibration displacements of 1st joints with multistage damping stabilization control 圖5 無鎮定控制時第2關節的振動位移 Fig.5 Vibration displacements of 2nd joints without stabilization control 圖6 多級阻尼鎮定控制時第2關節的振動位移 Fig.6 Vibration displacements of 2nd joints with multistage damping stabilization control 圖7 無鎮定控制時第3關節的振動位移 Fig.7 Vibration displacements of 3rd joints without stabilization control 圖8 多級阻尼鎮定控制時第3關節的振動位移 Fig.8 Vibration displacements of 3rd joints with multistage damping stabilization control 圖9 多級阻尼鎮定控制時第1關節的阻尼力(矩) Fig.9 Damping forces (moments) of 1st joint in multi stage damping stabilization control 圖10 多級阻尼鎮定控制時第2關節的阻尼力(矩) Fig.10 Damping forces (moments) of 2nd joint in multi stage damping stabilization control 圖11 多級阻尼鎮定控制時第3關節的阻尼力(矩) Fig.11 Damping forces (moments) of 3rd joint in multi stage damping stabilization control 圖12 受控前后基座質心的位移 圖13 受控前后基座的角速度 選用SG-MRF2035型磁流變液,分別研制了直線式和旋轉式磁流變阻尼器,實物如圖14(a)和14 (b)所示,采用YH1718雙路穩壓穩流跟蹤電源對磁流變阻尼器進行“電流-阻尼力(矩)”伺服控制,經過測試實驗得知,直線式磁流變阻尼器的有效阻尼力輸出范圍為[-7.5,7.5]N, 旋轉式磁流變阻尼器的有效阻尼力矩輸出范圍為[-0.05,0.05]N·m。按照文獻[12]的結構設計方案研制了具有二關節四級阻尼的柔性抓捕機構原理樣機,實物如圖14(c)所示。將該柔性抓捕機構整體放置于水平氣浮平臺上,氣泵壓力設置為1.5 MPa,靠氣浮足噴出的高壓氣體反力來抵消機構自身的重力,此時可研究具有多級阻尼的柔性抓捕機構受到碰撞沖擊力后在水平面內的鎮定控制效果。 (a)直線式磁流變阻尼器(b)旋轉式磁流變阻尼器 (c) 柔性抓捕機構 Fig.14 Ground principle prototype of flexible capturing mechanism with two joint and four stage damping 實驗方案:柔性抓捕機構處于完全伸展狀態的直線位型,在其末端設計一個單擺裝置,利用重物塊下落至最低處時對柔性抓捕機構末端產生的沖擊力來模擬抓捕過程的碰撞力。在基座與柔性抓捕機構的連接法蘭處安裝ATI-Nano17型六維力傳感器,通過對該處耦合力的在線測量來驗證具有多級阻尼的柔性抓捕機構對基座擾動力的鎮定控制效果。在直線式磁流變阻尼器的運動軸端安裝RH100X30D05A型光柵尺用來測量該軸方向的直線振動位移,在旋轉式磁流變阻尼器的運動軸端安裝EAC58P軸套型絕對值編碼器用來測量該軸方向的旋轉振動位移。 若單擺裝置的重物塊質量為m,固定擺長為l,則當重物塊以初始角度θ落下時,重物塊在最低點獲得的動量為 設碰撞后單擺彈回的角度為β,則碰撞后重物塊的動量為 此時,可計算抓捕機構末端受到的碰撞力為 式中:Δt為碰撞時間,可通過力傳感器獲得。 重物塊質量m=2.0 kg,固定擺長l=203 mm,以θ=30°作為初始角度釋放單擺重物,通過測量磁流變阻尼器分別在斷電和伺服狀態下六維力傳感器的碰撞力數值,開展無多級阻尼和有多級阻尼狀態下的鎮定控制對比實驗,連續進行碰撞實驗各三次,實驗結果如圖15所示。由圖15(a)可以看出,磁流變阻尼器在斷電狀態下,抓捕機構末端的碰撞力對基座的擾動力平均值約為200 N,最大值約為261 N。由圖15(b)可以看出,磁流變阻尼器在伺服狀態下,抓捕機構末端碰撞力對基座的擾動力平均值約為35 N,最大值約為37.5 N。圖15(c)表明在抓捕機構的當前位型和碰撞力作用下,第1關節和第2關節內的旋轉式磁流變阻尼器均無輸出,由直線式磁流變阻尼器起主導作用,且其輸出阻尼力連續有界,相應地,圖15(d)給出了第1關節和第2關節內直線式磁流變阻尼器對應軸的振動位移,取三次實驗的平均值,可見,在多級阻尼器作用下,各關節對應軸的振動位移漸進收斂。 (a) 磁流變阻尼器斷電狀態下基座受到的擾動力 (b) 磁流變阻尼器伺服狀態下基座受到的擾動力 (c) 直線式磁流變阻尼器伺服狀態下輸出的阻尼力 (d) 磁流變阻尼器伺服狀態下兩關節的直線振動位移 Fig.15 Collision simulation test results of two-joint four-stage damping flexible capturing mechanism 該實驗結果表明具有多級阻尼的柔性抓捕機構可大幅度減小碰撞沖量對基座的擾動,對規避漂浮基座的姿態傾斜和角動量超限可起到積極作用。同時,柔性抓捕機構各個關節的振動位移在多級阻尼的作用下均漸進收斂,能保證系統的整體鎮定。 (1) 提出了一種具有多級可控阻尼的串聯型柔性抓捕機構廣義模型,用以實現空間捕獲任務的柔順化。 (2) 通過在柔性抓捕機構的關節處設計多維可控阻尼器,可以實現對空間任意方向碰撞沖量的緩沖和卸載。 (3) 采用微粒群優化算法可以實現多級阻尼的優化配置,保證基座穩定的同時實現柔性機構的振動抑制,最終完成系統的鎮定控制。 [1] XU W L, YUE S G. Pre-posed configuration of flexible redundant robot manipulators for impact vibration alleviating[J]. IEEE Transactions on Industrial Electronics, 2004, 51(1): 195-200. [2] 叢佩超, 孫兆偉. 空間機械臂捕捉空間目標分析[J]. 上海航天, 2009(4):7-11. CONG Peichao, SUN Zhaowei. The research of free-floating space manipulator capture object[J]. Aerospace Shanghai, 2009(4): 7-11. [3] WEI Cheng, LIU Tianxi, ZHAO Yang. Grasping strategy in space robot capturing floating target[J]. Chinese Journal of Aeronautics, 2010, 23(5): 591-598. [4] LIU Shengping, WU Licheng, LU Zhen. Impact dynamics and control of a flexible dual-arm space robot capturing an object[J]. Applied Mathematics and Computation, 2007, 185(2): 1149-1159. [5] DONG Qiuhuang, CHEN Li. Impact dynamics analysis of free-floating space manipulator capturing satellite on orbit and robust adaptive compound control algorithm design for suppressing motion[J]. Applied Mathematics and Mechanics, 2014, 35(4): 413-422. [6] 董楸煌, 陳力. 柔性空間機械臂捕獲衛星碰撞動力學分析、鎮定運動神經網絡控制及抑振[J]. 機械工程學報, 2014, 50(9): 34-42. DONG Qiuhuang, CHEN Li. The impact dynamics analysis of flexible space manipulator capturing a satellite and neural network calming motion control and vibration suppression[J]. Journal of Mechanical Engineering, 2014, 50(9): 34-42. [7] CHU Ming, CHEN Gang, JIA Qingxuan, et al. Simultaneous positioning and non-minimum phase vibration suppression of slewing flexible-link manipulator using only joint actuator[J]. Journal of Vibration and Control,2014,20(10): 1488-1497. [8] BIAN Yushu, GAO Zhihui. Impact vibration attenuation for a flexible robotic manipulator through transfer and dissipation of energy[J]. Shock and Vibration, 2013, 20(4): 665-680. [9] CHU Ming, ZHANG Yanheng, CHEN Gang, et al. Effects of joint controller on analytical modal analysis of rotational flexible manipulator[J]. Chinese Journal of Mechanical Engineering, 2015, 28(3): 460-469. [10] BALAMURUGAN L, JANCIRANI J, ELTANTAWIE M A. Generalized magnetorheological (MR) damper model and its application in semi-active control of vehicle suspension system[J]. International Journal of Automotive Technology, 2014, 15(3): 419-427. [11] NGUYEN H, THAI C, SHARF I. Capture of spinning target with space manipulator using magneto rheological damper[C]//AIAA Guidance, Navigation, and Control Conference. Toronto, Canada:American Institute of Aeronautics and Astronautics Inc., 2010. [12] 褚明, 董正宏, 孟慶川, 等. 基于十字軸結構的軟接觸關節: ZL201410784247.7[P]. 2014-12-16. [13] 郭迎慶, 徐趙東, 費樹岷, 等. 磁流變智能結構的微粒群優化控制[J]. 振動與沖擊, 2011,30(9): 59-63. GUO Yingqing, XU Zhaodong, FEI Shumin, et al. PSO control used in magnetorheologicaI intelligent structures[J]. Journal of Vibration and Shock, 2011,30(9): 59-63.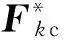
2.4 動力學方程
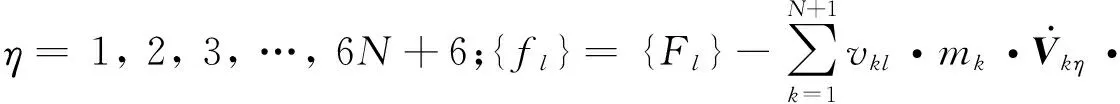
3 基于微粒群的多級阻尼優化控制
3.1 微粒群算法的適應度函數
3.2 多級阻尼優化的鎮定控制
4 數值仿真









5 實驗驗證




6 結 論

