四邊自由矩形板橫向振動的近似解及其實驗

付江松， 徐 鑒(同濟大學 航空航天與力學學院， 上海 200092)

在航空航天領域中，太陽能帆板的作用至關重要。對于遠離航天器的矩形太陽能帆板，其邊界條件可視為四邊自由。因此，太陽能帆板的振動在某種程度上可以看作是四邊自由矩形板的振動問題。但在實際工程中，四邊自由矩形板的振動問題難度比較突出。這種難度主要表現在其振型函數沒有精確解，進而對板固有頻率和振型的計算帶來很大困難。

航天器進入太空后，太陽能帆板大多暴露在航天器外部，很容易在外力作用下產生振動。如果外激勵頻率接近板的固有頻率，就會引起共振，這是我們要竭力避免的后果。因此，為了避開共振區，尋找四邊自由矩形板振型函數的一種近似解及固有頻率計算公式是十分必要的。

關于矩形板的振動問題在國內外各類文獻中被廣泛研究，例如Mindlin[1]于1951年研究了關于邊界自由厚板的橫向振動問題并得到了一些解析解。Chang等[2]使用伽遼金單模態近似方法研究了各向異性矩形板的自由振動。Eslami等[3-4]運用多尺度法與單模態和雙模態伽遼金法，研究了簡支邊界條件下各向異性板的強迫振動問題。Mochida等[5]分析了邊界自由矩形板固有頻率的上下界限問題。Wang[6]通過改進的Ritz法研究了帶圓角矩形板的振型函數。許琪樓[7-8]通過引入附加振型，構造了新的振型函數表達式，提出了一種關于有角點支座的矩形板自由振動分析的新方法。曾軍才等[9]采用改進的Fourier級數方法，研究了正交各向異性矩形薄板的彎曲振動問題。

然而其中針對四邊自由矩形板振型函數和固有頻率精確解的研究相對較少，其原因在于很難找到一個既滿足平板彎曲控制方程又滿足自由邊界條件的振型函數表達式。目前的處理方法大多都是通過尋找振型函數的近似解，從而求解板的固有頻率。在近似解的選取方式上，曹志遠[10]提出了一種雙向梁函數的級數組合，作為板的振型函數近似解，但缺乏實驗結果的比較。方奕忠等[11]采用了另一種組合級數表示了板的振型函數近似解，并通過實驗對近似解進行了驗證。然而該近似解的精確程度并不理想。本文在以往學者所提供思路的啟發下，從矩形板基本控制方程出發，通過對實驗結果的擬合，找到了一種滿足精度要求的四邊自由矩形板的近似解。

1 薄板的控制微分方程

本文所研究的矩形板的模型如圖1所示，板結構的四個邊界處均為自由。

圖1 矩形薄板模型

根據薄板振動理論，矩形板自由振動的控制方程為

(1)

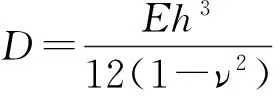
本文研究四邊自由矩形板，其邊界條件滿足：

在x=0,a自由邊界上，有

(2)

在y=0,a自由邊界上，有

(3)

2 實驗方法的驗證

在四邊自由矩形板振型函數近似解驗證方法的選取上，我們采用克拉尼斑圖[12]實驗方法。該方法可得到板的二維駐波圖形(克拉尼斑圖)。

為了驗證克拉尼斑圖實驗方法的正確性，我們通過該方法得到了邊界自由圓板的二維駐波圖形。再將其與由邊界自由圓板精確解所求出的理論駐波圖形相比較，從而驗證其正確性。圖2為邊界自由圓板橫向振動實驗裝置。

圖2 邊界自由圓板實驗裝置

對于邊界自由的圓板，其振型函數表達式為

W(r,θ)=[C1Jn(αr)+C2In(αr)]cosnθ

(4)

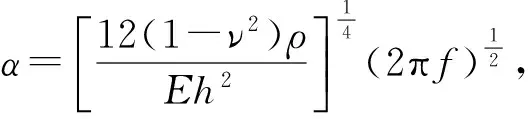
將自由邊界條件

(Mr)r=r0=0，

(5)

代入式(4)可得關于參數α的頻率方程，并解得若干α。將得到的α代入圓板的固有頻率計算公式

(6)

求出其各階固有頻率，進而解出圓板的二維駐波理論圖形[13]并與實驗結果相比較。二者對比結果如表1。各種計算參數為E=71 GPa，ν=0.33，ρ=2 830 kg/m3，圓板半徑r0=150 mm，h=0.9 mm。

從表1的結果可以看到，理論結果與實驗結果接近并滿足精度要求，說明由克拉尼斑圖實驗方法所得到的二維駐波圖形結果是可靠的。

表1 理論駐波圖形與實驗駐波圖形對比結果

3 四邊自由矩形板振型函數的近似解

對于四邊自由矩形板的振動問題，我們將控制方程(1)的解表示為

w=W(x,y)(Acosωt+Bsinωt)

(7)

式中：W(x,y)即為板的主振型函數。將式(7)代入微分方程式(1)及邊界條件式(2)，(3)中，得到有關主振型的振動微分方程

(8)

(9)

(10)

在四邊自由矩形板振型函數的選取問題上，目前尚沒有既滿足微分方程式(8)，又滿足邊界條件式(9)，(10)的精確解存在。因此，本文選取了式(11)和式(12)兩種形式的組合級數，并利用這兩種級數組合出本文的近似解。

式(11)表達式如下

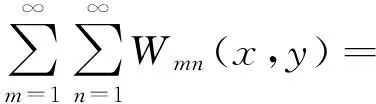
(11)

其中Amn為待定系數，用來調整不同階次的組合級數以逼近矩形板振型函數真實解。

式(12)表達式如下

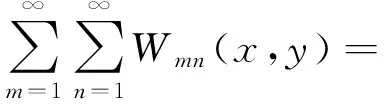
(12)

其中

W1mn=A1mn(cosβmx+B1sinβmx)×

(cosβny+D1sinβny),

W2mn=A2mn(coshβmx+B2sinhβmx)×

(coshβny+D2sinhβny)

(13)

在式(11)中，Xm(x)和Yn(y)分別取為邊界自由梁的第m階和第n階振型函數。顯然式(11)滿足邊界條件(9)，(10)。按照文獻[10]中的方法，將振型函數(11)代入微分方程式(8)中，通過求解頻率方程我們得到了矩形板第(m,n)階固有圓頻率計算式

(14)

在式(12)中，Wmn(x,y)為板的第(m,n)階振型函數。將式代入微分方程及邊界條件可得，表達式滿足微分方程，但不滿足邊界條件。式中A1mn，B1，D1，A2mn，B2，D2，βm，βn為待定參數。

由于式(12)不能滿足所有的邊界條件式(9)和(10)，為了求解其中的待定系數，我們將四邊自由的邊界條件弱化為四角點自由。即將邊界條件式(9)和(10)改寫為如下形式

(15)

(16)

(17)

(18)

將Wmn=W1mn+W2mn代入邊界條件式(15)至式(18)中可解得

其中可令A1mn=A2mn=Amn。

由式(21)可知，βm與βn均由方程

cos(βa)cosh(βa)=1

(22)

(23)

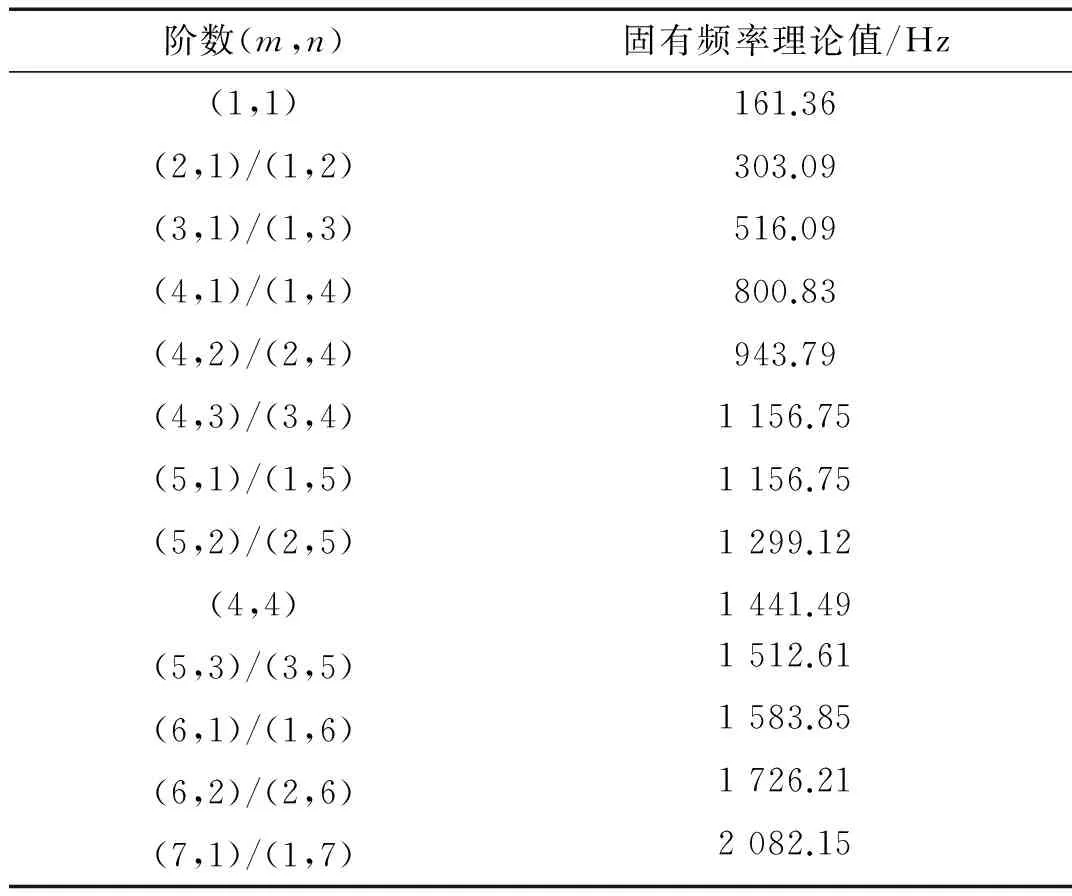
表2 矩形板理論固有頻率

從實驗中我們發現，板的第(m,n)階振型函數的近似解，在m+n為偶數時，取為式較為合適；m+n為奇數時，應取為式(12)。因此板的振型函數近似解可由式(11)與式(12)組合而成。而在實際工程應用中，由于式(11)與式(12)為無窮級數的形式，需要對其進行簡化。經過數值計算與實驗結果的對比我們發現，第(m,n)階固有頻率下的振型函數近似解W(x,y)可以用第(m,n)階振型函數Wmn(x,y)與附近幾階振型函數疊加后近似表示。因此我們將第(m,n)階固有頻率下振型函數表達式取為

(24)

其中

(25)

(26)

(27)

在式(25)與式(26)中，各項級數前的參數Aij為常數。而Aij的值原本由邊界條件確定，但由于近似解無法滿足所有的邊界條件，我們通過對實驗結果的擬合，給出了關于常數Aij的一種經驗公式，式(28)與式(29)

其中fmn為第(m,n)階固有頻率值。

在表達式(28)，(29)中，Aij的大小反應了該階振型函數在近似解中所占的比重。從能量角度來講，越接近第(m,n)階固有頻率的振型越容易被激發，在近似解中所占的比重也應該越大。因此常數Aij的大小與該項級數所對應的主振型函數的固有頻率fij，第(m,n)階固有頻率fmn有關。即認為越遠離共振頻率的振型函數前的常數Aij越小，在整個近似解中所占比重也越小，這一性質也與矩形板結構在實際工程和實驗中的表現相

吻合。

4 近似解與實驗解的比較

通過近似解表達式(24)，我們可以得到四邊自由矩形板二維駐波理論圖形。利用克拉尼斑圖實驗方法，可以得到矩形板的二維駐波實驗圖形。

通過對比理論圖形與實驗圖形之間的相似程度，我們可以評價近似解的近似程度。表3為各階固有頻率下四邊自由矩形板的二維駐波理論圖形與實驗圖形以及二者所對應的固有頻率值之間的比較。

表3 近似解理論圖形(右)與實驗圖形(左)對比

續表3

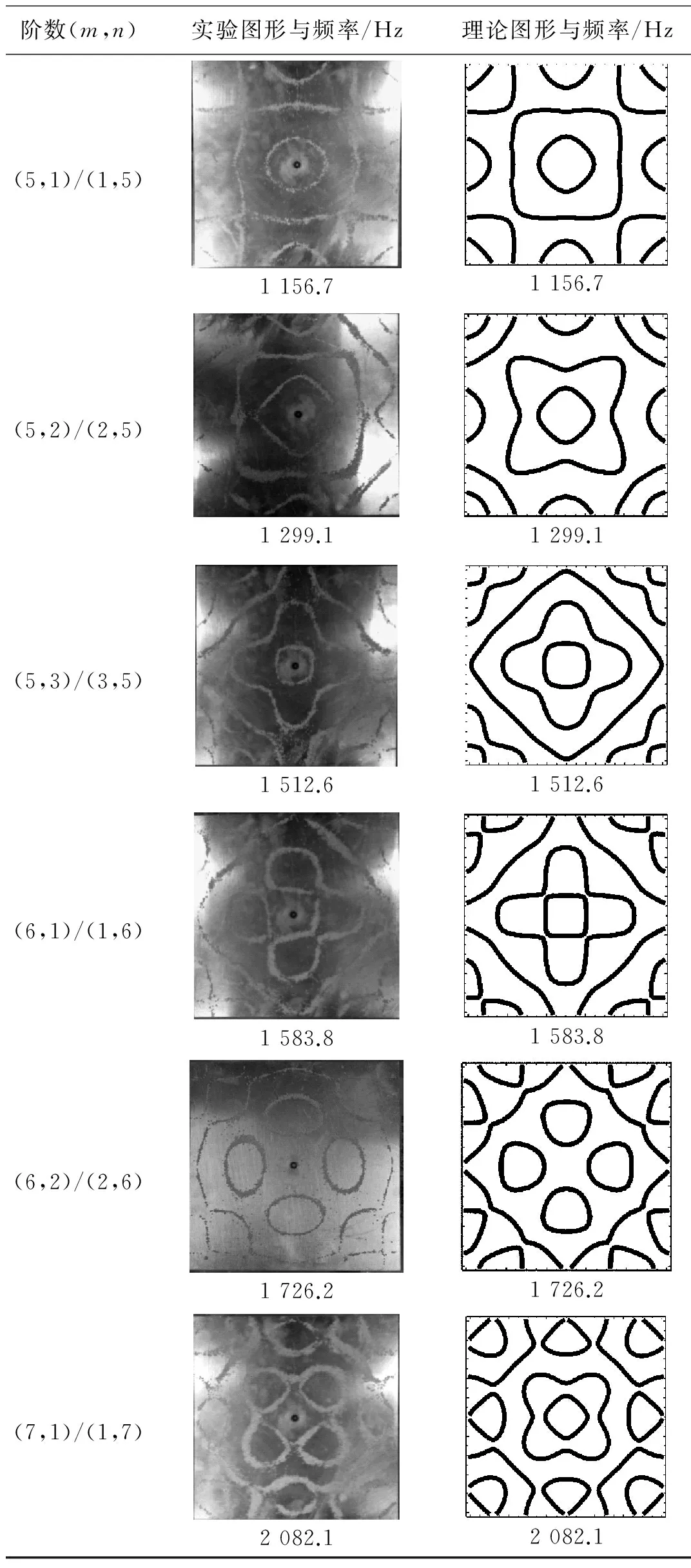
階數(m,n)實驗圖形與頻率/Hz理論圖形與頻率/Hz(5,1)/(1,5)1156.71156.7(5,2)/(2,5)1299.11299.1(5,3)/(3,5)1512.61512.6(6,1)/(1,6)1583.81583.8(6,2)/(2,6)1726.21726.2(7,1)/(1,7)2082.12082.1

通過表3所示結果，我們可以看到由固有頻率表達式所計算出的結果與實驗測得的固有頻率基本一致。近似解所得到的二維駐波圖形與實驗結果雖然無法完全吻合，但兩者在2 000 Hz內的階駐波圖形拓撲結構上均吻合良好，這足以證明本文所得近似解對精確解有著良好的近似。因此，本文所給出的近似解式是可信的且滿足精度要求。

5 結 論

本文構造了四邊自由矩形板橫向振動的近似解。為了驗證所構造近似解的有效性，搭建了四邊自由矩形薄板橫向振動的實驗平臺。首先通過與邊界自由圓板振型函數的比較，驗證了克拉尼實驗方法的正確性和可靠性。在此基礎上，通過實驗得到了四邊自由矩形板在0～2 000 Hz頻帶內的一系列二維駐波圖形(克拉尼圖形)，將實驗結果(克拉尼斑圖)與本文構造的近似解所得駐波圖形相比，發現兩者從定性、定量兩方面均吻合得較好，從而驗證了本文提出的近似解有效性。

值得注意的是，本文構造的Aij的表達式(28)和(29)僅僅是通過大量的實驗結果比對得出的，因此是一種經驗性公式。關于Aij表達式的優化問題，還需要投入更多的研究。

[1] MINDLIN R D. Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates[J]. J of Appl Mech, 1951, 18(1):31-38.

[2] CHANG W P, SHOOU-CHIAN J. Nonlinear free vibration of heated orthotropic rectangular plates[J]. International Journal of Solids & Structures, 1986, 22(3):267-281.

[3] ESLAMI H, KANDIL O A. Nonlinear forced vibration of orthotropic rectangular plates using the method of multiple scales[J]. Aiaa Journal, 1971, 27(7):955-960.

[4] ESLAMI H, KANDIL O A. Two-mode nonlinear vibration of orthotropic plates using method of multiple scales[J]. AIAA Journal, 1989, 27(7):961-967.

[5] MOCHIDA Y, ILANKO S. Bounded natural frequencies of completely free rectangular plates[J]. Journal of Sound & Vibration, 2008, 311(1/2):1-8.

[6] WANG C Y. Vibrations of completely free rounded regular polygonal plates[J]. International Journal of Acoustics & Vibrations, 2015, 20(2):107-112.

[7] 許琪樓. 四角點支承四邊自由矩形板自振分析新方法[J]. 振動與沖擊, 2013, 32(3):83-86.

XU Qilou. A new analysis method for free vibration of a rectangular plate with 4-free-edges and 4 corner point supportsclamped[J]. Joumal of Vibration and Shock, 2013, 32(3):83-86.

[8] 許琪樓.有角點支座矩形板自振分析[J]. 振動與沖擊, 2013, 32(17):84-89.

XU Qilou. Free Vibration analysis of a rectangular plate with corner point supports[J]. Joumal of Vibration and Shock, 2013, 32(17):84-89.

[9] 曾軍才, 王久法, 姚望,等. 正交各向異性矩形板的自由振動特性分析[J]. 振動與沖擊, 2015, 34(24):123-127.

ZENG Juncai, WANG Jiufa, YAO Wang, et al.Free vibration characteristics of orthotropic rectangular plates[J]. Joumal of Vibration and Shock, 2015, 34(24):123-127.

[10] 曹志遠. 不同邊界條件功能梯度矩形板固有頻率解的一般表達式[J]. 復合材料學報, 2005, 22(5):172-177.

CAO Zhiyuan. Unified expression of natural frequency solutions for functionally graded composite rectangular plates under various boundary conditions[J]. Acta Materiae Compositae Sinica, 2005, 22(5):172-177.

[11] 方奕忠,王鋼,沈韓,等.方形薄板二維駐波的研究[J].物理實驗,2014,34(1):33-36.

FANG Yizhong, WANG Gang, SHEN Han, et al. Research of 2-dimensional standing waves in square plate[J]. Physics Experimentation, 2014,34(1):33-36.

[12] ROSSING T D. Chladni’s law for vibrating plates[J]. American Journal of Physics, 1982, 50(3):271-274.

[13] 王繼超, 王慧. Chladni圖案的MATLAB模擬[J]. 實驗科學與技術, 2011, 9(2):181-183.

WANG Jichao, WAHG Hui. Simlation of Chladni patterns with MATLAB[J]. Experiment Science and Technology, 2011, 9(2):181-183.