牛頭刨床六桿機構的虛擬樣機建模與仿真分析

宋克偉 姚文莉 郝 鑫 李貞靖

（青島理工大學 理學院，青島 266520）

牛頭刨床是一種金屬切削加工設備，利用往復運動的刀具切削固定在機床工作平臺上的工件。其主運動為電動機→變速機構→搖桿機構→滑枕往復運動。主運動表現出明顯的急回特性，即要求滑枕在工作行程中速度低，工作回程時急速返回，對此，僅憑經驗很難對運行時的位移、速度及加速度和作用力的特征進行判斷[1-3]。對牛頭刨床六桿機構運行時的以上可測參數以圖像形式輸出，并分析各運動副中的受力就顯得非常有必要。

以往對牛頭刨床六桿機構的研究主要偏向于對其運動學及優化進行分析。伍平主要針對多體系統建立動力學方程模型并進行數值求解[4]。湯萍等利用實例機構，分析了機械系統的某一角速度建模求解過程[5]。此外，有學者論述了運用ADAMS軟件建立牛頭刨床機構的幾何建模過程，并對其運動學進行仿真分析[6-7]。趙玉成等利用Pro/E對牛頭刨床進行了動力學分析并得到各運動副連接處的作用反力曲線[8]。本文基于全局坐標系，利用各構件轉動副之間的坐標關系建立滑枕運動至不同位置時的運動學方程，采用分離體法和圖解法添加不同工況下的切削阻力對機構進行應力分析，應用ADAMS進行動力學仿真，以貼近工程實際并為多體系統動力學的建模過程提供典型的實例分析。

1 模型的建立

針對一種牛頭刨床機構簡圖，本文建立了直角坐標系，如圖1所示。其中，構件1為曲柄，與水平方向的夾角為θ，作為原動件為整個機構提供動力，最終實現構件5的直線往復運動。曲柄BC的連續回轉運動帶動擺桿AD的往復擺動，通過連桿DE帶動滑枕EF作直線往復運動，從而實現刀具G在工件上作切削運動。其中，C1和C2、D1和D2分別為擺桿AD運動至極限位置時同一鉸鏈點的不同狀態。

2 運動學分析

2.1 運動方程的建立

平面機構自由度的計算公式為：F=3n-（2pl+ph），在該機構圖中n=5，低副數量pl=7，高副數量ph=0，即整個機構自由度數F=1，其自由度數與原動件數目相同，符合機構具有確定運動的條件。

機構簡圖中擺桿AD與x軸正方向夾角為φ，根據各構件的位置關系可以確定如下坐標關系B（0，l1），C（l1cos，l2-l1sinθ），D（l3cosφ，l3sinφ）。 因 此 矢 量 AC =（l1cosθ,l2-l1sinθ）。

圖1 牛頭刨床六桿機構運動簡圖

則夾角φ可表示為：

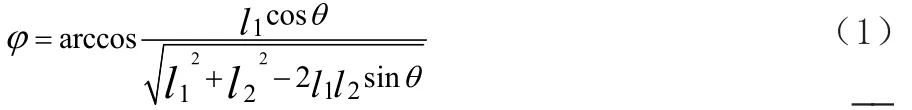
假 設 E點 坐 標 為（x，l5）， 則 矢 量 DE=（x-l3cosφ,l5-l3sinφ）。

因此構件4的長度計算公式為：

整理可得，滑枕位置的函數方程為：

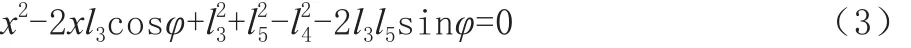
式中，角度φ與角度θ有關，θ與時間t有關。

對式（3）兩邊求導，得到其速度方程為：

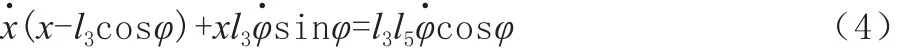
同理，對式（4）兩邊求導，得到其加速度方程為：

綜上分析和計算，同時得到了滑枕EF的位移、速度和加速度運動方程。

2.2 運動學建模與仿真

2.2.1 建模

在ADAMS軟件中建立牛頭刨床模型時，各構件參數 應 符 合 如 下 要 求：l1=140mm；l2=280mm；l3=600mm；l4=l3/4=150mm；l5=650mm。

擺桿AD的擺動幅度為60°，刨床運動具有明顯的急回特性，當曲柄BC以一定角速度逆時針轉動，擺桿由右極限位置運動至左極限位置時，刀具G處于工作行程；反之，刀具G處于工作回程。根據以上數據及相關要求，建立模型，如圖2所示。

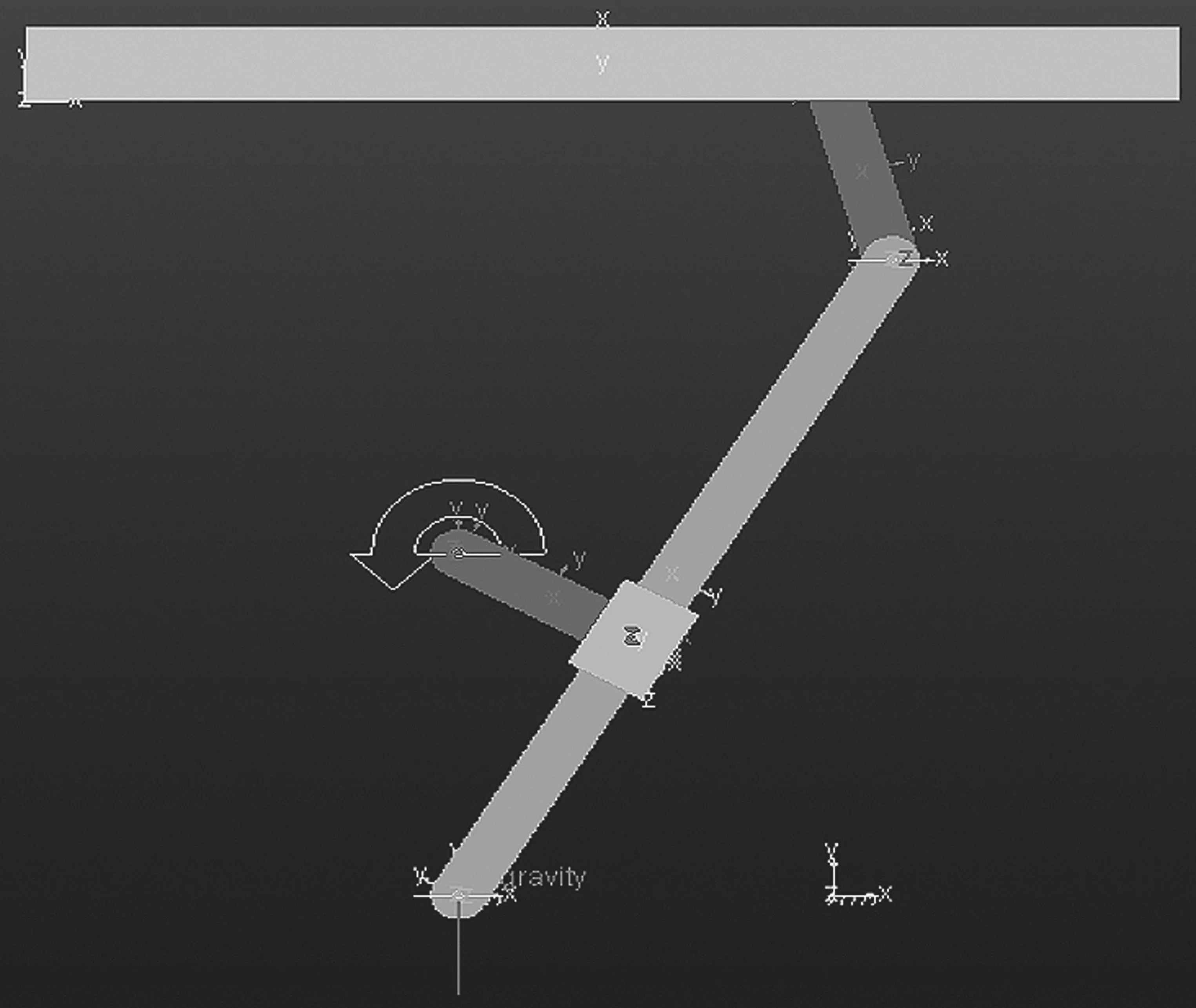
圖2 牛頭刨床六桿機構虛擬樣機模型

2.2.2 仿真及后處理

進入仿真及后處理模塊，設置曲柄1的角速度ω=π/6rad/s，即其周期為T=2π/ω=12s，設置仿真時間15s，仿真步數500步進行運動仿真。仿真結束測量曲柄1、擺桿AD的轉角，滑枕位移、速度和加速度隨時間變化規律，并輸出曲線圖，如圖3所示。

通過對圖像的綜合分析，筆者發現，滑枕上E點最大位移和最小位移分別為-349mm、259mm，其行程為608mm。當刨床處于工作行程時，曲柄運行角度為θ1，工作回程時運行角度為θ2，θ1＞θ2，并且曲柄角速度ω恒定不變，因此工作回程時速度遠遠大于工作行程時速度，刨床獲得較為明顯的急回特征。將刨床尺寸參數分別代入式（3）、式（4）、式（5），其計算數據符合機構運動的特征曲線，仿真具有正確性。

3 動力學分析

3.1 數學模型的建立

根據前述運動學分析可以求得滑枕的慣性力Fi5，若只考慮滑枕質量G5、慣性力Fi5和切屑阻力Fr，可應用圖解法和分離體法求解各運動副中的反力和加于原動件上的平衡力偶距。各構件受力如圖4所示。

桿組4、5受力情況如圖4（a）所示，根據矢量關系列平衡方程如下：

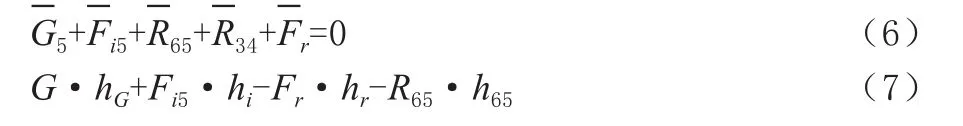
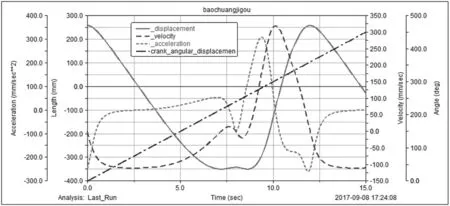
圖3 原動件轉角與滑枕E點運動曲線

桿組3、4受力情況如圖4（b）所示，列出矢量方程為：

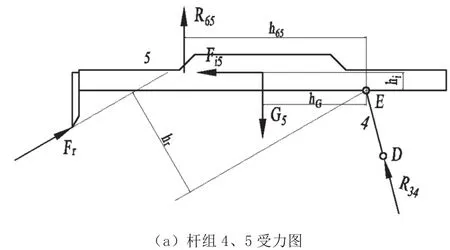
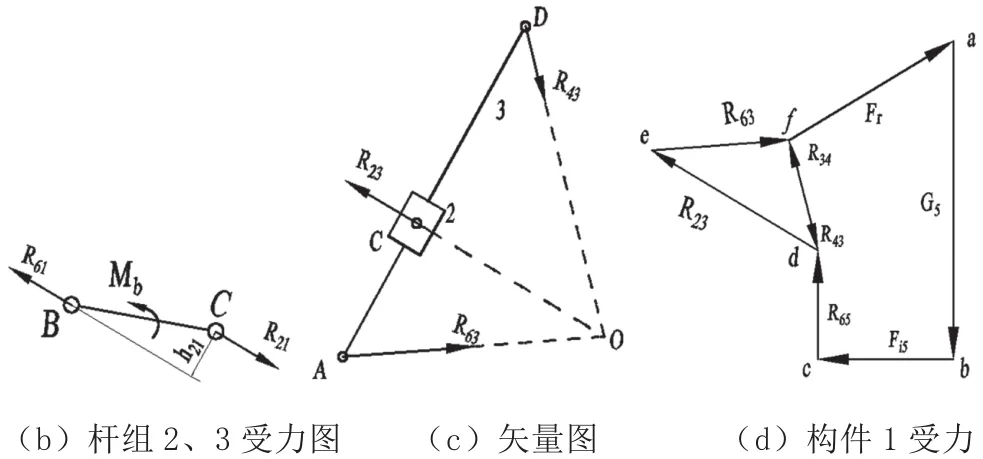
圖4 構件受力分析

取一定比例μl按照圖解法繪出矢量圖，如圖4（c）所示。矢量圖中各線段長度即代表對應力的比例大小。以構件1為示力體，其受力情況如圖4（d）所示，求得平衡力矩Mb=-R21h21，方向與ω相同。

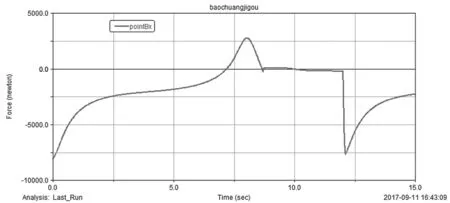
圖5 轉動副B處約束反力Fx

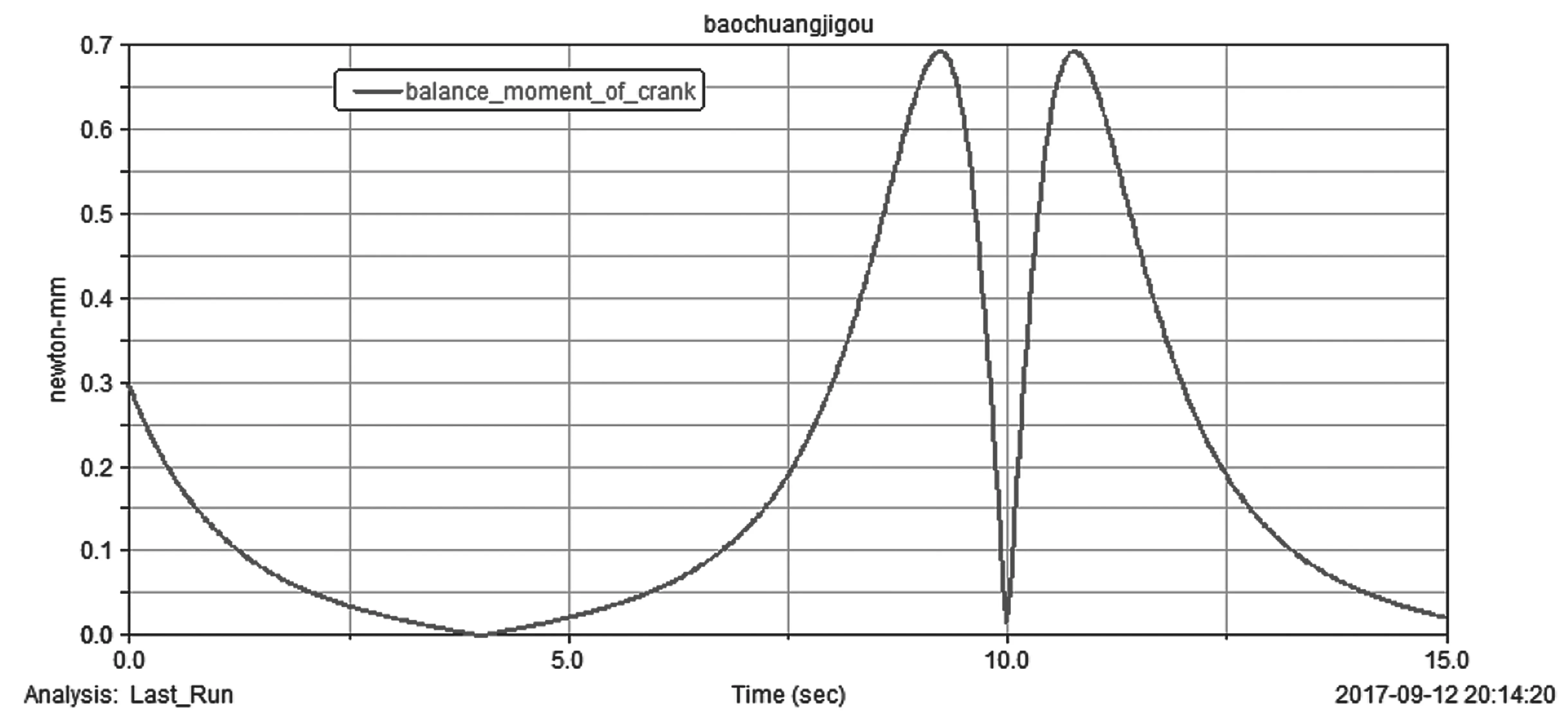
圖6 構件1平衡力矩Md

3.2 動力學建模與仿真

按照已知條件設置構件的質量信息和轉動慣量信息，并在刀具G處添加切削阻力Fr，完成動力學建模的設置。仿真后輸出支座反力曲線如圖5所示，構件1平衡力矩曲線如圖6所示。

通過仿真并分析支反力曲線圖，發現刨床在工作行程時支反力較大，回程時相對平穩，推得刨床在工作行程時整個機床會產生較大的震動和沖擊。刨床處于工作行程時，平衡力矩相對更平穩，回程中力矩波動幅度大且最大力矩出現在切削阻力出現和消失時，符合實際運行需要。

4 結語

對機構進行理論分析和仿真分析，驗證了模型的正確性，同時較為直觀地展現出刨床處于工作行程時滑枕的速度變化平穩，加速度值也較小，工作回程時速度變化幅度大，加速度值較大，具有明顯的急回特性。研究成果可為六桿機構的優化設計提供技術指導，為其他類似機構的運動學和動力學問題的分析提供借鑒。利用虛擬樣機技術在概念設計階段，通過科學理論和計算機語言，對設計階段的產品進行虛擬性能測試，達到提高性能、降低設計成本和減少產品開發時間的目的。