三星時差定位系統的有源校正算法

任凱強，孫正波

(盲信號處理重點實驗室， 成都 610041)

0　引　言

三星時差定位系統是星載無源定位的重要手段之一，其原理是利用輻射源信號到達三顆衛星的到達時間差實現對輻射源的定位，具有定位精度高、作用距離遠、隱蔽性好等優點，廣泛應用于移動通信和衛星導航等領域[1-2]。在實際應用中，由于星歷誤差和時間同步誤差的存在，嚴重影響了三星時差定位系統的定位精度[3-6]。

文獻[7-12]提出可引入已知位置的參考源來消除時差定位系統中星歷誤差和時間同步誤差對定位精度的影響。文獻[7-9]僅考慮了對星歷誤差的校正，沒有考慮對時間同步誤差的校正，這些方法均是利用參考源信號的觀測信息直接對星歷誤差進行估計，由于待估計參數過多，該類算法在參考源較少時，校正精度和穩健性都不理想；文獻[10]提出利用正交投影消除雙星時頻差定位系統中的時頻差測量系統偏差；文獻[11]提出了一種三星時差系統的四站標定方法，該方法通過解方程的方式求解出副星相對位置誤差和時間同步誤差并實現校正，但由于沒有考慮TDOA觀測噪聲和星歷誤差的統計信息，該方法不是最優的，且該算法需要四個參考源才能實現誤差校正，在實際應用中參考源數目并不能保證；文獻[12]指出差分校正(Differential calibration, DC)算法可以有效消除時間同步誤差，但其對星歷誤差的校正效果嚴重依賴于參考源距離輻射源的遠近，當參考源距輻射源較遠時，DC算法對星歷誤差的校正效果較差。

鑒于上述有源校正算法的不足，本文提出了一種基于正交投影的兩步迭代有源校正算法，首先通過正交投影消除觀測方程中的時間同步誤差，然后在校正星歷誤差時，為了避免待估計參數過多和非線性估計的問題，引入一個與輻射源位置和星歷誤差有關的中間變量，通過對該中間變量的最優估計消除了星歷誤差對定位精度的影響，最后利用中間變量求解出目標輻射源的位置。此外，本文還推導了所提算法的理論性能和相應的CRLB，最后通過計算機仿真校驗證明了本文算法的有效性。

1　問題建模

考慮靜止于地球表面的輻射源，其所在位置的經度和緯度分別為θ和φ，記α=[θ,φ]T。假定地球模型為球模型，則輻射源在地心坐標系下的位置矢量可表示為：

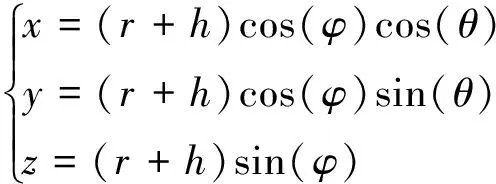
(1)

式中：h為已知的輻射源高程。

三顆衛星星歷的觀測值為

(2)

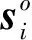
記c為電磁波傳播速度，ti1為第i顆衛星相對于第1顆衛星接收到輻射源信號的TDOA觀測值，則對應的到達距離差(Range difference of arrival, RDOA)為ri1=c·ti1。在時差定位中TDOA與RDOA是等效的，為便于表示，下文中均采用RDOA形式。輻射源信號的RDOA觀測值為

(3)

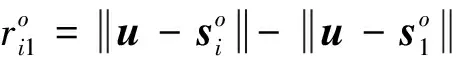
為了校正星歷誤差和時間同步誤差，引入M個位置精確已知的參考源，記第j個參考源的位置矢量為cj。若三顆衛星同時或在較短時間間隔內接收輻射源和參考源信號，則可認為輻射源信號和參考源信號對應的星歷誤差和時間同步誤差是相同的，因此參考源信號的RDOA觀測值為：

(4)

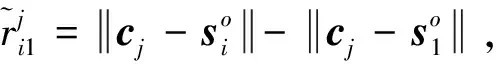
將式(3)和式(4)改寫成矩陣形式：

m=mo+Hτ+n

(5)

式中：

(6)

式中：?表示Kronecker積，1(M+1)×1是元素全為1的列矢量，I2是2維單位矩陣。考慮到三星時差定位系統中星間距一般較大，信號被大范圍內分布的衛星接收終端截獲，這使得信號在傳播過程中引入的噪聲之間是獨立的；此外，由于處在不同環境的接收終端物理器件的差異性，使得接收環節引入的噪聲也是獨立的；由中心極限定理可知，多種獨立噪聲的疊加可近似建模為高斯白噪聲，因此假定n為零均值、協方差矩陣為Qr的高斯白噪聲。

2　輻射源位置估計的CRLB

由于存在地球球面方程的約束，無法直接用CRLB理論求解輻射源位置，又考慮到式(1)中輻射源經緯度α與輻射源位置矢量u的轉換關系，兩者的CRLB存在如下關系[13]：

(7)

式中：C(u)為輻射源位置估計的CRLB，C(α)為輻射源經緯度估計的CRLB，

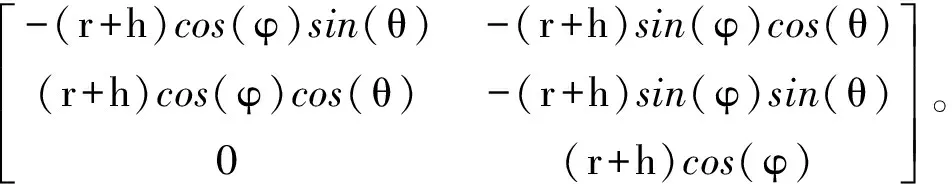
因此，可以將地球球面方程約束下的C(u)的求解問題轉化為求解C(α)。

記x=[mT,sT]T,ψ=[αT,soT,τT]T，則式(5)所示的觀測模型的對數似然函數為：

(8)

關于未知參數ψ的Fisher信息矩陣可分塊表示為：

(9)

式中：

(10)

對式(9)求逆，其左上2×2子矩陣即為C(α)，由矩陣分塊求逆定理可得：

(11)

將式(10)代入式(7)即可得到C(u)，為了便于對比，下面給出僅存在星歷誤差和觀測噪聲情況下輻射源位置估計的CRLB[12]：

C(α)τ=0=(X-YZ-1YT)-1

(12)

對比可以看出，存在參考源時，時間同步誤差的存在會影響輻射源位置估計的CRLB，但C(u)的表達式中不含有τ，這說明時間同步誤差的大小并不影響輻射源位置估計的CRLB。

3　算法原理

為消除星歷誤差和時間同步誤差對定位精度的影響，本文提出一種基于正交投影的兩步迭代校正算法，具體原理如下：

步驟1：首先構造如下正交投影矩陣：

PH=I2(M+1)-H(HTH)-1HT

(13)

對式(5)兩邊左乘PH可得：

PHm=PHmo+PHn

(14)

可以看出，利用H的正交投影PH就可以消除式(5)所示定位模型中的時間同步誤差項。

為進一步消除星歷誤差對定位精度的影響，將mo在s處一階Taylor展開，并忽略高階項可得：

(15)

式中：

(16)

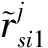
(17)

將式(15)和式(17)代入式(14)并整理可得：

(18)

式(18)可簡記為：

h=Grs+np

(19)

考慮到直接利用式(19)估計輻射源位置需要求解非線性方程，不易求解，因此本文首先估計中間變量rs，然后利用rs求解輻射源位置。等效噪聲np的協方差矩陣為：

(20)

由于正交投影矩陣PH不滿秩，因此Qp亦不滿秩，即等效噪聲np是相關的。為了得到rs的最優估計，首先對Qp奇異值分解：

Qp=UΣUT

(21)

式中：

(22)

U

(23)

ΣR為非零奇異值組成的對角矩陣，U為特征矢量矩陣，UR和UH分別為非零奇異值和零奇異值對應的特征矢量組成的矩陣，且

(24)

因此，URnp為零均值、協方差矩陣為ΣR的高斯白噪聲；UHnp為零均值、協方差矩陣為0的高斯白噪聲，這等價于UHnP=0。在式(20)兩邊同時左乘UT，由UR和UH的正交性可得下式：

(25)

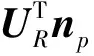
(26)

對代價函數Q進行如下化簡：

(h-Grs)TΓ(h-Grs)

(27)

將式(27)代入式(26)，并對式(26)采用Lagrange乘子法：

L

(28)

分別對rs和λ求導并置零可得：

(29)

將式(29)寫成矩陣形式：

(30)

求解式(30)可得：

(31)

步驟2：下面利用rs求解輻射源位置，由定義可知rs等效于真實星歷為s時衛星接收到輻射源信號的RDOA，因此將中間變量rs和衛星星歷觀測值s代入Ho和Chan提出的三星時差定位算法中[2]，即可求解出輻射源位置，具體定位算法本文不再贅述。

需要指出的是：步驟1中求解rs需要已知Qp，由定義可知Qp的值與輻射源的位置有關，而輻射源位置是未知的，為解決這個問題，可先初始化Qp=Qr，即忽略星歷誤差的先驗信息求解出rs，進而得到輻射源位置的初始估計；再將輻射源位置的初始估計代入式(20)得到Qp的估計，重復步驟1和步驟2，直至輻射源位置估計收斂。由于本文所提的算法是閉式解，收斂速度很快，一般5次以內迭代即可收斂。

4　性能分析

首先依據式(31)給出rs的估計可以得到其估計協方差矩陣為：

(32)

再將式(22)～(23)代入式(21)可得：

(33)

進一步有：

(34)

將式(34)代入式(32)可得：

(35)

由協方差矩陣矢量變換公式[13]可得：

(36)

式中：(·)-T表示對矩陣求逆并轉置。再依據α與u的轉換關系可得：

(37)

將式(35)～(36)代入式(37)可得輻射源位置估計的協方差矩陣為：

(38)

5　仿真校驗

下面利用計算機仿真來校驗本文所提算法的有效性，采用均方根誤差和估計偏差來衡量算法性能，其定義分別如下：

(39)

為表明本文算法的有效性，將本文算法的蒙特卡洛仿真結果與本文算法的理論性能、CRLB以及差分校正算法進行比較。假定輻射源、參考源和三顆衛星的位置如表1所示；輻射源和參考源的觀測噪聲協方差矩陣Qr為對角陣，TDOA觀測噪聲的標準差σt=100 ns，時間同步誤差τi1在100 ns～300 ns區間內隨機選取；星歷誤差協方差矩陣Qs為對角矩陣，星歷誤差的標準差σs=1000 m。除非重新聲明，否則仿真場景均采用上述參數。

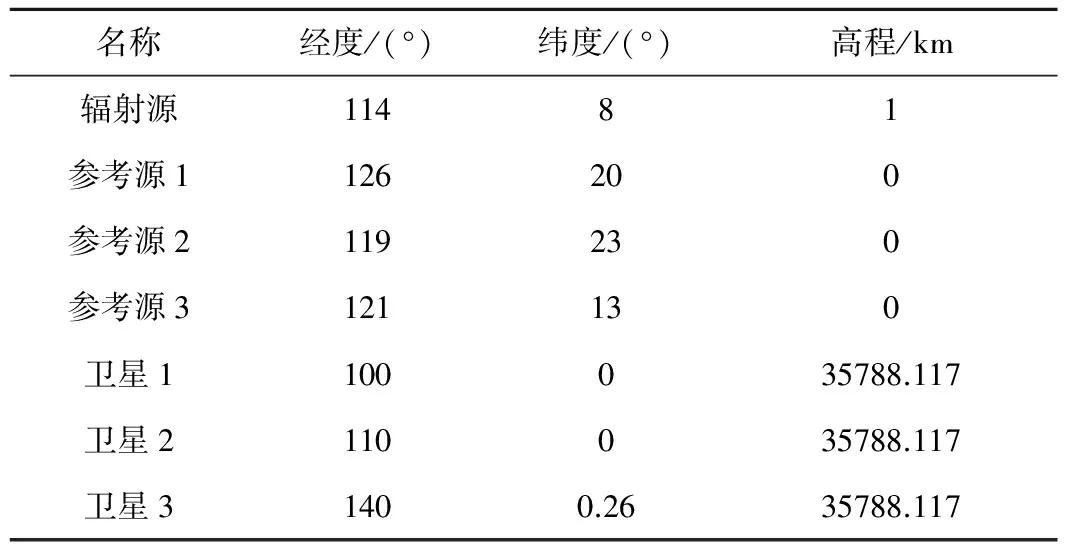
表1　仿真場景Table 1　Simulation scene

仿真1：單參考源(參考源1)條件下本文算法的性能仿真。圖1和圖2分別為本文算法定位誤差隨TDOA觀測噪聲和星歷誤差的變化曲線，從圖1～2可以看出：本文算法定位精度的蒙特卡洛仿真值與理論性能基本吻合，且定位精度可以達到CRLB；在單參考源條件下，差分校正算法也可以達到CRLB，本文算法與差分校正是等效的；此外，本文算法的估計偏差接近于零，相比均方根誤差，估計偏差可以忽略，即本文算法得到的輻射源位置估計是無偏的。

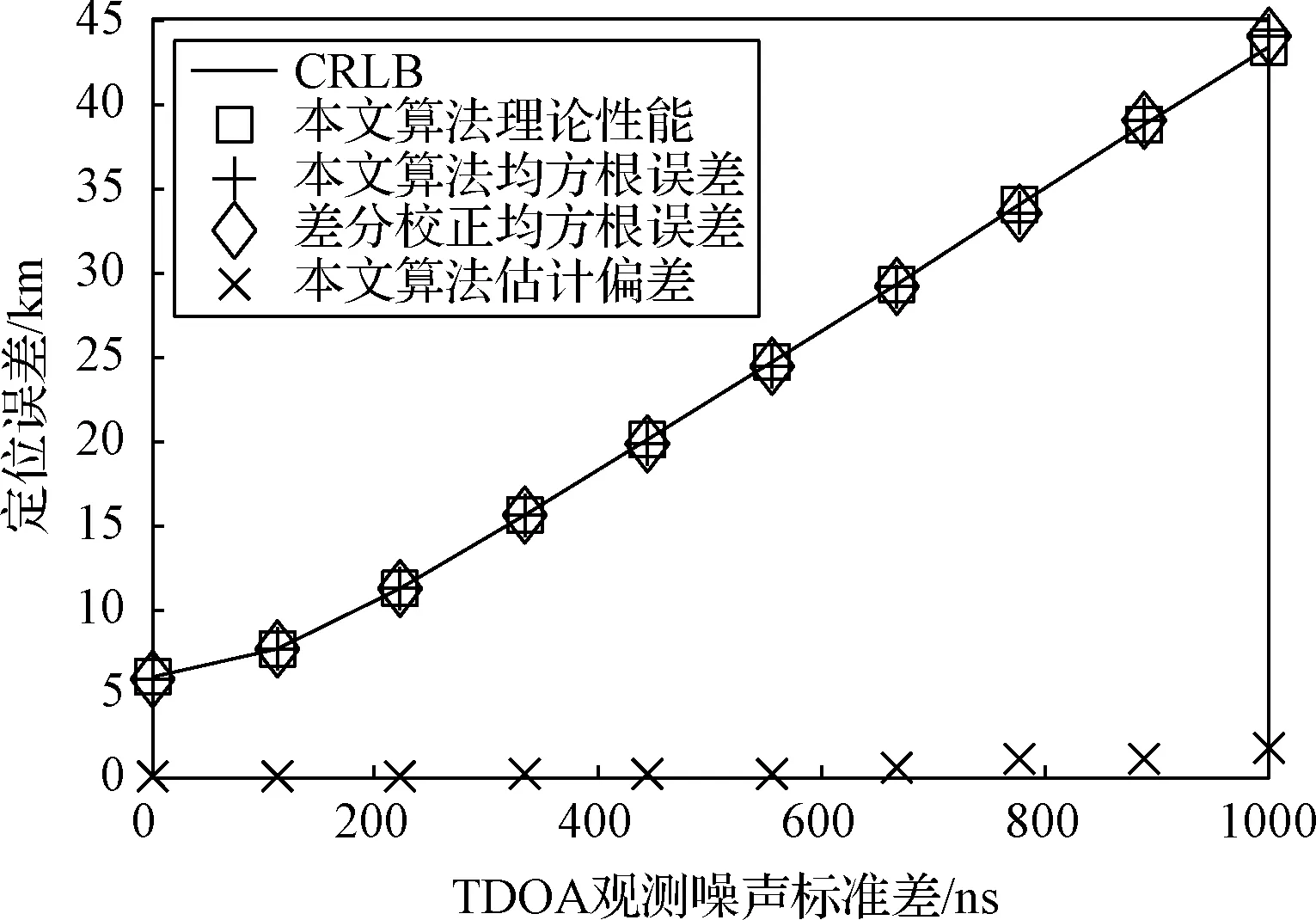
圖1　定位誤差隨TDOA噪聲標準差變化曲線(單參考源)Fig.1　Curves of location error changing with TDOA noise standard deviation using 1 calibration source

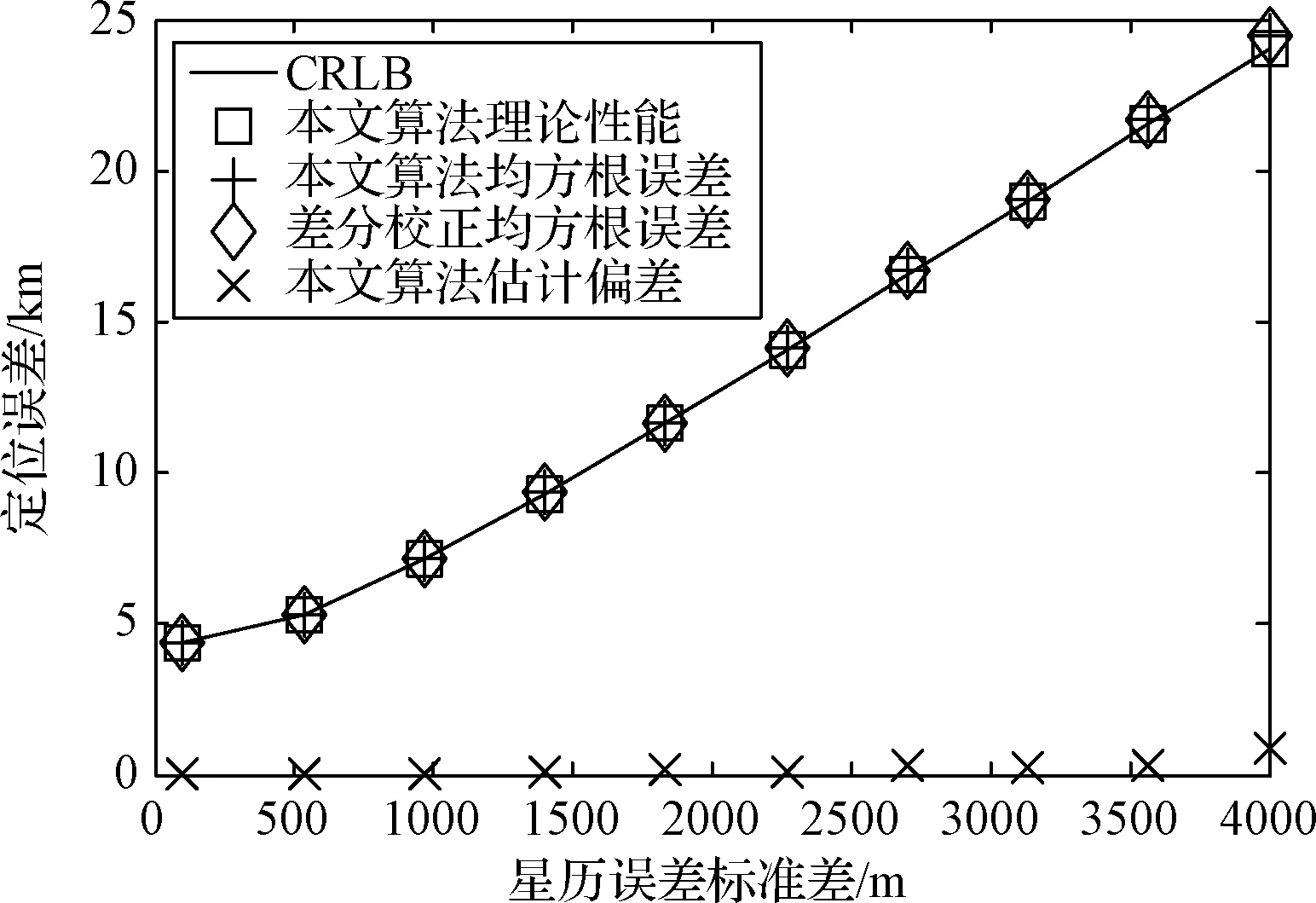
圖2　定位誤差隨星歷誤差標準差變化曲線(單參考源)Fig.2　Curves of location error changing with satellite position error standard deviation using 1 calibration source

仿真2：3參考源(參考源1～3)條件下本文算法的性能仿真。圖3是本文算法定位誤差隨TDOA觀測噪聲變化情況，從圖3可以看出，本文算法和差分校正算法的定位誤差均隨著TDOA觀測噪聲正比例增加，但由于差分校正算法沒有考慮對星歷誤差的校正，本文算法的定位精度要高于差分校正。圖4是本文算法定位誤差隨星歷誤差的變化情況，從圖4可以看出：差分校正算法對星歷誤差十分敏感，其定位誤差幾乎隨星歷誤差線性增加，而本文算法的定位性能仿真值與理論性能均可以達到CRLB；當星歷誤差標準差小于2000 m時，與星歷誤差相比TDOA觀測噪聲對定位誤差的影響無法被忽略，使得本文算法無法完全校正星歷誤差，從而出現了定位誤差隨星歷誤差的增加而增加的現象；而當星歷誤差標準差大于2000 m時，TDOA觀測噪聲對定位誤差的影響可以被忽略，此時本文算法定位誤差幾乎已不隨星歷誤差的增加而變化，此外，輻射源位置估計也是無偏的，這說明3參考源條件下，本文算法可以完全校正星歷誤差和時間同步誤差對定位精度的影響。

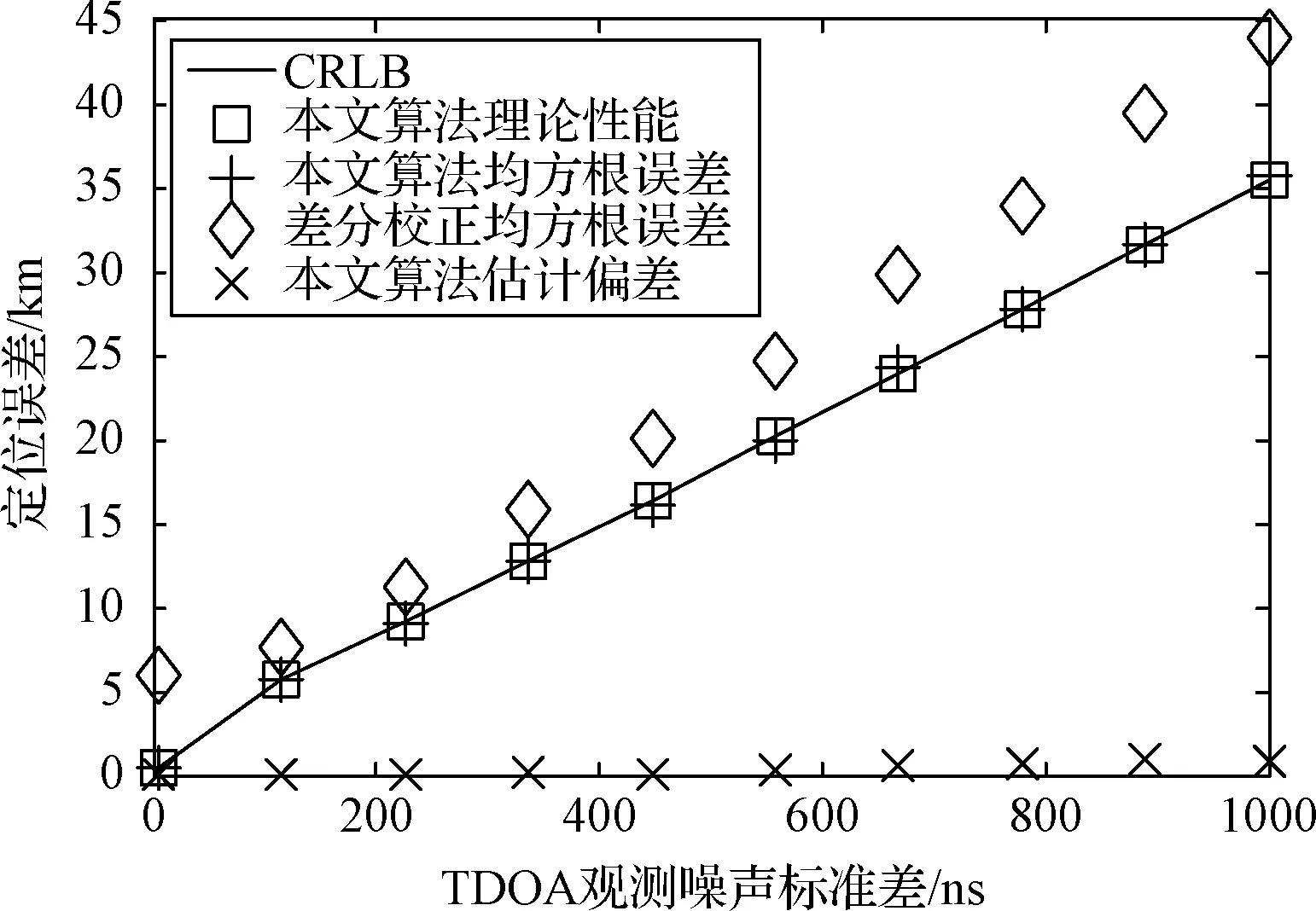
圖3　定位誤差隨TDOA噪聲標準差變化曲線(3參考源)Fig.3　Curves of location error changing with TDOA noise standard deviation using 3 calibration sources

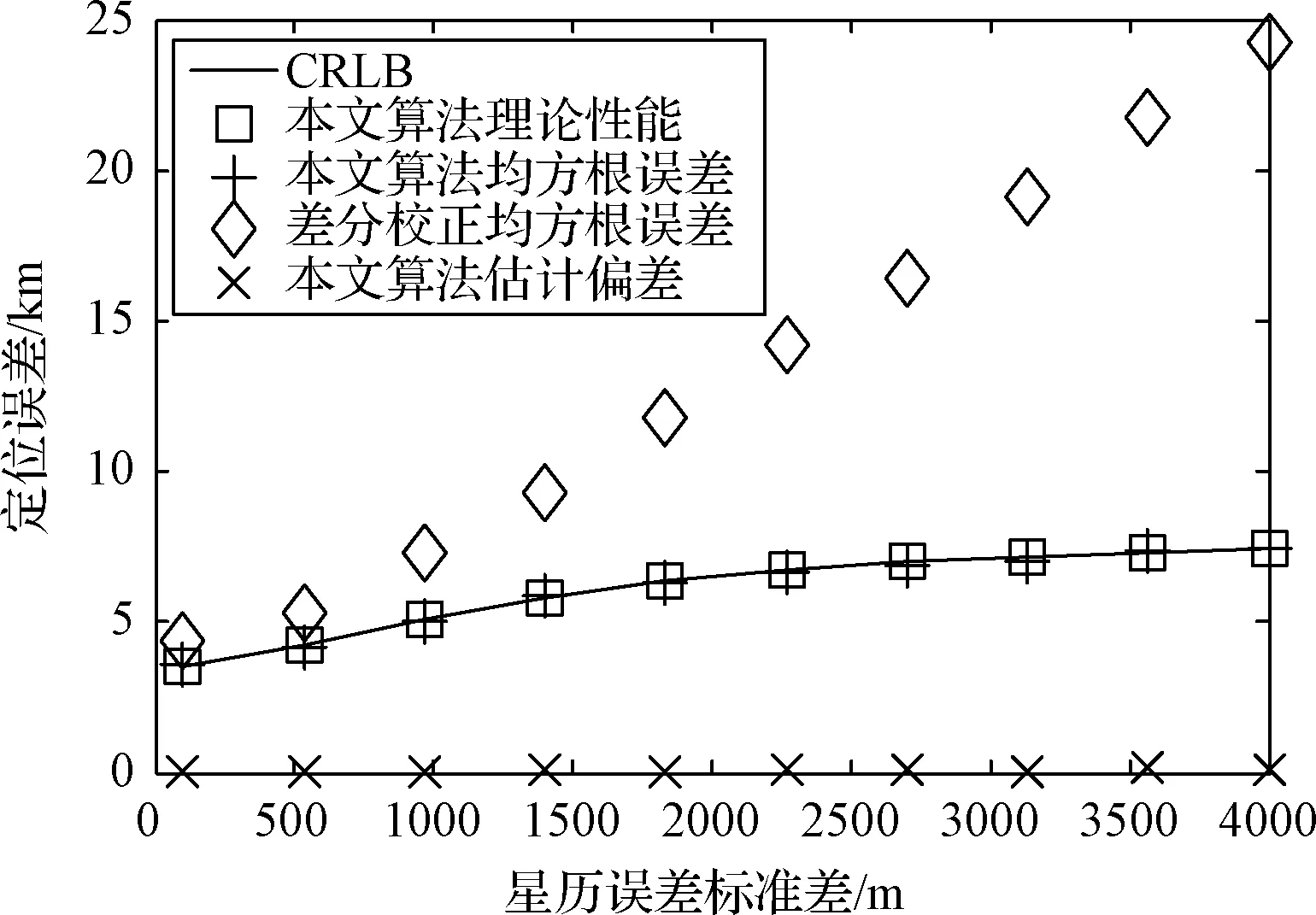
圖4　定位誤差隨星歷誤差標準差變化曲線(3參考源)Fig.4　Curves of location error changing with satellite position error standard deviation using 3 calibration sources

6　結　論

本文針對三星時差定位系統中星歷誤差和時間同步誤差的校正問題，提出一種基于正交投影的兩步迭代有源校正算法，計算機仿真結果表明，無論是單參考源還是多參考源條件本文算法的仿真值和理論性能均可以達到CRLB，且在三參考源條件下，可以完全消除星歷誤差和時間同步誤差對定位精度的影響。本文算法適用于任意數目參考源條件下的有源校正，并且是閉式解，收斂速度快，具有較好普適性和應用價值。

[1]Ha T T, Robertson R C. Geostationary satellite navigation systems. [J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, 23(2): 247-254.

[2]Ho K C, Chan Y T. Geolocation of a known altitude object from TDOA and FDOA measurements [J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 770-783.

[3]Wang D, Wei S, Wu Y. A performance analysis of multi-satellite joint geolocation [J]. Front. Inform. Technol. Electron. Eng., 2016,17(12): 1360-1387.

[4]Wang Y, Ho K C. TDOA source localization in the presence of synchronization clock bias and sensor position errors [J]. IEEE Transactions on Signal Processing, 2013, 61(18): 4532-4544.

[5]Ma Z H, Ho K C. A study on the effects of sensor position error and the placement of calibration emitter for source localization [J]. IEEE Transactions on Wireless Communications, 2014, 13(10): 5440-5452.

[6]Li J Z, Pang H W, Guo F C, et al. Localization of multiple disjoint sources with prior knowledge on source locations in the presence of sensor location errors [J]. Digital Signal Processing, 2015(40): 181-197.

[7]Yang L, Ho K C. Alleviating sensor position error in source localization using calibration emitters at inaccurate locations [J]. IEEE Transactions on Signal Processing, 2010, 58(1): 67-83.

[8]夏暢雄，葉尚福，王俊輝. 衛星干擾源定位系統中衛星星歷星歷校正技術 [J]. 宇航學報, 2008, 29(3): 860-863. [Xia Chang-xiong, Ye Shang-fu, Wang Jun-hui. Ephemeris determination in satellite interference location system [J]. Journal of Astronautics, 2008, 29(3): 860-863.]

[9]王鼎. 觀測站位置狀態擾動下Taylor級數迭代定位方法及性能分析 [J]. 宇航學報, 2013, 34(12): 1634-1643. [Wang Ding. The Taylor-series location and its performance analysis with erroneous observer positions [J]. Journal of Astronautics, 2013, 34(12): 1634-1643.]

[10]Liu C, Yang L, Mihaylova L. Dual-satellite source geolocation with time and frequency offsets and satellite location errors [C]. The 20th International Conference on Information Fusion, Xi’an, China, July 10-13, 2017.

[11]王瑩桂，李騰，陳振林，等. 三星時差定位系統的四站標定方法 [J]. 宇航學報, 2010, 31(5): 1352-1356. [Wang Ying-gui, Li Teng, Chen Zhen-lin, et al. Tri-satellite TDOA location system-based four station calibration technique [J]. Journal of Astronautics, 2010, 31(5): 1352-1356.]

[12]Ho K C, Yang L. On the use on of a calibration emitter for source localization in the presence of sensor position uncertainty [J]. IEEE Transactions on Signal Processing, 2008, 56(12): 5758-5772.

[13]Steven M K. 統計信號處理基礎 [M]. 羅鵬飛，張文明，劉忠，等譯. 北京：電子工業出版社，2011.