一種基于改進SIFT算法的軌道板圖像匹配方法*

張護望,林　滸,王詩宇,鄭廖默，馮　斌

(1.中國科學院大學，北京　100049；2.高檔數控國家工程研究中心，沈陽　110168； 3.沈陽高精數控智能技術股份有限公司，沈陽　110168)

0　引言

圖像拼接工作就是多幅圖像中檢測出部分相同興趣區域，進而使其實現無縫拼接，進而得到一種全視角的完整圖像。圖像拼接現已普遍應用于工業移動機器人，醫學，軍事，機器視覺等[1-4]領域。圖像拼接技術作為計算機視覺和圖像處理研究的熱點，吸引了很多國內外的學者和科技巨頭公司對其進行大量研究和投資。

在計算機視覺，圖像處理，三維重建，其中最重要的技術就是實現圖像高精度配準[5]，算法大體分為：基于區域的匹配算法基于特征的匹配算法。基于特征的算法，主要工作就是依據圖像的特征點向量來計算圖像之間的相似性關系，來判斷圖像匹配的興趣區域。相比于區域匹配具有較低的計算復雜性和較高的穩定性。所以在圖像配準技術中非常重要的地位。文獻[6]提出了一種使用KLT跟蹤技術, 精確確定各特征角點的位置,從而得到兩幅圖像之間精確的變換矩陣，角點的定義直接影響匹配結果；文獻[7]采用SIFT特征點進行圖像拼接；文獻[8]采用PCA降維的方法，使用主元分析，使得128維向量降維到了36位向量，降低了SIFT算法的計算復雜度，但丟失了原始圖像的部分信息，可能會影響結果。Smith等[9]提出了SUSAN算法，它不依賴于圖像的導數，具備較強的抗噪聲能力，但運算速度比較慢。Bay[9]提出了一種更快的加速算子SURF來替代SIFT算子。為了加快速度，SURF算子采用盒子濾波來替代高斯濾波。Moravec提出了使用灰度方差的技術檢測角點，具備最小灰度變化的極大值點。研究者根據實際情況，對上述算法進行改進外，還根據存在的問題提出了很多的算法。國內的肖秩軍等[10]提出了基于B樣條模型的曲線特征點檢測方法，樣條函數的選擇影響匹配效果。文獻[11]首先對圖像利用SIFT算法進行特征提取和與匹配，使用 RANSAC算法剔除不穩定的匹配結果，并精確計算圖像間的變換參數。文獻[12]提出了提取顯著區域特征并生成SIFT特征向量，從而計算相似性實現圖像匹配，注重顯著區域的特征選擇。文獻[13]采用非對稱特征搜索方式，實現方向性的特征匹配。都取得了很好的匹配效果，結果更加穩定。

本文提出了一種采用96維特征描述子，降低了128維向量的復雜度，盡可能的保留圖像信息。并采用皮爾遜相關性評分進行配準分析的圖像匹配算法，實驗表明，文中算法可以得到較好的匹配結果，具有較高的穩定性。

1　SIFT原理

SIFT算法對于尺度變化，亮度變化，位置變化，視覺角度問題都有很高的魯棒性。本文的應用場景對光照，拍攝角度要有較強的抗噪性，SIFT可以克服這些問題。SIFT主要思路是：首先要有圖像的尺度空間表示，進而檢測該圖像不同尺度空間極值點，標記特征點的主方向，最后生成特征點描述子。

1.1　尺度空間極值點檢測

首先應用不同尺度的高斯濾波函數G(x,y,σ)對原始圖像I(x,y)作卷積運算，進行尺度變換。設(x,y)是原始圖像I的函數表示，σ是尺度因子，則圖像尺度空間L定義為：

L(x,y,σ)=G(x,y,σ)I(x,y)

(1)

其中，高斯函數為：

(2)

對輸入圖像進行降采樣構建輸入圖像的高斯金字塔，相減得到高斯差分(DOG) 金字塔。公式(3)所示：

D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))×I(x,y)=
L(x,y,kσ)-L(x,y,kσ)

(3)

其中，參數k為相鄰的圖像之間的尺度因子比例。將相鄰3層DOG圖像的極值點確定為關鍵點。

1.2　特征點方向計算

前面檢測的極值點中，會存在一些低對比度、不穩定的誤匹配極值點。為了剔除這些不穩定點、提高匹配的穩定性、增強抗干擾能力，SIFT算法中采取曲線擬合的方法剔除低對比度的特征點，而且使用Hessian矩陣剔除不穩定的誤匹配點。已經得到了每幅圖像中的極值點，每個極值點都包含其尺度信息，利用以極值點所在鄰域中像素的梯度方向統計分布為依據，為每個極值點指定主方向，旋轉坐標軸，使算子具備旋轉不變形。式(4)和式(5)中：

m(x,y)=

(4)

θ(x,y)=αtan2((L(x,y+1)-L(x,y-1))/
(L(x+1,y)-L(x-1,y)))

(5)

其中，L如公式(3)所示，尺度因子σ為每個極值點所在的尺度。

1.3　生成特征點描述子

為了保證旋轉不變性，首先將關鍵點的方向指定為坐標軸方向。對于每一個特征點，在其相應的尺度空間，以每個特征點為中心所在的16×16大小的鄰域窗口，采用高斯下降函數降低遠離關鍵點中心的像素的權重。每個特征點將會得到4×4×8=128維的描述子。如圖1所示，圖中描述了一個關鍵點由4個種子點構成。

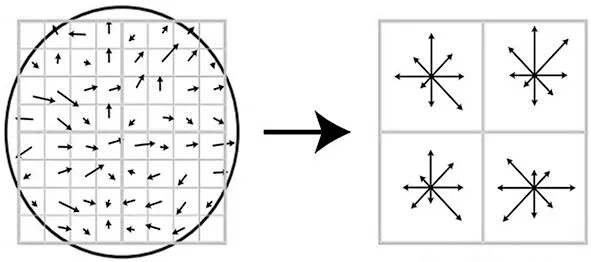
圖像梯度　　　　　　　關鍵點描述圖1　描述子構建

1.4　特征點匹配

得到兩幅圖像的SIFT向量，使用特征向量的歐式距離判斷兩幅圖像中關鍵點的相似性。采用k-d數算法，提高了關鍵點特征向量的匹配速度。并且利用RANSAC算法對匹配結果進行篩選，剔除誤匹配點。最終得到關鍵點的匹配結果。對于兩幅圖像，當達到一定的相似度時，就認為兩幅圖像有同一個興趣區域。

2　改進的SIFT算法

數字圖像在獲取和傳輸過程中容易受到噪聲污染和數據缺失等問題，但是圖像處理過程中首要工作就是要去噪，噪聲給后續的圖像匹配和拼接等工作帶來很多不可避免的問題。消除噪聲是圖像處理中不可或缺的一部分。主要就是圖像預處理階段進行圖像濾波和平滑處理。所以對原始圖像必須進行去噪處理和數據還原等操作，促使后期處理盡可能達到最優。傳統的圖像去噪算法有均值濾波，限幅濾波，高斯濾波，中值濾波等。本文采用雙邊濾波器來實現，盡可能的保留原圖像信息內容。下面簡單介紹雙邊濾波的相關內容。

2.1　雙邊濾波器

雙邊濾波(Bilateral filter)保住了邊緣信息，去除了噪聲，是一種非線性的圖像濾波方式，是圖像空間的鄰近度和像素間相似度的一種調和方法，并且還結合了空域信息和灰度相似性。濾波器函數中由兩部分組成。一部分由歐式幾何距離來選取濾波器系數。另一部分是由像素間差值選取濾波器系數。

(6)

權重系數w(i,j,k,l) 取決于定義域核(公式(7))和值域核(公式(8))的乘積。

(7)

(8)

(9)

公式(9)中主要求取空間域與值域的差異。對原始圖像進行預處理，本文使用雙邊濾波器，能夠保存原始圖像的邊緣信息，最大程度的保留了原始信息，有利于后續操作。

2.2　內切降維

構建DOG，然而經過DOG檢測得到的特征點，存在一些不穩定的特征點。使用擬和三維二次函數，從而確定關鍵點的位置信息和尺度信息，并且剔除低對比度的關鍵點和不穩定的邊緣響應點，以提高匹配穩定性、增強抗噪聲的能力。得到特征集之后，需要給每個特征點賦值一個128維方向參數。如圖2所示，傳統SIF算法得到的是128維向量，在原算法的基礎上，本文采用的是16×16窗口的內切圓，只保留圖中紅色標記的小窗口中的種子點，去除了窗口的4角的種子點，共有12個種子點，每個種子點統計8個方向值。最后得到12×8=96維向量。為了進一步的降低光照變化對處理結果的影響，可以對特征向量進行歸一化處理，則可以這樣，96維向量中充分保留了特征點周圍的像素信息，一定程度上降低了遠離中心點像素的計算復雜度。對后續進行特征點匹配選取做準備。

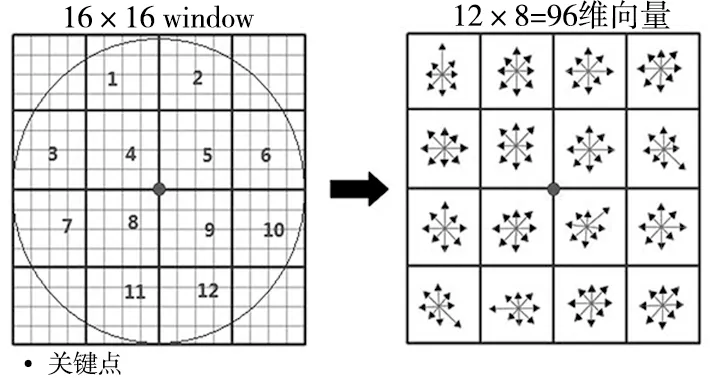
圖2　降維處理示意

2.3　相關系數評判匹配

本文經過降維處理之后，得到了每個特征點各自的96維向量。采用特征向量的皮爾遜相關系數相似度作為兩幅圖像中特征點的相似度判定方式。取圖像1中的某個特征點，并找出其與圖像2中皮爾遜相關系數大于閾值ratio的關鍵點，則接受這一對匹配點。皮爾遜相關系數公式(10)中，

(10)

公式中，R(X,Y)代表的意義是向量X和Y所代表的特征向量線性相關的強弱程度，其中包含-1≤R(X,Y)≤1，若R(X,Y)=0,表示兩個特征向量非線性相關，若R(X,Y)<0表示兩個特征向量負相關，若R(X,Y)>0則表示兩個特征向量正相關，然而R(X,Y)的絕對值越大表明兩個特征向量相關性越強。一般會對計算之后的相關系數取絕對值。我們只考慮是否相關就行。只要滿足一定條件下的強相關條件就表示兩個特征向量相關。此處表明接收特征點匹配。

本文中通過計算相關系數，得到相關系數矩陣，每個特征點都會有一個和其他特征點相關的評判系數。對每一個特征點相關系數進行降序排序，選取相關性最大的特征點，并且當前相關系數大于閾值，此特征點作為當前特征點的匹配結果，則接受這對特征匹配點。

3　實驗結果與分析

以上步驟完成匹配后，得到的是兩幅圖像之間的特征點接收匹配的結果集合，我們根據最初匹配結果集選用RANSAC方法迭代尋找一個最佳單應矩陣，包含盡可能多的數據點。這樣可以去除一些誤匹配點，本文選取無砟軌道板部分圖像，如圖3是左圖經過雙邊濾波器處理的結果，圖4為右圖經過雙邊濾波器處理的結果。圖5和圖6可以看出選取合適的閾值很重要，相關系數較小的閾值可能會存在誤匹配情況，較大閾值可能存在丟失一部分正確的匹配結果，經過試驗之后選取閾值為0.6可以看出結果理想。利用本文算法得到的匹配結果一致。提高了匹配精度和穩定性。

圖3　左圖雙邊濾波器處理結果

圖4　右圖經過雙邊濾波器處理結果

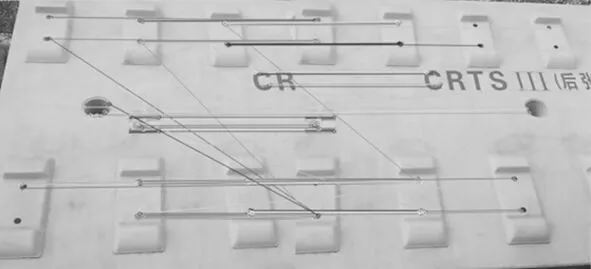
圖5　相關系數閾值為0.5

圖6　相關系數為0.6

實驗結果證明，改進之后的算法，當閾值為0.5的時候，匹配結果會出現一些誤匹配點，當閾值為0.6時，匹配結果沒有出現誤匹配特征點。所以改進之后的算法，在保證特征點個數的情況下，也滿足特征匹配的要求，也經過了多次試驗，匹配結果穩定。

4　結束語

本文首先通過雙邊濾波器處理輸入圖像，再進行特征點檢測操作，利用內切圈去除了遠離中心點的像素值，減少了計算復雜度，得到特征點向量，最后通過皮爾遜相關性評價是否接受匹配。此方法減少了特征點的錯誤匹配，通過降維的方法處理特征向量提高了整個系統的處理速度。進行匹配時對相關系數進行排序，選取相關性最大的作為新的特征匹配點。用RANSAC迭代的方法得到最優的匹配結果集。本文中采用的96維向量不免會丟失一些圖像信息，實驗結果表明，在相關系數閾值為0.6時，匹配結果不存在誤匹配的現象，滿足軌道板圖像匹配的要求。

[參考文獻]

[1] Chen Y, Xu M, Liu HL, et al. An improved image mosaic based on Canny edge and an 18-dimensional descriptor[J]. Optik-International Journal for Light and Electron Optics 2014,125(17):4745-4750.

[2] Wu ZG, Wang MJ, Wang YQ. Image mosaic technique based on the information of edge [J]. International Conference on Digital Manufacturing & AutomationMauceri, 2012:482-484.

[3] Zhang K, Li XZ, Zhang J. A Robust Point-Matching Algorithm for Remote Sensing Image Registration[J]. Geoscience & Remote Sensing Letters IEEE,2013,11(2):469-473.

[4] 曹世翔, 江潔, 張廣軍, 等. 邊緣特征點的多分辨率圖像拼接[J]. 計算機研究與發展,2011,48(9):1788-1793.

[5] 孟龍暉. 一種大壁虎腦圖譜三維重建的新方法及實現[D].南京:南京航空航天大學,2011.

[6] 胡社教, 葛西旺, 陳宗海. 基于角點特征的KLT跟蹤全景圖像拼接算法[J]. 系統仿真學報,2007,19(8):1742-1753.

[7] 高華. 基于SIFT圖像拼接技術研究[D]. 重慶:重慶交通大學,2012.

[8] Yan K, Sukthankar R. PCA-SIFT: a more distinctive representation for local image descriptors[J]. 2004,2(2):506-513.

[9] Bay H, Ess A, Tuytelaars T, et al. Speeded-Up Robust Features (SURF)[J]. Computer Vision & Image Understanding 2008,110(3):346-359.

[10] 肖軼軍, 丁明躍. 基于B樣條模型的曲線特征點檢測法[J]. 數據采集與處理,2000,15(4):422-425.

[11] 常青. 基于SIFT和RANSAC的特征圖像匹配方法[J]. 華東理工大學學報:自然科學版,2012,38(6):97-101.

[12] 尹春霞, 徐德, 李成榮, 等. 基于顯著圖的SIFT特征檢測與匹配[J]. 計算機工程,2012,38(16):189-191.

[13] 杜振龍, 楊凡, 李曉麗, 等. 利用SIFT特征的非對稱匹配圖像拼接盲檢測[J]. 中國圖象圖形學報,2013,18(4):442-449.

(編輯李秀敏)