與整數有序分拆的分部量1相關的一些恒等式
郭 育 紅
(河西學院數學與統計學院,甘肅 張掖 734000)
1 預備知識
在經典的分拆理論中,MacMahon[1]給出了正整數有序分拆的定義,從而正整數n被表示成了若干正整數的有序和,其中每一項被稱為該分拆的分部量.例如,可將4有序分拆成4,3+1,1+3,2+2,2+1+1,1+2+1,1+1+2,1+1+1+1;而無序分拆有4,3+1,2+2,2+1+1,1+1+1+1.

圖1 14的有序分拆(6,3,1,2,2)的zig-zag圖
有序分拆的zig-zag圖:將有序分拆的每個分部量λ按照順序用含有λ個點的行表示,同時要求下一行的第一個點與上一行的最后一個點對齊.分拆14的有序分拆(6,3,1,2,2)的zig-zag圖如圖1所示.
利用有序分拆的zig-zag圖可得到有序分拆的共軛分拆,即將zig-zag圖從左到右按照列讀得到的分拆就是原分拆的共軛分拆.例如,圖1按列讀產生的有序分拆(1,1,1,1,1,2,1,3,2,1)就是(6,3,1,2,2)的共軛分拆,它們互為共軛.Munagi[2-3]介紹了包括zig-zag圖在內的五種有序分拆的共軛分拆的求法.
分拆恒等式的研究一直是分拆理論中有趣而內容豐富的一個課題,近年來涌現許多研究結果.[4-10]2015年,Munagi和Sellers[11]指出:如果正整數的一個有序分拆中分部量λ連續出現j次,則稱分部量λ出現Inplacej次.該文還給出了關于有序分拆的若干Inplace恒等式.
定理1.1[11]設n≥1,正整數n的偶分部量出現Inplace偶數次的有序分拆數等于正整數n不含分部量≡2(mod 4)的有序分拆數.
定理1.2[11]設n≥1,正整數n的奇分部量出現Inplace偶數次的有序分拆數等于正整數2n的奇分部量有兩種形式的有序分拆數.
文獻[11]將分部量λ有兩種形式表示成:λ,λ*,同時將上述恒等式中分部量做了推廣,得到了更一般的Inplace分拆恒等式.
本文考慮正整數n的分部量1有兩種形式的有序分拆問題,發現正整數n的分部量1有兩種形式的有序分拆數等于第2n+1個Fibonacci數F2n+1.于是結合Fibonacci數與正整數的一些有約束的有序分拆之間的關系,得到了關于正整數n的分部量1有兩種形式的有序分拆數與正整數n的分部量是奇數的有序分拆數,分部量是1或2的有序分拆數,分部量大于1的有序分拆數之間的一些恒等式.
2 主要結果
關于正整數n的分部量1有兩種形式的有序分拆,本文沿用文獻[11]中記號,即用1與1*表示分部量1的兩種形式.
定理2.1設n≥1,正整數n的分部量1有兩種形式的有序分拆數等于2n的不含分部量2k+1,k>0,且分部量1出現Inplace偶數次的有序分拆數.
證明類似于文獻[11]中的證法,對于正整數n的分部量1有兩種形式的有序分拆,作如下變換:將每個大于1的分部量λ變換成2λ,把沒有帶*號的分部量1變換成2,把帶*號的分部量1*變換成(1,1).于是得到了正整數2n的不含大于1的奇分部量,而分部量1出現Inplace偶數次的有序分拆.顯然,上述變換是可逆的,故結論成立.


這里給出該遞推關系的一個組合雙射證明.
證明將n的分部量1有兩種形式的有序分拆和n-2的分部量1有兩種形式的有序分拆分成兩類:
(A)n的有序分拆中右端分部量是1或1*;
(B)n的有序分拆中右端分部量是h,h>1以及n-2的有序分拆.
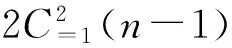


將分部量是1或2的有序分拆稱為1-2有序分拆,分部量是奇數稱為奇有序分拆.
引理2.1[12]正整數n的1-2有序分拆數等于Fn+1.這里Fn是第n個Fibonacci數.
引理2.2[12]正整數n的奇有序分拆數等于Fn.這里Fn是第n個Fibonacci數.
引理2.3[12]正整數n的分部量大于1的有序分拆數等于Fn-1.這里Fn是第n個Fibonacci數.
考慮關于正整數n的分部量1有兩種形式的有序分拆與1-2有序分拆、奇有序分拆、分部量大于1的有序分拆之間的關系,得到下面幾個恒等式.
定理2.3設n≥1,正整數n的分部量1有兩種形式的有序分拆數等于2n的1-2有序分拆數.
證明將n的分部量1有兩種形式的有序分拆分成以下兩類:
(A)n的有序分拆中分部量都是1;
(B)n的有序分拆中分部量至少有一個不是1.
對于(A)類中的任意一個有序分拆,由定理2.1證明中給出的對應關系,可知這類分拆對應著2n的1-2有序分拆中分部量1出現Inplace偶數次的分拆.

定理2.4設n≥1,正整數n的分部量1有兩種形式的有序分拆數等于2n+1的奇有序分拆數.
這里仍給出該恒等式的組合證明.
證明由定理2.3的證明知道,正整數n的分部量1有兩種形式的有序分拆對應著2n的1-2有序分拆.于是,對于2n的任何一個1-2有序分拆,在其右端添上分部量1,然后按照從右向左的順序將1及其左邊的所有2合并成一個新的分部量,便得到2n+1的奇有序分拆.反之亦然.
定理2.5設n≥1,正整數n的分部量1有兩種形式的有序分拆數等于2n+2的分部量>1的有序分拆數.
證明由定理2.3的證明可知,正整數n的分部量1有兩種形式的有序分拆對應著2n的1-2有序分拆.于是對于2n的任何一個1-2有序分拆α,在其左右兩端分別添上分部量1,就得到2n+2的兩端分部量都是1的1-2有序分拆β.下面求分拆β的共軛分拆β′,由于分拆β是左右兩端分部量都是1的1-2有序分拆,故其共軛分拆β′就是分部量大于1的有序分拆.從而得到了2n+2的分部量大于1的有序分拆.反之亦然.
表1給出了當n=3時,正整數n的分部量1有兩種形式的有序分拆與正整數2n的1-2有序分拆、正整數2n+1奇有序分拆、正整數2n+2分部量大于1的有序分拆之間的對應關系.
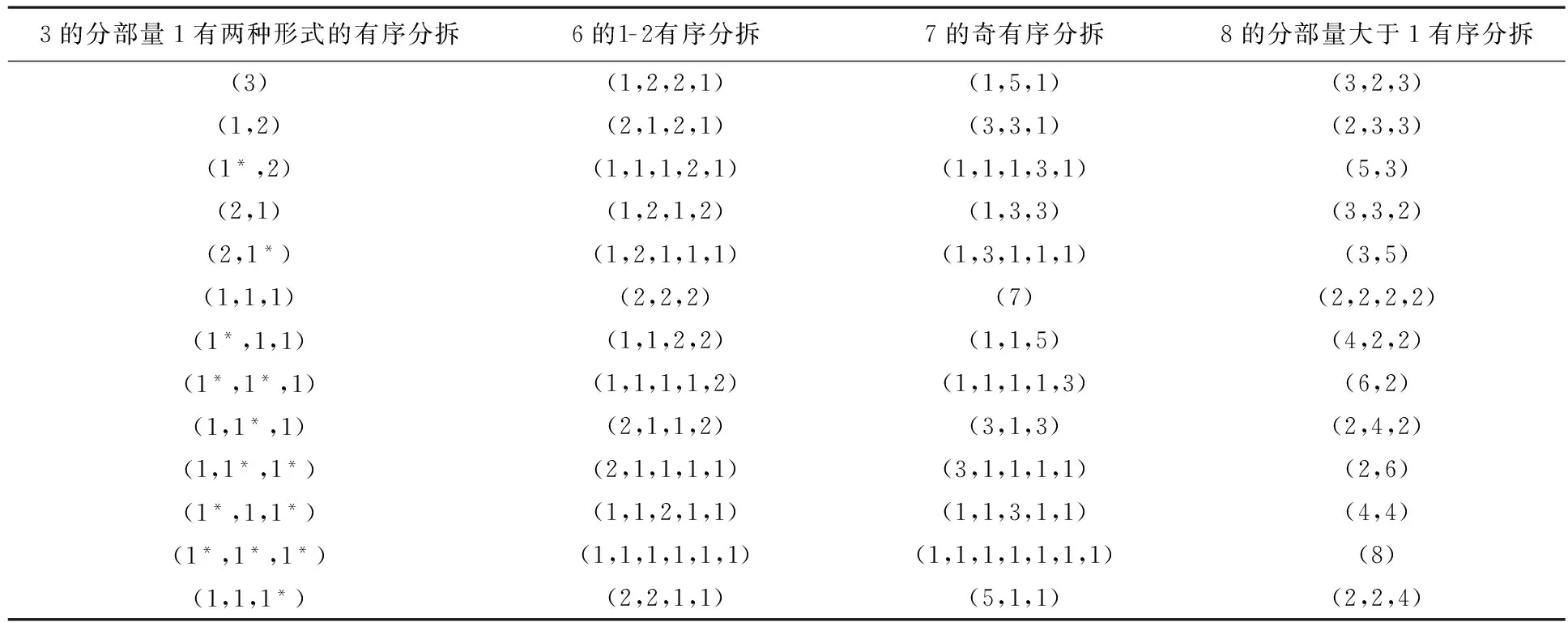
表1 3,6,7,8的各種有序分拆之間的對應關系
由定理2.1,2.3—2.5,自然有下面關于正整數n的分部量1出現Inplace偶數次的有序分拆數與正整數n的1-2有序分拆數、奇有序分拆數、分部量大于1的有序分拆數之間的關系式.
推論2.1設n≥1,正整數n的不含分部量2k+1,k>0,且分部量1出現Inplace偶數次的有序分拆數等于n的1-2有序分拆數.
推論2.2設n≥1,正整數n的不含分部量2k+1,k>0,且分部量1出現Inplace偶數次的有序分拆數等于n+1的奇有序分拆數.
推論2.3設n≥1,正整數n的不含分部量2k+1,k>0,且分部量1出現Inplace偶數次的有序分拆數等于n+2的分部量>1有序分拆數.
下面給出推論2.1的一個例子.
例2.1取n=6,則6的不含大于1的奇分部量,且分部量1出現Inplace偶數次的有序分拆有13個:(6),(4,2),(4,1,1),(2,4),(1,1,4),(2,2,2),(2,2,1,1),(2,1,1,2),(1,1,2,2),(2,1,1,1,1),(1,1,2,1,1),(1,1,1,1,2),(1,1,1,1,1,1).
同樣,6的1-2有序分拆有13個:(1,2,2,1),(1,2,1,2),(1,2,1,1,1),(2,1,2,1),(1,1,1,2,1),(2,2,2),(2,2,1,1),(2,1,1,2),(1,1,2,2),(2,1,1,1,1),(1,1,2,1,1),(1,1,1,1,2),(1,1,1,1,1,1).
[參考文獻]
[1]MACMAHON P A. Combinatory analysis:volumes 1[M].Cambridge:Cambridge University Press,1915:6-32.
[2]MUNAGI A O. Primary classes of compositions of numbers [J].Annales Mathematicae et Informaticae,2013,41:193-204.
[3]MUNAGI A O. Zig-zag graphs and partitions identities of A K Agarwal [J].Annals of Combinatorics,2015,19(3):557-566.
[4]ANDREWS G E,HIRSCHHORN M D,SELLERS J A. Arithmetic properties of partitions with even parts distinct [J].Ramanujan Journal,2010,23:169-181.
[5]CHEN S C. On the number of partitions with distinct even parts [J].Discrete Math,2011,311(12):940-943.
[6]HEUBACH S,MANSOUR T. Combinatorics of compositions and words [M]// Discrete mathematics and its applications.Boca Raton:CRC Press,2010:61-86.
[7]HIRSCHHORN M D,SELLERS J A. Arithmetic properties of partitions with odd parts distinct [J].Ramanujan Journal,2010,22(3):273-284.
[8]MUNAGI A O. Euler-type identities for integer compositions via zig-zag graphs [J].Integers,2012,A62:1-10.
[9]RADU S,SELLERS J A.Congruence properties modulo 5 and 7 for the pod function [J].Int J Number Theory,2011,7(8):2249-2259.
[10]TOH P C. Ramanujan type identities and congruences for partition pairs [J].Discrete Math,2012,312(6):1244-1250.
[11]MUNAG A O,SELLERS J A.Some inplace identities for integer compositions [J].Quaestiones mathematicae,2015,38(4):535-540.
[12]GESSEL I M,LI J. Compositions and Fibonacci identities [J].Journal of Integer Sequences,2013,16(4):1-16.
[13]ANDREWS G E.The theory of partitions [M].Cambridge:Cambridge University Press,1984:3-15.

