帶有分段常數變量的Logistic模型的穩定性和Neimark-Sacker分支
豆中麗,王 瑞
(1.重慶工商大學融智學院,重慶 400055; 2.重慶大學數學科學學院,重慶 401331)
1 預備知識
在生態系統中,具有分段常數變量微分方程模型的穩定性、分支、混沌等動力學行為逐漸受到眾多學者關注.文獻[1]討論了帶有分段常數變量的單種群Logistic模型
(1)
其中t,r,K∈(0,+∞),[t]表示參數t的整數部分.該文討論了模型在正平衡點處的穩定性和分支行為,指出當參數r等于某特殊值時,該模型在正平衡點附近出現混沌現象.文獻[2]討論了一類具有功能反應函數與食餌數量成正比的模型,但捕食者總有吃飽的時候,這就意味著忽略了消化飽和因素,與實際情況不太相符.因此研究具有飽和因素的功能反應函數更加符合實際情況,而具有Holling-Ⅱ功能的反應函數
就有飽和關系.本文研究了捕食者Y(t)滿足Logistic方程,且其數量按照Logistic方式增長的模型
(2)
其中:X為食餌種群密度;Y為捕食者種群密度;r為食餌內稟增長率;e∈(0,1)為氣象環境對食餌種群密度的影響因子;K為環境容納量,可解釋為食餌所取作物狀況;a為捕食者的捕食率;β∈[0,1)為食餌逃避率,即捕食種群能捕捉到食餌數量為(1-β)X(t);c∈(0,1]為捕食者捕食食餌的轉化率;d為捕食者的死亡率.根據生態學意義可知模型(2)的初始條件為X(0)=X0>0,Y(0)=Y0>0.
2 平衡點的存在性和穩定性
當n≤t≤n+1(n=0,1,2,…)時,系統(2)轉化為
(3)
對(3)式兩端從n到t積分,并令t→n+1,得
(4)
通過簡單計算可得:對于任何參數,系統存在不動點E0(0,0),E1(K,0);當ac-d>0,K>K0時,系統(4)存在唯一正平衡點[3]
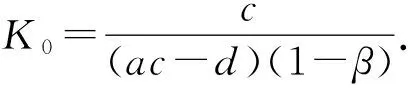
定理2.1系統(4)的平凡平衡點E0(0,0)是鞍點.
證明系統(4)的Jacobian矩陣為
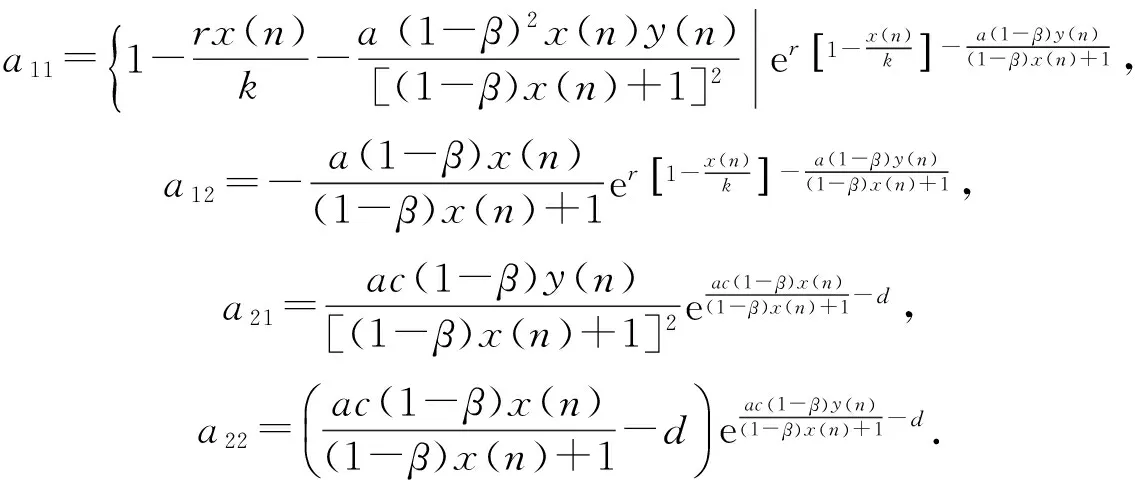
當(x(n),y(n))=(0,0)時,由文獻[5]可知系統(4)對應線性系統的特征方程為(λ-er)(λ-de-d)=0,從而λ1=er,λ2=-de-d.因為r>0,故|λ1|>1,|λ2|<1,所以平凡平衡點E0(0,0)是鞍點.
定理2.2(1) 當0
(2) 當r>2,k(1-β)(ac-d)>d時,平衡點E1(k,0)是不穩定的.
(3) 當r≠1,3,k(ac-d)(1-β)=d時,模型在平衡點E1(k,0)處產生Flip分支
證明模型(4)在平衡點E1(k,0)的Jacobian矩陣為
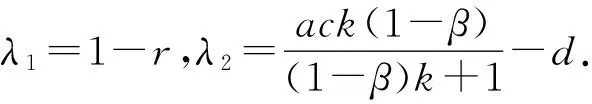
(1) 當0
(2) 當r>2,k(1-β)(ac-d-1)>1+d時,有|λ1|>1,|λ2|>1,所以E1(k,0)是不穩定的.
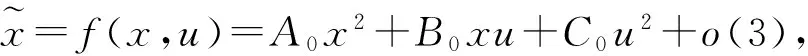
成立,則系統(3)在無病平衡點E1(k,0)處產生Flip分支.
(1) 若d(1+ac-d)K-(ac+(1+ac-d)d)K0<0,且
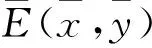
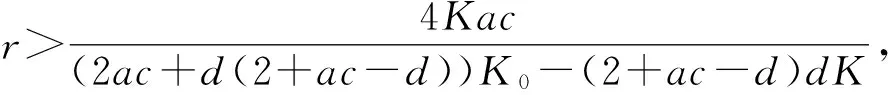
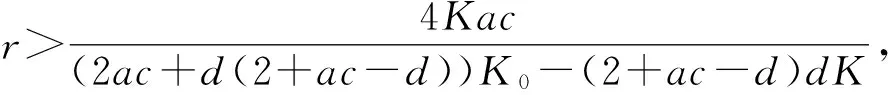
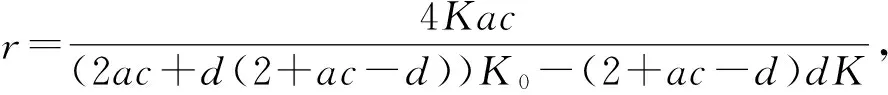
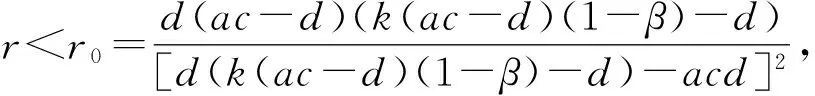
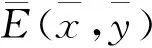
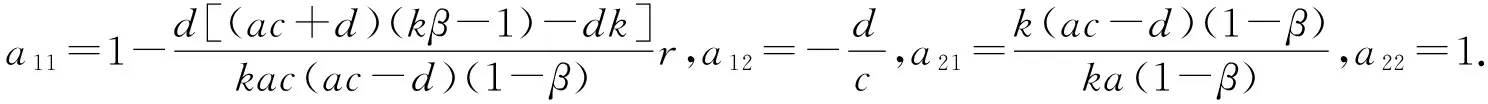
由于正平衡點的穩定性由特征方程的特征根決定,令p(λ)=λ2+μ1λ+μ2,可得

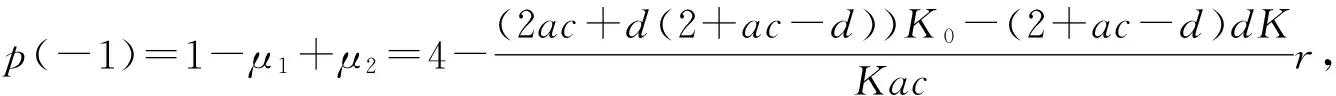
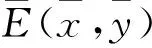
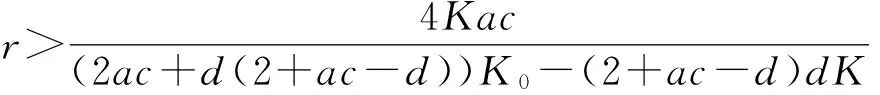
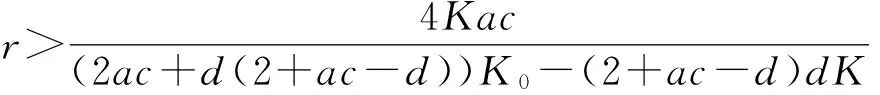
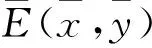
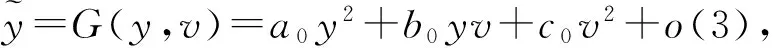
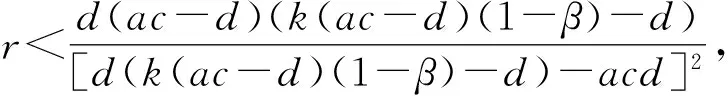
3 分支解的存在性和穩定性
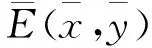
以及特征根
設p,q分別是對應于特征值eiθ0,e-iθ0的特征向量,則
Aq=eiθ0q,ATp=e-iθ0p.
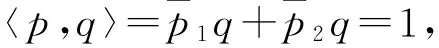
通過計算系統可表示為
其中:O(‖x‖4)是高階無窮小量;B(x,y)和C(x,y,z)是多重線性函數,且在坐標下的分量為
于是:
具有N-S分支的系統出現的閉不變曲線方向,可以用下面公式計算:
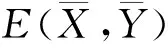
4 數值模擬
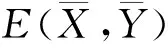
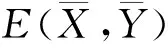
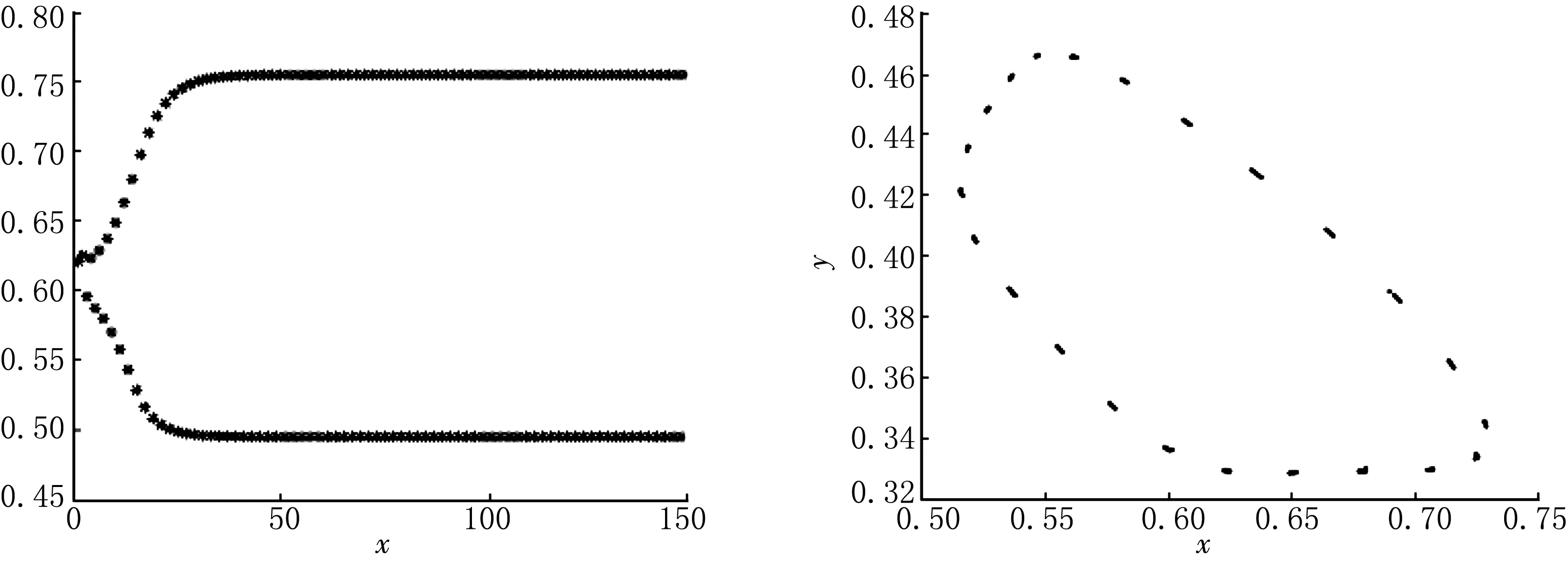
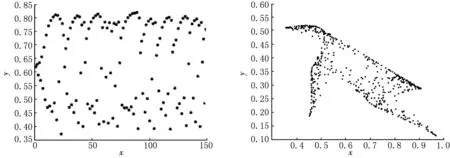
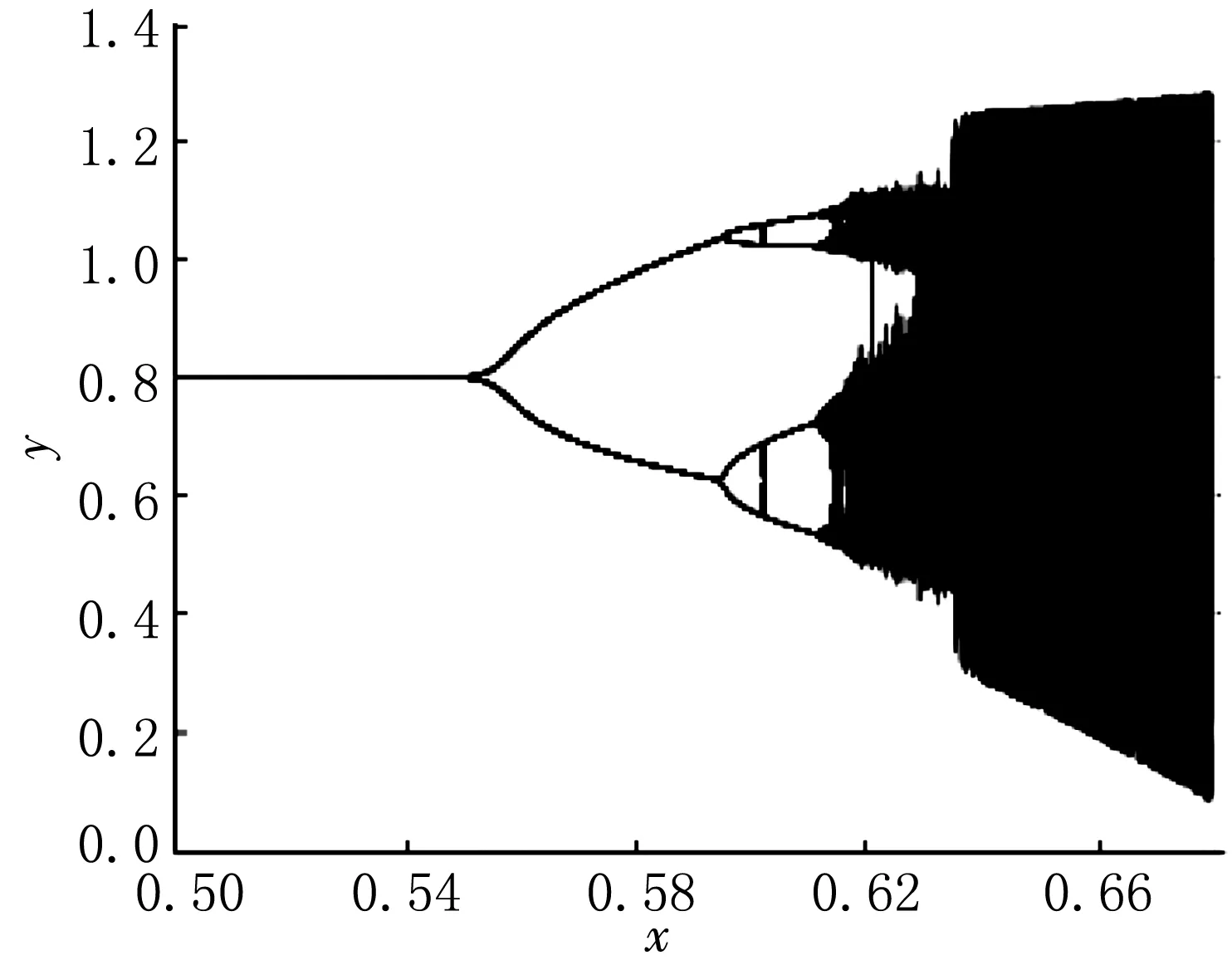
情形Ⅲ取參數值d=0.01,c=0.1,β=0.1,a=0.4,K=10.根據定理計算可知當r>r0>0.712時,差分方程(4)對初值迭代解非常敏感,看不出穩定的平衡點,系統已經失穩,產生混沌現象,見圖3—4.
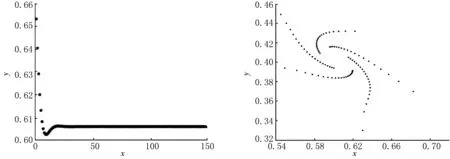
圖1 r 圖2 0.67 圖3 r>r0>0.712時N-S分支解的平面和相平面圖 圖4 混沌分岔圖 [參考文獻] [1]馬知恩.傳染病動力學的數學建模與研究[M].北京:科學出版社,2004:1-26. [2]LIU XIAO LI,XIAO DONG MEI.Complex dynamic behaviors of a discrete-time predator-prey system[J].Chaos Solitons and Fractals,2007,32(2):80-94. [3]LIU P,GOPALSAMY K.Global stability and chaos in a population model with piecewise constant arguments[J].Applied Mathematics and Computation,1999,101(1):63-88. [4]陳斯養,張艷.具有分段常數變量的捕食-被捕食模型的分支分析[J].蘭州大學學報(自然科學版),2012,48(3):103-112. [5]王烈,陳斯養.帶有分段常數變量的Lorenz系統的穩定性和分支[J].應用數學,2014,27(4):805-811. [6]張錦炎.常微分方程幾何理論與分支問題[M].北京:北京大學出版社,1987:69-95. [7]KUZNETSOV YURI A.Elements of applied bifurcation theory[M].New York:Springer-Verlag,2004:106-139.