2-距離空間中(ψ,φ,θ)-壓縮映象的公共不動點定理
劉麗亞,谷 峰
(杭州師范大學理學院,浙江 杭州 310036)
1 預備知識
1963年,G?lhler[1]首次引入了2-距離空間的概念,并較為深入地討論了這一空間的拓撲性質.1976年,Iséki等[2]開始研究關于2-距離空間中映象的不動點問題.隨后,2-距離空間中的不動點理論得到了較大發展.[3-9]受上述文獻啟發,本文在完備的2-距離空間中,引入一類新的(ψ,φ,θ)-型壓縮條件,并在此條件下研究重合點和公共不動點的存在性和唯一性問題,得到了一個新的公共不動點定理,在很大程度上推廣了相關文獻的一些結果.
定義1[9]設X是非空集,d:X×X×X→[0,+∞),滿足:
(1) 對每一對點a,b∈X,a≠b,存在一點c∈X,使得d(a,b,c)≠0;
(2)d(a,b,c)=0,當且僅當a,b,c中至少有二元相等;
(3)d(a,b,c)=d(a,c,b)=d(b,c,a)=d(b,a,c)=d(c,a,b)=d(c,b,a);
(4)d(a,b,c)≤d(a,b,x)+d(a,x,c)+d(x,b,c),其中x∈X.
則稱(X,d)為2-距離空間.
定義2[9](1) 序列{xn}稱為2-距離空間(X,d)中的收斂序列,如果存在x∈X,使得

(2) 設{xn}是2-距離空間(X,d)中的序列.{xn}稱為X中的Cauchy列,如果
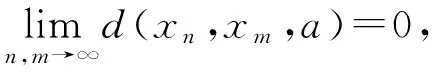
(3) 2-距離空間(X,d)稱為完備的,如果X中的每一Cauchy列都是X中的收斂列.
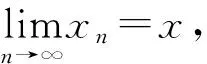

定義3[9]設{xn}是2-距離空間.d稱為是X上的連續2-距離,如果它關于三個變量中的兩個序列連續.
定義4[10]設(X,?)為2-距離空間(X,d)的一個偏序集,F:X→X,ɡ:X→X為兩個映象.則:
(1) 稱F是ɡ-不減的,如果?x1,x2∈X,ɡx1?ɡx2?Fx1?Fx2;
(2) 稱F是ɡ-不增的,如果?x1,x2∈X,ɡx1?ɡx2?Fx1Fx2.
定義5[11]稱x∈X是映象對F:X→X和ɡ:X→X的重合點,如果Fx=ɡx.
定義6[11]稱x∈X是映象對F:X→X和ɡ:X→X的公共不動點,如果Fx=ɡx=x.
定義7[11]設X為非空集,x∈X.映象對F:X→X和ɡ:X→X稱為在x處是可交換的,若ɡFx=Fɡx.
引理1[1]設(X,d)是完備的2-距離空間,{yn}是X中的序列,滿足
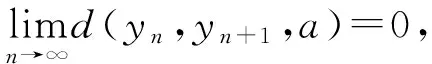
若{yn}不是X中的Cauchy列,則必存在某a0∈X,ε0>0以及正整數列{mi},{ni},使得:
(ⅰ)mi>ni+1,ni→∞(i→∞);
(ⅱ)d(ymi,yni,a0)≥ε0,d(ymi-1,yni,a0)<ε0,i=1,2,3,….
2 主要結果
本文假設ψ,φ和θ為以下三種類型的函數[12]:
(Ⅰ) 函數ψ:[0,∞)→[0,∞)滿足:(1)ψ是非減的且關于每個變元是連續的;(2)ψ(t)=0,當且僅當t=0.
(Ⅱ) 函數φ:[0,∞)→[0,∞)滿足:(1)φ是下半連續的;(2)φ(t)=0,當且僅當t=0.
(Ⅲ) 函數θ:[0,∞)→[0,∞)滿足:(1)θ是連續的;(2)θ(t)=0,當且僅當t=0.
定理1設(X,?)是2-距離空間(X,d)上的偏序集.ɡ:X→X為X上的自映象,映象F:X→X是ɡ-不減的,且與ɡ在重合點處可交換.?x0∈X使得ɡx0?Fx0.對于?x,y,a∈X,滿足
ψ(d(Fx,Fy,a))?ψ(M(x,y))-φ(M(x,y))+Lθ(N(x,y)).
(1)
其中:實數L≥0;
N(x,y)=min{d(ɡx,Fx,a),d(ɡy,Fy,a),d(ɡx,Fy,a),d(ɡy,Fx,a)}.
如果F(x)?ɡ(X),且ɡ(X)是完備的,則ɡ和T在X中有公共不動點.
證明由已知條件,?x0∈X滿足ɡx0?Fx0.又由于F(x)?ɡ(X),所以?x1∈X,使得ɡx1=Fx0.同理可知,?x2∈X使得ɡx2=Fx1.又由ɡx0?Fx0可知ɡx0?ɡx1.由于映象F是ɡ-不減的,所以
ɡx1=Fx0?Fx1=ɡx2.
依次類推,可得到X中的一個序列{xn},ɡxn+1=Fxn,n=0,1,2,…,滿足
ɡx0?ɡx1?ɡx2?…?ɡxn?ɡxn+1?….
(2)
在(1)式中令(x,y)=(xn,xn+1),由(2)式可得
ψ(d(ɡxn+1ɡxn+2,a))=ψ(d(Fxn,Fxn+1,a))≤
ψ(M(xn,xn+1))-φ(M(xn,xn+1))+Lθ(N(xn,xn+1)).
(3)
其中
(4)
N(xn,xn+1=min{d(ɡxn,Fxn,a),d(ɡxn+1,Fxn+1,a),d(ɡxn,Fxn+1,a),d(ɡxn+1,Fxn,a)}=
min{d(ɡxn,ɡxn+1,a),d(ɡxn+1,ɡxn+2,a),d(ɡxn,ɡxn+2,a),d(ɡxn+1,ɡxn+1,a)}=0.
(5)
在(3)式中令a=ɡxn,那么(4)式可整理為
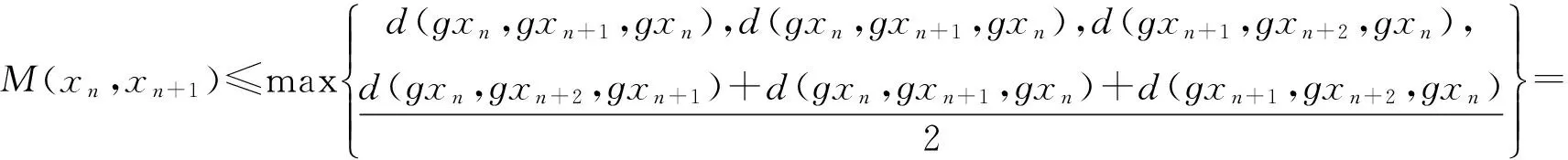
(6)
當a=ɡxn時,結合(5)和(6)式,(3)式可整理為
ψ(d(ɡxn+1ɡxn+2,ɡxn))=ψ(d(Fxn,Fxn+1,ɡxn))≤
ψ(d(ɡxn,ɡxn+2,ɡxn+1))-φ(d(ɡxn,ɡxn+2,ɡxn+1)).
當d(ɡxn,ɡxn+2,ɡxn+1)>0時,上式出現矛盾,即
d(ɡxn,ɡxn+2,ɡxn+1)=0,?n=0,1,2,….
(7)
當d(ɡxn,ɡxn+1,a)
M(xn,xn+1)=d(ɡxn+1,ɡxn+2,a).
再由(3)和(5)式,
ψ(d(ɡxn+1ɡxn+2,a))≤ψ(d(ɡxn+1,ɡxn+2,a))-φ(d(ɡxn+1,ɡxn+2,a)).
此時結果出現矛盾,故假設不成立,即
d(ɡxn,ɡxn+1,a)≥d(ɡxn+1,ɡxn+2,a),n=0,1,2,….
(8)
由(8)式可以看出,序列{d(ɡxn,ɡxn+1,a)}是單調遞減的非負實數列,因此?δ≥0,使得

(9)
根據(3),(7)和(8)式,
ψ(d(ɡxn+1ɡxn+2,a))≤ψ(d(ɡxn,ɡxn+1,a))-φ(d(ɡxn,ɡxn+1,a)).
(10)
如果δ>0,在(10)式兩邊令n→∞,同時由ψ和φ的性質可得
ψ(δ)≤ψ(δ)-φ(δ)<ψ(δ).
矛盾.于是證得δ=0,即

(11)
接下來證明

(12)
若不然,由引理1知必存在某個a0∈X,某個ε0>0以及正整數列{mi},{ni},使得:
(ⅰ)mi>ni+1,ni→∞(i→∞);
(ⅱ)d(ɡxni,ɡxmi,a0)≥ε0,d(ɡxni,ɡxmi-1,a0)<ε0,i=1,2,3,….
由三角形面積不等式和假設(Ⅱ)得
d(ɡxni,ɡxmi,a0)≤d(ɡxni,ɡxmi,ɡxni+1)+d(ɡxni,ɡxni+1,a0)+d(ɡxni+1,ɡxmi,a0).
在上式兩邊令i→∞,并由(11)式和假設(Ⅱ)得

即
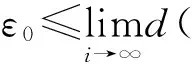
(13)
再由不等式關系得
d(ɡxmi-1,ɡxni+1,a0)≤d(ɡxmi-1,ɡxni+1,ɡxni)+
d(ɡxmi-1,ɡxni,a0)+d(ɡxni,ɡxni+1,a0),
d(ɡxni,ɡxmi,a0)≤d(ɡxni,ɡxmi,ɡxmi-1)+
d(ɡxni,ɡxmi-1,a0)+d(ɡxmi-1,ɡxmi,a0).
在上面兩個式子中分別令i→∞,并由(11)式和假設(Ⅱ)得
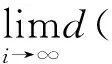
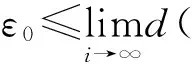
進一步整理得
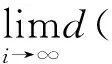
(14)
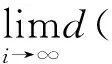
(15)
由(1)式,
ψ(d(ɡxni+1,ɡxmi,a0))=ψ(d(Fxni,Fxmi-1,a0))≤
ψ(M(xni,xmi-1))-φ(M(xni,xmi-1))+Lθ(N(xni,xmi-1)).
其中
N(xni,xmi-1)=
min{d(ɡxni,Fxni,a0),d(ɡxmi-1,Fxmi-1,a0),d(ɡxni,Fxmi-1,a0),d(ɡxmi-1,Fxni,a0)}=
min{d(ɡxni,ɡxni+1,a0),d(ɡxmi-1,ɡxmi-1,a0),d(ɡxni,ɡxmi,a0),d(ɡxmi-1,ɡxni+1,a0)}.
將上式兩邊令i→∞,并由(11),(13)—(15)式和假設(Ⅱ)得

即
ψ(ε0)≤ψ(ε0)-φ(ε0)<ψ(ε0).
矛盾,從而(12)式成立.
又因為ɡ(X)是完備的,于是?x∈X,滿足

(16)
再由(1)式,
ψ(d(Fx,ɡxn+1,a))=ψ(d(Fx,Fxn,a))≤ψ(M(x,xn))-φ(M(x,xn))+Lθ(N(x,xn)).
其中

N(x,xn)=min{d(ɡx,Fx,a),d(ɡxn,Fxn,a),d(ɡx,Fxn,a),d(ɡxn,Fx,a)}=
min{d(ɡx,Fx,a),d(ɡxn,ɡxn+1,a),d(ɡx,ɡxn+1,a),d(ɡxn,Fx,a)}.
將上式兩邊令n→∞,并由(11)式和注1得

由ψ和φ的性質可得d(Fx,ɡx,a)=0,進而ɡx=Fx.由此可知x是ɡ和F的重合點.
現證ɡ和F的重合點唯一.
事實上,假設?x*∈X,x*≠x,使得ɡx*=Fx*.由(1)式可得
ψ(d(ɡx,ɡx*,a))=ψ(d(Fx,Fx*,a))≤ψ(M(x,x*))-φ(M(x,x*))+Lθ(N(x,x*)).
(17)
其中
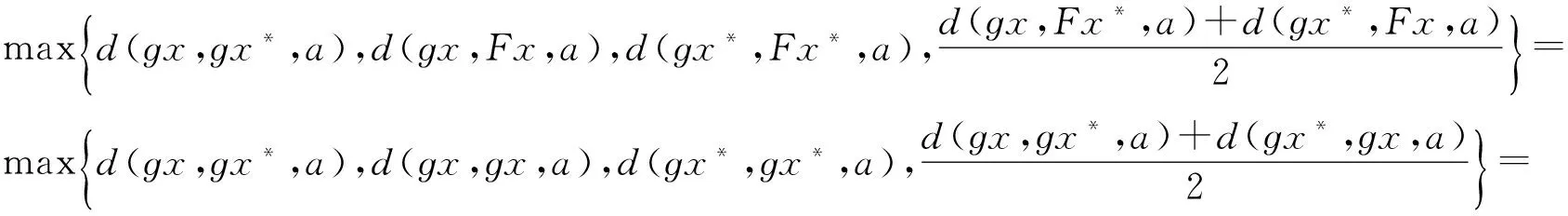
(18)
N(x,x*)=min{d(ɡx,Fx,a),d(ɡx*,Fx*,a),d(ɡx,Fx*,a),d(ɡx*,Fx,a)}=
min{d(ɡx,ɡx,a),d(ɡx*,ɡx*,a),d(ɡx,ɡx*,a),d(ɡx*,ɡx,a)}=0.
(19)
將(18)和(19)式代入(17)式可得
ψ(d(ɡx,ɡx*,a))≤ψ(d(ɡx,ɡx*,a))-φ(d(ɡx,ɡx*,a)).
由ψ和φ的性質可知d(ɡx,ɡx*,a)=0,從而ɡx=ɡx*.即證得ɡ和F的重合點唯一.
令μ=ɡx=Fx,則Fμ=F(ɡx)=ɡ(Fx)=ɡμ.從而μ也為ɡ和F的重合點,由ɡ和F的重合點的唯一性,可得ɡμ=Fμ=ɡx=Fx=μ,即ɡμ=Fμ=μ.從而可得μ是ɡ和F的公共不動點,證畢.
推論1設(X,?)是完備2-距離空間(X,d)上的偏序集且X是完備的.映象F:X→X,實數L≥0,且?x,y,a∈X,滿足
ψ(d(Fx,Fy,a))≤ψ(M(x,y))-φ(M(x,y))+Lθ(N(x,y)),
其中
N(x,y)=min{d(x,Fx,a),d(y,Fy,a),d(x,Fy,a),d(y,Fx,a)}.
則F在X中有不動點.
證明令定理1中的自映象ɡ為恒等映象I,即可證得結論.
推論2設(X,?)是2-距離空間(X,d)上的偏序集.ɡ:X→X為X上的自映象,映象F:X→X是ɡ-不減的,且與ɡ在重合點處可交換.?x0∈X使得ɡx0?Fx0,對于?x,y,a∈X,滿足
如果F(x)?ɡ(X),且ɡ(X)是完備的,則ɡ和F在X中有公共不動點.
3 在積分方程中的應用
令X=C[I]為所有I=[0,1]上的連續函數全體,受文獻[1]的啟發,考慮積分方程在X中是否存在解

(20)
這里函數T:I×X→R.首先,定義偏序關系:
x?y?x(t)≤y(t),?t∈I.
假設:
(ⅰ)h:I→R,k:I×I→R,t∈I為連續函數;

(ⅲ) 對于?x,y,a∈X,如果x?y,那么有

令d:X×X×X→[0,+∞),

容易看出(X,?,d)是偏序2-距離空間.

x0?x1?x2?…?xn?xn+1?…,
且{xn}收斂于一點u∈X,即xn?u,?n∈N,則方程(20)在X中有解.
證明定義函數F,ɡ:X→X分別為

ɡx=x(t),?x∈X,t∈I.
由條件(ⅱ)得
ɡx(t)?ɡy(t)?Fx(t)?Fy(t),?x,y∈X,t∈I.
由條件(ⅳ),ɡx0?Fx0.又由條件(ⅲ)可知?x,y,a∈X,且x?y,Fx?Fy.
進一步有
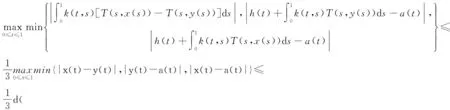
其中
N(x,y)=min{d(ɡx,Fx,a),d(ɡy,Fy,a),d(ɡx,Fy,a),d(ɡy,Fx,a)}.
綜上,定理1中的所有條件都滿足,于是?x∈X,使得Fx(t)=x(t),即方程(20)在X中有唯一解.
[參考文獻]
[2]ISЁKI K.Fixed point theorems in 2-meric spaces[J].Math Seminar Notes Kobe Univ,1975,3(1):133-136.
[3]DUNG N V,LE HANG V T.Fixed point theorems for weak C-contractions in partially ordered 2-metric spaces[J].Fixed Point Theory and Applications,2013,161(1):1-12.
[4]LAHIRI B K,DAS P,DEY L K.Cantor’s theorem in 2-metric spaces and its applications to fixed point problems[J].Taiwan J Math,2011,15(1):337-352.
[5]ALIOUCHE A,SIMPSON C.Fixed points and lines in 2-metric spaces[J].Adv Math,2012,229(1):668-690.
[6]CONSTANTIN A.Common fixed points of weakly commuting mappings in 2-metric spaces[J].Math Japon,1991,36(3):507-514.
[7]LIU Z Q,ZHANG F R.Characterizations of common fixed points in 2-metric space[J].Rostock Math Kolloq,2001,55(1):49-64.
[8]DUBEY R P.Some fixed point theorems on expansion mappings in 2-metric spaces[J].Pure Appl Math Sci,1990,32(1):33-37.
[9]張石生.不動點理論及其應用[M].重慶:重慶出版社,1984:350-412.
[10]BHASKAR T G,LAKSHMIKANTHAM V.Fixed point theorems in partially ordered metric spaces and applications[J].Nonlinear Anal,2006,65(7):1379-1393.

[12]谷峰,高偉,田巍.不動點定理與非線性算子迭代序列的收斂性[M].哈爾濱:黑龍江科學技術出版社,2002:75-93.

