空基多雷達航跡抗差關聯算法

齊林,劉瑜，任華龍，何友

1. 海軍航空大學 信息融合研究所，煙臺 264001 2. 海軍青島雷達聲吶修理廠，青島 266000

航跡關聯是分布式多雷達數據融合[1-2]的一項關鍵技術，用于判別不同雷達上報的同源航跡，得到觀測環境清晰完整的態勢信息。航跡關聯是系統誤差配準[3-4]和態勢融合的前提，同時系統誤差的影響使估計航跡與真實航跡存在較大偏差，需要誤差配準技術對量測數據進行校正。因此，系統誤差存在時的航跡關聯和誤差配準互為前提，給問題的解決帶來更大困難。

實際情況下，系統誤差普遍存在于雷達量測數據中。特別是處于高速高機動運動狀態的空基雷達，系統誤差受到多種因素的影響，統計特性未知。傳統航跡關聯算法[5-7]僅考慮隨機誤差的影響，假設目標運動狀態估計服從以真實運動狀態為期望的高斯分布，此類算法在系統誤差存在時效果惡化嚴重。

文獻[8-12]提出基于參照拓撲特征的航跡關聯算法(RET算法)用于處理雷達航跡抗差關聯問題。算法認為在全局直角坐標系中，目標間相對位置關系不受系統誤差的影響，以此作為航跡關聯的依據。此類算法存在一定的缺陷。第一，系統誤差是距離和角度上的量測偏差，經坐標變換到以融合中心為原點的全局直角坐標系中，系統誤差不再體現為位置上的固定偏差。第二，拓撲關聯基于多維分配準則處理多義性問題，但無法給出理論上的航跡關聯門限，造成錯誤關聯率較高。

由于航跡關聯和誤差配準互為前提，分別處理難度較大，文獻[13-14]提出同時實施關聯和配準的方法。單純基于目標運動特征的航跡關聯技術存在性能不穩定等問題，Mori等將目標屬性等特征信息加入狀態矢量，提出特征輔助航跡關聯方法[15-16]。上述兩類方法因計算復雜和屬性信息缺失實用性受限。

文獻[17]提出一種計算流程簡便、適用于工程實踐的基于距離檢測的自動識別系統(Automatic Identification System, AIS)和對海雷達航跡抗差關聯算法，在目標稀疏環境下性能良好，在目標密集環境下性能較差。

文獻[18-19]基于等價量測一階泰勒展開推導全局直角坐標系中狀態估計矢量分解方程。文獻[20]在此基礎上定義航跡距離矢量，基于系統誤差矢量對消得到兩雷達航跡抗差關聯條件，該算法具有較高的關聯準確性和復雜環境適應能力。

大多現有的航跡抗差關聯算法僅適用于兩雷達環境，但兩個以上雷達航跡間的融合處理在實際應用中普遍存在。多雷達數據融合情況下，為減少雷達兩兩關聯產生的冗余計算，需要研究適用于兩個以上雷達的航跡抗差關聯算法。本文在航跡距離矢量的基礎上推導適用于3個及3個以上雷達的航跡關聯條件和多雷達航跡關聯流程，提出空基多雷達航跡抗差關聯算法。

1 問題描述

空基多平臺信息融合系統中，每個運動平臺搭載雷達探測跟蹤環境中的多個運動目標，形成各自的環境態勢信息，并基于航跡關聯技術解決重疊覆蓋空間中的去重復跟蹤問題。假設環境中有若干個雷達和目標，其中目標T分別為雷達a、b、c探測到的第i、j、k個目標，某時刻雷達與目標的位置分布情況如圖 1所示。

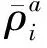
(1)

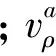
(2)

雷達b、c對T的量測矢量同理可知。

運動平臺不能作為目標跟蹤坐標系的原點，通常選擇平臺外一固定點作為目標跟蹤慣性坐標系的原點。圖 2中Oa(xoa,yoa)表示雷達a選取的固定參考點，將雷達量測轉換到以Oa(xoa,yoa)為原點的慣性坐標系中，基于轉換量測Kalman濾波[21]得到目標狀態估計。空基多平臺偵察監視環境存在探測距離遠、目標分布密集、系統誤差時變、雷達上報目標不一致等復雜情況，傳統航跡關聯算法失效；現有的航跡抗差關聯算法大多僅適用于兩雷達環境，需研究適用于兩個以上雷達的航跡抗差關聯算法。

2 算法描述

2.1 航跡距離矢量

在以融合中心O(0,0)為原點的全局直角坐標系中，狀態估計矢量分解方程如式(3)所示，推導流程見文獻[18-19]。

(3)

(4)

式(3)建立了全局直角坐標系下目標狀態估計與目標真實狀態、系統誤差和隨機誤差之間的加性關系。文獻[20]定義了航跡距離矢量:

(5)

(6)

式中：

(7)

(8)

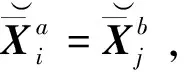
(9)

2.2 3個雷達航跡關聯條件

雷達a、b、c分別上報航跡i、j、k，航跡i分別與航跡j、k對消得到距離矢量，如果航跡i、j、k源自同一目標，則滿足：

(10)

(11)

將4維等式(10)、等式(11)拆分成兩個2維等式：

(12)

(13)

(14)

(15)

令

(16)

(17)

則

(18)

(19)

令

(20)

(21)

(22)

(23)

(24)

式中：nx為狀態矢量的維數，這里nx=4。如果雷達a、b、c上報的航跡i、j、k源自同一目標，式(24)成立，否則不成立，因此可基于式(24)判斷3個雷達上報航跡是否關聯。

2.3 3個以上雷達航跡關聯條件

討論3個以上雷達航跡抗差關聯條件，以四雷達情況為例。假設雷達a、b、c、d上報的航跡i、j、k、l，航跡i分別與航跡j、k、l對消得到距離矢量，如果航跡i、j、k、l源自同一目標，式(10)、式(11)和式(25)成立：

(25)

參照2.2節的推導，可知

(26)

(27)

(28)

(29)

式中：

(30)

(31)

(32)

理想情況下，式(24)、式(26)、式(28)中任意2式成立則第3式成立。將式(24)、式(26)、式(28)中任意2式成立作為航跡i、j、k、l關聯的條件，如果3式中僅1式成立，判斷該式包含的3條航跡關聯，與第4條航跡不關聯。

基于相同思路，容易將上述推導推廣到4個以上雷達的情況。當雷達個數為m(m>2)時，判斷每組雷達航跡是否關聯需滿足(m-1)(m-2)/2個條件。

2.4 多雷達航跡抗差關聯流程

當雷達個數為m時，基于2.2節和2.3節的多雷達航跡關聯條件分別判斷不同雷達上報的m條航跡是否源自同一目標。然而雷達上報目標不一致的情況下，不同雷達上報的m條航跡的組合可能都不滿足關聯條件。此時需要降低組合中的航跡數，判斷航跡個數為m-1的組合是否關聯，直到為每個雷達至少找出一條航跡與其他雷達的航跡關聯或組合中的航跡數降至2。實際上，航跡關聯的目的是消除系統誤差，得到清晰一致的環境態勢。通過航跡關聯處理能為每個與其他雷達有同源航跡的雷達準確的找到至少一條與其他雷達同源的航跡即可。

(33)

作為航跡i、j、k、l的關聯代價，選取使全局代價最小的分配矩陣確定航跡的關聯關系。

當雷達和目標數分別為m和n時，文獻[20]所述兩雷達航跡抗差關聯算法，雷達兩兩關聯的計算復雜度為

(34)

本文算法的計算復雜度為

Tpro(m,n)=(m-1)n2Td+

(35)

式中：Td為求一次4維距離矢量的計算復雜度;T4χ2為求一次4維χ2檢驗的計算復雜度，T2χ2為求一次2維χ2檢驗的計算復雜度。

當m>2、n>2時，Tt2t(m,n)>Tpro(m,n)，本文所述的多雷達航跡航跡抗差關聯算法相比于雷達兩兩關聯具有更低的計算復雜度，能顯著降低雷達兩兩關聯需要的冗余計算。

綜上所述，空基多雷達航跡抗差關聯流程如圖3所示，其中對m條航跡的關聯檢驗針對的是不同雷達上報的m條航跡，具體流程如圖4所示。

3 仿真驗證及結果分析

3.1 仿真環境設置及評價指標

為驗證本文算法的性能，設置如下的仿真環境：某空域有飛行目標n=16批次，關聯時刻目標位置在空域(x1,x2)×(y1,y2)中均勻分布，x1=100 km，x2=150 km，y1=100 km，y2=150 km。目標勻速等高飛行，水平面內初始速度v0和初始航向d0分別服從均勻分布，v0～U(100, 200) m/s，d0～U(0, 2)π rad，雷達采樣周期T=4 s，航行周期數Time=100。

空基平臺1的初始位置為(0, 5) km，初始速度為(150, 0) m/s，平臺2的初始位置為(125, 0) km，初始速度為(0, 100) m/s，平臺3的初始位置為(250, 0) km，初始速度為(0, 200) m/s。平臺按初始速度做勻速直線運動，并向位置為(0, 0) m的融合中心實時上報估計航跡。運動平臺不能作為目標跟蹤的坐標系原點，雷達分別選取初始位置作為目標跟蹤慣性坐標系的原點坐標。雷達量測隨機誤差分別服從均值為零，距離誤差標準差σρ=100 m、方位角誤差標準差σθ=0.3°的高斯分布。雷達系統誤差時變，大小服從0到誤差上限間的均勻分布，雷達1的誤差上限Δρ1=-1 000 m、Δθ1=-1°，雷達2的誤差上限Δρ2=0 m、Δθ2=0°，雷達3的誤差上限Δρ3=1 000 m、Δθ3=1°。3個雷達分別上報14批次目標航跡，其中有10批次同源航跡。真實航跡與雷達估計航跡如圖 5(a)所示，單個時刻目標真實點跡與雷達估計點跡如圖 5(b)所示。

為描述算法的關聯效果，這里定義航跡關聯的評價指標。正確關聯率為

(36)

錯誤關聯率為

(37)

式中：n為一次實驗中真實目標個數；n′為雷達上報的同源航跡個數，n′≤n；nca為正確關聯的目標個數；nfa為錯誤關聯的目標個數；Rca為正確關聯率，即一次實驗中正確關聯的目標個數與同源航跡個數的比值；Rfa為錯誤關聯率，即一次實驗中錯誤關聯的目標個數與真實目標個數的比值。實驗結果由50次蒙特卡羅仿真求均值得到，Rca和Rfa分別為關聯結果中的平均正確關聯率和平均錯誤關聯率。

為驗證本文算法性能的優越性，在仿真環境中利用本文算法、基于目標參照拓撲特征的航跡關聯算法(RET算法)和基于距離檢測的可信關聯算法(Confidential算法)實施航跡關聯。RET算法以目標間相對位置關系作為關聯依據，對系統誤差和隨機誤差造成的目標位置偏差具有較強的適應性。Confidential算法是一種計算簡便的工程化算法，在目標稀疏環境中性能良好。

3.2 目標密集環境適應性實驗

為驗證算法對環境中目標密集程度的適應能力，保持目標個數不變，改變目標分布空域的大小，比較3種算法的關聯效果，如圖6所示。

隨著空域長度逐漸增大，目標密度逐漸減小，本文算法的Rca在70%上下浮動，Rfa接近于0。RET算法的Rca隨目標密度減小由40%上升至95%再下降至50%，極值出現在空域長度為20 km時，Rfa由50%下降至接近于0。Confidential算法在空域長度小于40 km時性能較差，隨著目標密度減小，性能逐漸提高。

本文算法基于狀態估計矢量的分解對消構建χ2檢驗量，算法性能幾乎不受目標密集程度的影響，具有較好的穩健性。RET算法基于目標參照拓撲特征實施航跡關聯，在目標密集環境易將非同源航跡誤判成同源航跡，造成Rca較低，Rfa較高。距離系統誤差造成全局直角坐標系中目標間距伸縮，方位角相差越大的目標間距伸縮量越大。在目標稀疏環境中，互為參照的目標方位角相差較大，不同雷達上報的同源航跡參照拓撲特征不一致，RET算法Rca較低。Confidential算法要求一簇同源航跡周圍沒有異源航跡，適用于目標稀疏環境，在目標密集環境中性能較差。

3.3 隨機誤差適應性實驗

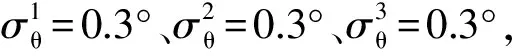
如圖7(a)所示，距離誤差標準差σρ由20 m增大至200 m，本文算法Rca由0逐漸增大至80%，Rfa接近于0。σρ由20 m增大至60 m，RET算法和Confidential 算法的Rca由35%增大至75%，σρ繼續增大，Rca在75%上下浮動，RET算法的Rfa始終在5%上下浮動，Confidential 算法的Rfa始終在15%上下浮動。如圖 7(b)所示，方位角誤差標準差σθ由0.1°增大至1.0°，本文算法的Rca由0升高至75%再下降至10%，Rfa接近于0。RET算法和Confidential算法的Rca由80%左右逐漸下降至接近0，Rfa大于本文算法且隨σθ增大而增大。

在一定的范圍內，量測隨機誤差能抵消系統誤差造成的航跡偏差，因此系統誤差存在的條件下，3種算法的Rca隨σρ增大而升高。σθ造成的航跡偏差遠大于σρ，與雷達與目標間的距離成正比，σθ增大造成本文算法Rca先升高后降低，RET算法和Confidential算法的Rca降低明顯。

3.4 系統誤差適應性實驗

為驗證算法對系統誤差的適應能力，分別改變仿真參數中雷達的距離、方位角系統誤差上限，其他參數不變，比較本文算法和RET算法的關聯效果。雷達方位角誤差上限保持Δθ1=-1°、Δθ3=1°，距離誤差上限Δρ1在-200～-2 000 m等間隔分布，Δρ3在200～2 000 m等間隔分布，得到如圖 7(c)所示的關聯結果；雷達距離誤差上限保持Δρ1=-1 000 m、Δρ3=1 000 m，方位角誤差上限Δθ1在-0.2°～-2.0°等間隔分布，Δθ3在0.2°～2.0°等間隔分布，得到如圖 7(d)所示的關聯結果。

由圖 7(c)可知，距離誤差上限Δρ由200 m增大至2000 m，本文算法、RET算法、Confidential算法的Rca分別在65%、75%、70%上下浮動，本文算法的Rfa接近0，RET算法的Rfa在5%上下浮動、Confidential算法的Rfa在15%上下浮動。由圖 7(d)可知，方位角誤差上限Δθ由0.2°增大至2.0°，3種算法的Rca均有顯著下降，本文算法Rca最低。本文算法Rfa接近0；RET算法的Rfa在5%上下浮動；Confidential算法的Rfa由5%上升至27%。

距離系統誤差造成的航跡偏差較小，3種算法均對其有較強的適應性；方位角系統誤差造成的航跡偏差較大，隨著方位角系統誤差增大，3種算法性能都有顯著下降。本文算法基于狀態估計矢量分解對消推導多雷達航跡關聯條件，優點是能排除大部分非同源航跡，Rfa較低，缺點是門限比較嚴格導致方位角系統誤差較大時Rca較低。RET算法基于多維分配處理多義性問題，沒有嚴格的關聯門限，導致Rca和Rfa都比較高。

4 結 論

本文基于高斯隨機矢量統計特性推導出一種適用于復雜環境的空基多雷達航跡抗差關聯算法。

1) 本文算法能顯著減低多雷達情況下雷達兩兩關聯產生的冗余計算，計算復雜度較低。

2) 本文算法基于狀態估計矢量分解對消嚴格推導航跡關聯門限，在目標密集等復雜環境下仍能排除大部分非同源航跡，具有很低的錯誤關聯率，缺點是門限比較嚴格導致方位角系統誤差較大時正確關聯率較低。

3) 雷達量測系統誤差和隨機誤差都存在且系統誤差較大時，由于隨機誤差對系統誤差的抵消作用，航跡關聯正確率隨隨機誤差增大而提高。

參 考 文 獻

[1] BAR-SHALOM Y, FORTMANN T E. Tracking and data association[M]. Orlando: Academic Press INC., 1988: 266-272.

[2] 何友， 王國宏， 關欣. 信息融合理論及應用[M]. 北京: 電子工業出版社, 2010: 267-308.

HE Y, WANG G H, GUAN X. Information fusion theory with applications[M]. Beijing: Publishing House of Electronics Industry, 2010: 267-308 (in Chinese).

[3] LIN X D, BAR-SHALOM Y, KIRUBARAJAN T. Exact multi-sensor dynamic bias estimation with local tracks[J]. IEEE Transactions on Aerospace & Electronic Systems, 2004, 40(2): 576-590.

[4] ZHENG Z W, ZHU Y S. New least squares registration algorithm for data fusion[J]. IEEE Transactions on Aerospace & Electronic Systems, 2004, 40(4): 1410-1416.

[5] HE Y, ZHANG J W. New track correlation algorithms in a multi-sensor data fusion system[J]. IEEE Transactions on Aerospace & Electronic Systems, 2006, 42(4):1359-1371.

[6] 何友， 宋強， 熊偉. 基于傅里葉變換的航跡對準關聯算法[J]. 航空學報, 2010, 31(2): 356-362.

HE Y, SONG Q, XIONG W. A track registration-correlation algorithm based on Fourier transform[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2): 356-362 (in Chinese).

[7] 衣曉， 張懷巍， 曹昕瑩， 等. 基于區間灰數的分布式多目標航跡關聯算法[J]. 航空學報, 2013, 34(2): 352-360.

YI X, ZHANG H W, CAO X Y, et al. A track association algorithm for distributed multi-target systems based on gray interval numbers[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 352-360 (in Chinese).

[8] 石玥， 王鉞， 王樹剛， 等. 基于目標參照拓撲的模糊航跡關聯方法[J]. 國防科技大學學報, 2006, 28(4): 105-109.

SHI Y, WANG Y, WANG S G, et al. Fuzzy data association based on target topology of reference[J]. Journal of National University of Defence Technology, 2006, 28(4): 105-109 (in Chinese).

[9] TIAN W, WANG Y, SHAN X M, et al. Track-to-track association for biased data based on the reference topology feature[J]. IEEE Signal Processing Letters, 2014, 21(4): 449-453.

[10] 田威. 復雜環境下多傳感器航跡關聯與抗差處理[D]. 北京: 清華大學, 2014: 96-116.

TIAN W. Multi-sensor track-to-track association and bias removal in complex environments[D]. Beijing: Tsinghua University, 2014: 96-116 (in Chinese).

[11] ZHU H Y, HAN S Y. Track-to-track association based on structural similarity in the presence of sensor biases[J]. Journal of Applied Mathematics, 2014(1): 1-8.

[12] ZHU H Y, WANG W, WANG C. Robust track-to-track association in the presence of sensor biases and missed detections[J]. Information Fusion, 2016, 27: 33-40.

[13] LI Z, CHEN S, LEUNG H, et al. Joint data association, registration, and fusion using EM-KF[J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(2): 496-507.

[14] ZHU H, LEUNG H, YUEN K. A joint data association, registration, and fusion approach for distributed tracking[J]. Information Sciences, 2015, 324(C):186-196.

[15] MORI S, CHANG K C, CHONG C Y. Tracking performance evaluation-prediction of track purity[C]∥Proceeding of SPIE. Bellingham, WA: SPIE, 1989: 215-223.

[16] MORI S, CHANG K C, CHONG C Y. Performance prediction of feature-aided track-to-track association[J]. IEEE Transactions on Aerospace & Electronic Systems, 2014, 50(4): 2593-2603.

[17] 齊林， 崔亞奇， 熊偉， 等. 基于距離檢測的自動識別系統和對海雷達航跡抗差關聯算法[J]. 電子與信息學報, 2015, 37(8): 1855-1861.

QI L, CUI Y Q, XIONG W, et al. Anti-bias association algorithm for automatic identification system and radar based on bias detection[J]. Journal of Electronics & Information Technology, 2015, 37(8): 1855-1861 (in Chinese).

[18] ZHU H Y, CHEN S. Track fusion in the presence of sensor biases[J]. IET Signal Process, 2014, 8(9): 958-967.

[19] ZHU H Y, WANG C. Joint track-to-track association and sensor registration at the track level[J]. Digital Signal Processing, 2015, 41: 48-59.

[20] QI L, DONG K, LIU Y, et al. Anti-bias track-to-track association algorithm based on distance detection[J]. IET Radar, Sonar & Navigation, 2017, 11(2): 269-276.

[21] 何友， 修建娟， 關欣. 雷達數據處理及應用[M]. 3版. 北京: 電子工業出版社, 2013: 36-50.

HE Y, XIU J J, GUAN X. Radar data processing with applications[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2013: 36-50 (in Chinese).