聚焦核心展本質回歸樸實悟“通法”
——“雞兔同籠”教學新策略

何月豐　張永輝

【課前思考】

修訂后的人教版教材，“雞兔同籠”安排在四年級下冊。近兩年時間，筆者與學校四年級學科組對這節課進行了深入的思考與實踐，在以下幾個問題上，有了新的認識。

問題一：“雞兔同籠”該教哪種方法好？

“雞兔同籠”的解法眾多。修訂后的人教版教材將其安排在四年級下冊，這樣“砍去”了方程一法，但仍有畫圖、列表、假設，還有古代經典“抬腿法”。對于四年級的學生而言，畫圖是“幼稚”的——四年級的學生已經可以逐步擺脫具體的圖形，可以從抽象的數據進行理解了，因此，倘若把“畫圖”作為一種主要的方法來教，顯然幼稚了點；列表是“傻傻”的——實踐證明，在教師沒提醒、要求或提供表格的前提下，學生一般不會按著順序一個一個列表來尋求答案，尤其不會從“0”開始思考（雞兔同籠，怎么可能沒有雞或兔），因此，列表顯得傻傻的，是不符合學生學習心理的方法；抬腿法是“怪怪”的——首先，這個方法一部分學生很難理解，其次，這不是“通法”，當面對三輪車和自行車時，就很難實施了。如此看來，只剩下假設法了。所以筆者認為，四年級時“雞兔同籠”教學的主要方法應該是假設法。

問題二：假設法該如何教？

對“雞兔同籠”重點教假設法，是有質疑的，尤其是在四年級。因為許多學生面對假設法中的那一串算式，往往很難真正理解，更重要的是總會有一些學生到下課都不能理解，許多時候一節課下來，目標的達成度是偏低的。那么，如何教假設法就成了擺在我們面前的現實問題。對此，筆者認為需要關注兩點：一是假設法的本質是什么？二是學生面對假設法難理解的地方在哪里？厘清這兩個問題，也就厘清了假設法在課堂上的實施路徑。

當我們把一個數據較小的典型“雞兔同籠”問題給學生，如“6個頭、16只腳”，絕大部分學生通過獨立思考會得出答案。他們的方法中，較為普遍的一類是：先任意猜一個，如果沒對，調整一下再猜一個。因為數據較小，沒幾次就能猜對。很明顯，“猜”本身就是一種假設。我們所謂的“假設法”，無非是猜了一種極端情況（全部是雞或兔）。現在的問題是“沒猜對怎么辦？”假設法中極端的猜，顯然不能猜對，然后做的事情是調整。學生任意猜，沒猜對，接下來也是調整，直到正確為止。至此，可以看出假設法的本質：猜——調整。這也就成了假設法教學的重點。

問題三：假設法中學生難理解的地方在哪里？

多次實踐發現，學生第一次猜好后，接下來的調整有差異。低級水平：猜好后，不做分析，沒有方向的再任意猜一個；中級水平：猜好后，進行分析，明確接下來雞、兔的增減方向，再猜；高級水平：猜好后，進行分析，明確接下來雞、兔的增減方向，根據腳的數量關系，一次性調整到位。這里，高級水平其實就是我們所謂的“假設法”的做法。由此可見，第一次猜好后，“如何調整”是學生難理解的地方。

基于以上分析我認為，就四年級學生而言，解“雞兔同籠”方法的本質可以理解為“猜——調整”，重點是“沒猜對——怎么調整”，難點是“能不能一次調整到位”。這是一種樸實的方法，也是一種通用的方法。

基于以上思辨，筆者就“雞兔同籠”一課，制定了如下教學目標：

1.認識“雞兔同籠”，理解“猜——調整”解決問題的方法，并能進行簡單運用。

2.經歷嘗試、對比、分析等學習過程，發展數學推理能力。

3.感受數學的趣味性和數學學習的樂趣。

【過程設計】

一、認識“雞兔同籠”，理解“雞兔互換”規律

1.課件呈現問題：雞兔同籠,從上面數，有5個頭。 猜一猜，可能有幾只雞？幾只兔？

2.根據學生回答，依次板書出雞、兔數量，按順序排列（如圖所示）。

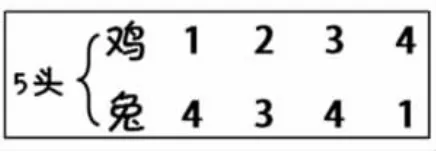
3.追問這些情況下腳一共有幾只，怎么算的。根據學生回答，依次板書出各種情況下腳的數量（如圖所示）。

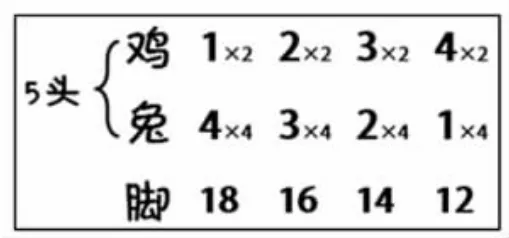
4.對比發現規律：增加1只雞，減少1只兔，腳的數量減少2（反之腳的數量增加2）。結合板書（畫圖：展現添上2只腳和去掉2只腳的過程），直觀理解這個道理，最終歸結為：把1只兔換成1只雞，腳減少2；把1只雞換成1只兔，腳增加2。

【設計意圖：通過這個環節的教學，讓學生感悟到1只雞與1只兔進行交換，腳的總數量會相差2，并直觀理解“相差2”是怎么發生的。由此，將畫圖法作為一種輔助理解的方法進行合理使用。】

二、初識“猜—調整”，嘗試運用方法

1.課件呈現問題：雞兔同籠,從上面數，有6個頭。猜一猜，可能有幾只雞？幾只兔？

2.學生猜一種情況，教師板書學生猜的情況（例如2只雞，4只兔），并計算出腳的數量（20）。

3.教師告之正確的腳數量（一般根據學生猜的那種情況的腳數量，增加2或者減少2即可，此處以腳數“22”為例），發現沒有猜對。追問：你能不能根據現在猜的情況，很快知道雞和兔正確應該是幾只嗎？

4.學生觀察思考，結合前面的學習經驗，通過一次調換，得到正確的結果。教師根據學生回答，結合板書直觀理解：腳要增加，兔要增加；腳要增加2，要把1只雞換成1只兔。

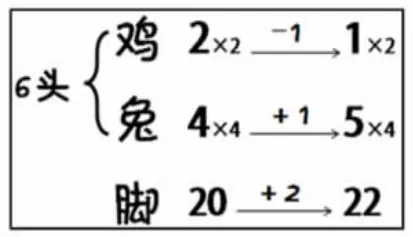
5.回顧方法：先任意猜一個，如果沒猜對，可以根據腳的數量進行調整（板書：猜—調整）。

6.改變腳的數量，學生自己調整：把黑板上的正確腳數“22”改成“16”。

（1）請學生學著板書的樣子寫一寫，并獨立調整出正確的結果。

（2）反饋學生的調整。

水平一：1只1只調整（這種方法同樣予以肯定）。

水平二：一次性調整到位，重點理解“4÷2=2”的道理。

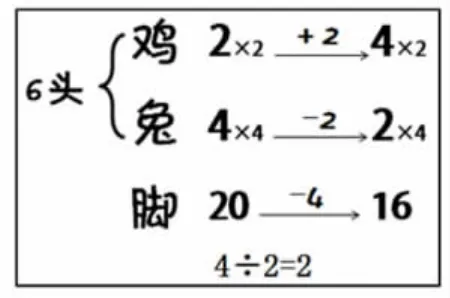
【設計意圖：這個環節是教學的重點，要讓學生初步認識“猜—調整”的方法。這里不必強求學生一定要掌握“一次性調整到位”的方法，而是只要學生能感受到“猜”也能解決問題，并且允許學生1只1只調整。同時，在學生獨立調整的過程中，熟悉“圖式化”的書寫方式。】

三、運用“猜—調整”，加深對方法的理解

1.課件呈現問題：雞兔同籠,從上面數，有12個頭，從下面數，有30只腳。則籠子里有幾只雞？幾只兔？

2.簡單回顧“猜—調整”的方法，然后請學生獨立解決問題。

3.反饋學生的方法。

方法一：先任意猜一個，然后幾次調整找到答案。

請學生解釋自己的思考過程，這樣的方法，重點說明第一次猜好后該往哪個方向調整。

方法二：先任意猜一個，然后一次調整找到答案。

請學生解釋自己的思考過程，這樣的方法，重點說明如何一下子知道要調整幾次。這里，根據學生第一次猜的情況不一樣，可多反饋幾個，加深對“一次性調整到位”的理解。

方法三：假設全是雞或全是兔。

（1）展示學生的算式（或寫到黑板上）。

（2）請學生介紹自己的方法。

（3）思考：他這樣的方法與我們剛才的方法有聯系嗎？（看情況可請學生再解釋一遍）

（4）結合上面的思考，引領全班學生依次理解每個算式的意思（黑板上配合圖示）。

解釋第一步：全部猜成雞或兔，計算出腳的總量。

解釋第二步：與正確腳數量進行比較，得出腳多了或少了的數量。

解釋第三步：根據換一次相差2只腳，得出應該換幾次。

（5）將其納入“猜——調整”方法的范疇，認識到這只是一種猜的比較特殊的方法，全部猜成雞或兔。

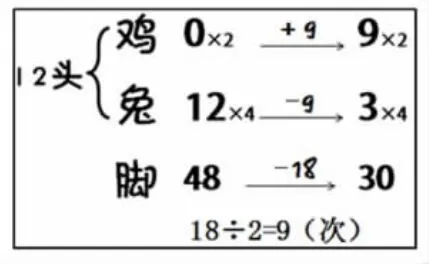
【設計意圖：在這個環節，重點放在猜好以后如何調整的教學上，并將一般意義上的“假設法”納入其中，一方面使本來就會“假設法”的學生有一個展示的機會，同時也使大家理解了這種方法的本質就是“猜—調整”。】

三、多層次練習，鞏固方法

1.專項練習。

課件出示：雞兔同籠,從上面數，有16個頭。從下面數，有40只腳。雞有幾只？兔有幾只？

小明猜：雞可能有8只，兔也可能有8只。

（1）他猜得對嗎？

（2）你能幫他調整嗎？

2.基礎練習。

（1）先出示《孫子算經》中的問題（如圖所示），解釋其意義，再用現代形式表述。

（2）請學生獨立解決。

（3）反饋：重點說清先怎么猜，然后怎么調整。

3.方法推廣。

（1）先出示問題（如圖所示），理解題意。

（2）請學生獨立解決。

（3）反饋：重點在方法推廣與模型建立。

【設計意圖：通過三個層次的練習，旨在鞏固學生對于本課核心方法“猜—調整”的理解和掌握。在練習一和練習二的教學中，可適當滲透“第一次如何猜”的教學，即先各猜一半。練習三重點在模型的建立。】

【課后思考】

通過對不同地方（城鎮、農村等）學校學生調查發現，就“雞兔同籠”解題方法而言，學生的課前知曉率差異是明顯的。有的班級“假設法”的知曉率在10%左右，也有知曉率高于50%的班級。面對這樣的現狀，我們更加堅信“猜——調整”這種方法的普適性。因為，我們的教育，面對的是所有的學生。他們經歷了40分鐘，帶著樸實的“猜”走出課堂，何嘗不是一種成功。

四年級的學生，從不將“猜”看作是一種方法的存在。有一次，老師問學生“猜”這種方法怎么樣？學生都表示這種方法水平太低了。讓學生猜，學生竟然不敢猜。是呀！在他們之前的學習中，都是通過嚴密的計算來尋求問題答案的。當然，本課的“猜”有別于一般意義上的“猜”，其本質是一種假設，這對四年級的學生來說，在認知上是一次飛躍。