求實　求聯　求發展
——《混合運算的復習》教學與反思

莊麗君

復習課一直是教師教學研究的難點所在，很多教師對復習課的目標定位總是落在“鞏固技能”和“熟練掌握”上，容易把復習課變成“炒冷飯”，讓學生在反復操練中重復舊知。其實，復習課不光是對知識的回顧和鞏固，也是把知識“串成知識鏈”的過程——通過復習，使學生理順知識與知識之間的關系，站在高處建構知識結構的大框架。同時，我們還應以復習的知識內容為載體，拓展更多過程性的學習目標，如復習方法的積累、數學思維的鍛煉等。

《混合運算的復習》是二年級下冊的一節單元復習課，作為第一學段的復習課，目標定位上又該如何把握，課型上又該如何處理？筆者進行了實踐研究。

【前測與分析】

復習課的內容是學過的知識，前測更有助于了解學情。本課前測安排了一組遞等式計算：

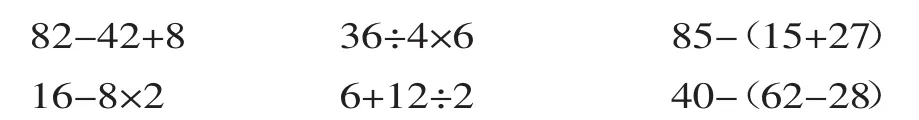
本次前測，共安排了5個班級，各班前測情況比較相似，具體分析如下：

1.正確率高。各班最多有5位學生出錯，最少有3位學生出錯。

?

2.錯誤集中。主要有以下兩種：

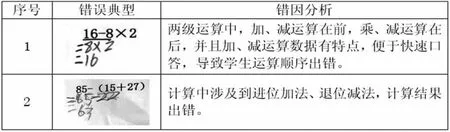
通過這組數據，我認為這節復習課，知識與技能層面的復習目標可以適當弱化，應把教學重心更多地傾向于知識結構的完善以及數學思維的拓展。

【實踐與反思】

一、引導看書，梳理知識，形成結構

1.瀏覽書本，回顧知識。

課件出示四個例題圖，提出看書要求。

師：這是第五單元的學習內容，從第47頁到第58頁，共4個例題。今天復習就從看書開始。

師：誰原意和大家來說一說每個例題我們都學了什么？

學生逐一介紹例題，教師適時小結，形成板書：

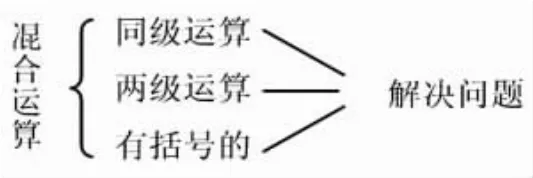
2.交流補充，梳理法則。

師：現在咱們不看書本，能說一說兩步混合運算的運算順序是什么樣的嗎？同桌之間互相說一說，有困難時可以翻看書本。

總結提煉：同級運算，要從左往右按順序計算，不同級運算計算時先算乘除法，后算加減法，有括號的算式要先算括號里面的。

【反思：混合運算這一單元的知識脈絡非常清晰，每個例題的學習內容很明確，因此我通過讓學生翻書看例題回顧所學知識，梳理兩步混合運算的計算法則。這樣的處理，不僅使學生整體把握這一單元的知識，也使學生初步經歷看書復習的過程，體會看書也是其中一種很好的復習方法。】

二、關注前測，查漏補缺，鞏固知識

1.前測錯題分析。

師：上課前，老師還給同學們做了一次前測，還有印象嗎？同學們做得很棒，可惜啊，還是有幾位同學出了一點小問題，咱們一起來看一看。

反饋前測錯誤典型（如下圖）：

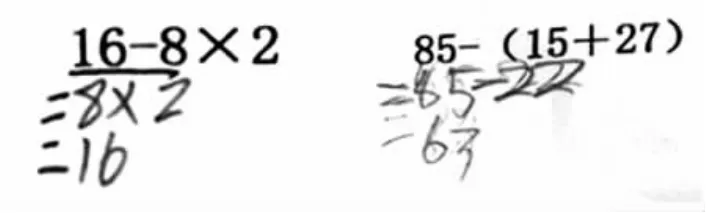
（1）計算順序錯誤。

（2）計算出錯。

每種錯誤典型呈現后，指名錯誤學生自我分析或他人作業點評。

2.小結計算注意點。

師：現在你們覺得像這樣的混合運算，在計算時要提醒大家注意什么？

生：要看清楚第一步算什么再計算；計算時要細心，書寫要干凈清楚……

3.專項練習。

要求：根據老師給出的算式快速算出第一步的得數。

42＋30－15，6＋2×7,2×（7－3），35÷7－2,14－6?2

重點反饋第 5題：14－6?2

（1）學生無法判斷第一步的得數。

師：為什么無法判斷？

生：因為小花遮住了后面的符號。

（2）思考：如果先算14－6，小花后面可能是什么運算符號，如果先算后面一步呢，又該怎么填？

（3）小結：看來小花后面的符號不一樣，它的運算順序就可能不一樣。

4.易錯題題組計算。

【反思：前測練習不光是對學生課前知識能力的檢測，前測的具體情況更是我們學習的素材和資源。因此課中，我把學生的典型錯誤放大，讓學生發現錯誤、分析錯因，然后再進行針對性的題組鞏固、易錯題練習，幫助學生減少錯誤，提高正確率。其中專項練習的最后一題我安排了14－6?2這樣的習題，學生報不出第一步是什么，我抓住契機詢問原因，并引導學生思考如果先算14－6，小花里該怎么填符號，如果先算后面的算式又該怎么填，使學生更靈活地運用混合運算的運算順序進行思考判定。】

三、多層練習，算用結合，拓展思維

1.巧用易錯題，溝通算式聯系。

易錯題安排了5題：

14－6－2、3＋5×9、14－（6＋2）、35＋14÷7、70－（22＋18）

獨立完成并板演校對。

提問：看看第一題和第三題，你還有沒有發現什么奧妙之處呢？

生1：兩題得數相同。

生2：第一題14減6又減2，第三題把6和2先合起來再減，其實是一樣的。

課件利用直觀圖幫助理解：

小結：是的，連續減兩個數，其實就等于減這兩個數的和。

2.變式練習——選擇題。

（1）下面算式先算5－2的是（ ）。

A.5－2＋3B.3×5－2C.5 －(2＋1)

（2）第（ ）組中的兩道題計算結果不一樣。

A.45－14－18 和 45－（14＋18）

B.12÷2÷3 和 12÷（2×3）

C.35－23＋18 和 35－（23＋18）

（3）根據下圖，列出的綜合算式正確的是（ ）。

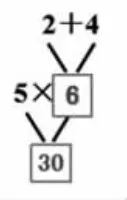
A.5×2＋4

B.（2＋4）×5

C.5×（2＋4）

3.用綜合算式解決問題。

【反思：復習環節的練習，我想不僅要重基礎，還應有所提高和拓展。所以在設計本課時，不少細節處我都精心設計。如5道易錯題計算之后，我讓學生發現 14－6－2 與 14－（6＋2）之間的聯系，借助直觀圖幫助理解算理，明白它們為什么得數相同，初步感受連減的性質；再如變式練習，通過選擇題的形式使學生能綜合運用本課知識快速、準確地做出判斷，提高學生變式思考的能力；最后的解決問題，不僅要求能正確列式，還鼓勵學生用綜合算式思考和解決問題，提升學生用數學概括思考的能力。】