體驗　遷移　探究　創造
——《十進制計數法》教學案例

華麗英

【教學內容】

浙教版四年級。

【教學過程】

一、創設情境，喚醒舊知

1．復習萬以內的數。

（出示三個萬以內的數，一起讀數）

師：這個五位數“21196”是怎么組成的？

生：由2個萬1個千1個百9個十6個一組成。

師：我們把“個位、十位、百位、千位、萬位”叫作數位，把數位上表示的“個、十、百、千、萬”叫作計數單位。

2．初識比萬大的數。

師：生活中還有很多比萬大的數，你能順利讀出這些數么？

師：不太會讀，沒關系。其實這里藏著更大的計數單位和更復雜的數位，今天我們就來研究這些比萬更大的數。

【評析：萬以內數的認識是學習十進制計數法的基礎，也是重點。通過復習，喚醒學生已有的知識經驗，為遷移拓展學習新知識做好準備。同時拋出使學生產生認知沖突的問題情境，促進學生積極思考。】

二、經歷探索，構建新知

1．表征十萬。

師：這是一輛國產普通轎車，猜一猜，售價多少？老師告訴你們，這1捆表示1個1萬，請你數一數。

生：1個1萬，2個 1萬，3個1萬……9個1萬。

師：還有1捆。

生：10個1萬。

師：現在是1個——，10個一萬就是1個——。

生：十萬。

生：10個一萬就是 1個十萬。

師：請你用自己的方法把十萬表示出來。

（1）多元表征。

想：怎樣表示10萬；寫（畫）；說：同桌交流。

（2）展示匯報。

①畫圖。

○10000

○○○○○○○○○○100000

生：1個圓代表1萬，10個圓就是10萬。

②算式。

10×10000=100000

生：10乘10000就是十個一萬，是十萬。

③100000。

師：直接用數字表示，可以嗎？數一數，十萬后面跟著幾個0？

④計數器。

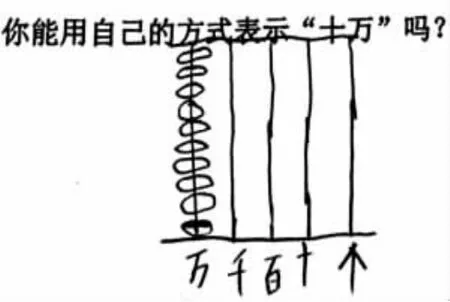
生：萬位上一顆珠子表示一萬，10顆珠子就表示10個一萬，10個一萬就是十萬。

（3）創造單位。

師：如果只有1顆珠子，怎么在計數器上表示出10萬？

（出示學生作品）

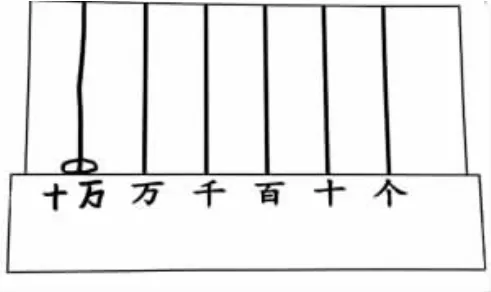
師：你是怎么想的？

生：畫一個十萬的計數單位，在十萬上畫1顆珠子。1個十萬就是十萬。

師：他又創造了一個新的計數單位“十萬”，在十萬上畫1顆珠子，就表示1個十萬。

師：我們一起來數一數，1個1萬，2個1萬……9個1，萬數到10個1萬。

（學生在十萬上撥1顆珠子）

師：看來10個一萬就是1個十萬。數學上十萬不僅表示一個數，也表示一個計數單位。

【評析：在學生的頭腦中，認為比“萬”大的計數單位就是“億”，把“十萬”從數提煉成一個“復合式”計數單位是本節課的重點和難點。在學生原有的認知結構中，“十萬”作為一個數是很容易理解的，但“十萬”作為一個計數單位，學生沒有經驗，也缺乏這樣的認知準備。怎樣使“量的積累”達到“質的飛躍”，使一個“數”凝聚成一個“計數單位”？如何在這樣一個概念教學中體現高階思維？探究創造必不可少。讓學生經歷多元表征和解讀，創造出“十萬”這個“復合式”計數單位。學生的表征方式多樣：用文字表征、畫圖表征、算式表征、簡易計數器表征。這個過程使得學生對“新”的計數單位——“十萬”有了深度體驗，這也是基于對原有經驗、原有認知的成功拓展。】

2．認識更大的計數單位（百萬、千萬）。

師：如果繼續這樣數，是不是還有新的計數單位產生呢？

師：我們來撥一撥，數一數。

認識百萬：7個十萬、8個十萬、9個十萬、10個十萬（1個百萬）。

認識千萬：8個百萬、9個百萬、10個百萬（1個千萬）。

3．討論為什么定義“億”。

認識億：9個千萬，10個千萬（1個億）。

生：億。

師：你們又創造了一個新的計數單位。除了“億”，10個千萬還有不同的命名嗎？

生：萬萬。

師：你是怎么想的？

生：10個千是萬，10個千萬就是萬萬。

師：這樣的確也很通俗易懂。難怪有人也用萬萬來表示呢！

師：那到底是萬萬合適還是億合適呢？

生：億比較簡單方便。

生：萬萬更容易理解它的意義。

師：其實數學的命名有它自身的需要。如果用萬萬來命名，往上數就是十萬萬、百萬萬、千萬萬、萬萬萬……一直一直數下去，那計數單位的字就越來越多了。所以數學上規定10個千萬是1億。

師：萬、十萬、百萬、千萬都是用萬來命名的，再往上又有了新的計數單位“億”。再往上數，就會有——

生：十億、百億、千億。

【評析：億和萬萬這兩個單位是等價的。“萬萬”從邏輯推理上說，產生合情合理。可是數學上卻規定“一萬個萬”的計數單位是“億”，學生在矛盾沖突中通過數數，體會計數單位的簡潔性，體驗數學發展由繁到簡的自身需要。同時學生經歷正向遷移，以十萬為計數單位進行計數，從十萬拓展出百萬、千萬、億、十億、百億、千億，充分感知到比萬大的數不僅僅是億，還有十萬、百萬、千萬等等。】

4．整理數位順序表。

師：能不能把從“個”到“千億”這些計數單位排排序？

（1）按順序排序。

學生排序，尋找計數單位之間的規律并思考可以快速記憶計數單位的方法。

（2）展示匯報。

（選取兩種不同順序的作品進行展示）

師：一種是從小到大的順序，一種是從大到小的順序。如果從讀數的角度講，這些計數單位怎么排比較好？

生：從大到小比較好，數位順序表是從右邊看起，小的在右邊，大的在左邊。

師：我們從右起，規定計數單位分別是個、十、百……

（3）發現規律。

師：觀察計數單位之間有什么規律？

①十進制。

生：相鄰兩個計數單位之間的進率都是十。

師：你能舉個例子嗎？借助小立方體解釋十進制。

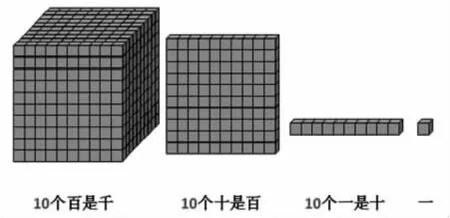
生：每相鄰兩個計數單位間的進率都是十，這樣的計數方法叫做十進制計數法。

②四位一級。

師：你有什么好辦法可以快速地記住這么多計數單位？

生：個、十、百、千，然后萬、十萬、百萬、千萬，再往后是億、十億、百億、千億。

生：我們可以把個、十、百、千看成是一組，萬、十萬、百萬、千萬看成是一組，億、十億、百億、千億看成是一組。

師：真的是這樣嗎？

（出示小立方體，在學生發現特征后進行解釋）

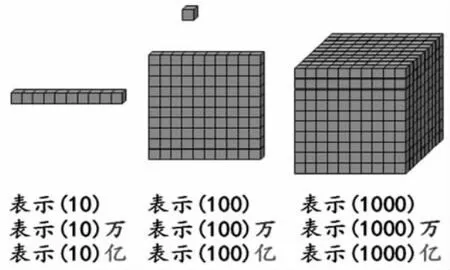
師：為什么同樣的圖，表示的數卻不一樣？

生：因為1個小立方體表示的大小不一樣。

師：通常我們將四位數位分為一組，這些帶有萬字的為一組，帶有億字的為一組。每一組都有一個級別，分別是個級，表示幾個一；萬級，表示幾個萬；億級，表示幾個億。像個級、萬級、億級稱為“數級”，當然還有很多更大的數級。

（4）完善數位順序表。

師：我們認識了新的計數單位，還知道了數位、數級，這就形成了一張完整的整數數位順序表。請你用我們剛才找到的好辦法，快速地記一記。

師：從個位起，第五位是什么數位？第九位呢？千萬位在從右起的第幾位？

師：你怎么這么快就知道了呢？有什么秘訣？

生：四個數位為一級，第九位是億級第一個，所以是億位。

生：千萬位是萬級最后一個，所以2×4=8，它在第八位。

（5）認識意義。

結合課件，出示一個多位數：748329046，思考：這是一個（）位數，最高位是（）位，是由（）個億（）個萬和（）個一組成。

師：你們是怎么知道它是由7個億，4832個萬，9046個一組成的？

生：因為我們剛才學了四位一級，它億級上只有7，所以是7個億，萬級上有4832，所以是4832個萬，個級上是9046，所以就是9046個一。

師：這是根據數級來理解它的意義的。

師：2個4表示的意義一樣嗎？為什么？

生：右邊的4表示4個十，左邊的4表示4個千萬。

師：說明不同的數位表示不同的意義。

【評析：學生對計數單位的排序有從小到大，也有從大到小。結合讀數，比較、感受計數單位從大到小排序的合理性。同時對計數單位進行觀察，發現每相鄰兩個計數單位之間的進率都是十。通過數形結合加深對十進制的理解，感悟十進制思想；通過對數位分級的理解，自我構建完整的整數數位順序表。學生經歷擴展、排序、分級等數學活動，逐步形成關于自然數的整體認知結構。學習是學習者自主建構知識的過程，是學生從原有經驗出發，不斷組織原有經驗，使之結構化，進而形成新的知識和經驗。】

三、應用拓展，回顧整理

1．交流自己收集的大數。

師：請將自己收集的大數分分級，說說它是一個幾位數。

（1）尋找特殊數之間的聯系。

師：最大八位數與最小九位數之間的關系。

（2）感受億的大小。

知道一個數的大小是要在具體的情境中感悟的。

2．回顧整理。

師：這節課你有什么收獲？想一想，我們是怎么學習的？

師：我們認識了大數的數位、計數單位、數級，還知道了分級，那么怎么讀、怎么寫呢？我們下節課再來研究。

【評析：數感是人的一種基本數學素養，是人對數與運算的一般性理解。這種理解可以幫助人們運用靈活的方法作出數學判斷，并為解決復雜的問題提出有用的策略。這一教學內容，恰恰是數感培養的重要載體。但是它又是數學的一種規定，那么學生在課堂中可以探索嗎？值得探索嗎？這節課立足培養學生的高階思維，把握每一個教學內容中蘊含的思維元素，引導學生從記憶到理解，從規定到創造，是一種新的探索與嘗試。】