基于改進的非線性GM(1,1)模型的職業病預測研究*

楊　珊，明俊樺，周智勇

(中南大學 資源與安全工程學院，湖南 長沙 410083)

0　引言

據國際勞工組織(ILO)資料顯示，全球范圍每年有接近2百萬人死于職業相關疾病。因職業傷害引起的世界經濟損失達到2.8萬億美元，在全球各國國民生產總值中占據4%[1]。喬慶梅、徐金梅[2-3]指出，目前我國職業病狀況不容小視，與職業病有關的相關參數都占全球第一。因此，職業病的預防形勢相當嚴峻。朱進平、梅震[4]的研究表明，職業病具有遲發性和隱匿性，未來的病例數也會逐漸增加。關于職業病研究方面，國內外已有較多學者參與，相關研究成果也已在職業病預防措施中得到應用。例如：孫銀鈴、邵華等[5]指出，從整體上來說，中國在職業病防治方面的力度與美國有一定差距，還有很多工作要做；日本的恒川謙司[6]在了解中國職業衛生的現狀基礎上，結合日本的職業衛生措施，提出一系列建立、健全中國職業衛生管理的對策和建議。但是，針對全國范圍內的職業病預測，現有研究尚有不足，灰色預測方法以其所需樣本小、建模簡單、精度高及實用性強等特點，得到廣泛應用[7-8]。王維、李建東[9]使用經典GM(1,1)模型，對職業病分類進行了預測分析，相關預測準確度尚不夠理想；李怡、張華東[10]雖然使用的是改進GM(1,1)模型，不過并沒考慮到非線性關系；文獻[11]和[12]提到了非線性GM(1,1)改進模型，其應用的領域分別是房地產價格指數預測以及“兩稅”稅收預測，為本文提供了一定的理論基礎，不過該方法的預測精度仍有提高空間；時冬青、宋文華等[13]提出灰色 GM(1,1)—馬爾科夫模型，將其應用在職業病預測方面。在現有學者相關職業病預測方面的研究成果基礎上，本文進一步完善和改進相關預測模型，提出改進的非線性GM(1,1)改進模型，為職業病發病趨勢的預測提供理論和方法參考。

1　經典GM(1,1)模型

將原始數據記為序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),經典GM(1,1)模型建模步驟如下：

1)步驟1，對原始序列X(0)做一次累加生成，得數據序列：

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(1)

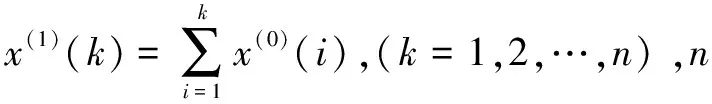
2)步驟2，建立GM(1,1)模型的基本形式，如式(2)所示：

x(0)(k)+az(1)(k)=b,k=1,2,…,n

(2)

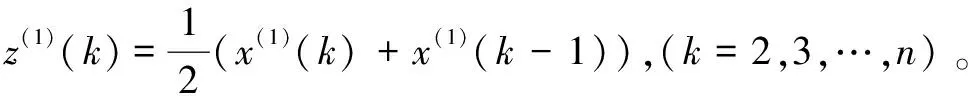
(3)

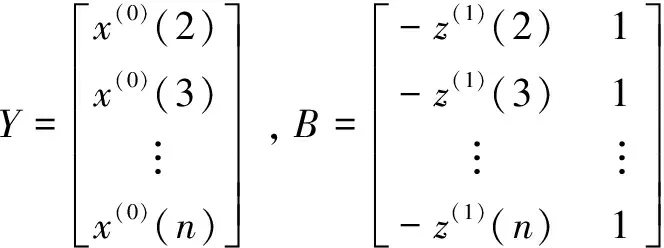
4)步驟4，模型(2)對應的白化方程或影子方程為：

(4)

由其解得時間響應函數：

(5)

取x(1)(1)=x(0)(1)，則模型(2)的時間響應序列為:

(6)

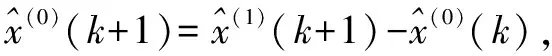
(7)

2　改進的非線性GM(1,1)模型

因國家政策、社會條件等因素的影響，歷年實際職業病例數規律性相對較弱，其增減趨勢不一，會出現陡增或陡減的現象，因此本文首先選用幾何弱化算子理論對原始數據進行處理，使數據變得有規律可循，增強模型預測的準確度。

由式(2)可知，經典的GM(1,1)模型實質上是把{x(0)(k)}和{z(1)(k)}這2組數值之間看作線性關系進行求解參數的。但是，在實際計算過程中，{z(1)(k),x(0)(k)}的散點往往不在一條直線上，即不符合線性關系，若仍做線性關系進行處理，就會造成較大的誤差。因此，改進模型將{z(1)(k),x(0)(k)}原本的線性假設，改為非線性假設進行處理，以提高曲線的擬合度。

為保證方程的可解性，本文將結合常用曲線(直線：y=a+bx；雙曲線：1/y=a+b/x；冪函數曲線：y=b0xb1；指數函數曲線：y=b0eb1x；增長曲線：y=eb0+b1x)建立非線性方程，再比較各曲線的擬合度，找到最吻合的曲線關系，分析曲線參數，最終得到非線性GM(1,1)模型。相關分析步驟如下所示：

1)步驟1，利用幾何平均弱化緩沖算子，對原始數據進行處理。設X(0)=(x(0)(1),x(0)(2),…,x(0)(n))為非負的系統行為數據序列，即x(0)(i)≥0。令

X(0)′ =X(0)D= (x(0)(1)d,x(0)(2)d,…,x(0)(n)d)

(8)

其中：

2)步驟2，分別將數據從上述曲線出發，建立非線性回歸模型：

x(0)(k)=fi(z(1)(k),a,b)i=1,2,…,6

(9)

式中：a,b為未知參數。

3)步驟3，基于R2最大原則，確定最佳擬合曲線f(z(1)(k),a,b)。其中R2是表示各曲線與原始數據的擬合程度的參數，其數值越大，則代表曲線的模擬值和原始數值的差別越小，則該曲線的模擬效果越好。

4)步驟4，預測精度的檢驗，通過后驗差比值C和小誤差概率P，評判模型預測精度的合格與否[13],如表1所示，其計算公式分別為：

(10)

P=P{|ε(t)-ε| <0.674 5s1}

(11)

式中：s2為殘差數列的標準差，s1為原始數列的標準差，ε(t)為殘差數列，ε為殘差數列均值。

3　應用實例

本文用我國職業病發病例數作為研究對象，驗證該改進的非線性GM(1,1)模型的可靠性和準確性，使用2005—2014年的數據作為研究數據，資料來源于2005—2014年國家衛生和計劃生育委員會(衛生部)發布的關于職業病防治情況的通報[13]，具體數據如表2所示。

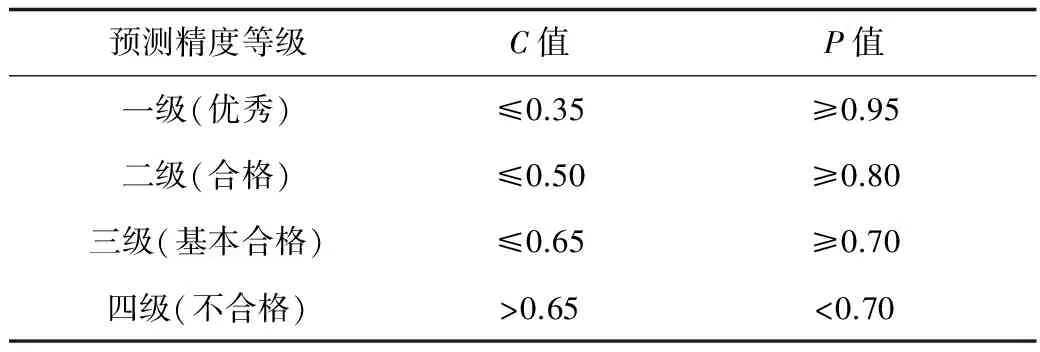
表1　后驗差比值和小誤差概率預測精度評判檢驗

表2　2005—2014年我國職業病發病例數統計

其中，2006年的職業病例數為29個省份的數據，其他年份均為30個省份的職業病數據，因此，為了使數據具有較高的參考性，本文利用“平均值比例差補法”[13]，以 2005 年的職業病發病例數作為依據，算出2006年的數據為11 805例。

3.1　傳統GM(1,1)模型

以2005—2013年的9個職業病例數為建模數據進行處理。設：

X(0)=(x(0)(1),x(0)(2),x(0)(3),x(0)(4),x(0)(5)，x(0)(6)，x(0)(7)，x(0)(8)，x(0)(9))=(12 212.00,11 805.00,14 296.00,13 744.00,18 128.00,27 240.00,29 879.00,27 420.00,26 393.00)

采用傳統GM(1,1)模型進行擬合，得到結果如表3所示。

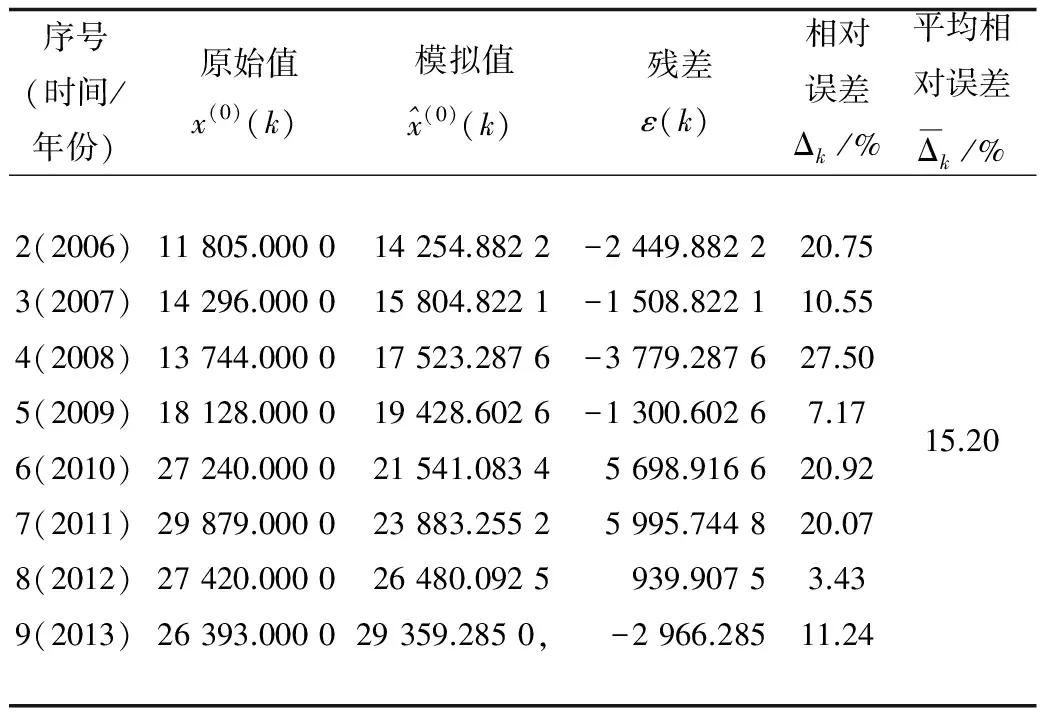
表3　傳統GM(1,1)模型的建模擬合效果

由表3可以看出，傳統GM(1,1)模型擬合的平均相對誤差為15.20%，并預測得到2014年的職業病例數為32 552例，根據職業衛生網的數據，2014年的職業病例數為29 972例[13]，預測相對誤差為8.61%。由此可知，該經典模型預測誤差較大。

3.2　改進的非線性GM(1,1)模型

3.2.1幾何平均弱化緩沖算子的應用

2005—2013年的數據并不是呈現穩定增長或減少的狀態，會受到各種因素的影響而波動較大，特別是2010年的數據陡增。如果直接利用原始數據進行模型的構建，那么預測結果很大程度上不具備參考性。針對這個問題，灰色系統中提出了“灰色序列”，主要通過對原始數據的挖掘以及整理，重新發現數據之間的規律，進而構建數量關系模型。從表2可以看出，2010年的職業病的病例數陡增，因此采用幾何平均弱化緩沖算子對原始數據進行處理，減緩其增長速度[14]。處理過程如下：由式(8)計算得到弱化值X(0)′ = (18 812.451 4,19 856.500 7, 21 462.816 2, 22 966.707 3,25 450.472 7, 27 703.353 4, 27 859.549 5, 26 901.599 6, 26 393.000 0)。

3.2.2改進的非線性GM(1,1)模型的建模

采用SPSS軟件，選取幾種常見的曲線模型進行分析，表4給出了各個曲線模型的擬合優度、模型檢驗結果和參數估計值。由R2最大原則，確定最佳擬合曲線。其中二次曲線模型的R2=0.966，該模型的擬合度最佳。幾種曲線模型的擬合效果如圖1所示，小圓圈代表原始觀測記錄，從直觀上看，顯然二次曲線和原始數據擬合的更好。

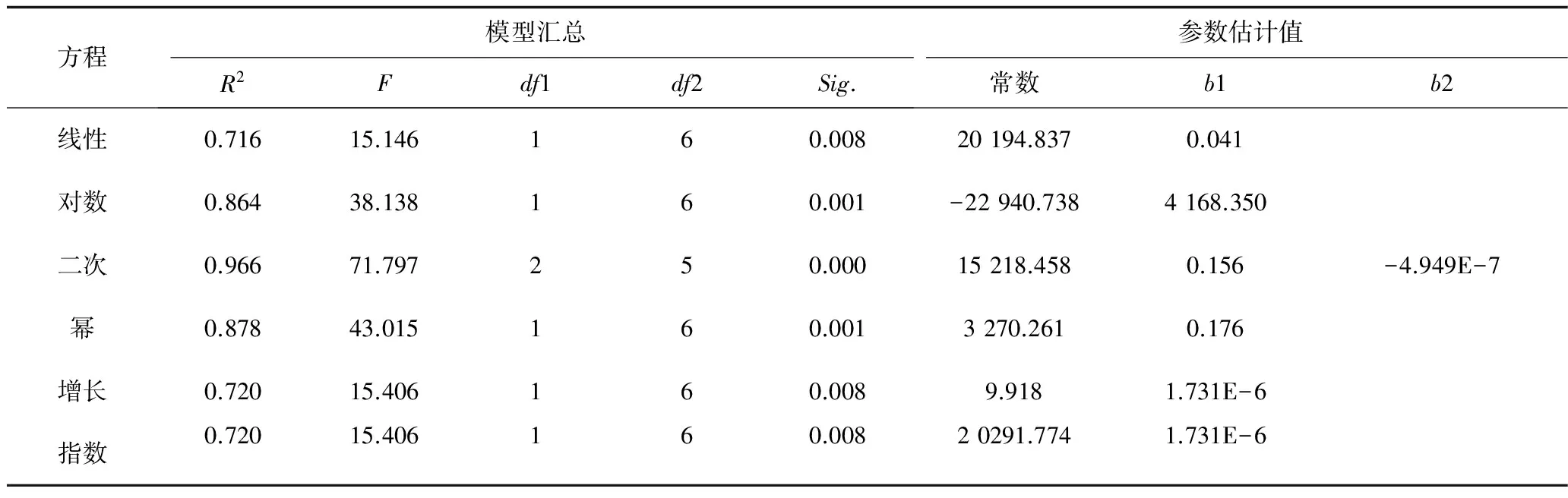
表4　常見曲線模型匯總和參數估計值

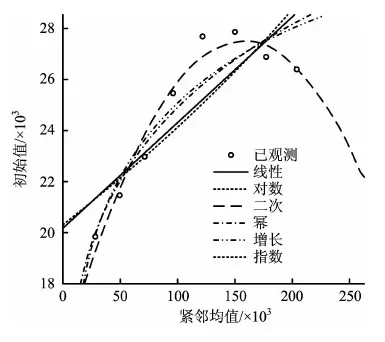
圖1　常見曲線模型擬合效果Fig.1　Fitting effect of common curve model

二次曲線的方程設為：y=ax2+bx+c。以數列X(0)′作為因變量y值，而該數列的緊鄰均值作為自變量x值，利用MATLAB計算出二次曲線的參數a，b，c，得到所求二次曲線的方程為：

y=-4.949×10-7x2+0.156x+15 218

(12)

將X(0)′的緊鄰均值數列作為自變量帶入式(12)中，可求得相應的因變量，即擬合值，詳見表5所示。從表5可知，改進的非線性GM(1,1)模型的擬合值和原始值之間的平均相對誤差為1.81%，低于傳統GM(1,1)模型的平均相對誤差。接著利用該模型，重復上述步驟重新建模，預測得到2014年的職業病例數為29 042例，根據職業衛生網的數據，2014年的職業病例數為29 972例，預測相對誤差為3.10%，比經典GM(1,1)模型的預測精度高。

3.2.3擬合效果比較

利用后驗差比值C和小誤差概率P這2個參數指標來比較2種模型的預測精度，如表6所示。

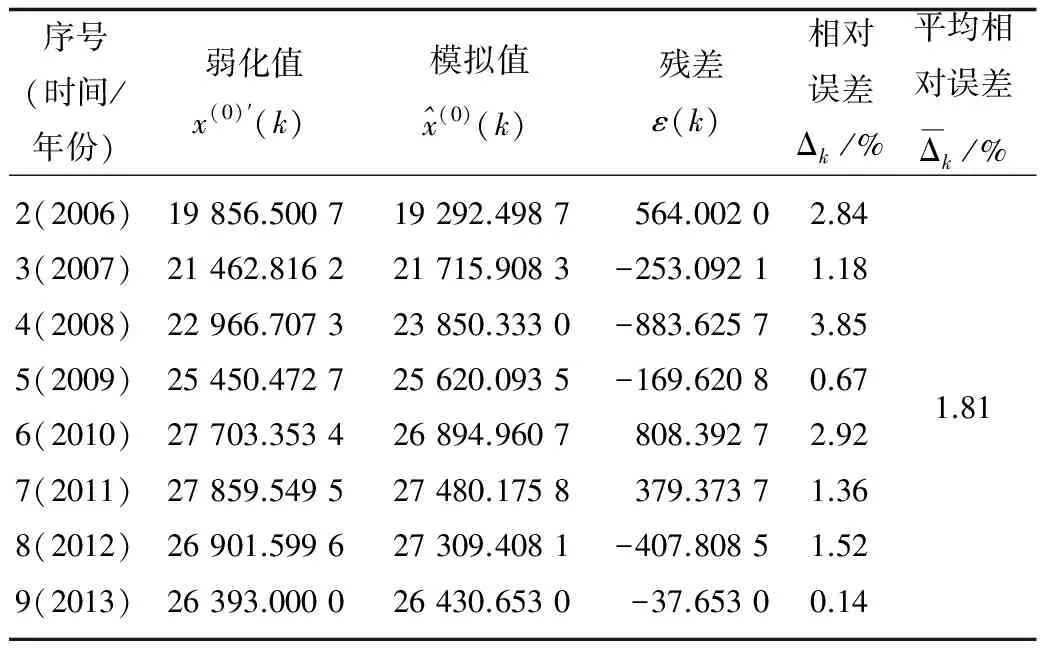
表5　改進的非線性GM(1,1)模型的建模擬合效果

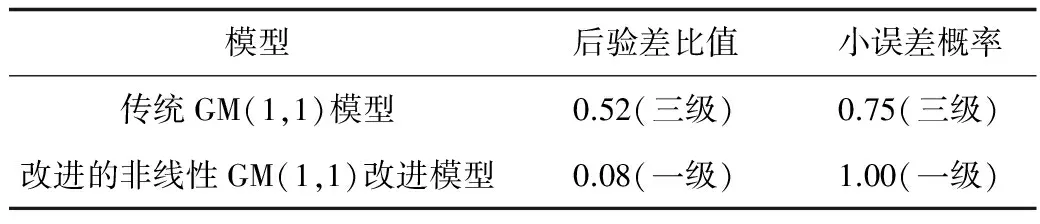
表6　2種模型的預測精度比較

從表6中可以看出，改進的非線性GM(1,1)模型的預測精度比傳統GM(1,1)模型高，可為職業病預測以及職業衛生防治措施等工作提供更準確的參考和支持。

由表3和表5數據可分別得到傳統GM(1,1)模型的擬合曲線效果圖和經弱化處理的非線性GM(1,1)改進模型的擬合曲線效果圖，如圖2和圖3所示。

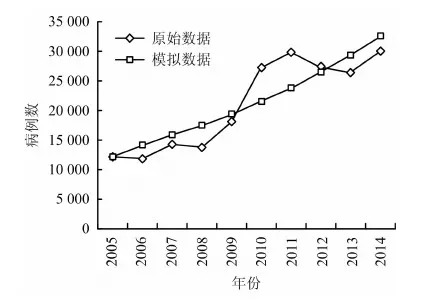
圖2　傳統GM(1,1)模型的擬合效果Fig.2　The fitting effect diagram of the traditional GM (1,1) model

圖3　改進的非線性GM(1,1)模型的擬合效果Fig.3　The fitting effect diagram of the improved GM (1,1) model

由圖2可看出，在傳統GM(1,1)模型預測中，原始數據有較大的波動，而得到的模擬數據卻是一條平滑曲線，并未體現出數據的變化特征；由圖3可看出，改進的非線性GM(1,1)模型中的弱化數據和模擬數據基本一致，擬合度較高。可見，改進模型中引入的弱化理論和非線性假設，有效地解決了預測精度不高的問題，為職業病預測提供了有效的方法。根據改進的非線性GM(1,1)模型，進一步預測得到2015年的職業病病例數為34 900例。

4　結論

1)改進的非線性GM(1,1)模型中，利用幾何平均弱化算子對原始數據進行處理，并將原始數據與緊鄰均值之間線性假設變為非線性假設，使得該模型在職業病發病例數的預測精度上有了較大提高。

2)通過比較可知，相比傳統模型的職業病預測平均相對誤差15.20%，改進的非線性模型降低到了1.81%；以2014年為驗證數據時，傳統模型的相對誤差為8.61%，而改進的非線性模型變為3.10%；在后驗差比值和小概率誤差檢驗時，傳統模型的預測精度為三級，而改進的非線性模型提高到一級。

3)根據該改進的非線性GM(1,1)模型，得到2015年職業病的預測值為34 900例。

4)職業病的病例數會受到多種因素的影響，例如其本身所具有的“隱匿性”、“遲發性”等特點，各種診斷儀器及標準的更新，人們思想觀念的轉變等。以上因素在一定程度上，會影響該模型的預測精度，但職業病的總體趨勢依舊在不斷增長，我國仍需加強對職業病的防治力度，盡最大的努力保障最廣大人們群眾的身體健康。

5)今后職業病的預測將會越來越細化，即具體到每一種職業病的發病例數的預測，以便為我國職業病的防治工作提供更有力的支持。

[1]賈麟.全球職業安全健康問題與新形勢[J].中國安全生產,2014(11):58-59.

JIA Lin.Global occupational safety and health issues and the new situation[J].China Occupational Safety and Health, 2014(11):58-59.

[2]喬慶梅, 柯常云. 我國職業病防治的現狀與思考[J]. 中國醫療保險, 2011(12):59-62.

QIAO Qingmei,KE Changyun.The present situation of occupational disease prevention and cure in china and thoughts on it[J].China Health Insurance,2011(12):59-62.

[3]徐金梅．職業病防治現狀分析及其對策[J]．西部探礦工程，2008，20(7)：239-241.

XU Jinmei.The actuality analysis and countermeasure of prevention and cure of industrial disease in China[J]. West-China Exploration Engineering,2008,20(7):239-241.

[4]朱進平，梅震．職業衛生監督量化分級管理模式探討[J]．工業衛生與職業病，2008，34(6)：378-381.

ZHU Jinping,MEI Zhen.Discussion on quantitative classified management mode of occupational health supervision[J].Industrial Health and Occupational Diseases,2008,34(6):378-381.

[5]SUN Y, SHAO H, WANG H. Occupational diseases prevention and control in China: a comparison with the United States[J]. Journal of Public Health, 2015, 23(6):379-386.

[6]恒川謙司, 劉寶龍, 高建明,等. 日本職業衛生管理及對中國的啟示[J]. 中國安全生產科學技術, 2008, 4(1):116-119.

TSUNEKAWA K, LIU Baolong, GAO Jianming，et al. Occupational health management in Japan and its enlightenment to China[J].Journal of Safety Science and Technology,2008,4(1):116-119.

[7]LIN Y, LIU S. An introduction to grey systems: foundations, methodology and applications[J]. Kybernetes, 2003, 32(4):584-585.

[8]劉思峰. 灰色系統理論及其應用(第五版)[M]. 北京：科學出版社, 2010.

[9]王維,李建東.GM(1,1)灰色模型在職業病發病預測中的應用[J].中國公共衛生管理,2014,30(6)：920-922.

WANG Wei，LI Jiandong. Application of GM(1,1) grey model in prediction of occupational disease[J]．Chinese Journal of Public Health Management,2014,30(6): 920-922．

[10]李怡，張華東．改良灰色模型在職業病發病趨勢上預測的分析研究[J]．預防醫學情報雜志，2015，31(8)：630-634.

LI Yi，ZHANG Huadong．Application of refined grey model in forecasting the of occupational disease[J].Journal of Preventive Medicine Information,2015,31(8): 630-634．

[11]錢峰, 呂效國, 朱帆. 灰色GM(1,1)模型的改進模型在房地產價格指數預測中的應用[J]. 數學的實踐與認識, 2009, 39(7):29-33.

QIAN Feng,LYU Xiaoguo,ZHU Fan.The application of the improved grey GM (1,1) model in real estate price index prediction[J].Mathematics in Practice and Theory,2009,39(7):29-33.

[12]郭曉君，李大治，褚海鷗，等．基于GM(1,1)改進模型的“兩稅”稅收預測研究[J]．統計與決策，2014(4)：34-36.

GUO Xioajun,LI Dazhi,CHU Haiou，et al. The study on the prediction of "Two Taxes" tax based on the improved GM(1,1) model[J].Statistics and Decision,2014(4):34-36.

[13]時冬青, 宋文華, 張桂釧,等. 基于灰色GM(1,1)-馬爾科夫模型的職業病預測研究[J]. 中國安全生產科學技術, 2017, 13(4):176-180.

SHI Dongqing,SONG Wenhua,ZHANG Guichuan，et al.Study on prediction of occupational diseases based on grey GM(1,1)- markov model[J]. Journal of Safety Science and Technology, 2017,13(4)：176-180.

[14]陳昌源, 戴冉, 楊婷婷,等. 基于改進 GM(1,1)模型的上海港集裝箱吞吐量預測[J]. 船海工程, 2016, 45(4):153-156.

CHEN Changyuan,DAI Ran,YANG Tingting, et al. Study on container throughput prediction of shanghai port based on improved GM(1,1) model[J].Ship & Ocean Engineerine, 2016, 45(4): 153-156.