復雜構件應變狀態測量的三維DIC技術

朱飛鵬，　江真丞，　白鵬翔，　雷　冬

(河海大學 力學與材料學院，南京 210098)

0　引　言

實際工程測試中，構件應變狀態的測量至關重要，它是構件健康監測的重要依據。目前工程中最廣泛采用的應變狀態測試方法是電阻應變測量方法(簡稱電測法)[1-5]。對于一般的復雜構件而言，使用電測法時，首先需要根據受力分析確定構件上最危險點的所在位置，然后在該點黏貼應變花，得到組成應變花的各單片的應變讀數，再根據實驗應力分析最終確定出該點的應力狀態(主應力大小與主方向)。然而，電測法在使用中存在一些不足：① 需要人為確定構件上危險點的位置，這需要較強的力學功底；② 電測法屬于單點測量方法，所反映出的構件變形信息極為有限；③ 由于應變片測得的應變是其敏感柵區域內的平均應變，故在應力梯度較大的點處所得到的應變與實際情況必然有所差異；④ 測量結果易受應變片黏貼位置、方向及黏貼質量等因素的影響[6]。在之前的研究中，筆者提出多次黏貼單軸應變片的方案[7]，可以提高應力梯度較大點的應變狀態的測量精度，然而該方法的使用需要待測構件在結構上有一定的對稱性，因此不具有通用性。

三維數字圖像相關(三維DIC)方法是一種基于數字圖像處理技術的現代光測力學手段[8]。與傳統的電測法相比，該方法具有非接觸、全場測量的優越性，因此，在科研與工程技術領域得到了越來越廣泛的應用[9-12]。三維DIC通過跟蹤試件變形前后表面散斑的位置變化來計算試件表面各點的位移與應變信息，可一次性獲得某點平面應變的全部3個分量，因此，可以方便地用它來實現上述復雜構件上危險點的應變狀態測量。本文通過一個實例構件的加載試驗來說明三維DIC方法在用于復雜構件應變狀態測量方面的有效性，并將結果與電測法以及有限元分析的結果進行比較，分析三維DIC方法關于應變狀態測量的精度。

1　三維DIC測量原理

Luo等[13]最早提出了基于雙目立體視覺原理和DIC技術的三維DIC方法，通過雙目相機的視差數據和標定數據，重構出被測物表面在變形前后的三維形貌，進而獲得三維位移場和應變場。

1.1　三維形貌測量

雙目立體視覺的原理如圖1(a)所示，由2個互成一定角度的相機拍攝待測物體表面的同一區域。空間中的點P(Xw,Yw,Zw)分別成像于左、右相機平面上的P1(u1,v1)與P2(u2,v2)點。雙目立體視覺通過已標定好的雙相機內、外參數，由點P1(u1,v1)和P2(u2,v2)的圖像坐標來確定空間點P的三維坐標(Xw,Yw,Zw)。相機標定是獲取相機內外參數的過程，左、右相機同時拍攝若干張平面標定板(棋盤格、圓點或同心圓特征圖案)在不同姿態下的圖像，將標定板上特征圖案的精確相對位置作為已知參數，根據非線性最小二乘優化方法來確定系統的內、外參數。

(a)雙目立體視覺

(b)三維位移計算

1.2　位移場和應變場的計算

由雙目立體視覺和DIC方法可確定點P在變形后的三維空間坐標P′。將點P′與P的坐標向量相減即可得到試件表面待測點的三維位移。對圖像中所有像素點重復上述過程，就可求出試件表面的位移場。由于根據DIC算法直接獲取的位移場不可避免會含有一些噪聲，因此，需要對位移場數據進行平滑處理[15]后再作差分計算即可求得待測試件表面的應變場。

2　試驗及過程

2.1　試件與試驗裝置

試驗采用如圖2所示的第十屆全國周培源大學生力學競賽“基礎力學實驗”團體賽的偏心拉伸鋁合金試件作為待測試件，其泊松比υ=0.3，厚度為8 mm，彈性模量E待測。試件加載沿著圖2(a)中的一對孔B、B′作為拉伸方向。為比較測量結果，取圖2(a)中A點(其應力梯度較大)的應變狀態測試為例進行分析說明。

分析表明，用材料力學或是彈性力學都無法求解出A點的應力狀態。根據試件結構的對稱性，在其正、反面共計黏貼5枚應變片，如圖2(b)、(c)所示。其中，1、2、3(0°，45°，90°)號應變片組成45°直角應變花來測得復雜點A的應變狀態；4、5 號應變片(黏貼在關于截面高度對稱位置)用來測量試件的彈性模量。此外，在試件正面待測點區域噴制上隨機分布的散斑。

(a) 試件尺寸(mm)

圖2試件及應變片黏貼位置

圖3(a)為試驗中采用的三維DIC變形測量系統，主要由2個數字相機組成，每個相機由一個CCD圖像傳感器(Point Grey, GRAS-50S5C-M, Canada)和一個23 mm的定焦鏡頭(Schneider Xenoplan 1.4/23)構成，將這2個相機固定在同一個三腳架上。加載設備為INSTRON 3367電子萬能試驗機。

(a)試驗測試裝置(b)試件實物圖

圖3電子萬能試驗機及三維DIC測試系統

2.2　試驗過程

將試件夾持在試驗機的上下夾頭之間，如圖3(b)所示。首先需要測定試件材料的彈性模量，采用測試過程如下：試驗開始前，施加200 N作為初始荷載，這時將應變儀讀數清零；然后使用逐級等量的加載方式，每級增量為200 N，分8級加載。在每個加載點，記錄下應變片4、5的讀數。

測試完彈性模量之后，開始應變狀態的測量試驗，具體過程如下：試驗前，給試件施加200 N作為初始荷載，這時采集一組圖像作為參考圖像；然后使用逐級等量的加載方式，每級增量為500 N，分4級加載。在每個加載點，控制三維DIC系統采集一組變形圖像，同時記錄應變片1、2、3的讀數。

3　試驗結果分析

3.1　彈性模量測試結果

在圖2(a)所示的試件B、B’處施加一對作用力使其發生偏心拉伸時，分析可知應變片4、5所在截面為拉伸、彎曲組合變形，因此其應力可寫成如下形式：

(1)

式中：FN、Mz為截面軸力和彎矩；y為應變片敏感柵中點到截面中性軸的距離。將應變片4、5的應力取均值，便可消除彎矩的影響，得到軸向應力σ=FN/A。再將測得的應變片4、5的應變取均值，得到軸向應力引起的拉伸應變，根據單向應力狀態下的胡克定律E=σ/ε，可得出彈性模量的數值。

表1為試驗中記錄下的4、5號應變片讀數。為減小試驗過程中的測試誤差，試驗重復3次。從表中可知，由于偏心拉伸作用，使得5號應變片讀數為負，說明彎矩產生的彎曲拉應變大于軸向拉伸正應變。根據表1的3組應變—荷載數據，經過擬合得到3次彈性模量的平均值為71.0 GPa。

表1　3次重復加載下的4、5號應變片的讀數

3.2　電測法測得的A點應變狀態

根據材料力學平面應變狀態分析，已知某測點直角應變花3個方向的應變ε0°、ε45°、ε90°，則其主應變大小為：

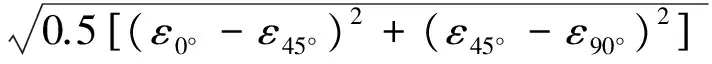
(2)

3次重復加載試驗中得到直角應變花(1、2、3號應變片)的應變數值如表2所示。將這3組數據分別代入式(2)，計算得出3次試驗中試件上A點主應變大小，如表3所示。

表2　電測法測得的應變花的應變數值

表3　電測法測得的主應變大小

3.3　三維DIC法測得的A點應變狀態

將試驗中采集到的200 N時的試件圖像作為參考圖像，計算0.7、1.2、1.7、2.2 kN荷載下的全場變形，分別得到4個荷載狀態下的全場主應變。

圖4為荷載增量為2.0 kN時A點的主應變云圖結果，圖中顏色越深表明相應的應變值越大。通過應變云圖，可以直觀、清晰地判斷出相機視場內試件表面的應變分布及最大應變所在位置。

(a) ε1

(b) ε2

提取各荷載下試件表面A點的第一主應變ε1和第二主應變ε2，得到相應的3次測量結果如表4所示。

表4　三維DIC方法測得的A點主應變

根據試件彈性模量、泊松比，利用有限元分析軟件ANSYS對其進行數值分析，圖5是荷載為2.0 kN時試件的主應變結果。對比圖4和圖5的應變云圖可以發現，根據三維DIC和有限元分析得出的第一、第二主應變的分布非常相似。

(a) ε1

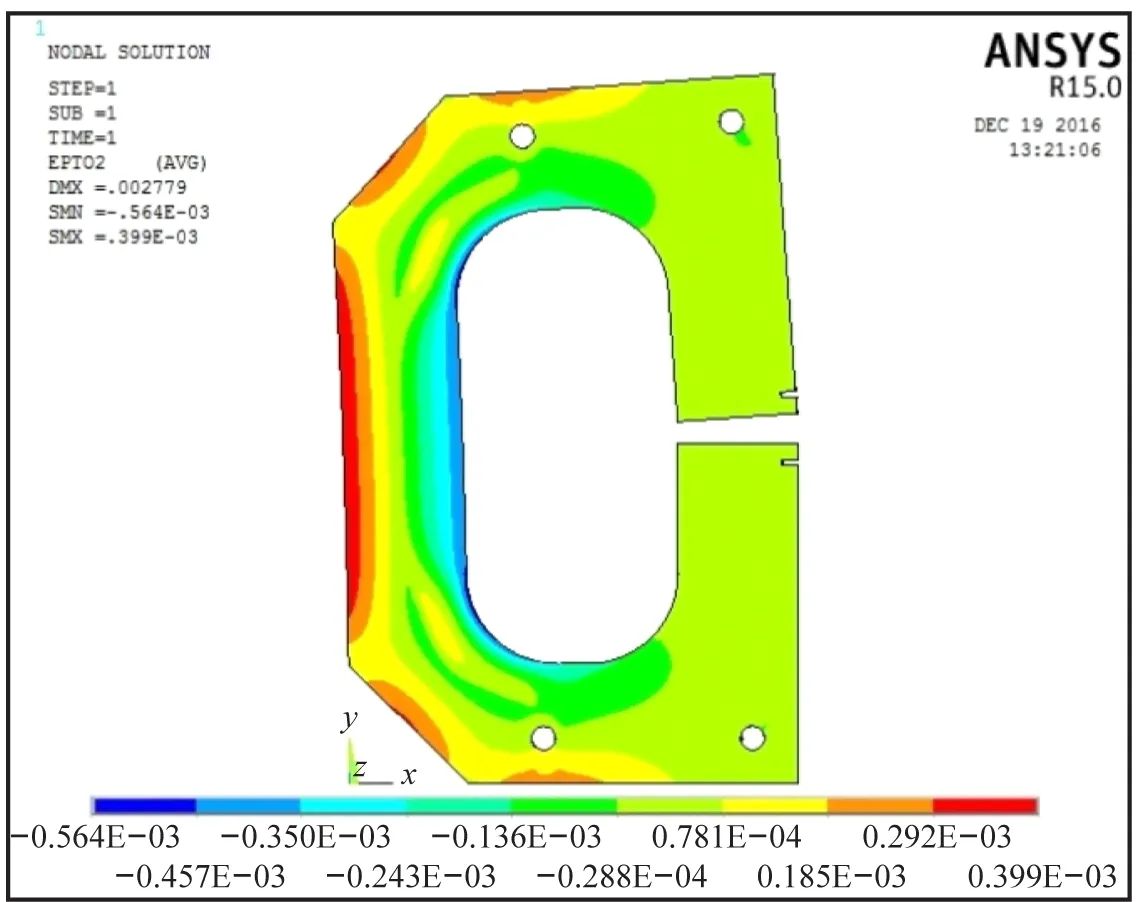
(b) ε2

提取出有限元數值計算結果中A點的主應變結果，并與前面電測法和三維DIC方法的結果進行對比，結果如圖6所示(取3次結果的均值)。圖4、5表明A點附近的應力(應變)變化比較劇烈，在提取A點有限元結果時，會由于定位不夠準確而造成一定的誤差，因此圖6中有限元結果的線性度并不夠理想。對于小應變(ε=0.001×10-6以下)的測試，電測法測得的結果線性比較好，測得的應變值最接近有限元法，三維DIC不如電測法精確。

三維DIC法與電測法相比，第一主應變誤差均值和方差分別為-58.73 ×10-6和53.27 ×10-6，第二主應變誤差均值和方差分別為-5.85 ×10-6和2.85 ×10-6。三維DIC的全場應變測量精度約為100 ×10-6，若由三維DIC法測得A點的3個應變分量分別為εx、εy和γxy，由主應力計算式(2)和不準確度計算式[16]，可算得三維DIC法對A點主應力的測量精度約為90 ×10-6，在用于較大應變測量時，完全可以滿足工程測量的要求。雖然三維DIC法應變精度不如電測法，但它有如下獨特優勢：① 很適合大應變的測量(可達2 000%)；② 能進行非接觸、全場變形測量，得到直觀的測量結果。此外，對于復雜構件應力梯度較大點的應力狀態測量，三維DIC也能得到較為準確的結果，而電測法很難預判其準確位置并進行貼片，故很難給出準確的測量結果。

(a) ε1

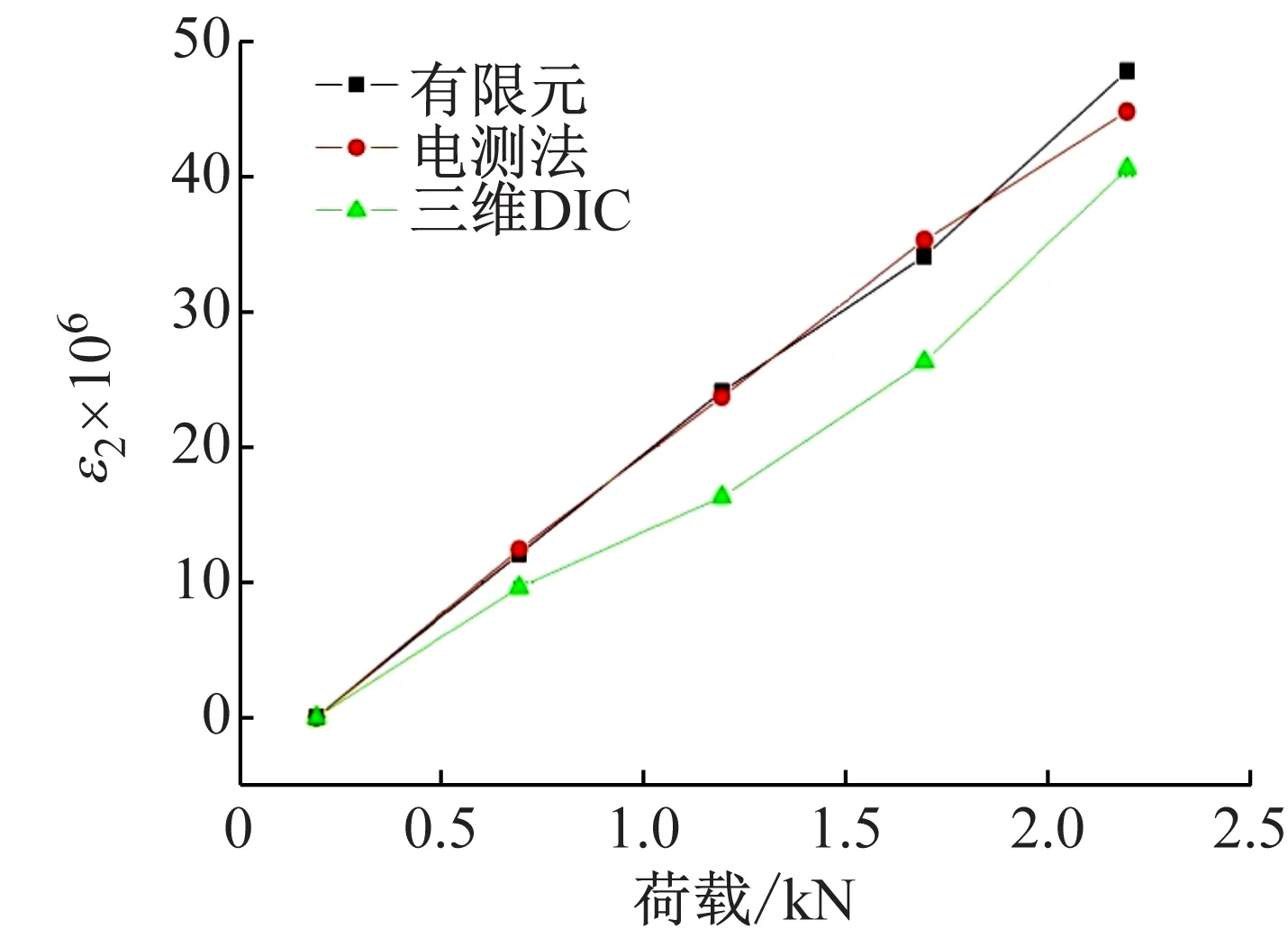
(b) ε2

4　結　論

基于一個偏心拉伸構件的拉伸試驗，比較了三維DIC方法與電測法及有限元方法在用于應力梯度較大點的應變狀態測量時的結果，得到如下結論：

(1) 電測法與有限元分析的主應變結果很接近，而三維DIC則與電測法得到的第一主應變有-58.73×10-6的誤差，第二主應變則相差無幾；不確定度分析表明：三維DIC主應變測量時約有90×10-6的誤差。

(2) 三維DIC具有非接觸、全場、大應變測量等優于電測法的優點，測量時不需事先人為分析危險點位置，其應變結果可直觀反映出危險點所在位置，因此三維DIC非常適用于復雜構件應力梯度較大點的應變(應力)狀態測量。

參考文獻(References)：

[1]劉斐. 電阻應變測試技術在土木工程中的應用[J]. 公路與汽運, 2005(3):93-94.

[2]柴繼新, 王恩鋒, 范小燕,等. 幾種常見的電阻應變式旋轉扭矩傳感器[J]. 計測技術, 2010, 30(2):34-36.

[3]郭懷天, 李寶華, 趙玉俠,等. 基于電阻應變式傳感器的電子天平的研制[J]. 微計算機信息, 2007, 23(6S):140-142.

[4]岳澄, 王燕群, 邵立國,等. 高溫封隔器膠筒與套管接觸壓力的實驗研究[J]. 實驗力學, 1999(3):390-394.

[5]李巧真, 李剛, 韓欽澤. 電阻應變片的實驗與應用[J]. 實驗室研究與探索, 2011, 30(4):134-137.

[6]高曉丁, 胥光申, 王錦. 電阻應變片貼裝方位偏差對測量結果的影響[J]. 西安石油大學學報(自然科學版), 2001, 16(6):41-43.

[7]黃進, 陶睿, 江真丞,等. 選擇不同應變花對主應力測試結果的影響[J]. 實驗室研究與探索, 2016, 35(7):32-36.

[8]潘兵, 謝惠民, 李艷杰. 用于物體表面形貌和變形測量的三維數字圖像相關方法[J]. 實驗力學, 2007, 22(6): 556-567.

[9]項大林, 榮吉利, 何軒,等. 基于三維數字圖像相關方法的水下沖擊載荷作用下鋁板動力學響應研究[J]. 兵工學報, 2014, 35(8):1210-1217.

[10]郝文峰, 原亞南, 姚學鋒,等. 基于數字圖像相關方法的含雙裂紋復合材料薄板應力強度因子測量[J]. 玻璃鋼/復合材料, 2015(4):22-26.

[11]Zhu F, Bai P, Zhang J,etal. Measurement of true stress-strain curves and evolution of plastic zone of low carbon steel under uniaxial tension using digital image correlation [J]. Optics and Lasers in Engineering, 2014, 65: 81-88.

[12]Lei D, Huang Z, Bai P,etal. Experimental research on impact damage of Xiaowan arch dam model by digital image correlation [J]. Construction and Building Materials, 2017, 147: 168-173.

[13]Luo P, Chao Y, Sutton M,etal. Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision [J]. Experimental Mechanics, 1993, 33(2): 123-132.

[14]唐正宗, 梁晉, 肖振中,等. 用于三維變形測量的數字圖像相關系統[J]. 光學精密工程, 2010, 18(10):2244-2253.

[15]潘兵, 謝惠民. 數字圖像相關中基于位移場局部最小二乘擬合的全場應變測量[J]. 光學學報, 2007, 27(11): 1980-1986.

[16]曹宏燕. 分析測試中的測量不確定度及評定 第二部分測量不確定度評定的基本方法[J]. 冶金分析, 2005, 25(2):84-87.