MEMS手勢軌跡繪制系統設計

邵　帥，　李明哲，　許　睿，　宋華軍

(1. 中國石油大學(華東) 信息與控制工程學院，山東 青島 266580； 2. 天津大學 電氣自動化與信息工程學院，天津 300072)

0　引　言

傳統的人機交互方式包括觸摸屏、語音識別等存在一定的局限性，比如觸摸屏必須限定在設備屏幕上使用；語音識別技術在嘈雜環境中或使用方言時效果不盡人意。而基于MEMS慣性傳感器的無接觸軌跡重構手勢識別方式，彌補了傳統的人機交互方式的不足，具有直觀、自然、易于學習等優勢，可應用在無接觸手寫電子筆[1]，體感游戲，空中鼠標，遙控器空中寫數字換臺等處。

捷聯慣性導航技術具有很強的抗干擾能力，隨著近20年微電子機械系統(Micro Electro Mechanical System，MEMS)的較快發展[2]，捷聯慣導技術得到進一步完善。MEMS慣性傳感器包括陀螺儀和加速度計，具有成本低、體積小、質量輕、功耗低、靈敏度高、易于集成，以及適應性強等特點，對于智能手機等移動設備而言，基于MEMS慣性傳感器的手勢識別方法比基于視頻的識別方法更為適用。

已有系統多采用獨立的陀螺儀、加速度計等多個傳感器組合進行姿態解算，存在多個芯片占用空間大、姿態數據存在軸間誤差、數據融合精度欠佳等不足。本文設計了基于MEMS的手勢軌跡繪制系統，選取集成加速度計、陀螺儀和磁力計于一體的MPU9250為核心芯片，用來采集九軸原始數據，包括三軸加速度、三軸角速度和三軸磁場。然后在STM32單片機上進行姿態解算，最后通過藍牙將原始數據和姿態數據傳給上位機，在上位機完成軌跡重構。

1　系統硬件部分設計

1.1　硬件結構設計

硬件電路核心為STM32F4單片機與MPU9250芯片。電路采用USB接口供電，通過3.3 V穩壓芯片，確保電源輸出穩定電壓，保證芯片正常工作。通過A/D轉換計算電池電量，在電池電量不足時控制LED燈報警。MPU9250芯片作為數據采集芯片，無需A/D轉換器就可直接將數據通過I2C傳送到單片機中進行處理，減小系統能耗。同時外接藍牙模塊，與上位機進行交互，結構圖如圖1所示。

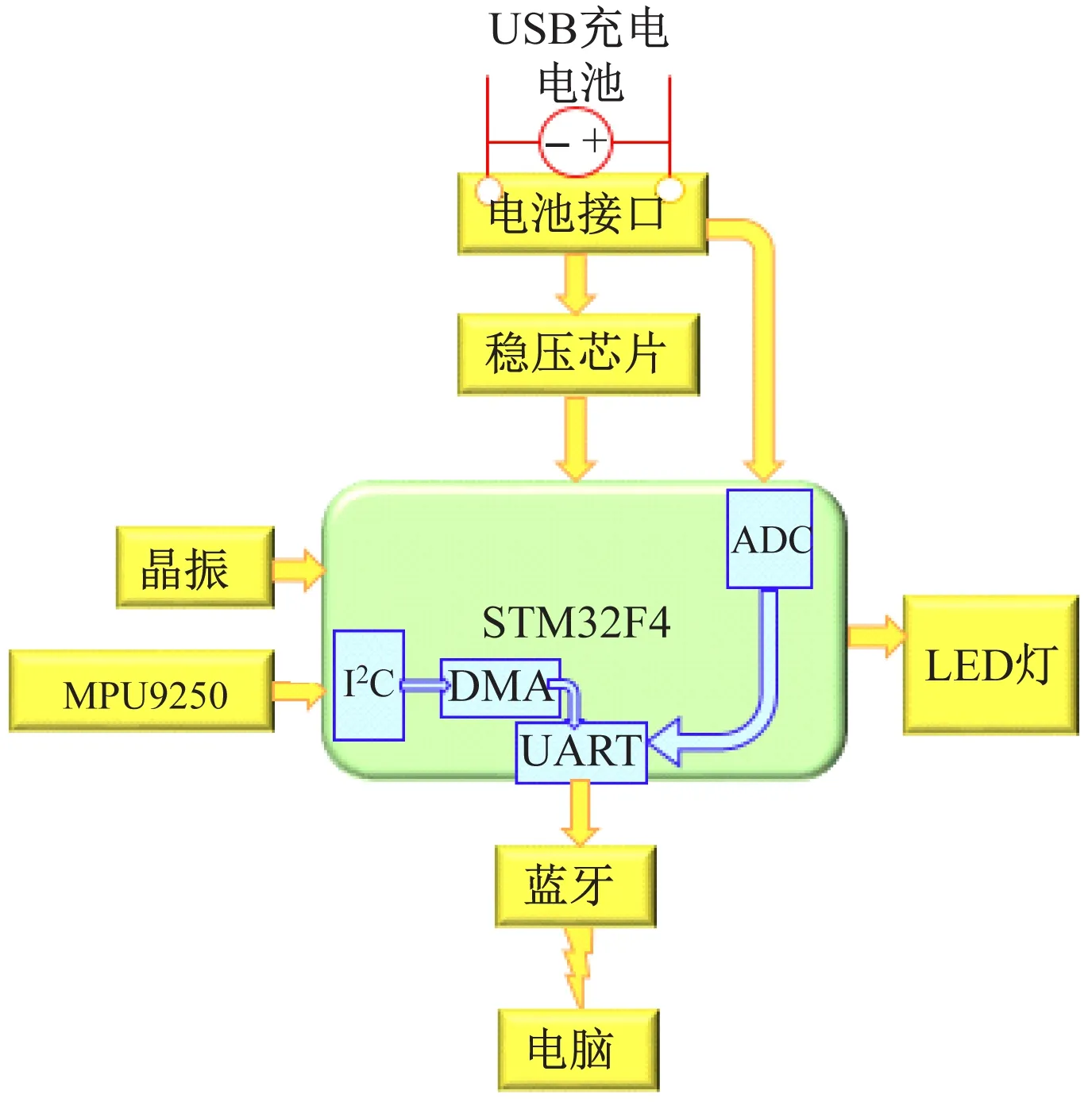
圖1　硬件部分結構圖

1.2　硬件系統的軟件流程

軟件流程圖如圖2所示。單片機上電后，首先對各個模塊進行調試，當調試完成后，對系統初始化， MPU9250采集原始數據并發送到單片機中，單片機接收數據后，運行姿態解算算法，當檢測每完成一個手勢動作后，都觸發一個外部中斷，讓姿態解算算法重新運行。在解算同時，將原始九軸數據和解算好的四元數通過藍牙模塊實時傳給上位機。

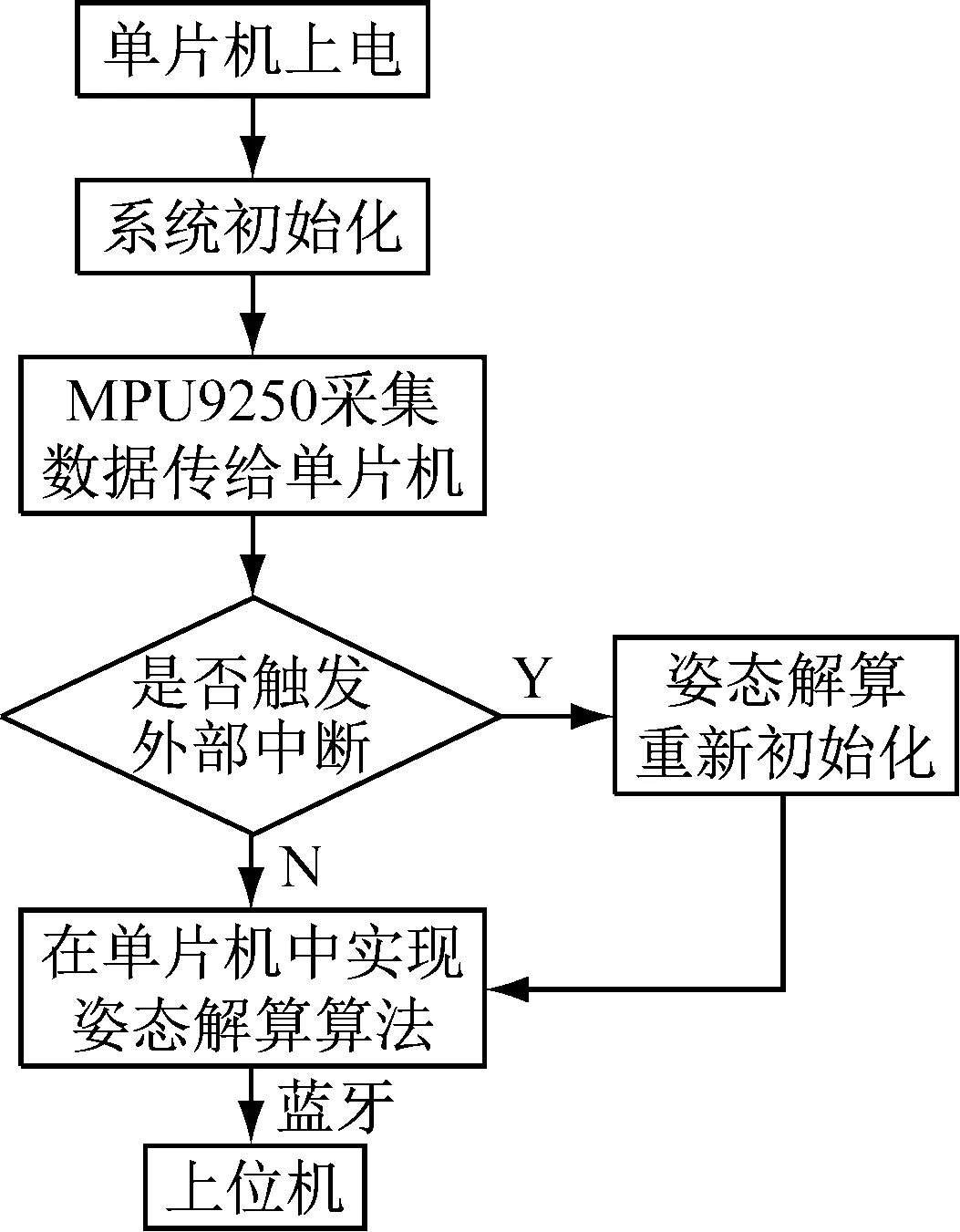
圖2軟件流程圖

2　系統實現算法

2.1　算法流程

整個系統的算法流程圖如圖3所示，在一個完整手勢流程內，MPU9250采集九軸數據后，先用其中的三軸加速度和三軸磁場數據計算初始歐拉角，其中MPU9250測的三軸加速度數據被稱為載體坐標系[3]加速度。然后將初始歐拉角轉換為初始四元數，再與三軸角速度結合，根據陀螺積分的方法更新下一時刻的四元數，直到這個手勢流程結束。根據每個時刻的四元數與載體坐標系加速度計算出該時刻地理坐標系[3]加速度，再對地理坐標系加速度進行雙重積分得到每個時間段的位移，最終形成相應軌跡。

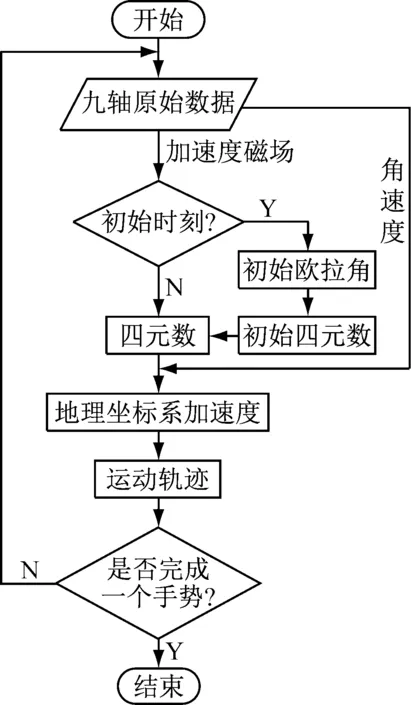
圖3算法流程圖

2.2　初始姿態解算原理

載體坐標系(b系)中，MPU9250采集的加速度值可表示為acc=[axb,ayb,azb]T，磁場強度可表示為mag=[mxb,myb,mzb]T。在平穩狀態下，地理坐標系(n系)中，重力場G=[0,0，-g]T,磁場強度M=[0,my,mz]T,可在載體坐標系中由下式表示為：

(1)

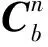
(2)

ψ，θ，Φ分別代表繞z、y、x軸轉動角度。

將式(2)代入式(1)可得：

(3)

式中：D為磁偏角，是一個固定值，可由查表或大量實驗得到。此種用加速度和磁力結合的解算方法，只適用于物體靜止或低動態的情況，所以在確定初始姿態時應該讓物體保持靜止10 s時間，然后采集該10 s數據的平均值作為測量值。得到初始的歐拉角以后，通過下式將初始的歐拉角轉換成初始的四元數：

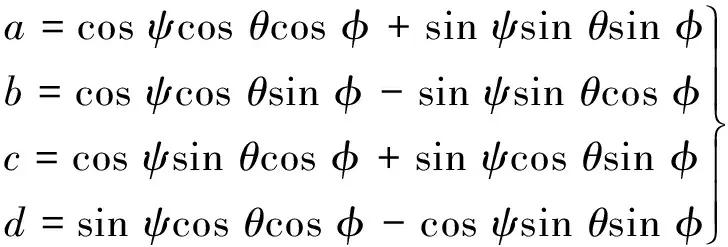
(4)

需要注意的是，繞坐標軸不同的旋轉順序會得到不同的四元數公式，式(4)是按照繞“zyx”的順序得到的。

2.3　姿態的更新

在得到初始姿態后，可根據慣導原理，對姿態不斷進行更新，更新方程為：

(5)

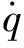
(6)

式中：ωx,ωy,ωz分別代表t-1時刻的三軸角速度；Δt是采樣間隔。根據式(6)可得不斷更新的四元數，在初始四元數較準確的前提下，此時在高動態時也可有較高的準確率。

2.4　軌跡重構

在求軌跡時，應先通過下式，將載體坐標系加速度轉換成地理坐標系加速度。

(7)

式中：axb，ayb，azb表示載體坐標系下的三軸加速度；axn，ayn，azn表示地理坐標系下的加速度。

該系統采集的加速度都是以“g”為單位，所以在雙重積分求得軌跡之前，先通過下式，將加速度的單位轉換成標準單位(m/s2)。其中z軸的加速度，要去掉重力的影響。

axN=axng，ayN=ayng，azN=(azn-1)g

(8)

式中：axN，ayN，azN表示地理坐標系下，不受重力影響具有標準單位的三軸加速度。

根據式(9)求三軸加速度的向量模，然后設定一個閾值，只有在當向量模大于該閾值時，系統才會被判斷為在進行軌跡重構，

(9)

通過下式分別對三軸的加速度進行雙重積分，可求得載體在三軸上的位移，分別由Sx，Sy，Sz表示：

Sx=?axNdt，Sy=?ayNdt，Sz=?azNdt

(10)

3　實驗結果分析

設計的手勢軌跡繪制系統電路板如圖4所示，板大小為35 mm×17 mm。

3.1　“對號”實驗

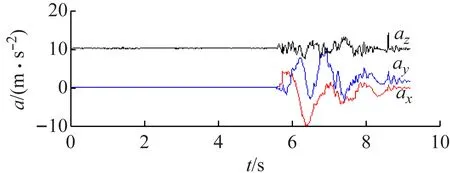
手拿傳感器畫“對號”，相應加速度如圖5所示。

圖4　電路板

(a) 載體坐標系

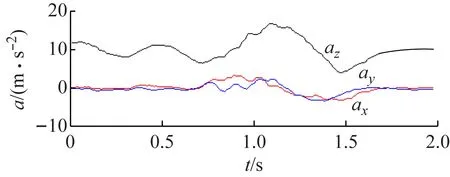
(b) 地理坐標系

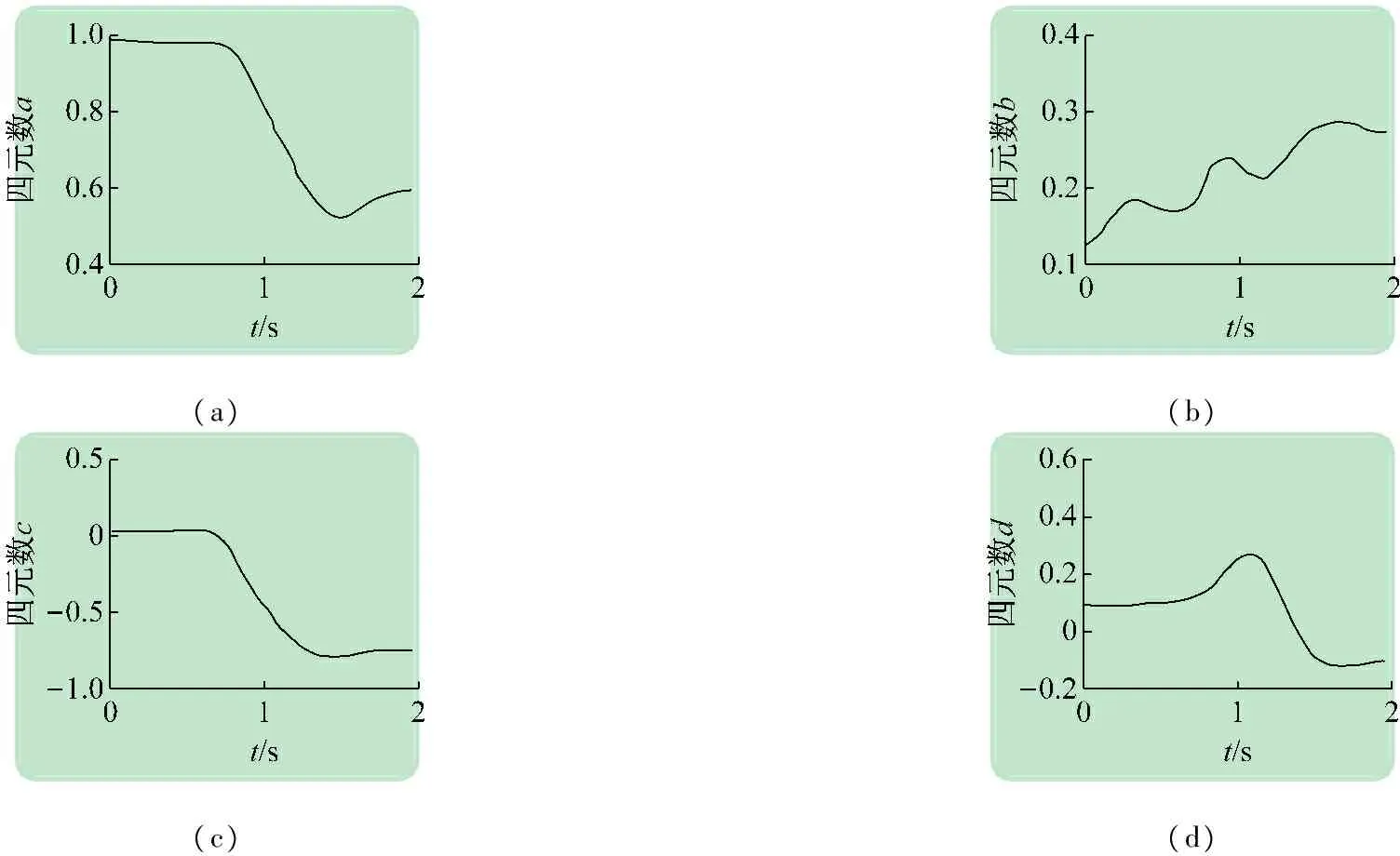
解算的四元數如圖6所示。“對號”圖如圖7所示。

(a)(b)(c)(d)

圖6畫對號解算的四元數

由圖5～7可看出，該系統在做手勢畫“對號”時，清晰地展現了圖形的形狀和尺寸大小。

3.2　“8”實驗

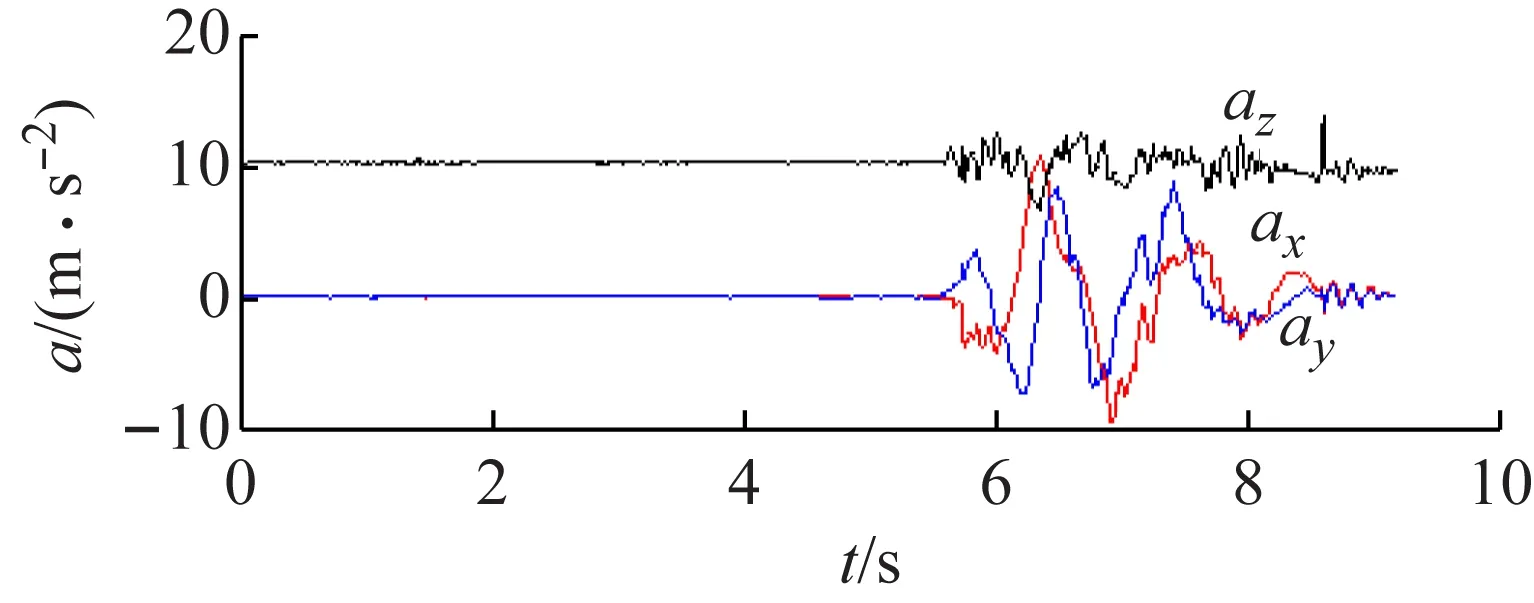
手拿傳感器在空間寫“8”，相應加速度見圖8，相應四元數見圖9，數字“8”如圖10所示。

由圖8～10可見，在空間中畫閉環圖形時，只要調整觀看圖形時的角度，也可得到圖形清晰的形狀和尺寸大小。

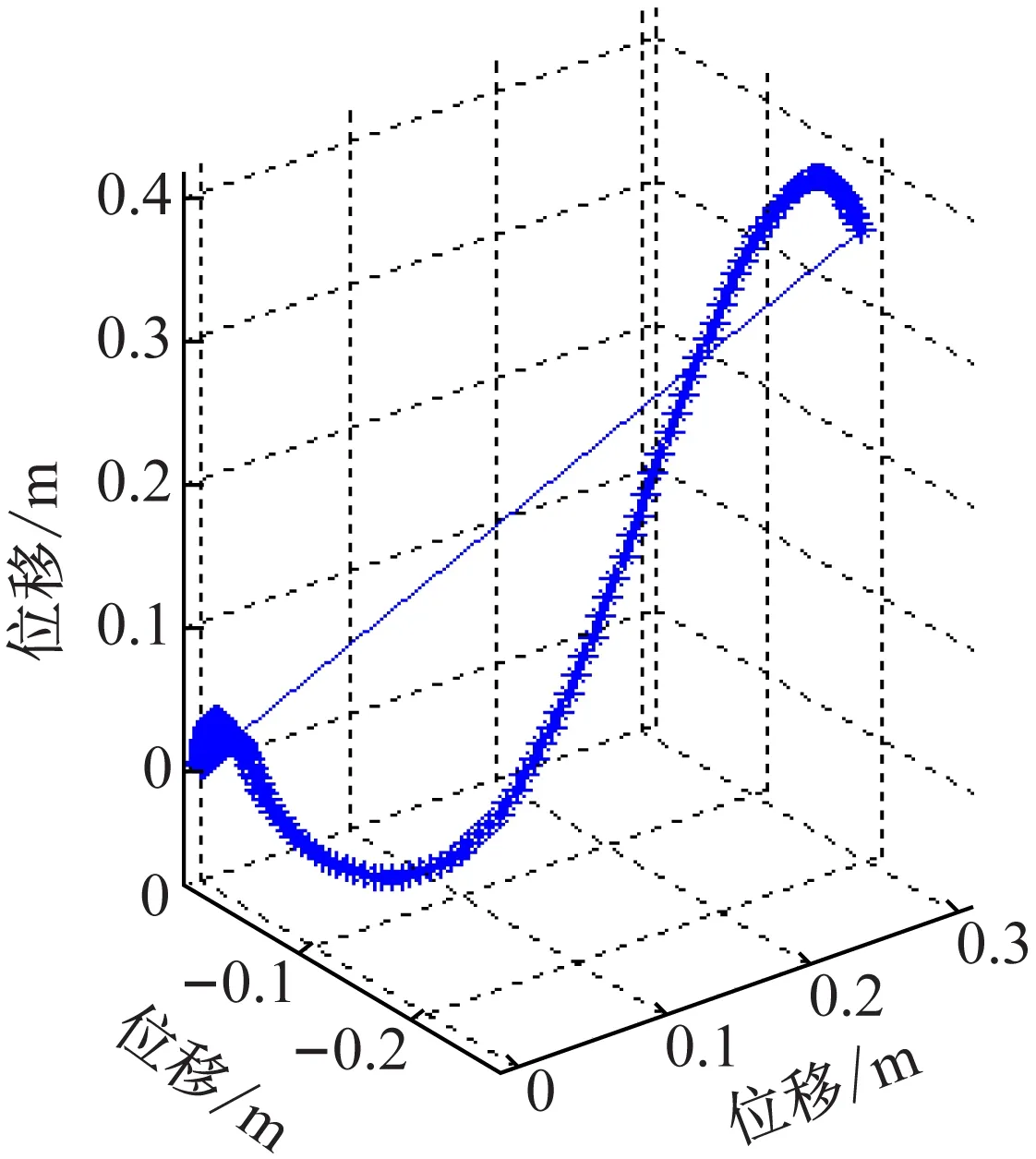
圖7　對號圖

(a) 載體坐標系

(b) 地理坐標系

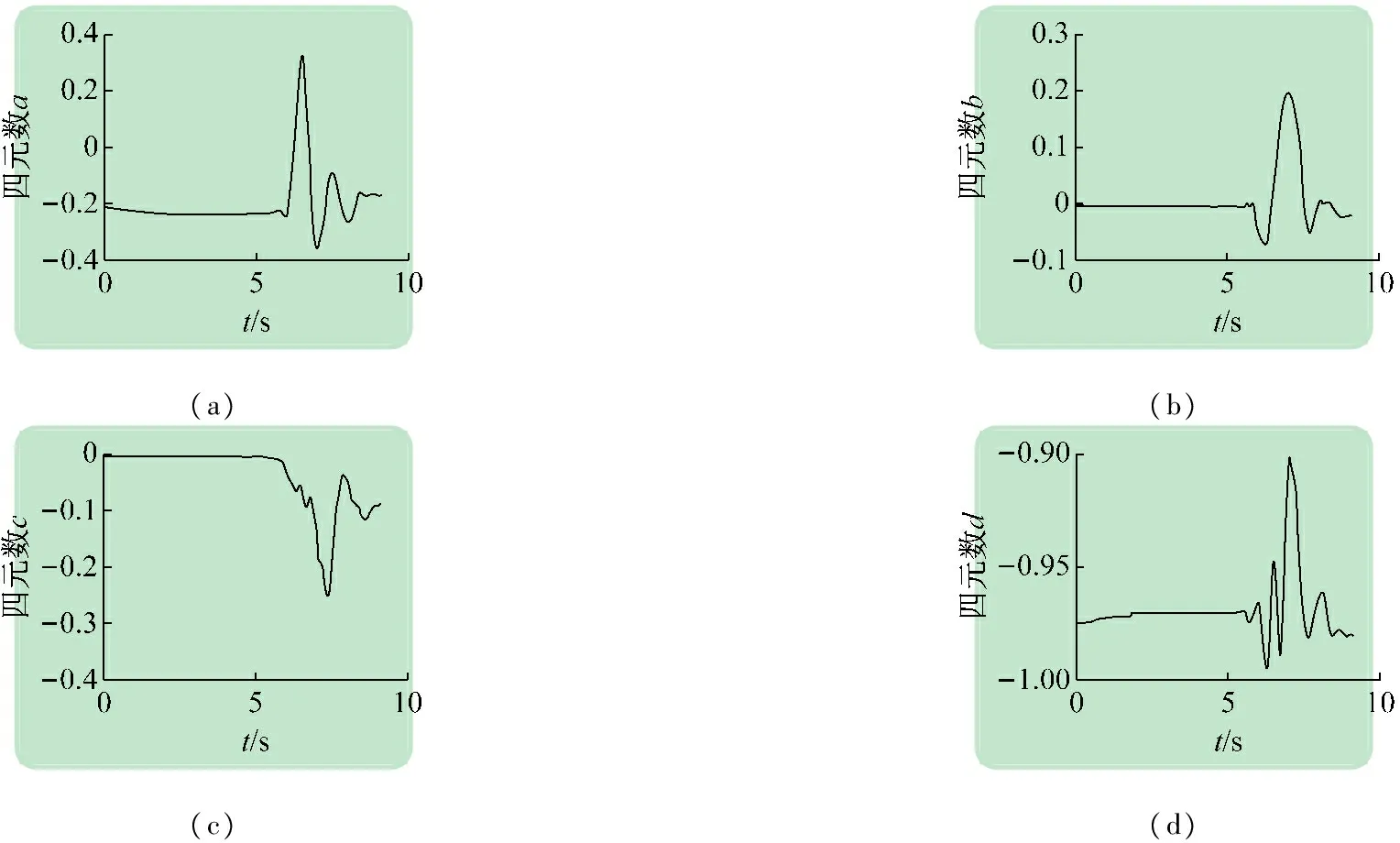
(a)(b)(c)(d)

圖9畫數字“8”解算的四元數

這兩組實驗分別完成了此系統在空間中開環圖形和閉環圖形的繪制，都可以清晰、直觀地反映該系統的工作效果，能夠完成軌跡的正確繪制。

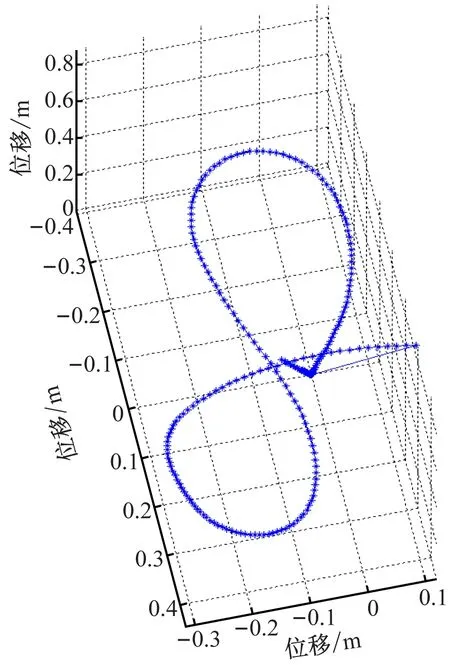
圖10　數字“8”三維圖

4　結　語

本文設計的系統完成了系統硬件的制作，并對原始數據進行處理，最后在上位機生成軌跡。實驗結果充分證明了解算算法和軌跡重構的可行性。

該系統因為采用陀螺積分的方法更新四元數，所以在長時間應用中會產生積分漂移從而造成生成的四元數誤差，本文采用設置中斷的方式來減小積分時間從而減小誤差，但根據加速度膜的大小來判斷手勢軌跡完成與否有時會產生誤判，并且每次中斷以后重新計算初始四元數時，不能保證每次都在平穩環境下計算，也會產生計算誤差。在后續研究中，將考慮廣義卡爾曼濾波與慣性導航知識相結合的方法來進行解算研究。

參考文獻(References)：

[1]Leong H W，Li W J. Handwriting tracking based on coupled IMU/electromagnetic resonance motion detection[C]//International Conference on Robotics and Biomimetics. Sanya,2007：377-381.

[2]王淑華.MEMS傳感器現狀及應用[J]. 微納電子技術,2011,48(8):516-522.

[3]張天光，王秀萍，王麗霞.捷聯慣性導航技術[M].2版.北京：國防工業出版社，2007.12.

[4]王粉花, 張萬書. 基于手勢識別技術的3D虛擬交互系統[J]. 實驗室研究與探索, 2014, 33(6):94-98.

[5]陳孟元, 謝義建, 陳躍東,等. 基于四元數改進型互補濾波的MEMS姿態解算[J]. 電子測量與儀器學報, 2015, 29(9):1391-1397.

[6]夏齡, 周德榮, 陳鵬,等. 基于手勢識別的S195型柴油機虛擬裝配[J]. 實驗室研究與探索, 2015, 34(9):84-86.

[7]常敏, 崔永進, 何蓓薇,等. 四軸飛行器姿態控制系統設計[J]. 通信電源技術, 2015(5):144-147.

[8]謝寧, 畢俊熹, 婁小平,等. 融合多傳感信息的仿人機器人姿態解算[J]. 電子科技, 2015, 28(1):150-154.

[9]仇立杰. 基于MEMS傳感器的手勢識別算法研究[D]. 北京：北京化工大學, 2016.

[10]Srihari S N, Cha S H, Arora H,etal. Individuality of handwriting: A validation study[C]// International Conference on Document Analysis and Recognition. IEEE Computer Society, 2001:106.

[11]季怡, 楊帆, 龔聲蓉,等. 基于Adaboost實現的實時手勢識別[J]. 實驗室研究與探索, 2014, 33(8):123-126.

[12]周樹道, 金永奇, 衛克晶,等. 采用卡爾曼濾波算法的MEMS器件姿態測量[J]. 實驗室研究與探索, 2015, 34(2):38-42.

[13]《實驗室研究與探索》編輯部. 航天器姿態控制新型慣性執行機構技術[J]. 實驗室研究與探索, 2009, 28(10):I0001-I0002.

[14]張榮輝, 賈宏光, 陳濤,等. 基于四元數法的捷聯式慣性導航系統的姿態解算[J]. 光學精密工程, 2008, 16(10):1963-1970.

[15]Lagardere X, Gonzalez A. Gesture recognition: US, US7372993[P]. 2008.

[16]Mitra S, Acharya T. Gesture recognition: A survey[J]. IEEE Transactions on Systems Man & Cybernetics Part C, 2007, 37(3):311-324.