旋轉式SINS的自標校技術研究

王　坤，殷廷巍，奔粵陽

(1.哈爾濱工程大學 自動化學院，哈爾濱 150001;2.大連426廠，大連 116005)

0　引言

捷聯慣導系統是一種自主式導航定位系統，短期內精度高，穩定性好[1]，但其定位誤差會隨著時間發散[2-4]，慣性器件誤差是影響其發散的關鍵因素，而且該誤差量在實際使用中會產生微小變化。為提高慣導系統的導航精度，需要對慣性器件誤差進行現場標校[5]。雙軸旋轉式慣導系統就是通過轉位機構在不同的轉位方案下，充分激勵出慣性器件誤差，并通過Kalman濾波進行估計補償[6]。

目前，系統級標定的理論研究已經趨于成熟，文獻[2]提出了10位置連續旋轉方案，并利用Kalman濾波進行誤差估計，但其穩定時間較長。文獻[3]給出了平臺多位置快速自標定方法，但沒有分析轉軸精度對估計精度的影響。本文建立了IMU誤差模型，推導了雙軸旋轉捷聯慣導系統誤差公式，建立了Kalman狀態方程，并提出一種8位置雙軸標定方案，對慣性器件誤差進行仿真分析，由實驗結果充分證明其有效性和可行性，對于高精度慣導系統，具有一定的工程意義。

1　旋轉調制慣導原理與雙軸旋轉式SINS的自標校方案設計

1.1　系統常用坐標系

1)地理坐標系(t系)——oxtytzt

地理坐標系是原點o位于地球表面任意一點，oxt指向水平東向，oyt軸指向水平北向，ozt沿垂線方向指向天，通常稱為東北天坐標系[7]。

2)導航坐標系(n系)——oxnynzn

根據慣導系統的工作需求提出了導航坐標系的概念。將地理坐標系作為導航坐標系，這種導航坐標系稱為當地水平固定指北方位坐標系。

3)載體坐標系(b系)——oxbybzb

載體坐標系是固連在載體上的坐標系。載體坐標系的坐標原點o位于載體的重心處，縱軸oyb在甲板平面指向艦首，橫軸oxb指向其右舷，ozb垂直于oxbyb構成右手坐標系[7]。

4)慣性測量單元坐標系(s系)——oxsyszs

慣性測量單元坐標系又稱IMU坐標系，為旋轉調制系統需求設定的坐標系。坐標系的原點位于慣性測量組件的重心，三軸指向為慣性器件敏感軸方向[8-10]。

旋轉式SINS捷聯慣導系統主要是靠不同轉位方案激勵出慣導器件的誤差，再通過Kalman濾波對其誤差狀態變量進行估計，對其誤差結果進行補償，從而提高捷聯慣導系統的輸出精度。另外，基于實際情況考慮，為提高系統的可靠性，降低對轉位機構的要求，通過最少的轉動次數和較短的轉動達到最優的誤差估計效果，本文基于該設計原則，設計了3組轉位方案。

1.2　雙軸4位置旋轉方案的設計

雙軸4位置旋轉方案的具體設計如下：

由初始位置1繞ys軸按正向旋轉90°后到位置2；由位置2繞xs軸按正向旋轉180°后到位置3；由位置3繞ys軸按反向旋轉90°后到位置4；由位置4繞xs軸按反向旋轉180°后到初始位置1，轉位方案如圖1所示。

1.3　雙軸6位置旋轉方案的設計

雙軸6位置旋轉方案的具體設計如下：

由初始位置1繞ys軸按正向旋轉90°后到位置2；由位置2繞ys軸按正向旋轉90°后到位置3；由位置3繞xs軸按正向旋轉180°到位置4；由位置4繞ys軸按反向旋轉90°到位置5；由位置5繞ys軸按反向旋轉90°到位置6；由位置6繞xs軸按反向旋轉180°到初始位置1，旋轉方案如圖2所示。

1.4　雙軸8位置旋轉方案的設計

雙軸8位置旋轉方案的具體設計如下：

由位置1繞xs軸按正向旋轉180°后到位置2；由位置2繞xs軸按正向旋轉90°后到位置3；由位置3繞xs軸按反向旋轉180°后到位置4；由位置4繞xs軸按反向旋轉90°后到位置1；由位置1繞ys軸按正向旋轉90°后到位置5；由位置5繞xs軸按正向旋轉180°后到位置6；由位置6繞xs軸按正向旋轉90°后到位置7；由位置7繞xs軸按反向旋轉180°后到位置8；由位置8繞xs軸按反向旋轉90°后到位置5；由位置5繞ys軸按反向旋轉90°后到位置1，旋轉方案如圖3所示。

2　SINS的數學模型與Kalman濾波方法

捷聯慣導的誤差方程是研究捷聯慣導系統的基礎，本文以東北天坐標系為參考系[11]，建立了其捷聯慣導系統的速度、位置和姿態誤差方程[12]，以便對慣性器件進行誤差補償，并建立Kalman濾波方程，通過轉位方案的激勵[13-14]，對器件誤差進行估計補償，達到最優效果。

2.1　速度誤差方程

速度誤差定義為

δvn=vc-vn

(1)

式中，vc為計算坐標系下計算的速度。

式(1)兩邊同時對求導

其中：

(2)

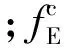
由于陀螺漂移和計算誤差的存在，計算坐標系c系和導航坐標系n系之間存在著小角度的誤差量φE、φN、φU，稱為姿態誤差角。且φE、φN、φU為小角度，有sinφ≈φ，cosφ≈1(其中φ=φE,φN,φU)成立，計算坐標系c系和導航坐標系n系之間轉換關系可化簡為

(3)

得

(4)

定義位置誤差項為：

(5)

其中，L、λ分別為實際位置的緯度、經度。

(6)

利用式(4)、式(5)和式(6)可得SINS速度誤差方程[5]：

(7)

2.2　位置誤差方程

位置誤差即經緯度誤差和高度誤差，是由于載體在東向、北向和天向的速度存在誤差引起的。經緯度的變化率和載體線運動的關系為：

(8)

(9)

將式(5)求導得：

(10)

將式(2)、式(6)、式(8)和式(9)代入式(10)中，可得SINS位置誤差方程：

(11)

2.3　姿態誤差方程

捷聯慣導系統的姿態誤差角是通過方向余弦法所得到的計算地理坐標系與真實地理坐標系間的角度關系[15]。

平臺運動基本方程為：

(12)

其中，εx、εy、εz為陀螺漂移引起的誤差在導航坐標系的等效值；ωx、ωy、ωz為地理坐標系旋轉角速度，且有：

(13)

將式(13)代入式(12)可得姿態誤差方程：

(14)

2.4　Kalman濾波模型

建立旋轉式光纖陀螺捷聯慣導系統的Kalman濾波方程，其中狀態方程為

(15)

其中，X(t)為t時刻系統的狀態向量，F(t)為系統的狀態轉移矩陣，G(t)為系統的噪聲驅動陣；W(t)為系統噪聲向量。

本文的系統的狀態向量為

(16)

系統的噪聲向量為

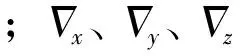
以速度誤差作為量測量，則系統的量測方程為

Z(t)=H(t)X(t)+V(t)

(17)

其中，Z(t)為t時刻系統的量測向量；V(t)為系統的量測噪聲。系統的量測矩陣為

H(t)=[02×2I2×202×12]

3　仿真結果及分析

利用VC程序編寫的對慣導系統進行建模，并利用Kalman濾波方法對慣性器件誤差及失準角進行慣性器件誤差狀態變量估計，采用輸出補償的方式對其實驗結果進行分析。在相同的初始條件下對三種方案進行仿真，仿真參數如表1所示。

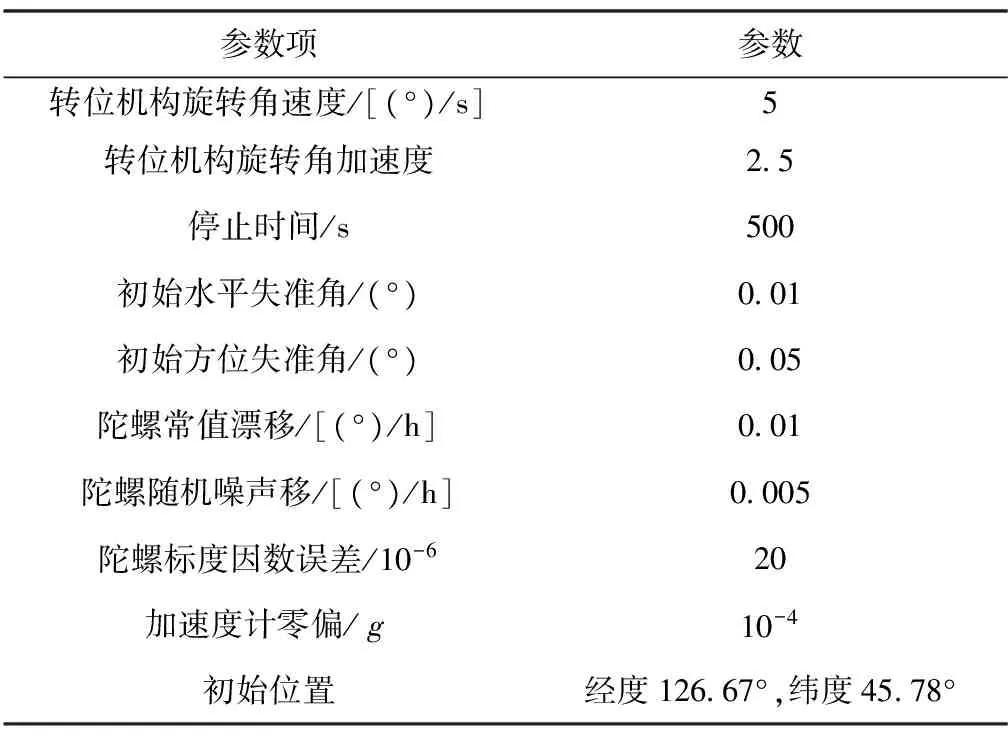
表1　仿真參數設置

3.1　失準角誤差估計與分析

圖4所示為失準角誤差的估計結果，由圖4可知，三種旋轉方案的失準角估計效果都能穩定，并收斂于零度左右，收斂時間最好的是4位置轉位方案，40min基本穩定收斂于設定真值附近。

3.2　陀螺常值漂移估計與分析

圖5所示為陀螺常值漂移的估計效果，由圖5可知，本文提出的三種方案的仿真對其陀螺常值漂移誤差達到很好的估計效果。對于x軸上的常值漂移效果來說，4位置的轉位方案最先達到穩定，大約20min左右，8位置的收斂速度較差，大約3h穩定；就y軸的估計效果來說，8位置轉位方案比4位置和6位置的轉位方案的收斂速度更快更穩定，且穩定與真值附近；z軸的常值漂移誤差估計效果與y軸相似。

3.3　加速度計零偏估計與分析

圖6所示為加速度計零偏的估計效果，由圖6可知，三種旋轉方案都能較好地激勵出加速度計的零偏，估計效果穩定于設定真值。就x軸加速度計零偏來說，4位置和6位置轉位方案在30min內收斂于設定真值，8位置的收斂速度較慢；y軸的估計效果中，4位置和6位置轉位方案的收斂速度很慢，且穩定值與設定真值有偏差，8位置轉位方案在1h左右能穩定在真值附近；z軸的效果和y軸加速度計估計效果類似。

3.4　標度因數誤差估計與分析

對標度因數誤差的估計效果如圖7所示，從圖7可知，對轉位方案對標度因數的誤差激勵作用不理想，8位置的轉位方案能有效激勵出標度因數誤差，但穩定時間較長；4位置和6位置的轉位方案能夠較好地估計出x軸的陀螺的標度因數誤差，在5h左右達到仿真設定真值，但無法估計出y軸和z軸的陀螺的標度因數誤差。

根據上面對失準角誤差、陀螺漂移、加速度計零偏和陀螺儀標度因數誤差的估計結果，綜合仿真曲線分析可得：8位置的轉位方案能夠有效激勵出其所有的誤差量，性能優于4位置和6位置轉位方案，因此，本文中提出的8位置轉位方案是一種有效的優秀的誤差標校方案。

4　結論

文中共提出了三種不同的轉位方案，即4位置轉位方案、6位置轉位方案和8位置轉位方案，并進行了VC程序的建模和實驗仿真。由實驗結果分析可知，8位置轉位方案是一種有效可行的雙軸旋轉捷聯慣導系統的自標校方案，能夠有效地激勵出慣性器件的陀螺漂移、加速度計零偏和陀螺標度因數誤差，并進行輸出補償，有效地提高了慣導系統精度。由圖5～圖7可知：陀螺常值漂移和加速度計零位誤差估計效果與設定真值僅差4%，陀螺標度因數誤差的估計效果與設定真值差5%。此次雙軸旋轉仿真實驗是在靜基座條件下進行的，忽略了實際機體運動對器件誤差的影響，后續的工作重點是引入機體運動，結合實際情況進行仿真和船體實驗。

[1]于旭東 . 二頻機抖激光陀螺單軸旋轉慣性導航系統若干關鍵技術研究[D].長沙: 國防科技大學, 2011.

[2]石文峰,王省書,鄭佳興,等. 激光陀螺捷聯慣導系統多位置系統級標定方法[J]. 紅外與激光工程,2016,45(11): 92-99.

[3]肖正林,錢培賢,徐軍輝. 三軸平臺快速自標定與自對準方法探討[J]. 宇航學報,2006,27(2):222-226.

[4]陳哲.捷聯慣導系統原理[M]. 北京: 中國宇航出版社,1986.

[5]System Requirements Document for the MK39 Mod3C for the Republic of Singapore[S]. SR1898389 Rev, 1998.

[6]李兵軍. 基于光纖捷聯式羅經系統的初始對準技術[D]. 哈爾濱: 哈爾濱工程大學, 2008.

[7]黃德鳴,程祿. 慣性導航系統[M]. 北京:國防工業出版社, 1986.

[8]魏鳳娟. 捷聯慣導系統的初始對準研究與設計[D]. 哈爾濱: 哈爾濱工程大學, 2003.

[9]Rogers R M. Applied mathematics in integrated navigation systems(3rdEdition)[J]. Reston American Institute of Aeronautics and Astronautics Inc, 2015:78.

[10]袁保倫. 四頻激光陀螺旋轉慣導系統研究[D].長沙: 國防科技大學, 2007.

[11]Yuan B, Liao D, Han S. Error compensation of an optical gyro INS by multi-axis rotation[J]. Measurement Science and Technology, 2012, 23(2):91-95.

[12]Tucker T, Levinson E. The AN/WSN-7B marine gyrocompass navigator[C]//Proceedings of the National Technical Meeting of the Institute of Navigation, 2000:348-357.

[13]Zhou S, Wu X, Li R. Analysis of error propagation characteristics of dual-axis rotary inertial navigation system[J].Chinese Journal of Sensors and Actuators, 2012(10):18.

[14]陸志東,王曉斌. 系統級雙軸旋轉調制捷聯慣導誤差分析及標校[J]. 中國慣性技術學報,2010, 18(2):135-141.

[15]楊曉霞,黃一. 利用ESO和TD進行的激光捷聯慣組誤差參數外場標定方法[J]. 中國慣性技術學報,2010, 18(1):2-9.