作動器輸出機構剛度優化設計與仿真分析

張新華，劉　源，張兆凱，黃　建

( 北京自動化控制設備研究所,北京 100074)

0　引言

電動作動器作為飛控系統的主要部件，對其動態特性有著較高的要求[1]。在電動作動器的實際使用中，當其舵偏角、最大舵偏角速度、頻帶、線性度和超調量等性能指標比較滿意的情況下，仍會出現一些新的問題，這些問題存在的主要原因之一就是作動器的剛度特性不能滿足要求[2]。剛度太差則極易引發舵面的顫振。當顫振發生時，副翼或舵面有很大的偏轉，舵翼發生振動，振幅很大，頻率很高，極易發生危險[3]。

另外，發散、顫振、氣動伺服彈性不穩定等氣動彈性問題往往要等到導彈飛行試驗才暴露出來，而一旦在飛行中發生這類問題，則將直接導致飛行失利[4]。因此，在導彈方案設計階段就需要對氣動彈性問題進行研究，以避免由于導彈方案設計不當而導致氣動彈性問題的發生[5-11]。

作動器的剛度是導彈氣動伺服彈性問題的重要影響因素之一，若剛度較低則使導彈易發生顫振風險[12]。作動器連桿機構剛度的大小是影響其整體機械剛度的主要因素之一，而連桿機構的主要組成部分為輸出機構，因此，輸出機構剛度直接影響作動器的整體性能[13-15]。本文對作動器輸出機構的剛度做重點研究，旨在優化作動器的整體機械剛度，為工程應用提供理論依據。

1　作動器連桿機構剛度的理論分析

電動作動器的連桿機構如圖1所示，考慮輸出機構與轉接桿的彈性變形時，輸出機構的彈性變形可以看作是軸體空心圓柱的扭轉變形與搖臂變截面懸臂梁變形的組合變形；轉接桿的變形可以看作是簡單的拉壓變形；整個連桿機構的變形則是這三種變形綜合作用的結果，可使用組合變形的疊加原理對其進行分析。下面對連桿機構的機械剛度進行詳細推導。

1.1　作動器輸出機構軸體的扭轉變形

由材料力學可知，在圓軸的兩端作用扭轉力偶時，始末截面間繞軸線的相對轉角可以使用式(1)計算，其中，l為圓軸的有效長度，M為扭轉力偶，G為材料的彈性模量，Ip為圓軸截面的極慣性矩。

(1)

對于空心圓軸，截面的極慣性矩為

(2)

其中，D和d分別為空心圓截面的外徑和內徑，α=d/D。

則對于等直圓軸的相對轉角即為

(3)

1.2　作動器輸出機構搖臂的變截面懸臂梁變形

搖臂的數學模型可以簡化成圖2所示。由材料力學可知，撓曲線的近似微分方程為

(4)

將撓曲線近似微分方程經過兩次積分可以得到撓曲線方程為

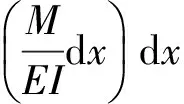
(5)

設分布力的線密度為q，則在分布力范圍內外力偶矩為

(6)

由于懸臂梁的截面是矩形變截面，故橫截面對中性軸的慣性矩為

(7)

則撓曲線的方程為

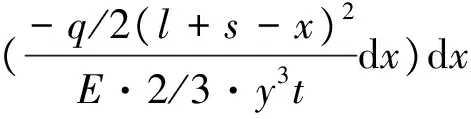
(8)

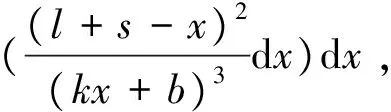
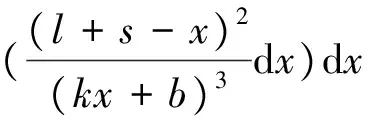
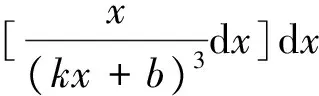
=W+P+Q

(9)

其中：

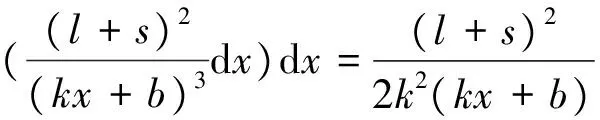
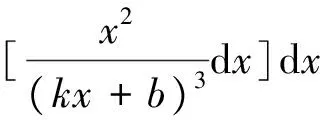
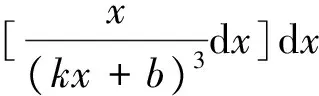
則可得撓曲線方程為

(10)

對撓曲線方程一階求導，可以得到

(11)

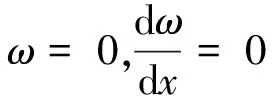
(12)

則可以求得x=l時，懸臂梁的撓度為

ωmax=ωx=l

(13)

以此可得由搖臂變截面懸臂梁的變形引起的轉角變化為

(14)

采用疊加原理，可以得到整個連桿機構的機械剛度的計算方式為

(15)

對以上理論計算方法作以下幾點補充說明：

1)由于把搖臂簡化成懸臂梁計算時忽略了銷孔的存在，而是直接把力加載在懸臂梁的外緣中性面上，所以實際計算的最大撓度值比實際值和仿真的結果相比要小，即最終理論計算的φ2值要小；

2) 與1)同理，轉接桿的理論變形量要比實際測量值和仿真值小，即理論計算的φ3要小；

3) 由于理論計算中沒有考慮銷的變形量和接觸剛度的影響，故最終計算的φ值要小。

綜上所述，運用理論計算的連桿機構的機械剛度值比實際測量值和仿真值要大。實際計算中，由于轉接桿的變形量非常小，故近似認為舵機輸出機構的機械剛度即為連桿機構的機械剛度。

2　作動器輸出機構的剛度優化設計

把理論計算公式通過編程處理，代入常量，改變k或t，可以發現，當|k|或t增大時，變截面懸臂梁的最大撓度越小。因此在輸出機構的實際設計中重點考慮這2個尺寸，以提高輸出機構的機械剛度，圖3所示為作動器輸出機構的兩種不同設計形式。

圖3所示的作動器輸出機構，屬于初步優化設計，考慮到輸出機構有一定的擺角范圍，為防止輸出機構順時針旋轉到最大擺角時，轉接桿與輸出機構軸體發生干涉，需要計算出連桿寬度的最大值。

作動器的零位定義為搖桿在豎直方向時的角度。此處定義機械限位角度為Φ，設輸出機構軸體半徑為R，連桿中心線在坐標系下的斜率為k，連桿的寬度為2d，如圖4所示。

當輸出機構的搖桿剛好達到機械限位時，連桿與滾珠絲杠軸向夾角正切值為

(16)

則連桿中心線在坐標系下的直線方程為

y=k(x+L2cosγ-L1sinφ)+L

(17)

此時，連桿與輸出機構軸體不干涉的條件為

(18)

在實際設計中，綜合考慮各種因素后，選擇雙搖臂的單個厚度為4mm，總厚度為8mm，比改進前輸出機構的搖臂厚2mm，可以在較大程度上改善懸臂梁處的機械變形。另外選擇搖臂的伸展角為50°， 可以較大地減小變截面懸臂梁處受力時的最大撓度。綜合考慮連桿與輸出機構軸體的干涉與搖臂的變形，適當減小搖臂伸展角處過渡弧的半徑為6mm，比原過渡弧半徑少3.5mm。

此外，優化前的設計中，輸出軸體明顯偏長，其伸出軸承了一段距離，這段距離的輸出軸體并沒有對整個作動器的機械剛度或者抗彎曲剛度起到很大的作用，故適當減小其長度，不僅可以減小作動器的質量，還可以給輸出機構的安裝帶來較大便利。

另外，采用齒輪與軸體分離設計，在安裝輸出機構時，可以先安裝軸體，后安裝齒輪，從而達到在不改變現有殼體設計的情況下，順利安裝優化設計后的輸出機構。分離的軸體與齒輪通過沉頭螺釘連接，沉頭螺釘還起到定位的作用。

3　作動器輸出機構剛度仿真分析

對現有的與優化后的作動器輸出機構模型簡化處理后，在Ansys中采用自動劃分網格的方法，定義輸出軸搖臂受到300N·m的負載，得到仿真的結果如圖5所示。

由表1可見，優化設計后作動器輸出機構搖臂處的變形量比優化前減少38.92%，通過計算可得優化設計后舵機輸出軸的機械剛度比優化前提升了63.72%，且質量減小了0.98%。優化后的設計對舵機輸出軸搖臂的底部作了加強處理，起到了加強筋的作用，在一定程度上阻止了搖臂的彈性變形，因此較大地提升了輸出機構的機械剛度。

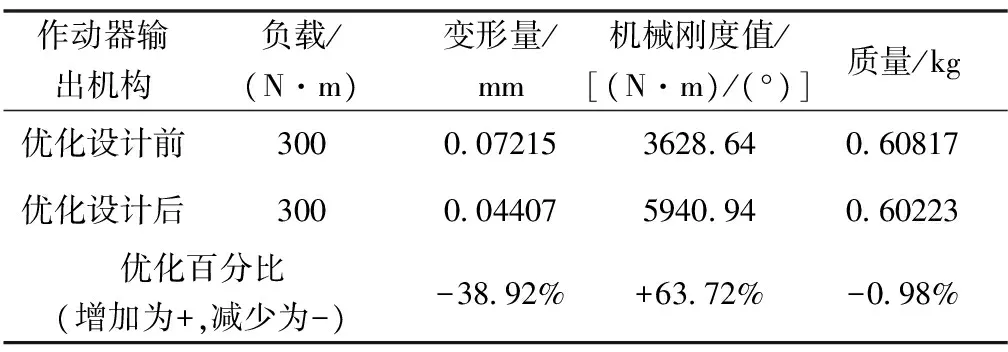
表1　輸出機構優化前后對比

4　結論

1)運用扭轉變形與變截面懸臂梁理論詳細推導了作動器輸出機構的機械剛度計算方法，提出影響輸出機構機械剛度的2個主要因素——厚度和變截面斜率；

2)對作動器輸出機構進行系統地優化設計，在提高輸出機構剛度的同時避免出現安裝干涉與質量增加的情況；

3)通過仿真發現，優化設計后，作動器輸出機構的機械剛度得到了較大的提升，有效地提升了作動器的整體機械剛度，具有較高的實際工程應用價值。

[1]張新榃, 吳志剛, 楊超. 考慮舵機動態特性的顫振分析[C]// 第十一全國空氣彈性學術交流會. 2009.

[2]吳娟, 張家盛, 康光會. 舵機系統動剛度的分析研究[J]. 科學技術與工程, 2008, 8(4):1124-1128.

[3]何锃. 理論力學[M]. 武漢: 華中科技大學出版社，2007.

[4]張盛楠. 電動伺服系統非線性建模、仿真與測試技術[D]. 北京自動化控制設備研究所, 2011.

[5]劉源, 王永樂, 曹東海,等. 一種伺服機構剛度計算方法[J]. 導航定位與授時, 2014, 1(2):46-49.

[6]Lin Y, Baumann E, Bose D M, et al. Tests and techniques for characterizing and modeling X-43A electromechanical actuators[R]. NASA/TM-2008-214637. 2008:21-27.

[7]Layton D S, Gaines V G. F-22 Actuator Dynamic Stiffness (Impedance) Testing[C]// 48thAIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. 2007: 1792.

[8]張新華, 黃建, 張兆凱,等. 大慣量下電動伺服機構非線性特性與控制方法研究[J]. 導航定位與授時, 2017, 4(2):41-47.

[9]張新華，楊瑞峰.含間隙的電動伺服機構非線性振蕩研究[C]//第五屆全國振動利用工程學術會議暨第四次全國超聲電機技術研討會, 2012:825-828.

[10]李友年, 陳星陽. 舵機間隙環節對控制系統的影響分析[J]. 航空兵器, 2012(1):25-27.

[11]李曉貞, 朱如鵬, 李政民卿,等. 齒面摩擦對面齒輪傳動系統振動特性的影響分析[J]. 振動工程學報, 2014, 27(4):583-588.

[12]張勁夫, 許慶余, 張陵. 考慮連桿柔性和運動副粘性摩擦的曲柄滑塊機構的動力學建模及計算[J]. 航空學報, 2001, 22(3):274-276.

[13]肖前進, 賈宏光, 章家保,等. 電動舵機伺服系統非線性辨識及補償[J]. 光學精密工程, 2013, 21(8):2038-2047.

[14]夏棟.電動舵機伺服機構動力學特性研究[D]. 哈爾濱:哈爾濱工業大學, 2014.

[15]李會娜, 高慶, 肖健,等. 空氣舵-伺服系統動態特性試驗技術研究[J]. 強度與環境, 2013(2):7-11.