基于公眾參與行為的化工企業監管治理演化博弈分析*

王循慶,孫曉羽

(山東工商學院 公共管理學院，山東 煙臺 264005)

0　引言

隨著我國化工行業的不斷發展，更多的化工產品被運用到社會生活和生產中，促進了國民經濟的快速發展。然而，由于大多數化工產品具有易燃、易爆、毒害、放射性等危險特性，在生產、儲運和使用過程中，若處置不當,易發生重大安全事故，進而造成嚴重的人員傷亡、財產損失和環境污染等。如2013年6月2日，中石油大連石化分公司發生儲罐爆炸事故，造成4人死亡，直接經濟損失697萬元；2015年9月18日，河南平頂山中鴻煤化公司發生合成爆炸，致使氨泄漏，造成廠區附近20名人員中毒；2016年12月5日，洛陽市高新區洛陽智邦石化設備有限公司發生一起液化石油氣爆炸生產安全事故，造成1人死亡、5人受傷。以上這些化工生產安全事故暴露出化工行業的安全管理與安全監管尚存在較多問題需要解決，因此，對化工行業企業開展安全監管治理問題研究具有重要的現實意義。

化工企業生產安全事故頻發的一個重要原因是安全監管體制還不健全，即在化工產品的生產、運輸、存儲、使用等環節存在嚴重的監管縫隙，導致監管漏洞[1-2]。Wachter和Yorio[3]從企業內部安全管理角度，分析了安全生產監管制度的建立對員工行為的影響；Makin和Winder[4]指出，提高政府的監管力度能夠對企業的安全生產產生重要影響，并分析了外部環境對提升安全生產管理水平的作用；師立晨等[5]指出，危險化學品存在政府監管和企業管理界限不清晰的問題，同時重大危險源建設項目公眾參與不足；Smith等[6]提出，需要加強企業從事危險工作員工的安全培訓和指導，及時監測和識別易受到傷害的員工信息。從博弈論的角度，化工企業安全生產涉及多個利益主體，針對參與主體的利益博弈問題，現有研究主要借助博弈理論分析企業安全生產監管問題。沈斌[7]基于博弈模型分析政府安監部門監管效果，認為政府安監部門在企業發生生產安全事故后進行的處罰金額大小對演化效果的影響比較顯著；劉素霞等[8]在考慮產業集群企業安全生產行為及其監管特點基礎上，通過對企業群體間交互過程的演化模型分析，揭示企業安全生產行為選擇的演化規律。

在實際中，化工企業監管涉及的多方博弈主體具有信息不確定性、有限理性等特點，傳統的博弈理論已不能適用分析。演化博弈理論不同于傳統博弈假設博弈參與者都是完全理性的，而是以具有有限理性的博弈參與者作為分析，開拓了博弈論的一個新研究角度，該理論是由Smith 和Price[9]對生物進化過程現象進行分析時提出的，是具有某種適應性學習能力的漸近演化過程，適應度高的個體將會被保留下來，并給出了演化博弈理論中的演化穩定策略。Binmore等[10]考慮演化過程中的隨機突變問題，并將個體動態進入種群、退出種群以及模仿等機制進行了綜合探討，由此得到了演化博弈理論中的動態模仿者概念；Sethi[11]考慮到策略被模仿學習的可能性不同，有些策略幾乎很難被觀察，所以會更難被模仿學習，提出了一般化的復制動態方程。由于演化博弈理論克服了傳統博弈理論的局限，將有限理性參與者納入到研究中。因此，運用演化博弈理論分析化工企業監管治理問題更加貼近實際。

盡管上述研究對化工企業安全生產監管治理的影響因素和演化過程進行了大量研究，但現有研究還存在一些不足，主要包括：大多數現有研究主要基于博弈主體完全理性來探討化工企業監管治理問題，缺乏考慮博弈主體的有限理性及主體間的交互影響；已有研究成果大多未考慮公眾的參與行為對化工企業的監督作用，沒有將公眾納入到博弈模型中進行分析。因此，本文針對上述不足，基于公眾參與的角度，將地方政府、化工企業、公眾3方同時作為博弈主體，運用演化博弈理論分析不同博弈主體參與行為策略的演化穩定均衡問題。

1　化工企業監管演化博弈模型建立

1.1　模型假設

在不考慮外部環境因素的條件下，可以將化工企業安全生產監管治理過程看作是地方政府、化工企業、公眾3方博弈的結果。本文的基本假設如下：

1)假設1：地方政府、化工企業、公眾等各個博弈主體均具有有限理性特征。其中，化工企業可以采取重視安全投入或者不重視安全投入2種策略；針對化工企業的安全生產投入情況，公眾可選擇參與監督或者不參與監督2種參與行為策略；地方政府可采取嚴格監管或者不嚴格監管2種策略。多個參與主體博弈過程中，假設化工企業采取重視安全投入策略的比例為α，則采取不重視安全投入策略的比例為1-α，α∈[0,1]；地方政府采取嚴格監管策略的比例為β，則采取不嚴格監管策略的比例為1-β，β∈[0,1]；公眾采取參與監督策略的比例為γ，則采取不參與監督策略的比例為1-γ，γ∈[0,1]。

2)假設2：若化工企業重視安全生產，安全生產的投入成本為cH,化工企業獲得收益為W；若地方政府嚴格監督執法時，政府從化工企業安全生產中獲得收益為R，監管成本為cG；若化工企業不重視安全生產，只要政府部門和公眾任何一方發現化工企業不重視安全生產投入，存在重大安全事故隱患時，則對其不重視安全投入的行為處以罰款S；如果地方政府未采取嚴格監管，公眾參與監督發現化工企業的不重視安全投入行為，對其進行上訪，上級政府將對地方政府的安全監管疏忽行為進行處罰F。

3)假設3：若公眾參與到化工企業的安全生產投入監督，其監督成本為cP，地方政府則對公眾的監督舉報行為進行獎勵，其獎勵為δ。

1.2　博弈收益矩陣

根據以上假設和分析，可以得到化工企業安全生產監管治理過程中，地方政府、化工企業、公眾3個參與主體之間的博弈收益矩陣，如表1所示。

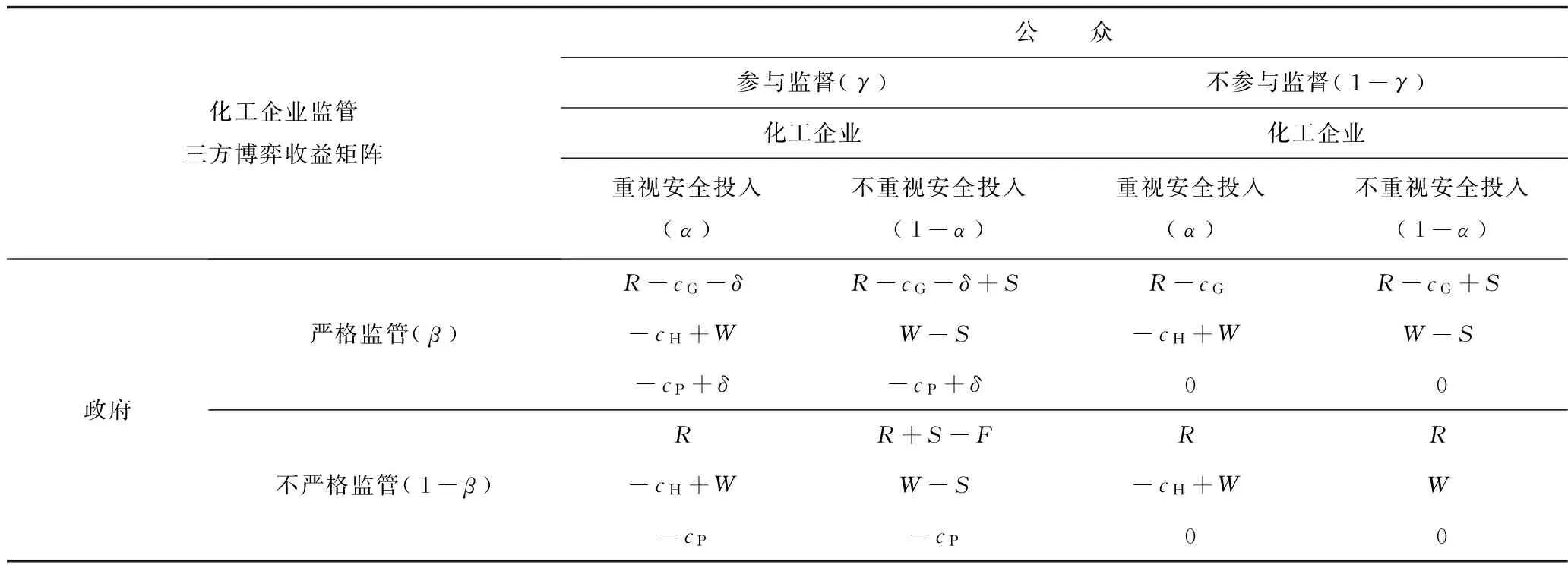
表1　博弈收益矩陣Table 1　Game payoff matrix

2　化工企業監管治理演化博弈均衡分析

2.1　期望收益函數

2.1.1化工企業期望收益函數

基于上文建立的演化博弈模型，可以得到不同策略下的化工企業期望收益。

1)化工企業采取重視安全投入的期望收益為：

V11=βγ(-cH+W)+(1-γ)β

(-cH+W)+γ(1-β)(-cH+W)+

(1-γ)(1-β)(-cH+W)

(1)

2)化工企業采取不重視安全投入的期望收益為：

V12=βγ(W-S)+(1-γ)β

(W-S)+γ(1-β)(-S+W)+

(1-γ)(1-β)W

(2)

3)化工企業的平均期望收益為：

(3)

2.1.2地方政府期望收益函數

同理，可以得出不同策略下的地方政府期望收益。

1)地方政府采取嚴格監管的期望收益為：

V21=αγ(R-cG-δ)+(1-γ)α

(R-cG)+γ(1-α)(R-cG-δ+S)+

(1-γ)(1-α)(R-cG+S)

(4)

2)地方政府采取不嚴格監管的期望收益為：

V22=αγR+(1-γ)αR+

γ(1-α)(R+S-F)+

(1-γ)(1-α)R

(5)

3)地方政府的平均期望收益為：

(6)

2.1.3公眾期望收益函數

同理，可以得出不同策略下的公眾期望收益。

1)公眾采取參與監督行為策略的期望收益為：

V31=αβ(-cG+δ)+(1-β)α

(-cP)+β(1-α)(-cP-δ)+

(1-β)(1-α)(-cP)

(7)

2)公眾采取不參與監督行為策略的期望收益為：

V32=αβ·0+(1-β)α·0+β(1-α)·0+

(1-β)(1-α)·0

(8)

3)公眾的平均期望收益為：

(9)

2.2　博弈的復制動態方程及演化穩定策略分析

由于公眾、地方政府、化工企業等博弈參與主體多表現為有限理性，因此采用演化博弈中的復制動態方程[12-13]來描述其演化過程。

2.2.1化工企業復制動態方程

化工企業的復制動態方程為：

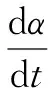
(10)

式中：

F(α)=(-βγS+βS+γS-cH)α(1-α)

(11)

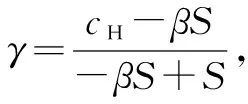
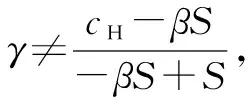
F′(α)=(-βγS+βS+γS-cH)(1-2α)

(12)

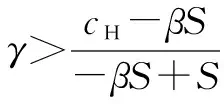
依據以上過程，化工企業的動態趨勢及穩定性如圖1所示。

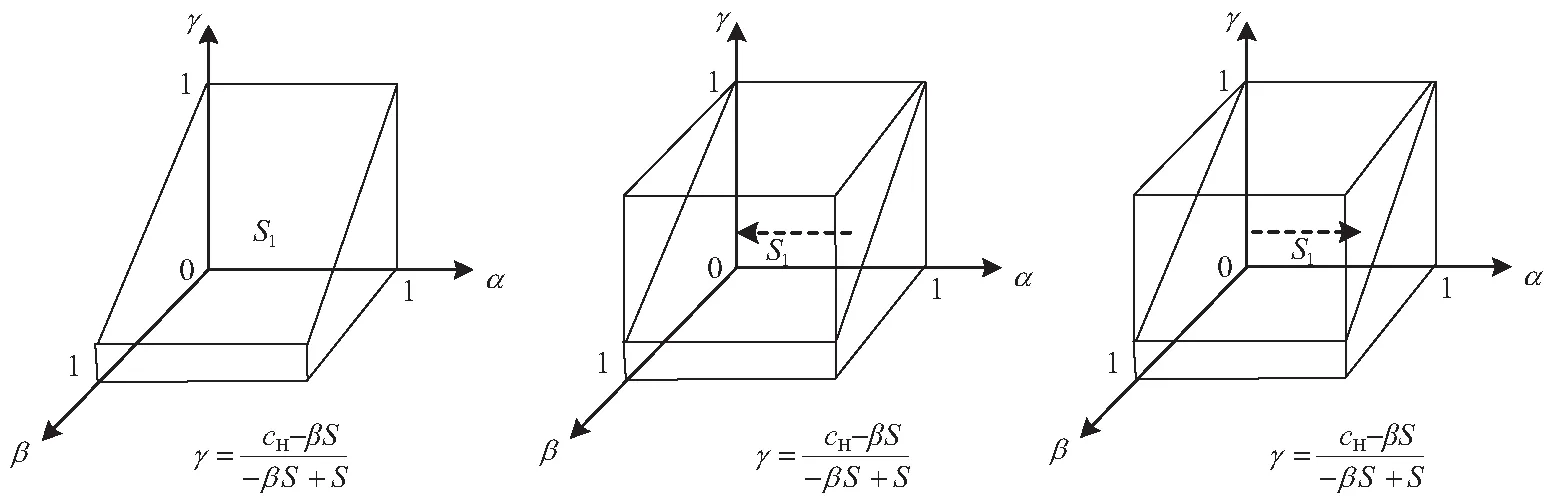
圖1　化工企業動態趨勢示意Fig.1　Dynamic trend of chemical enterprise

2.2.2地方政府復制動態方程

地方政府的復制動態方程為：

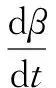
(13)

式中：

G(β)=(αγ(-F+S)+α(-cG)+

γ(-δ+F-S)+(-cG+S))

β(1-β)

(14)

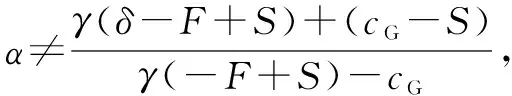
G′(β)=(αγ(-F+S)+α(-cG)+

γ(-δ+F-S)+(-cG+S))

(1-2β)

(15)

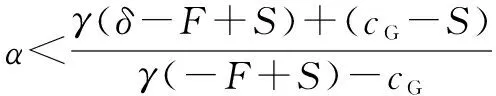
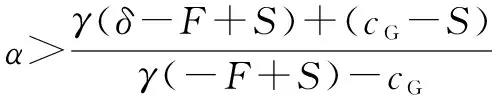
根據以上過程，地方政府的動態趨勢及穩定性如圖2所示。

圖2　地方政府動態趨勢示意Fig. 2　Dynamic trend of local government

2.2.3公眾復制動態方程

公眾的復制動態方程為：

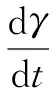
(16)

式中：

H(γ)=(-cP+βδ)γ(1-γ)

(17)

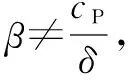
H′(γ)=(-cP+βδ)(1-2γ)

(18)

根據以上過程，公眾行為的動態趨勢及穩定性如圖3所示。

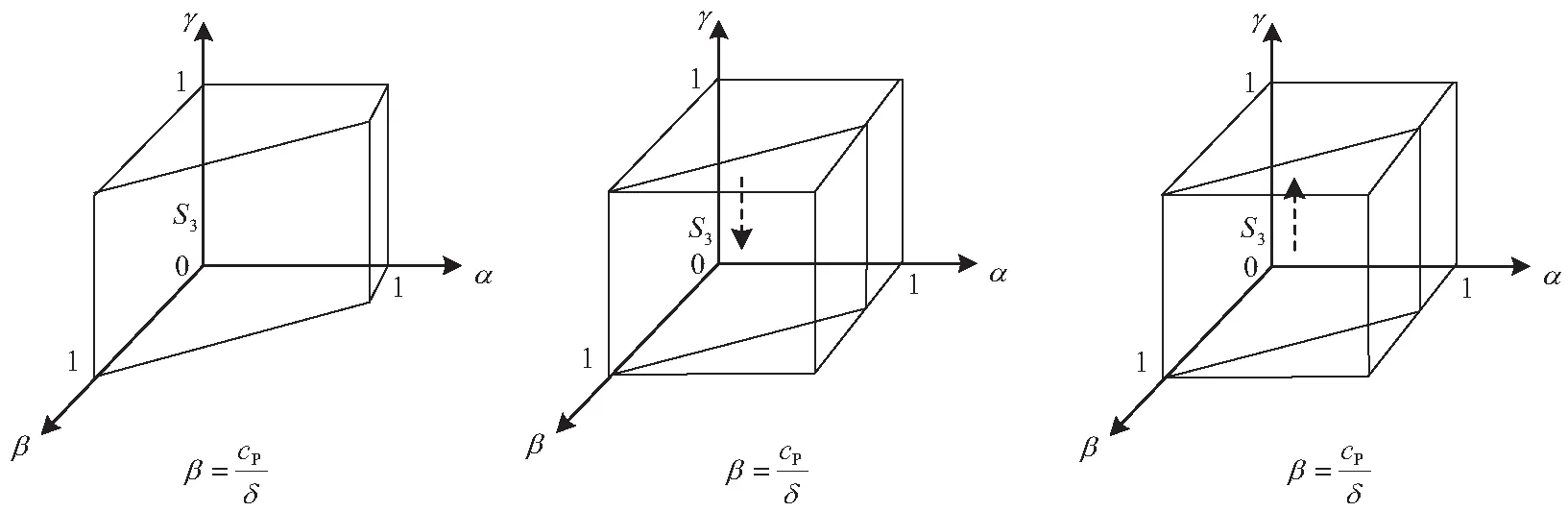
圖3　公眾行為動態趨勢示意Fig. 3　Dynamic trend of public participationbehavior

根據上述3方博弈演化穩定性分析可以得出：

1)化工企業策略選擇的演化穩定狀態受到地方政府嚴格監管的比例β和公眾選擇參與監督的比例γ變化影響；

2)地方政府策略選擇的演化穩定狀態受到化工企業重視安全投入的比例α和公眾選擇參與監督的比例γ變化影響；

3)公眾策略選擇的演化穩定狀態是受到化工企業重視安全投入的比例α和地方政府嚴格監管的比例β變化影響。

由此可以發現，化工企業監管3方博弈過程中，某個博弈主體策略選擇的演化趨勢都與其他2個博弈主體的策略選擇密切相關，這3者的行為是相互作用和影響的。可以通過調整或控制相關變量促使化工企業、地方政府、公眾3方博弈最終演化到重視安全投入、嚴格監管、參與監督的穩定狀態。

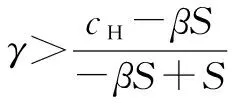
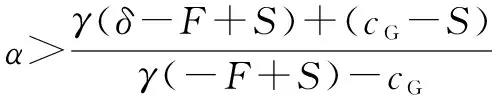
3　混合策略的均衡解分析

由式(11)、(14)和(17)可以得到一個化工企業、地方政府和公眾3方構成的動力系統(I)為：

(19)

依據Friedman[14]提出的方法，其動力系統平衡點的穩定性是根據雅克比矩陣局部穩定性分析得到，系統(I)的雅克比矩陣為：

(20)

根據式(12)的結構特點，系統(I)必然存在8個純策略平衡點，即(0,0,0)，(0,0,1)，(0,1,0)，(0,1,1)，(1,0,0)，(1,0,1)，(1,1,0)，(1,1,1)。這里以平衡點(1,1,1)為例，分析其滿足漸進穩定的條件。系統(I)在平衡點(1,1,1)的雅克比矩陣為：

(21)

矩陣J的特征值為λ1=-s+cH，λ2=-s+δ+2cG，λ3=-δ+cP。若3方共同參與到化工企業安全生產監管治理，此時系統(I)的平衡點(1,1,1)是演化穩定均衡解，則必須滿足條件λ1,λ2,λ3都小于0。由λ1<0，λ2<0，λ3<0，即-s+cH<0，-s+δ+2cG<0，-δ+cP<0可知：當化工企業安全投入的成本小于其不安全投入的罰款，政府的安全監管成本和對公眾監督舉報的獎勵小于政府對不重視安全投入化工企業的罰款，且公眾監督的成本小于其監督舉報的獎勵時，會促使化工企業、政府和公眾3方最終選擇重視安全投入、嚴格監管和參與監督策略，進而最大限度地避免重大化工企業生產安全事故的發生。

4　結論

1)化工企業是否重視安全生產投入很大程度上取決于政府對不重視安全投入化工企業的罰款力度、企業的安全投入成本和政府對化工企業嚴格監管的概率。這需要地方政府通過綜合采用法律和行政手段，對嚴重忽視安全投入的化工企業進行停產、停業等整頓懲處，加大對違規企業的懲罰力度。同時，對重視安全投入的化工企業進行政策支持和獎勵，降低企業安全投入成本。

2)地方政府嚴格監管策略選擇主要取決于政府的監管成本、上級政府的問責力度、對疏忽安全投入企業的罰款。而地方政府部門可以通過運用信息技術手段降低監管成本，與此同時，上級政府要加大對疏忽監管的地方政府的問責力度，提高地方政府的安全生產監管意識。

3)公眾參與監管策略行為的選擇取決于監督舉報的成本和對公眾監督舉報行為的獎勵。這說明可以通過建立多種暢通的投訴渠道(包括網絡平臺、投訴電話等)，降低公眾的監督舉報成本，完善公眾的監督參與機制。此外，對參與監督的公眾給予較高的獎勵，能夠提高公眾參與化工企業安全生產監管治理過程的動力。

4)“地方政府—化工企業—公眾”的3方演化博弈模型可用于分析我國化工企業的安全生產監管治理問題，可為相關監管治理機制的建立提供對策和建議。

[1]佟淑嬌，吳宗之，王如君，等.2001～2013年危險化學品企業較大以上事故統計分析及對策建議[J].中國安全生產科學技術，2015，11(3)：129-134.

TONG Shujiao, WU Zongzhi, WANG Rujun,et al. Statistical analysis and countermeasures on larger and above grades accidents of dangerous chemical enterprises from 2001 to 2013 [J]. Journal of Safety Science and Technology, 2015, 11(3):129-134.

[2]SILVESTRE B S, GIMENES F A, NETO R E. A sustainability paradox? Sustainable operations in the offshore oil and gas industry:The case of Petrobras[J]. Journal of Cleaner Production, 2017, 142(1, SI):360-370.

[3]WACHTER J K, YORIO P L. A system of safety management practices and worker engagement for reducing and preventing accidents:An empirical and theoretical investigation[J]. Accident; Analysis and Prevention, 2014, 68(SI):117-130.

[4]MAKIN A M, WINDER C. A new conceptual framework to improve the application of occupational health and safety management systems[J]. Safety Science, 2008, 46(6):935-948.

[5]師立晨，王如君，多英全.我國危險化學品重大危險源安全監管存在問題及建議[J].中國安全生產科學技術，2014，10(12)：161-166.

SHI Lichen, WANG Rujun, DUO Yingquan. Problems and suggestions of safety supervision of dangerous chemicals major hazard in China[J]. Journal of Safety Science and Technology, 2014, 10(12):161-166.

[6]SMITH P M, SAUNDERS R, LIFSHEN M, et al. The development of a conceptual model and self-reported measure of occupational health and safety vulnerability[J]. Accident; Analysis and Prevention, 2015, 82(8):234-243.

[7]沈斌.基于演化博弈理論的安全生產監管效果研究[J].工業安全與環保，2013，39(2)：68-70, 74.

SHEN Bin.Study on Safety Production Supervision Effect Based on Evolutionary Game Theory[J]. Industrial Safety and Environmental Protection, 2013, 39(2):68-70,74.

[8]劉素霞, 徐建飛, 梅強,等. 產業集群企業安全生產行為演化與監管[J]. 工業工程與管理, 2016, 21(1):52-59.

LIU Suxia, XU Jianfei, MEI Qiang ,et al. Evolution and supervision of the production safety behavior of enterprise in industrial cluster[J]. Industrial Engineering and Management, 2016, 21(1), 52-59.

[9]SMITH J M, PRICE G R. The Logic of Animal Conflict[J]. Nature, 1973, 246(11):15-18.

[10]BINMORE K G, SAMUELSON L, VAUGHAN R. Musical Chairs:Modeling Noisy Evolution[J]. Games & Economic Behavior, 1995, 11(1):1-35.

[11]SETHI R. Strategy-Specific Barriers to Learning and Nonmonotonic Selection Dynamics [J]. Games & Economic Behavior, 1998, 23(2):284-304.

[12]WU Dan, ZHOU Liang, CAI Yu-eming, et al. Energy-Aware dynamic cooperative strategy selection for Relay-Assisted cellular networks:an evolutionary game approach[J]. IEEE Transactions on Vehicular Technology, 2014, 63(9):4659-4669.

[13]LIU De-hai, XIAO Xing-zhi, LI Hong-yi, et al. Historical evolution and benefit-cost explanation of periodical fluctuation in coal mine safety supervision:An evolutionary game analysis framework[J]. European Journal of Operational Research, 2015, 243(3):974-984.

[14]FRIEDMAN D. Evolutionary Games in Economics[J]. Econometrica, 1991, 59(3):637-666.