基于高中數學抽象核心素養下信息技術融入課堂教學案例反思*
李樹森
(江西省南昌縣蓮塘一中 江西南昌 330200)
一、利用信息技術提升數學核心素養的誤區及思考
1.當前課堂教學中信息技術的應用陷入誤區
課堂教學中信息技術的應用正在不斷推廣和普及,現在眾多學校都建設了多媒體教室,越來越多的教師開始通過PPT課件、微課、翻轉課堂等嶄新的信息技術手段開展教學,然而當前課堂教學中信息技術的應用陷人了誤區:部分教師將整堂課變為PPT課件演示的課堂,缺乏必要的板書;當前課堂教學中信息技術的應用,大多是用多媒體代替黑板和粉筆,僅僅實現了教學手段的信息化,沒有真正實現課堂教學與信息技術的深度融合,這就導致在數學課堂中應用信息技術純粹是白費功夫。
2.合理利用信息技術來提升學生數學核心素養思考
數學課堂教學的信息化應該體現在通過利用信息技術引導教師進行信息化教學改革,構建動態化、生活化的數學情境,拉近數學課堂教學和生活實際之間的距離,培養學生學習數學的熱情,并引導學生學會利用幾何畫板、超級畫板、數學解題軟件、數學工具來解決數學問題,讓學生學會數學繪圖、數學建模,提升學生數學核心素養。
二、課堂教學中利用信息技術提升學生數學核心素養途徑與案例
1.信息技術幫助學生直觀形象理解數學概念,提升數學抽象核心素養
數學概念教學是教學重中之重,而得出數學概念的過程是最典型的數學抽象過程,然而教師往往因為技術條件和種種客觀條件的限制,通常只對概念做簡單的介紹和必要的說明,借助于一些信息工具通過數學實驗、課堂觀察、操作體驗等做法可以讓不同層次的學生更有效地參與到課堂中來,這樣講原來很難講清楚的概念,在借助信息技術手段,變得比較直觀,從而提升了學生的數學抽象素養。
案例一、導數的幾何意義
案例說明:導數的幾何意義,雖然可以借助代數的推導,由于導數的幾何意義的概念抽象,動態問題很強,學生理解其幾何意義感到突兀和疑惑,對此,如來設計一些演示性實驗,學生可以很好地理解和接受。
①在幾何畫板中任意作出曲線y=?(x)=x2,繪制定點P(1,1),在離點P遠處任取一點P1,計算此時點的P1橫坐標2.90,同時度量此時直線PP1的斜率為3.90,
②作出曲線y=?(x)=x2在點P(1,1)的切線,度量其切線斜率斜率為2,
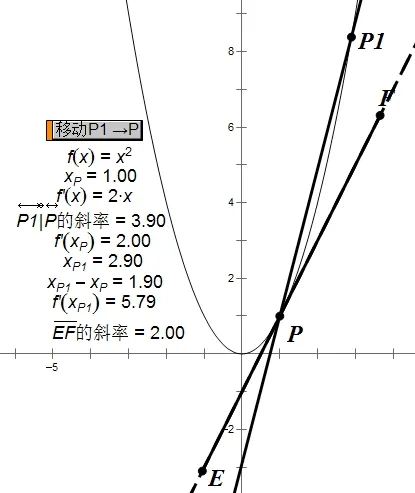
③定義函數?(x)=x2的導函數并計算?′(x)=2x在x=1處的導數?′(1)=2,④計算此時兩個點P,P1的橫坐標之差為2.90,運動點P1→P,通過動畫觀察兩個點的橫坐標之差逐漸減少,最終結果為0,而此時直線PP1與切線重合,其斜率值為2,觀察結果等于?′(1)=2
解導數的幾何意義概念抽象同時具有動態過程,我們可以在坐標系中先作出一條曲線,接著在曲線上選取一個定點。然后在距離P點比較遠的地方選取點P1度量直線PP1的斜率;兩拖動點P1向點P靠近,在這個過程中依次度量每條直線的斜率那么當點Pn無限趨近于點P時,kn無限趨近于切線的斜率
因此,函數?(x)在x=x0處的導數就是它在該處的切線的斜率,借助信息技術使得導數的幾何意義的概念直觀而又生動,促進了學生對其概念的理解,提升了數學抽象核心素養。
2.數學基本活動中融入利用信息技術手段提升學生的數學抽象核心素養
高中學生數學基本活動經驗相對操作比較少,缺乏了從嘗試特殊到一般,缺乏了圖形的驗證,而只是就題論題,只是停留在知識的層面上,被動接受,利用信息技術進行數學實驗,通過動態的畫面和快速的運算,使學生主動進入思維的軌道,很自然然地從感性認識上升到理性認識,提升了學生直觀想象核心素養。
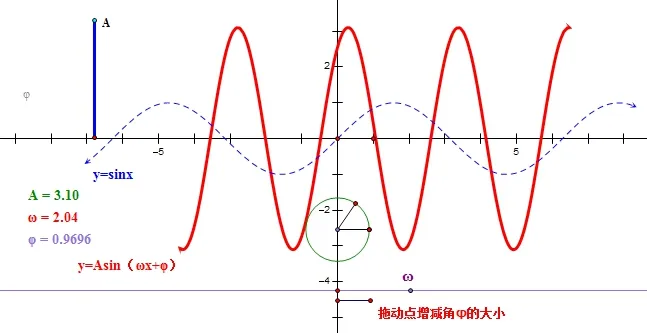
案例二《三角函數圖像y=Asin(ωx+φ)變換》
正弦型函數y=Asin(ωx+φ)是必修4“三角函數”的內容,它可以鞏固正弦函數y=Asin x圖像和性質的學習,也為余弦函數及余弦型函數的學習提供素材。這類函數是函數伸縮變換的特例,也是一般函數圖像變換的基礎。高中數學課程標準對此的要求是,“結合具體實例,了解y=Asin(ωx+φ)的實際意義;能借助計算器或計算機畫出y=Asin(ωx+φ)的圖像,觀察參數A、ω、φ對函數圖像變化的影響”。教師通過幾何畫板演示驗證過程。通過拖動改變A、ω、φ值,使得函數圖像隨之變化,學生直觀形象觀察函數圖像的變化,學生表現出好奇心和興致,突破本節課的難點。
3.運用信息技術創設動態的數學情境,提升學生學習積極性
新課程理念要求我們在教學中創設問題情境教學,因為學生的認知從迫切的需求中開始,思維在疑惑驚奇中啟動,目標從問題情境中導出。 因此在教學中,教師應根據學生的認知規律,挖掘教材,創設有效教學情境,但是有些數學問題的情境常規手段難以做到,例如動態型問題情境,將信息技術融于數學課堂教學,利用多媒體信息技術圖文并茂、聲像并舉、能動會變、形象直觀的特點為學生創設各種情境,能調動學生的學習欲望,激發學習動機和興趣。
綜上所述,隨著科學技術的逐步發展,現代化教學手段在高中數學教學中得到了廣泛的應用,在課堂教學中充分考慮到數學學科的特點,充分將信息技術手段運用到課堂教學中來它給數學課堂教學注入了新鮮的活力,同時也促使數學課堂教學更加直觀化、形象化,從而提升數學核心素養。

