高中數(shù)學(xué)學(xué)習(xí)中如何培養(yǎng)自身建模能力

胡伊淳

（鞏義市第二高級中學(xué) 河南鞏義 451200）

高中數(shù)學(xué)教學(xué)依舊采用傳統(tǒng)應(yīng)試教學(xué)模式，這種教學(xué)課堂不利于我們的數(shù)學(xué)學(xué)習(xí)。據(jù)我的觀察分析，發(fā)現(xiàn)高中生數(shù)學(xué)學(xué)習(xí)的效率非常低下，很多學(xué)生課上、課下非常努力，但是數(shù)學(xué)成績一直不理想。在這種身心具憊的學(xué)習(xí)中，大部分學(xué)生逐漸喪失了數(shù)學(xué)學(xué)習(xí)的興趣與樂趣。我認(rèn)為高中數(shù)學(xué)學(xué)習(xí)首先應(yīng)具備數(shù)學(xué)建模意識，在日常學(xué)習(xí)中提升自己的數(shù)學(xué)建模能力。

一、重視課前問題學(xué)習(xí)，做好課堂學(xué)習(xí)反饋

高中數(shù)學(xué)教材中每一個章節(jié)都有課前導(dǎo)學(xué)問題，因此，在上課之前，我們應(yīng)該自主學(xué)習(xí)導(dǎo)學(xué)問題，明確章節(jié)的重點內(nèi)容，然后在數(shù)學(xué)練習(xí)中利用相關(guān)的數(shù)學(xué)模型解決問題。在課前導(dǎo)學(xué)中，我們會發(fā)現(xiàn)歷史與生活中存在著很多的數(shù)學(xué)知識，當(dāng)我們建立起數(shù)學(xué)學(xué)習(xí)的欲望，久而久之就會產(chǎn)生數(shù)學(xué)建模的欲求。例如，在高中數(shù)學(xué)函數(shù)教材中，導(dǎo)學(xué)問題中有對函數(shù)的物理解釋：物體在進行勻速圓周運動的時候會進行周期性運動；我們家用的電流也在進行周期性變化；一年四季也在進行周期性變化[1]。那么，同學(xué)們?nèi)绾卫脭?shù)學(xué)知識解釋周期性變化的[2]？此時，我們應(yīng)發(fā)動自己的腦筋，結(jié)合課本內(nèi)容提前預(yù)習(xí)周期函數(shù)內(nèi)容，學(xué)習(xí)周期函數(shù)的理論與概念，通過教材中的案例歸納周期函數(shù)的特點等，提前做好課堂學(xué)習(xí)準(zhǔn)備工作。

二、建立完善的數(shù)學(xué)模型

我們要善于利用已經(jīng)掌握的數(shù)學(xué)知識，自行找到影響數(shù)學(xué)解題的主要依據(jù)。在解答數(shù)學(xué)問題時，如果我們發(fā)現(xiàn)問題中僅有一個影響因素，那么我們用一個簡單的公式就可以進行表達(dá)。但是，高中數(shù)學(xué)題中大部分都有很多個未知數(shù)，解題過程中涉及多個未知公式，此時，就需要我們充分聯(lián)系已經(jīng)學(xué)過的數(shù)學(xué)知識，整理相關(guān)知識點給出數(shù)學(xué)模型。

例如，存在多個未知公式的數(shù)學(xué)題，首先，我們應(yīng)該正確找出問題中的影響因數(shù)，根據(jù)題干內(nèi)容和所學(xué)的數(shù)學(xué)知識確定各個未知數(shù)與已知數(shù)之間的關(guān)系，建立起具有關(guān)聯(lián)的數(shù)學(xué)因素模型。在學(xué)習(xí)拋物線函數(shù)的時候，我們可以利用鉛球運動軌跡進行數(shù)學(xué)模型構(gòu)建，通過圖1可以發(fā)現(xiàn)，鉛球拋出的距離y=＝vsin·t－1/2 gt2＋h公式，x＝vcos·t[3]，這就是拋物線方程。在學(xué)習(xí)時，如果我們借助方程組求解，會讓問題變得復(fù)雜。此時，我們可以把這兩個方程有機整合。我們要探討的問題就是鉛球投擲的水平距離L，整個過程如：y=（g/2v2cos2）x2+ tan·x＋h。如果鉛球掉落在地上，此時y＝0，這種情況下方程變?yōu)閥＝（g/2v2cos2）x2+tan·x＋h＝0，此時再引入引入求根公式，可以輕松地求得x＝（v2sin2/2g±[（v2sin2/2g）2＋（2hv2cos2/g）]，在實際生活中y不可能是負(fù)值，因此，我們獲得鉛球的投擲距離模型：L＝（v2sin2/2g）＋[（v2sin2/2g）2＋（2hv2cos2/g）][4]。

當(dāng)我們已經(jīng)找到數(shù)學(xué)課本導(dǎo)學(xué)問題中的影響因素之后，此時，我們就可以將現(xiàn)實中的問題轉(zhuǎn)化成數(shù)學(xué)函數(shù)，運用我們學(xué)過的數(shù)學(xué)知識，將未知的函數(shù)變?yōu)橐阎臄?shù)學(xué)公式，通過函數(shù)解決方式獲得因素逐漸的關(guān)系。 這就是影響問題的函數(shù)公式模型。

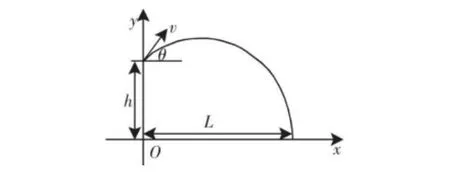
圖1 鉛球運動軌跡示意圖

三、學(xué)會質(zhì)疑，巧設(shè)數(shù)學(xué)問題

想象力大于知識，想象力重于知識，知識的力量是有限的，而想象力則是無限的，想象力可以是世界上所有的事物，想象力推動社會的進步的發(fā)展，是知識進化的本源。因此，在高中數(shù)學(xué)學(xué)習(xí)中，我們應(yīng)具備豐富的想象力，實現(xiàn)數(shù)學(xué)創(chuàng)新教學(xué)，構(gòu)建數(shù)學(xué)學(xué)習(xí)模型。多例高中數(shù)學(xué)學(xué)習(xí)實踐案例證明，高中生的想象力強、新知識與新鮮事物的接受能力強，思維活躍，有很大的創(chuàng)新潛能，這些因素都為我們自身建模能力的培養(yǎng)與提升提供了先決條件。俗話說：“學(xué)啟于思，思源于疑。[2]”心理學(xué)表示，思維意識的培養(yǎng)都是從問題開始的。只有心存疑點，心存問題，才會主動思考辨析，才會學(xué)會創(chuàng)新。學(xué)會質(zhì)疑是高中生數(shù)學(xué)建模能力培養(yǎng)的有效途徑之一。在日常學(xué)習(xí)中，我們應(yīng)多多創(chuàng)設(shè)數(shù)學(xué)學(xué)習(xí)問題，正確提出質(zhì)疑，自行解決問題。我們還應(yīng)多多留意身邊的事物與現(xiàn)象，善于觀察生活中的數(shù)學(xué)問題，加強數(shù)學(xué)模型的應(yīng)用意識與能力。同時，我們還應(yīng)多瀏覽教材以外的數(shù)學(xué)書籍，多做數(shù)學(xué)練習(xí)題，在實際數(shù)學(xué)解題中培養(yǎng)我們的數(shù)學(xué)建模意識與能力。

結(jié)語

總之，數(shù)學(xué)建模是高中數(shù)學(xué)教學(xué)的一個熱門話題，還可以培養(yǎng)我們的自主學(xué)習(xí)習(xí)慣，建立數(shù)學(xué)模型思想，提高高中學(xué)生的創(chuàng)造性思維和發(fā)散性思維，幫助學(xué)生認(rèn)為在多個方面的問題，提高數(shù)學(xué)知識的實際應(yīng)用能力。數(shù)學(xué)建模過程中引入數(shù)學(xué)教學(xué)可以使學(xué)生更加熟悉基本的教學(xué)內(nèi)容，提高學(xué)生解決數(shù)學(xué)問題的能力。