某異形景觀橋人致振動荷載取值及舒適度分析

張雪松，陳永輝，王繼祥

(重慶交通大學 土木工程學院，重慶 400074)

橋梁結構振動，是伴隨著外作用輸入(車輛動荷載、人群動荷載、風力、地震波)，結構體系變形能量和運動能量相互轉換的周期性過程。汽車荷載通過沖擊力系數達到了對車輛靜荷載的放大作用，而沖擊系數由結構固有頻率決定。隨著新型材料與施工工藝的使用，橋梁結構不斷向著大跨、懸挑等更輕柔、阻尼更小的方向發展。對于以人群荷載為主的人行橋，其動力特性較復雜，在人行荷載作用下，會發生一定程度的振動，使人產生不舒適感。通過建立動力學數學模型，采用時域法或頻域法分析人體不同部位對外界振動的響應[1]。故如何使橋體在保證強度、剛度和穩定性的同時滿足舒適度要求已成為結構設計的重點、難點。

結構振動舒適度評價標準主要分為兩類：計算橋體振動特性，為防止人與人行橋共振，減少行人不舒適感，避免發生危險事故，要求天橋上部結構豎向自振頻率不應小于3 Hz[2]；分析外部荷載激勵下的振動響應，采用傅立葉級數來表示人行荷載激勵[3]。

1　工程概況

1.1　工程概況及結構參數

擬建工程為懸挑式景觀玻璃橋(圖1)，平臺布置于場地陡崖邊緣向外懸挑長度達70 m，采用46根拉索將橋塔與玻璃平臺連接成為空間異形結構，作為旅游觀光設施極具視覺沖擊力。該工程為國內最大跨度懸挑景觀橋，其結構自振頻率較低，特殊的結構形式決定了在人行荷載激勵下極易發生共振和行走舒適度較差等問題。玻璃橋主要結構為鋼管、鋼箱梁、鋁合金挑梁、玻璃，主要結構參數見表1。

圖1　成橋效果Fig. 1　Bridge effect diagram

表1　主要結構參數Table 1　Main configuration parameters

1.2　橋體振動特性

新型材料及異形結構形式易引起人群舒適度較差等問題。故需要對景觀橋進行人致振動分析，并評估其舒適度級別，并依此提出相應的減震措施。初步設計階段通過改變截面或結構形式以提高全橋整體、局部剛度，從而減少活載變形、增大自振基頻。從活載撓度、動力特性兩個方面對比以下結構形式：

1) 原結構(主橋部分鋼管采用φ0.4×0.025)；

2) 主橋所有鋼管均采用φ0.4×0.025；

3) 在原結構形式上，拉索直徑修改為7.5 cm；

4) 所有鋼管采用φ0.4×0.025，拉索直徑為7.5 cm；

5) 優化后結構(在原結構主橋頂面、底面做平聯)如圖2，其交叉線條即為平聯結構。

圖2　優化后主橋效果Fig. 2　Main bridge effect diagram after optimization

表2　不同方案結構響應匯總Table 2　Summary of structure response of different programs

筆者通過對主橋結構形式優化：頂、底面增加平聯桿件使其成為“封閉箱梁”形式，增大全橋抗扭剛度，玻璃橋自振頻率增幅明顯，活載變形大大減小。但全橋豎向自振頻率仍小于3 Hz，無法滿足要求；若仍采用豎向結構基頻控制大跨人行橋設計則顯得較為嚴格。同時研究表明：在一定情況下，即使結構基頻落入人群振動敏感區時，也可滿足人群舒適度要求[4]。在結構響應中：振動位移、速度和加速度這3要素，加速度對人生理和心理感受影響最大，直接決定了人行走舒適度，因而建議采用振動響應加速度進行舒適度評價。加速度參數在實際工程中有廣泛應用，如橋梁基礎沖孔樁施工中引進地表振動加速度，以分析沖擊能對振動速度的影響[5]。

人行荷載作為一種動力荷載，是人行橋振動最主要的激勵來源，步行荷載動力特性是影響結構振動分析精度與振動控制效果最主要的因素。由于行人具有自主性，其在橋面上分布具有隨機性，故人行荷載模擬是當前世界范圍內人行橋研究的難點。國外學者已對人群荷載取值做了相應要求，由于國內人群身高、體重等特征參數與西方國家人群有較大差異，直接采用國外人群荷載取值必將引起較大誤差。因此，以國人體質為基礎，建立和研究人群荷載模型，具有必要性和迫切性。

2　步行力產生原理及特點

2.1　步行力產生原理

步行，按照生物力學觀點就是人體在行進過程中，全身肌肉都同時參與工作。步行者在行走過程中，身體重心沿復雜的螺旋形曲線向前運動。行走時左、右兩足跟之間的向距離稱為步長，橫向距離稱為橫距。于國內人群而言，成年男性每復步一般為150～160 cm[6]。

行進過程中，人體重心上下、左右擺動，產生豎向周期性荷載激勵，荷載頻率等同于步行荷載頻率。在雙腿交替行進過程中，人體重心會發生“Z”字形左右擺動，產生水平側向動力荷載，其頻率為步頻的一半。任一時刻行人對景觀橋的動力荷載不同，從而產生一個動態的時程力，包括豎向時程力、縱向時程力、橫向時程力。由于豎向時程力對結構影響最大，筆者以該方向時程力進行分析，其余方向時程力類比于豎向時程力。

筆者將人群荷載分解為3個方向分量形式，各方向時程曲線如圖3。其中：圖3(a)為豎向力時程；圖3(b)為橫向力時程；圖3(c)為縱向力時程[7]。由圖3(a)可看出：豎向力時程具有兩個波峰和一個波谷；在人類行進過程中，需雙腿交替運動，兩下肢交替運動，帶動整個身體前進。

圖3　單步力3方向分量的時程Fig. 3　Time history of the three direction component of a single step force

2.2　步行力特點

人行荷載不同于其他可變荷載，具有以下特點[8-9]。

2.2.1顯著的周期性

人行荷載具有明顯的周期性，成年人正常行走時的步頻在1.6～2.4 Hz，豎向力前3階諧波都可能激發橋梁振動；橫向力步行力頻率在3.2～4.8 Hz，橫向力則一般只考慮1階諧波作用。

2.2.2窄帶隨機過程

由于行人荷載的特殊性，其步長、頻率變化程度沒有其他可變荷載(如汽車荷載、地震荷載等)劇烈，步行步長、頻率均是在很窄范圍內隨機分布。當橋上行人較多時，隨著基數增大，必將導致初相位相等的人越來越多，若此時這群人的腳步頻率與橋梁結構自振頻率接近甚至相同時，橋梁就會產生明顯振動，進而影響行人舒適度甚至結構破壞。

2.2.3人橋“互動”

行人即是結構的激振源，又是感受體。若人行橋發生振動，將嚴重地影響到行人的步行舒適性及安全性，部分行人會停下來依靠橋上欄桿來保持平衡，更多人群會通過調整自己步頻、步長等方式來適應橋梁振動和改善自己行走舒適度，這種現象稱為“集體同步”現象[10-11]，這種行為反而會加劇橋梁橫向振動。

3　人行荷載模型

作為人行橋振動的主要激勵來源，人行荷載對人行橋振動機理研究起著至關重要作用，必須建立合理的行人腳步荷載數學模型，F.C.HARPER等[12-13]采用測力板對人行荷載測量做了研究。目前學界建立的單人腳步荷載時域數學模型有兩類：確定性模型和隨機性模型。確定性荷載模型相對簡單，國外在人行橋動力設計中普遍采用確定性模型對結構進行評估。

3.1　單人荷載模型

人行荷載具有顯著周期性，其豎向力和側向力都可用無窮級數(傅里葉級數)的形式表達出來[14]。

豎向步行力模型如式(1)：

(1)

側向步行力模型如式(2)：

(2)

式中：t為時間；W為體重；fp為步行荷載頻率；αvi為第i階豎向力動載因子；αli為第i階側向力動載因子；φvi為第i階豎向力諧波相位角；φli為第i階側向力諧波相位角。

表3羅列了各國學者提出或經試驗測得的各階諧波動載因子。

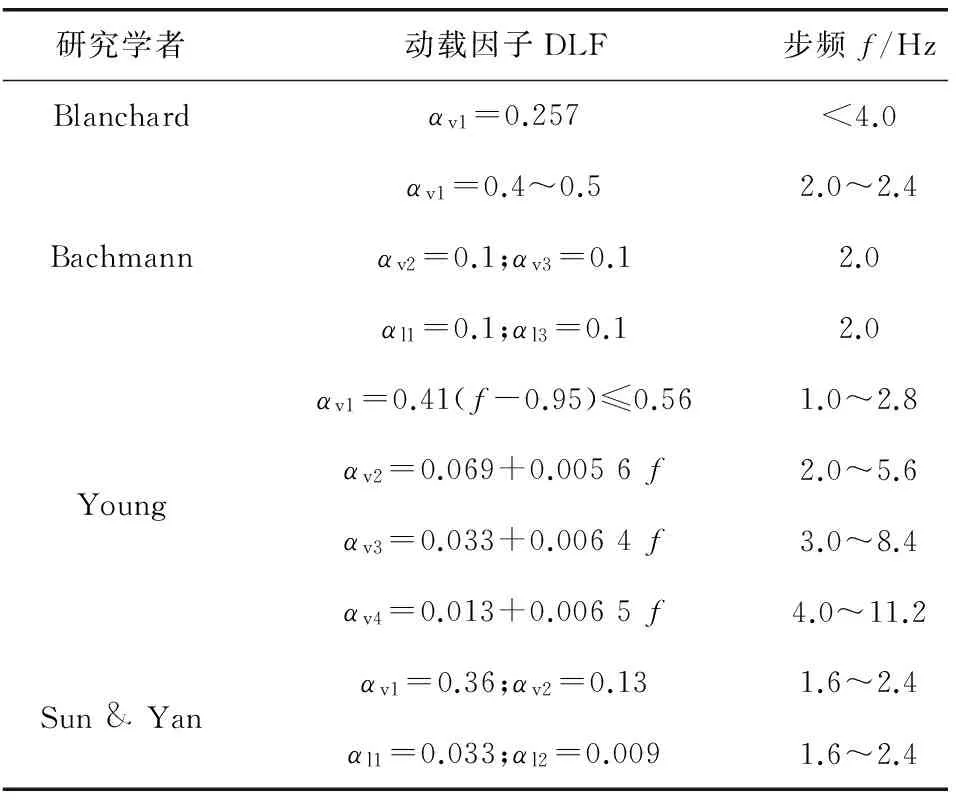
表3　不同學者提出的單人動載因子(DLF)Table 3　Dynamic load factor(DLF) proposed by different scholars

由表3可知：豎向1階諧波動載因子最大，對結構振動貢獻最大，高階諧波動載因子迅速減小，在滿足工程要求前提下只需考慮前3階或前4階動載因子引起的激勵荷載。

3.2　多人荷載模型

多人荷載模型相對于單人荷載模型更為復雜，隨著橋上人數增多，其行走過程的隨機性也逐漸增大。由于人群初相位不同，動力荷載并不能簡單等同于單人動力荷載乘橋上人群總數，而要小于該值。因此不能直接使用單人荷載動載因子，依據表4不同人群密度，人群荷載動載因子α*也有區別。

表4　多人荷載類型劃分Table 4　Partition of multi-person load type

3.2.1小組結伴而行

豎向腳步動荷載的一階諧波分量很容易實現同步，假定小組人群行走完全同步，但2階、3階諧波引起同步的可能性很小，簡化計算時其效應可忽略。人群荷載模型的動載因子與單人荷載的動載因子相同，即α*=α，小組行人步行力模型可用式(3)所采用的單人荷載模型乘以小組人數來計算。

Fp=W·α·sin(2πfp·t)·n

(3)

3.2.2低密度人群自由行走

(4)

3.2.3高密度人群流動

(5)

4　景觀玻璃橋人致振動舒適度分析

玻璃橋采用自振頻率控制設計是不現實的。故筆者采用動力響應評價方法，利用結構在人行荷載激勵下的峰值加速度來對其進行舒適度評價。

動力設計基本過程為[15]：依據結構動力特性，確定敏感頻率范圍；人致振動響應分析，以外界激勵荷載引起結構最大加速度評估舒適性級別，舒適性級別見表5。

表5　人行橋的加速度舒適性判定標準Table 5　Judging criteria of the acceleration comfort of a footbridge

4.1　人群荷載模擬

時程分析法可準確確定在外界荷載激勵下結構內力、位移加速度等響應隨時間的反應，其缺點主要是對計算機配置要求高，計算周期長。時程分析加載形式有固定點加載法、移動加載法，初步設計階段采用固定荷載法計算人群激勵下的最大響應。依據人群活載影響面(線)數據、振型模態，采用等效原則將壓力荷載轉換為節點荷載固定施加在引起最大加速度的點上。

本橋相鄰兩階振型的自振頻率比較接近，且前4階模態均位于活載敏感頻率范圍，故激勵荷載分別采用1.50、1.75、2.00、2.25、2.50、2.75、3.00、3.25、3.50 Hz，以期進行掃頻分析，行人質量取為75 kg，人群密度取1人/m2。選取具有代表性的3個節點：節點1330(主橋右側)、節點1331(主橋左側)和節點1941(主橋最前端)進行分析，分別對比不同頻率激勵荷載作用下各點的豎向加速度值，如圖4。

圖4　時程力加載及觀測點Fig. 4　Diagram of time history force loading and observation points

根據對人行荷載描述，該景觀玻璃橋考慮不利工況為：高密度人群流動。

玻璃橋面寬取用3.8 m，相鄰挑梁間距2.4 m，故面積為3.8×2.4=9.12 m2，相鄰挑梁之間橋上近似為9人。根據表6不同頻率各階動載因子，得出式(6)的等效節點力。

(6)

表6　不同荷載頻率的動載因子Table 6　Dynamic load factor of different load frequency

4.2　動力時程分析

人群激勵荷載頻率為1.5 Hz，人行荷載激勵下選取1330、1331、1941這3個節點的豎向加速度時程，如圖5。

圖5　節點加速度時程Fig. 5　Time history of node acceleration

限于篇幅，筆者不再一一列出其余荷載激勵，對各點在不同頻率下，加速度峰值進行掃頻分析，具體結果見圖6。

圖6　觀測點加速度峰值掃頻分析結果Fig. 6　Sweep-frequency analysis results of acceleration peak values of observation points

5　結論及展望

使用傅立葉三角級數將腳步力等效為外界激勵加載到結構上進行時程計算，對觀測點進行加速度掃描分析，有如下結論：

1) 當增加截面尺寸不能顯著改善結構動力響應時，通過優化部分結構形式可使得活載撓度、自振基頻達到預想結果；

2) 控制結構豎向基頻不應小于3 Hz過于嚴格，必將引起資源浪費。參閱相關文獻，采用各階動載因子參數，將腳步力荷載等效為各階正弦函數代數和的形式。對結構進行動力響應分析，以加速度控制人群舒適度級別；

3) 基于振型模態、活載影響面(線)確定固定荷載加載點，初步設計階段，采用定點加載法比移動荷載法效率更高，且當結構頻率較低時，固定荷載法的結果相對更保守；

4) 由加速度峰值掃描分析結果，驗證了外界激勵等于或接近結構豎向基頻時，振動幅度最大，極易發生共振；

5) 加速度峰值較大時，易引起人群不舒適感，嚴重時會導致橋梁毀壞，建議加裝TMD阻尼器。

參考文獻(References)：

[1]錢凱，胡啟國，李力克.基于人-車-路耦合振動系統的兒童乘坐舒適性[J].重慶交通大學學報(自然科學版)，2013，32(2)：351-359.

QIAN Kai，HU Qiguo，LI Like.Children ride comfort based on human-vehicle-road coupled system of vibration[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2013，32(2)：351-359.

[2]北京市市政工程研究院.城市人行天橋與人行地道技術規范：CJJ 89—95[S].北京：中國建筑工業出版社，1996.

Beijing Municipal Engineering Research Institute.TechnicalSpecificationofUrbanPedestrianOvercrossingandUnderpass：CJJ89—95[S].Beijing：China Architecture & Building Press，1996.

[3]BACHMANN H，PRETLOVE A J，RAINER H.DynamicForcesfromRhythmicalHumanBodyMotions[M].Basel：Birkhause Verlag，1995.

[4]孫滬.異形鋼拱人行橋通行舒適度及其控制研究[D].杭州：浙江工業大學，2015.

SUN Hu.TheResearchonTrafficComfortIndexandVibrationComfortControlofSpecial-shapedSteelArchFootbridge[D].Hangzhou：Zhejiang University of Technology，2015.

[5]佘艷華，蘇華友，肖正學，等.橋梁樁基沖孔樁施工的微振動響應研究[J].重慶交通大學學報(自然科學版)，2011，30(1)：35-38.

SHE Yanhua，SU Huayou，XIAO Zhengxue，et al.Study on the vibration response to punched pile construction of bridge pile foundation[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2011，30(1)：35-38.

[6]錢競光，宋雅偉，葉強，等.步行動作的生物力學原理及其步態分析[J].南京體育學院學報(自然科學版)，2006，5(4)：1-7.

QIAN Jingguang，SONG Yawei，YE Qiang，et al.The biomechanics principle of walking and analysis on gaits[J].JournalofNanjingInstituteofPhysicalEducation(NaturalScience)，2006，5(4)：1-7.

[7]袁旭斌.人行橋人致振動特性研究[D].上海：同濟大學，2006.

YUAN Xubin.ResearchonPedestrian-InducedVibrationofFootbridge[D].Shanghai：Tongji University，2006.

[8]劉軍進，肖從真，潘寵平，等.跳躍和行走激勵下的樓蓋豎向振動反應分析[J].建筑結構，2008，38(11)：108-110.

LIU Junjin，XIAO Congzhen，PAN Chongping，et al.Investigation on response of floor vibration under jumping and walking excitation[J].BuildingStructure，2008，38(11)：108-110.

[9]陳政清.人行橋的振動與動力設計[M].北京：人民交通出版社，2009.

CHEN Zhengqing.VibrationandDynamicDesignofPedestrianBridge[M].Beijing：China Communications Press，2009.

[10]DALLARD P，FITZPATRICK A，FLINT A，et al.The London MillenniumFootbridge[J].StructuralEngineer，2001，79(171)：17-33.

[11]DALLARD P，FITZPATRICK A，FLINT A，et al.London Millennium Bridge：pedestrian-induced lateral vibration[J].JournalofBridgeEngineering，2001，6(6)：412-417.

[12]HARPER F C.The mechanics of walking[J].ResearchAppliedinIndustry，1962，15(1)：23-28.

[13]HARPER F C，WARLOW W J，CLARKE B L.The force applied to the floor by the foot in walking[J].NationalBuildingStudies，1961，12(1)：32-38.

[14]PAVIC A，REYNOLDS P.Vibration serviceability of long-span concrete building floors，part1：review of background information[J].Shock&VibrationDigest，2002，34(3)：191-211.

[15]HIVOS S.GuideLineforDesignforFootbridge[R].U.S.A.：HIVOSS，2007：1-33.