考慮延誤與通行能力的交叉口信號周期優化
王 力,張立立,李 敏,張海波,修偉杰,李正熙
(北方工業大學 城市道路交通智能控制技術北京重點實驗室,北京 100144)
目前,城市道路交叉口信號控制仍以定時控制和感應控制為主。由于受檢測設備完好性的制約以及感應控制策略不適用于過飽和交通流控制的影響,定時控制成為大多數城市交通信號控制首選方法。
控制參數優化設計是定時控制的核心部分。楊錦冬等[1]以延誤最小、排隊車輛數最少為目標,采用YD算法求解最優信號周期;王秋平等[2]建立了以平均延誤時間最短、平均停車次數最少為目標的單點交叉口信號配時優化非線性函數模型,并采用遺傳算法及遺傳模擬退火算法對其進行求解;沈峰等[3]和高云峰等[4]分別將延誤時間、排隊長度、行程時間等指標組成多目標控制,采用NSGA II(none-dominated sorted genetic algorithm II)算法進行優化;臧利林等[5]以車輛平均延誤為優化目標,采用模糊邏輯進行交叉口信號控制策略設計;張本等[6]和劉權富等[7]分別將通行能力與車輛尾氣排放相結合,利用遺傳算法實現交叉口多目標優化;陳小紅等[8]考慮了道路使用率、出行者時間效率以及環境效益之間的協調關系,并結合多目標規劃模型,以通行能力最大、停車率及平均延最小為目標,建立交叉口信號配時多目標優化模型;郭旭明等[9]定義了交叉口旅行時間可靠性,并采用遺傳算法進行優化。唐國磊等[10]通過建立微觀交通仿真模型分析大車混入時飽和流率值和相位損失時間的變化規律,進而推求疏港道路信號控制交叉口通行能力。陳兆盟等[11]利用車頭時距的方差和時間占有率作為判別參數結合周期內排隊車輛的消散,出了一種結合信號控制優化的交通狀態及其真實性的判別方法。
以上研究多是從評價指標(延誤、停車次數、車輛排隊等)或通行能力方面入手對交叉口信號控制參數進行優化,然而對交叉口信號控制分析研究應從通行能力和評價指標兩方面入手,兩者并重。基于此,筆者立足于單交叉口信號控制,通過分析信號周期影響下相位延誤和相位通行能力梯度變化,采用相近函數為目標函數實現對信號周期的優化,能夠使得周期更加適合交叉口的信號控制。
1 相位延誤與通行能力關系分析
相位延誤是交叉口信號控制中重要的評價指標,通過對相位延誤分析可獲知車輛通過交叉口時的受阻滯情況和信號控制效果。車輛在通過交叉口時產生的延誤,主要取決于車輛到達率和交叉口通行能力。相位通行能力是表征相位供需的主要參數,通過相位通行能力可獲知信號控制滿足交通需求程度。對交叉口信號控制分析研究可從相位延誤和相位通行能力之間的關系入手。
筆者以交叉口第K周期內的交通組成和信號控制為例,對無初始排隊交叉口欠飽和、臨界飽和和過飽和情況下的相位延誤和相位通行能力之間關系進行分析。
1.1 單交叉口模型
為便于分析,筆者選取典型兩相位控制單交叉口進行研究,交叉口相位分別為“東西直行”和“南北直行”,如圖1。
其中相位定義如下:
1) 相位1:北直行和南直行的流量分別為q1,3(k)和q3,1(k);
2) 相位2:東直行和西直行的流量分別為q2,4(k)和q4,2(k);
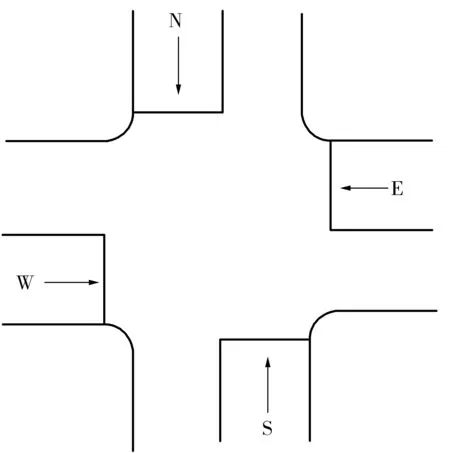
圖1 交叉口相位圖Fig. 1 Intersection phase
為便于簡化參數分析,選擇相向而行的兩個行駛方向中流量較大者作為相位的關鍵流量qi(k),具體定義為:qi(k)=max{qi,i+2(k),qi+2,i(k)},i=1,2。
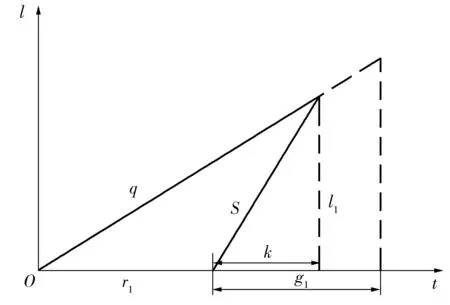
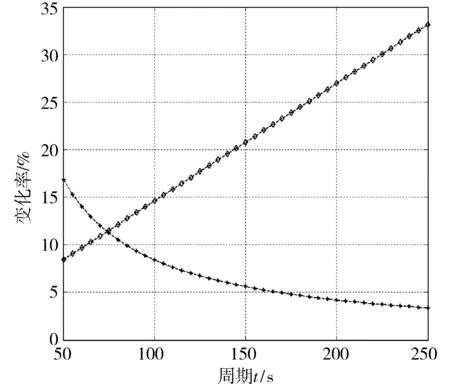
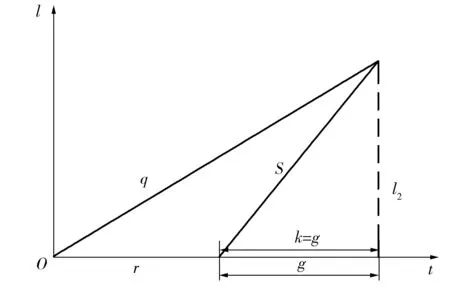
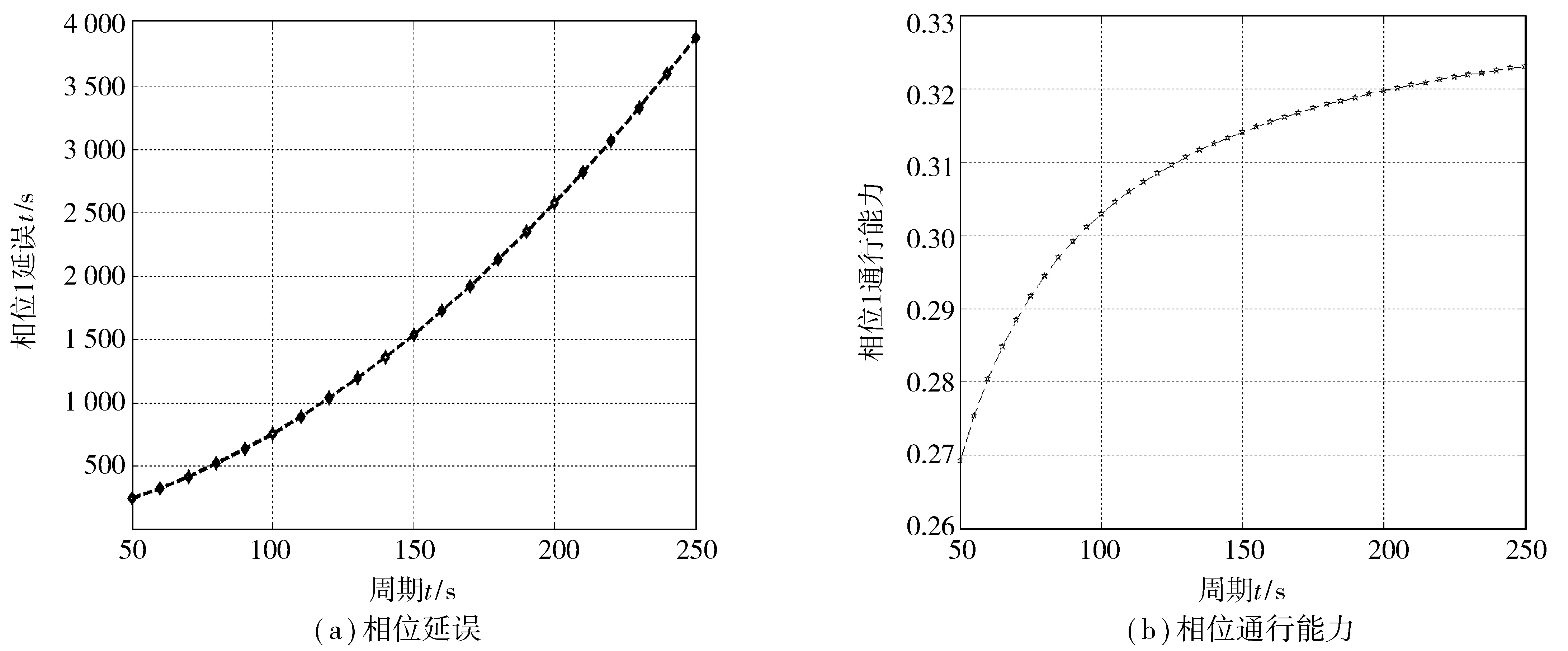
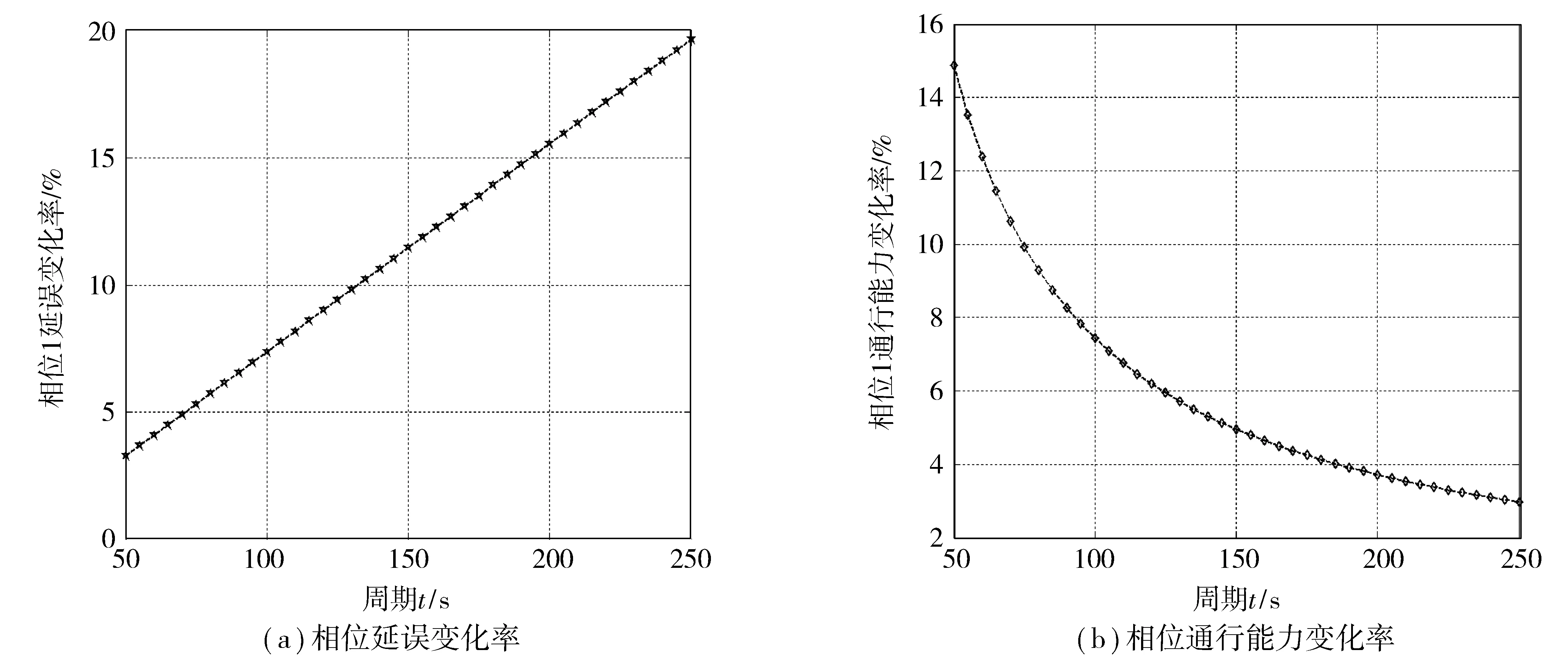
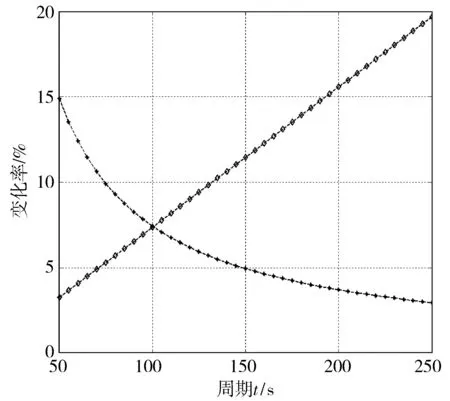
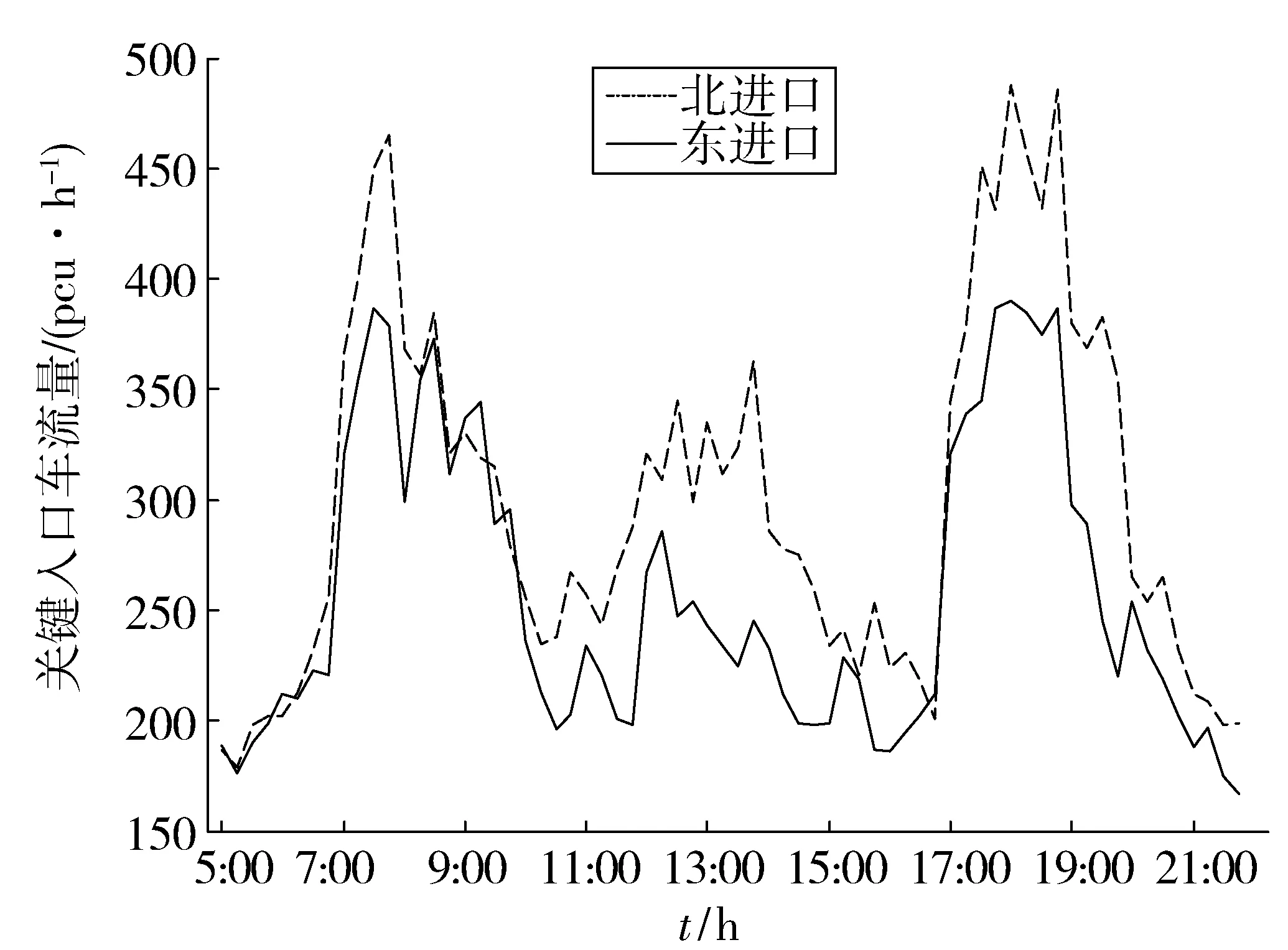
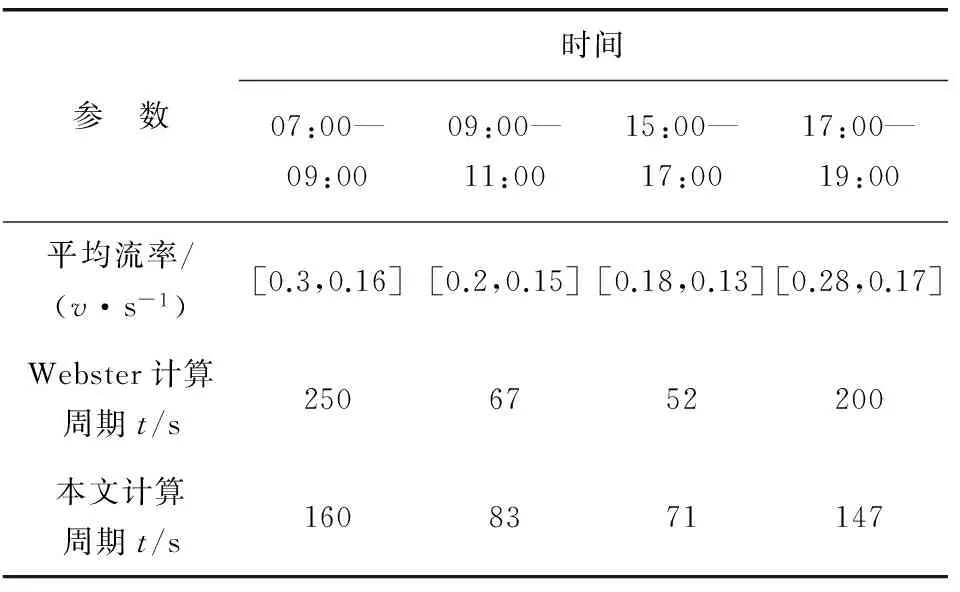
在實際交通流變化中,為避免相位關鍵流量qi(k)在qi,i+2(k)和qi+2,i(k)之間頻繁切換,引入滯回系數h,該系數可由上游交叉口車輛放行情況確定。例如:當連續多個信號周期qi,i+2(k)+h 1.2.1欠飽和狀態下相位延誤與通行能力關系 欠飽和狀態下相位延誤與通行能力關系如圖2,相位1延誤如式(1): (1) 圖2 欠飽和狀態下排隊-時間關系Fig. 2 Queuing-time graph at under saturation state 式(1)可用式(2)表述: (2) 則相位1的通行能力如式(3): (3) 由式(2)、(3)可得: (4) 在欠飽和狀態下,相位延誤和通行能力隨周期變化如圖3。相位流量[q1,q2] 一定條件下,相位1的延誤和通行能力隨信號周期的增大持續增加。 圖3 相位延誤和通行能力隨周期變化Fig. 3 Phase delays and traffic capacity changing with cycle (5) 在欠飽和狀態下,相位延誤梯度和通行能力梯度隨周期變化如圖4。相位流量[q1,q2] 一定條件下,相位1延誤梯度隨信號周期的增大線性增大;而相位1通行能力梯度則隨信號周期的增大持續減小。 圖4 相位延誤梯度和通行能力梯度隨周期變化Fig. 4 Gradient of phase delays and gradient of traffic capacity changing with cycle 圖5是相位延誤梯度和通行能力梯度隨周期變化。由圖5可知:相位1延誤梯度與通行能力梯度在信號周期變化的過程中相交于一點,這為通過梯度分析周期優化帶來便利。 圖5 相位延誤梯度和通行能力梯度隨周期變化Fig. 5 Gradient of phase delays and gradient of traffic capacity changing with cycle 1.2.2臨界飽和狀態下相位延誤與通行能力關系 飽和狀態下相位延誤與通行能力關系如圖6,相位1延誤如式(6): (6) 由式(3)、(6)得: (7) 圖6 臨界飽和排隊-時間關系Fig. 6 Queuing-time graph at critical saturation state 在臨界飽和狀態下,相位延誤和通行能力隨周期變化如圖7。相位流量[q1,q2] 和周期一定條件下,相位1延誤和通行能力為信號周期對應定值。 (8) 圖7 相位延誤和通行能力隨周期變化Fig. 7 Phase delays and traffic capacity changing with cycle 1.2.3過飽和狀態下相位延誤與通行能力關系 過飽和排隊與時間關系如圖8。相位1延誤如式(9): (9) 由式(3)、(9)得: (10) 圖8 過飽和排隊-時間關系Fig. 8 Queuing-time graph at over saturation state 在過飽和狀態下,相位延誤和通行能力隨周期變化如圖9。相位流量[q1,q2] 一定條件下,相位1的延誤和通行能力隨信號周期的增大持續增加。 (11) 在過飽和狀態下,相位延誤梯度和通行能力梯度隨周期變化如圖10。相位流量[q1,q2] 一定的條件下,相位1延誤梯度隨信號周期增大線性增大,而相位1通行能力梯度則隨信號周期增大持續減小。 圖9 相位延誤和通行能力隨周期變化Fig. 9 Phase delays and traffic capacity changing with cycle 圖10 相位延誤梯度和通行能力梯度隨周期變化Fig. 10 Gradient of phase delays and gradient of traffic capacity changing with cycle 圖11是相位延誤梯度和通行能力梯度隨周期變化。由圖11可知:相位1延誤梯度與通行能力梯度在信號周期變化過程中相交于一點,這與圖5中顯示的欠飽和狀態下梯度變化趨勢相同。由此可知:在各種交通狀態下相位延誤梯度與通行能力梯度在信號周期變化過程中都具有相同特性,基于此進行信號周期優化分析具有一定可行性。 筆者的目標是在滿足信號周期最佳范圍條件下,通過尋找相位延誤和相位通行能力梯度變化的最短距離,得到滿足相位流量需求最佳相位延誤和相位通行能力組合,從而實現對信號周期的優化。 圖11 相位延誤梯度和通行能力梯度隨周期變化Fig. 11 Gradient of phase delays and gradient of traffic capacity changing with cycle 以兩相位控制單交叉口為例,其相位延誤表示為:di=[d1,d2];相位通行能力表示為Ri=[R1,Ri、2]。其中:di和Ri可用式(12)、(13)表示。 (12) 約束條件為: (13) 由式(11)、(12),利用歐式距離和平方歐式距離構造函數如式(14): (14) 則有: W(d,R)= (15) 由式(15)可得目標函數,如式(16): J=minW(d,R) (16) Setp 1:利用最速梯度下降算法,分別計算相位i延誤最小梯度和相位i通行能力最小梯度; Setp 2:計算arg min函數定義下的相位i延誤和通行能力; Setp 3:將J=minW(d,R)設為目標函數,對函數變量進行歸一化處理; Setp 4:在周期約束條件下,采用遺傳算法進行優化計算。 圖12 周期優化算法流程Fig. 12 Flow chart of cycle optimization algorithm 為驗證文中所提算法可行性,筆者選取北京市交通學院南路和交大東路交叉口東西和南北兩相位的交通數據進行仿真驗證。該交叉口2個方向05:00—21:00的交通流數據如圖13(每15 min采集1次,折合成小汽車當量)。 為便于與Webster算法進行對比,根據穩態理論,對上述實例交叉口建立如下基本假設: 圖13 交叉口交通流量Fig. 13 Traffic flow at intersection 1) 車輛平均到達率在所取的時間段T之內穩定不變; 2) 所研究的進口斷面,通行能力在相應時段內穩定不變; 3) 車輛受信號阻滯所產生的延誤時間與車輛到達率的相關關系,它們在所取時段T內不變; 4) 在時間段T內,各個信號周期車輛到達率的變化是隨機的,因而車輛在停車線斷面受阻滯排隊長度也是隨機變化的。在某些信號周期內可能出現車輛的到發不平衡,產生過剩滯留車隊。但經過若干周期后,過剩滯留車隊將消失,即就整個時間段T而言,車輛到發始終保持平衡。 表1 信號周期優化Table 1 Signal cycle optimization 圖14 流量-通行能力-延誤關系Fig. 14 Flow-capacity-delay relation diagram 結合表1和圖14可知:當交叉口處于欠飽和狀態時,文中所提算法計算周期所產生的延誤略高于Webster算法;當交叉口過飽和狀態時,由于文中所有算法考慮延誤和通行能力共同約束,故產生的延誤要遠小于Webster算法,由此知筆者所提算法計算所得信號周期能夠更好的適應交通流的變化。計算所得信號周期與李峰等[14]所得結果中的最佳上限相吻合。但在交叉口處于過飽和時,由于考慮了相位延誤和相位通行能力組合關系,并未考慮相位車輛排隊情況,可能造成相位車輛排隊增加,但由于文中重點為信號周期優化,因此將相位車輛排隊影響放在后續工作中進行。 筆者從信號周期與相位延誤和通行能力之間的關系入手,分析了信號周期影響下相位延誤和相位通行能力隨周期變化情況,進而通過分析周期影響下相位延誤和相位通行能力梯度變化,利用歐式距離和平方歐式距離構建了二者的相近函數,并以此為目標函數,采用遺傳算法進行求解。 通過與Webster算法計算結果進行比較,驗證了文中所提算法的有效性。但筆者并未對過飽和狀態下車輛排隊影響進行詳細分析,以及未對其他評價指標與通行能力之間的關系做詳細研究,這些內容將在后續研究工作中逐步完成。 參考文獻(References): [1]楊錦冬,楊東援.城市信號控制交叉口信號周期時長優化模型[J].同濟大學學報(自然科學版),2001,29(7):789-794. YANG Jindong,YANG Dongyuan.Optimized signal time model in signaled intersection[J].JournalofTongjiUniversity(NaturalScience),2001,29(7):789-794. [2]王秋平,譚學龍,張生瑞.城市單點交叉口信號配時優化[J].交通運輸工程學報,2006,6(2):60-64. WANG Qiuping,TAN Xuelong,ZHANG Shengrui.Signal timing optimization of urban signal-point intersection[J].JournalofTrafficandTransportationEngineering,2006,6(2):60-64. [3]沈峰,楊曉光.多目標城市道路交叉口信號配時優化算法研究[J].同濟大學學報(自然科學版),2009,37(7):898-902. SHEN Feng,YANG Xiaoguang.Research on multi-object optimization algorithm of urban road traffic lights[J].JournalofTongjiUniversity(NaturalScience),2009,37(7):898-902. [4]高云峰,徐立鴻,胡華,等.交叉口定周期信號控制多目標優化方法[J].中國公路學報,2011,24(5):82-88. GAO Yunfeng,XU Lihong,HU Hua,et al.Multi-objective optimization method for fixed-time signal control at intersection[J].ChinaJournalofHighwayandTransport,2011,24(5):82-88. [5]臧利林,賈磊,林忠琴.基于模糊邏輯的交通信號控制與仿真研究[J].公路交通科技,2006,23(4):124-127. ZANG Lilin,JA Lei,LIN Zhongqin.Research of traffic signal control and simulation based on fuzzy logic[J].JournalofHighwayandTransportationResearchandDevelopment,2006,23(4):124-127. [6]張本,商蕾,高孝洪.基于遺傳算法的交叉口信號配時多目標優化[J].武漢理工大學學報(交通科學與工程版),2010,34(4):845-848. ZHANG Ben,SHANG Lei,GAO Xiaohong.Traffic intersection signal-planning multi-object optimization based on genetic algorithm[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering),2010,34(4):845-848. [7]劉權富,陸百川,馬慶祿,等.平面交叉口信號控制多目標優化研究[J].交通科技與經濟,2014,16(1):47-50. LIU Quanfu,LU Baichuan,MA Qqinglu,et al.Traffic signal control multi-objective optimization at intersection[J].Technology&EconomyinAreasofCommunications,2014,16(1):47-50. [8]陳小紅,錢大琳,石冬花.基于慢行交通的交叉口信號配時多目標優化模型[J].交通運輸系統工程與信息,2011,11(2):106-111. CHEN Xiaohong,QIAN Dalin,SHI Donghua.Multi-objective optimization method of signal timing for the non-motorized transport at intersection[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2011,11(2):106-111. [9]郭旭明,李瑞敏,張雄飛.基于遺傳算法的交叉口信號控制可靠性優化模型研究[J].公路工程,2012,37(4):44-46. GOU Xuming,LI Ruimin,ZHANG Xiongfei.Traffic signal control reliability optimization based on genetic algorithm[J].HighwayEngineering,2012,37(4):44-46. [10]唐國磊,劉漢卿,王文淵.集裝箱港區疏港道路信號控制交叉口通行能力研究[J].重慶交通大學學報(自然科學版),2016,35(4):133-136. TANG Guolei,LIU Hanqing,WANG Wenyuan.Traffic capacity of signalized intersections on collection and distribution road of container port[J].JournalofChongqingJiaotongUniversity(NaturalScience),2016,35(4):133-136. [11]陳兆盟,劉小明,吳文祥,等.結合信號控制的交通狀態及其真實性判別方法[J].重慶交通大學學報(自然科學版),2016,35(6):95-100. CHEN Zhaomeng,LIU Xiaoming,WU Wenxiang,et al.Identification method of traffic state and its authenticity combined with signal control[J].JournalofChongqingJiaotongUniversity(NaturalScience),2016,35(6):95-100. [12]郝建根,侯忠生,柳向斌.基于多參數規劃的單交叉口排隊長度均衡控制[J].控制與決策,2013,28(4):595-599. HAO Jiangen,HOU Zhongsheng,LIU Xiangbin.Vehicle queuing length balanced-control of the signalized isolated intersection via multi-parametric programming[J].ControlandDecision,2013,28(4):595-599. [13]劉廣萍,裴玉龍.信號控制下交叉口延誤計算方法研究[J].中國公路學報,2005,18(1):104-108. LIU Guangping,PEI Yulong.Study of calculation method of intersection delay under signal control[J].ChinaJournalofHighwayandTransport,2005,18(1):104-108. [14]李峰,王秋平.單點信號交叉口通行能力和服務水平分析[J].城市問題,2003(2):30-33. LI Feng,WANG Qiuping.Analysis of capacity and service level of urban single signalized intersection[J].UrbanProblems,2003(2):30-33.1.2 相位延誤與通行能力關系
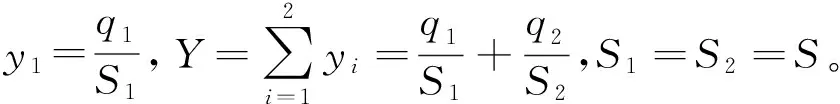
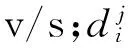

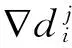



2 周期優化算法
2.1 目標函數


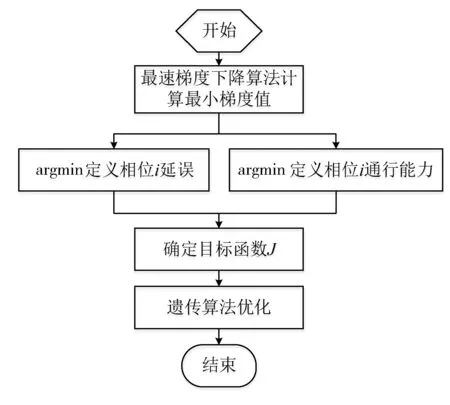
2.2 優化算法(圖12)
3 仿真驗證

4 結 語

