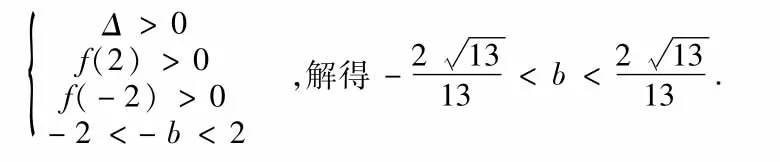熟知知識背景 揭示問題實質
——多角度例說圓錐曲線中的一類對稱問題
◎姚石
角度1 根據判別式及韋達定理來求解
假設兩點A、B關于直線l對稱,根據兩點關于一條直線對稱的知識背景,首先要明確對稱中體現的兩要點:垂直和兩點連線中點在對稱直線l上,因此使用這種方法求解時,必須同時確保:⑴垂直;⑵平分⑶存在,下面就說明三個確保的實施。解法如下:設橢圓上存在A、B兩點關于直線對稱,為了保證A、B兩點所在的直線與直線l垂直,故設直線AB為:則直線 AB與橢圓有兩個不同的交點,即,得:13x2-8nx+16n2-48=0?Δ=-192(4b2-13)>0,解得設點 A(x1,y1)、B(x2,y2),由韋達定理得:,所以A、B兩點中點的橫坐標為縱坐標為,因此點在直線直線l:4x-y+b=0上,即:,解出所以可得:
角度2 根據點差法的知識背景來求解
點差法是解決中點弦的一種常見解題方法,在已知弦中點坐標的前提下,能快速得到弦所在直線的斜率問題,而該題目完全符合點差法的應用條件,解題過程如下:設橢圓上關于直線 l對稱的兩點 A(x1,y1)、B(x2,y2),弦 AB的中點為 M(x0,y0),利用點差法得:在直線l:4x-y+b=0上,得:y0=4x0+b···② ,①②聯立得到x0=-b,y0=-3b,因為點M(x0,y0)在橢圓內部,即
角度3 根據平行弦中點軌跡的背景來求解
根據有關弦中點軌跡的思路,可以通過軌跡曲線與圓錐曲線的位置關系,可利用數形結合尋找參數范圍。解題思路如下:
設橢圓上關于直線l對稱的兩點 A(x1,y1)、B(x2,y2),弦 AB的中點為 M(x0,y0),利用點差法得:,得y0=3x0,所以以為斜率的平行弦的中點軌跡是直線y=3x在橢圓內部的一段(不包括端點)。將y=3x與橢圓聯立得兩交點,所以問題即轉化為直線l:4xy+b=0與線段有交點,易得
角度4 根據根的分布來求解
橢圓上存在不同兩點關于直線l對稱,等價于橢圓上存在被l垂直平分弦,即等價于橢圓的適合條件的弦所在的直線方程,與曲線的方程組成的方程組在某確定的區間上有兩個不同的解,因此可以利用一元二次方程根的分布來解,解題過程如下:根據角度2得到中點M(x0,y0)的坐標為(-b,-3b),直線AB的方程為: