基于規(guī)則提取的決策粗糙集閾值自適應算法*

范兵兵，李 進，陳玉金

（空軍工程大學防空反導學院，西安 710051）

0 引言

決策粗糙集［1］是Yao等人提出的，在經典Pawlak粗糙集［2-3］的基礎上引入了貝葉斯風險分析，通過單個代價矩陣來求得構建概率粗糙近似所需的一對閾值［4］。然而，單個代價矩陣的確定需要合理的先驗知識，不合理的先驗知識將直接導致模型無法獲得具有普遍決策意義的近似集和決策規(guī)則。為了消除或者抑制這種由不合理先驗知識帶來的模型噪聲，許多學者給出了自己的解決方法。文獻［5-7］通過構建多重代價決策粗糙集模型來解決單一矩陣決策的不足；文獻［8-11］通過構建包含模糊概念的代價函數，建立基于模糊概念的決策粗糙集模型，進而抑制不合理的先驗知識帶來的分類不精確性；文獻［12］通過引入博弈論尋求最優(yōu)策略確定閾值；文獻［13］從最小代價角度考慮自適應確定閾值。以上的研究從不同側面推動了決策粗糙集模型的發(fā)展。

回顧決策粗糙集模型和相關的約簡算法，決策規(guī)則的簡潔程度和可信度是模型分類效果好壞的直接體現。因此，在考慮如何抑制由不合理先驗知識帶來的模型噪聲時，需要兼顧考慮模型分類效果好壞：1）在屬性約簡及后續(xù)決策中，可信度高的規(guī)則更具有指導性作用。2）獲取的決策規(guī)則越簡潔，即屬性的個數越少，信息系統(tǒng)決策速率越快。

1 基本知識

1.1 經典決策粗糙集模型

在此基礎上，定義決策粗糙集的下、上近似分別為：

1.2 決策規(guī)則的獲取

2 基于決策規(guī)則的求閾值方法

在決策粗糙集及屬性約簡中，如何通過合理的先驗知識給出合理的風險代價矩陣是一個需要解決的關鍵問題。基于此，本節(jié)介紹一種自適應求代價矩陣的算法，以減少新引入參數對模型的影響。

回顧決策粗糙集模型和相關的約簡算法，決策規(guī)則的簡潔程度和可信度是模型分類效果好壞的直接體現。因此，在考慮自適應求代價矩陣的算法中必須考慮以下兩點：

1）在屬性約簡及后續(xù)決策中，可信度高的規(guī)則更具有指導性作用。

2）獲取的決策規(guī)則越簡潔，即屬性的個數越少，信息系統(tǒng)決策速率越快。

下面我們將基于決策規(guī)則的自適應求代價矩陣方法轉化為單目標優(yōu)化問題進行解決。令為一信息系統(tǒng)，其中，那么，求代價矩陣的問題可以轉化為

同時，為了保留一個明確的邊界域，假設α≥β。綜合以上條件，對約束條件進行簡化

3 基于引力搜索算法的自適應求閾值算法

3.1 引力搜索算法的基本描述

假設存在一個包含N個個體的系統(tǒng)。其中，第i個個體的位置定義為n維空間。那么，t時刻第 d維上，個體 Xj，Xi之間的作用力分量定義為

其中，Maj（t）和Mpi（t）分別為個體Xj和粒子Xi的主動引力質量和被動引力質量。ε是一個很小的常量，防止分母為零；Rij（t）是粒子Xj和粒子Xi的歐式距離；G（t）是在 t時刻的引力常數

其中，G0、α為常數，T是最大迭代次數。文獻［15］建議取值為 G0=100，α=20。

這里假設引力質量和慣性質量相等，即Mai=Mpi=Mii=Mi，i=1，2，…，n。那么，式（3）中的相關質量值可以計算如下

其中，fiti（t）表示t時刻個體Xi的適應度；best（t），worst（t）表示t時刻所有個體最好和最差的適應度值。

Rij（t）通過矩陣范數表示

那么，個體Xi在t時刻第d維上受到的合力為：

其中，randj是［0，1］的隨機數，kbest表示當前質量排名前k位的個體。

根據牛頓第二定律，個體Xi在t時刻第d維的加速度aid（t）為

最后，個體的速度和位置更新如下

其中，randi是［0，1］的隨機數。分別表示個體Xi在t時刻第d維上的速度分量和位移分量。

3.2 自適應求閾值的算法描述

3.2.1 個體位置的表示

第i個個體Xi的位置由一組四維的正實數向量，其中，表示當一個對象x屬于集合X時，采取aB，aN決策時所需的代價表示當一個對象x不屬于集合X時，采取aP，aB決策時所需的代價。同時根據最優(yōu)化問題描述可得，滿足如下關系

3.2.2 適應度函數

代價矩陣的適應度函數需要滿足兩個條件：一是要保證通過代價矩陣得出的閾值可以給出簡潔且有效的決策規(guī)則；二是要保證所有個體都能夠受到力的作用（慣性質量大于等于0），進而發(fā)生位移，以產生新的個體供全局搜索。因此，適應度函數定義為

由于約簡問題中需要求解目標函數的最大值，因此定義

3.2.3 位置修正

由適應度函數可得，引力搜索算法中對于加速度和位移分量的計算結果可能導致個體位置不滿足式（14）的約束，故需要對數據結果進行修正。

閾值α，β的取值事實上可以為一系列離散值代替以往區(qū)間內的連續(xù)值，而使等價類進行正域、負域、邊界域劃分效果不變。例：已知，等價類為，當閾值或者時，均可達到使等價類劃分到正域的效果，同理，對于等價類，當閾值或者時，均可達到使等價類劃分到負域的效果。因此，可以推斷，對于任一等價類，假設其含有n個元素，則當時，可以達到相同的劃分效果。將α，β的取值離散化后，相對于區(qū)間內的連續(xù)值更加適合智能算法的搜索，使搜索時間減少也避免發(fā)生組合爆炸。

本算法引入上述位置修正以及閾值α，β的離散化限定，保證個體位置滿足問題約束，具體如算法1所示。

算法1：代價矩陣位置修正

綜合以上分析，下面給出基于引力搜索算法的自適應求代價矩陣算法，如下頁算法2所示。

4 仿真實驗

為了檢驗上述基于引力搜索的自適應求閾值算法的應用過程和效果，將引力搜索求三支決策最優(yōu)閾值算法分別和自適應算法Alcofa、模擬退火算法求解三支決策閾值從運行時間隨著屬性個數以及樣本數增加，對其運行時間影響兩方面進行比較。此外，為了檢驗利用基于引力搜索的自適應算法學習到的閾值的有效性，利用3種算法學習到的閾值構建了分類器，并計算其準確率Precision（P）、召回率Recall（R）和F1值，計算方法［14］如下：Preciosn=系統(tǒng)檢索到的相關文件數/相關文件總數Recall=系統(tǒng)檢索到的相關文件數/系統(tǒng)返回的文件總數

算法2：基于引力搜索算法的自適應求代價矩陣算法

Step1：系統(tǒng)初始化

1）給定系統(tǒng)中個體規(guī)模N，最大迭代次數T，初始化每個個體的位置

2）根據式（14）、相應的屬性約簡算法和決策規(guī)則提取方法計算每個個體的適應度值fiti（t），記錄最優(yōu)適應度值及對應的個體位置信息作為歷史最優(yōu)信息

Step2：系統(tǒng)位置更新

1）根據式（8）計算每個個體的慣性質量Mi（t）

2）根據式（10）計算每個個體當前時刻受其他個體影響的合力Fid（t）

3）根據式（11）計算每個個體當前時刻的加速度aid（t）

4）根據式（12）更新每個個體的速度和位置

5）根據算法1對新系統(tǒng)中的個體位置進行修正

6）根據式（14）更新每個個體的適應度值fiti（t）

7）記錄當前時刻最優(yōu)適應度值及對應的個體位置信息。若當前時刻最優(yōu)適應度值優(yōu)于歷史最優(yōu)適應度值，則更新歷史最優(yōu)信息

Step3：如果連續(xù)M代最優(yōu)適應度值沒有發(fā)生變化或者迭代次數達到最大迭代次數T，轉到Step4，否則轉到Step2

F1=2Precision x Recall/（ Precision+Recall）

實驗環(huán)境如下：CPU是Intel的I7-4790，主頻3.60 GHz，8G 的內存，64位的 Windows7系統(tǒng)，Matlab R2012a上實現。

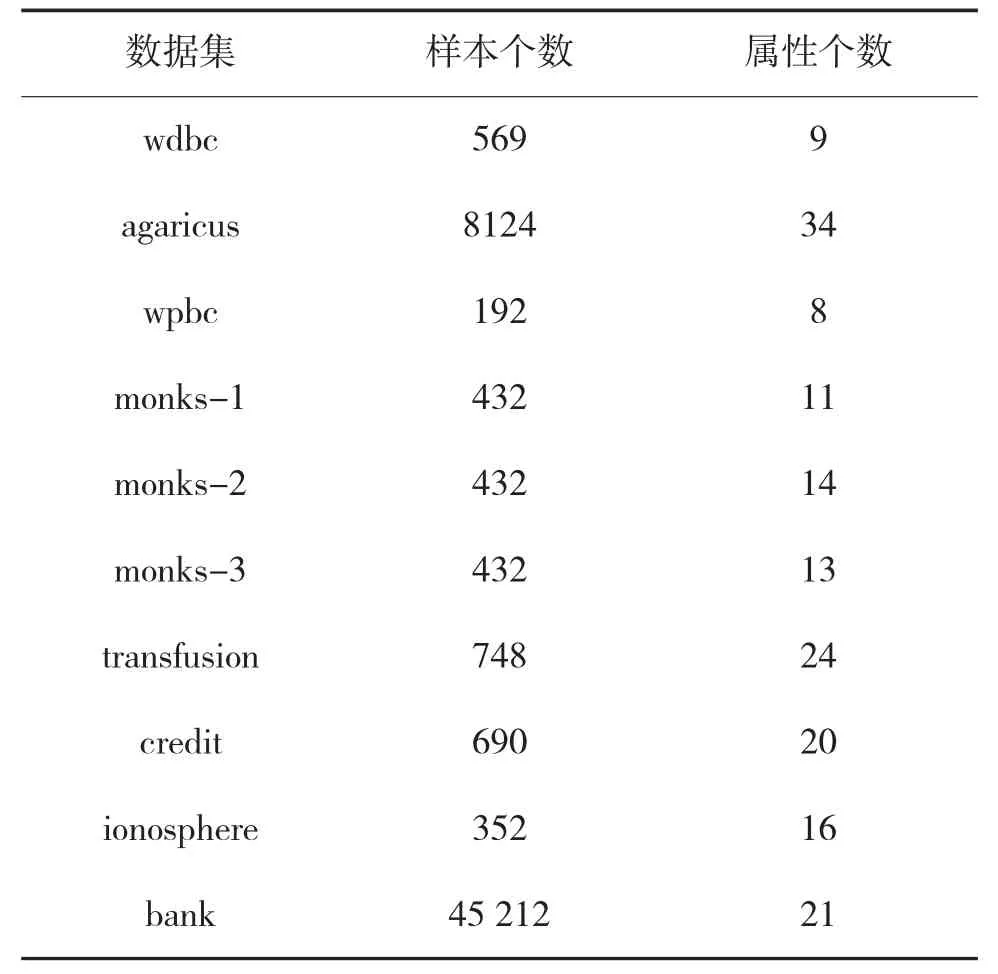
表1 數據集描述

實驗的數據集為UCI數據庫中的10個數據集，首先，需要對數據集進行預處理，將數據集中的missing值直接刪除。又因為模擬退火算法是一種隨機算法，每次運行狀態(tài)和結果可能不一樣，因此，對每個數據集都運行50次取平均值作為算法的運行結果。

從表2中的運行時間結果來看，由于對引力搜索空間進行了離散化的搜索限定，使得引力搜索自適應算法明顯快于自適應算法和模擬退火算法，并且隨著數據集樣本以及屬性的增加，運行時間無明顯增加。而自適應算法Alcofa的運行時間隨著樣本個數以及屬性個數的增加明顯提高。

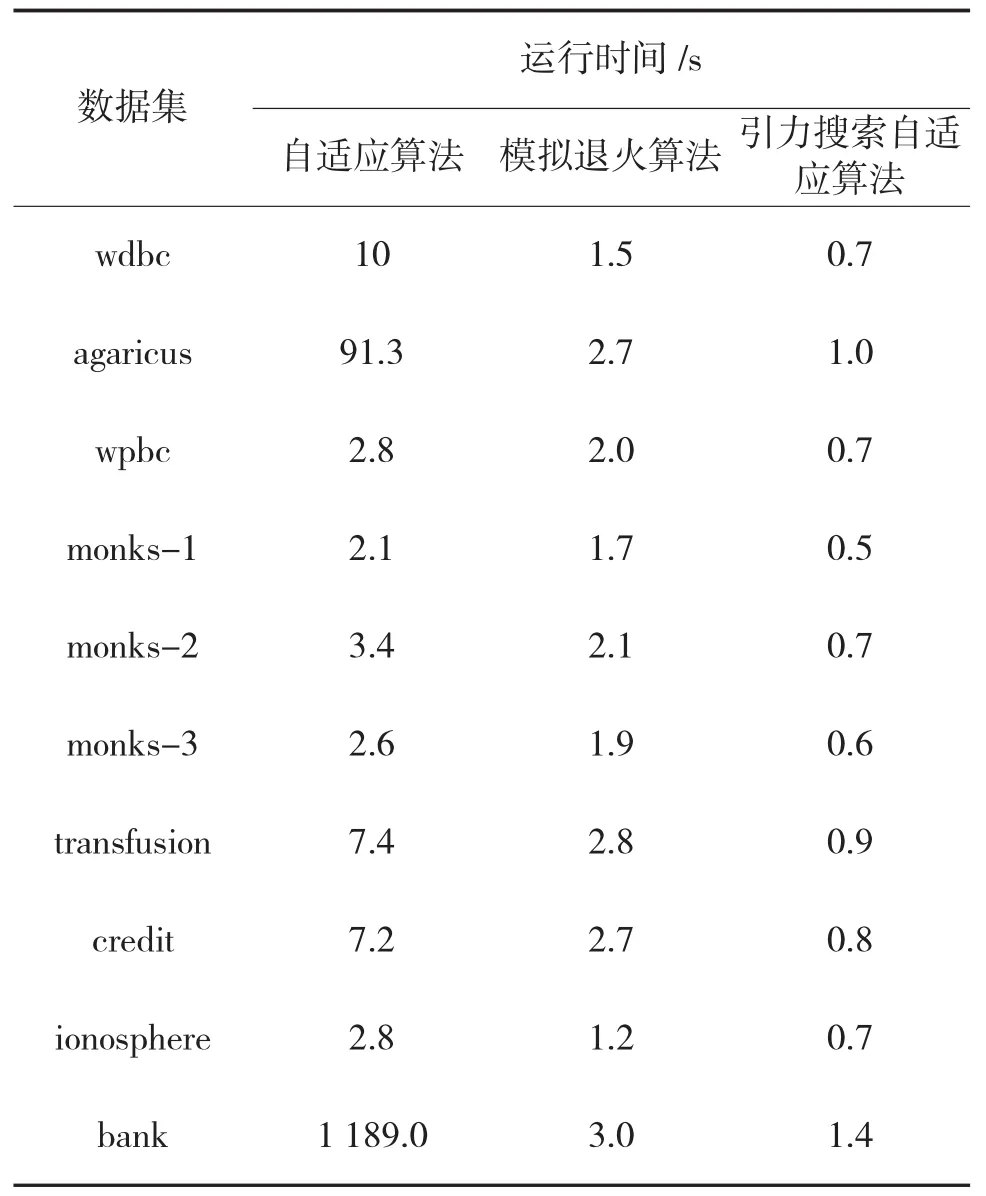
表2 3種算法的運行時間結果

為了研究隨著屬性個數以及樣本數增加對其運行時間影響，分別限定數據集樣本個數固定為432、屬性個數9到34不等，以及數據集樣本個數為192～45 212不等、屬性個數固定為11，對這兩種情況進行實驗，并統(tǒng)計運行時間，如下頁表3所示。

從表3所求的標準差來看，無論是隨著屬性個數增加還是隨著樣本個數增加，引力搜索自適應算法較Alcofa算法以及模擬退火算法均具有更好的穩(wěn)定性。

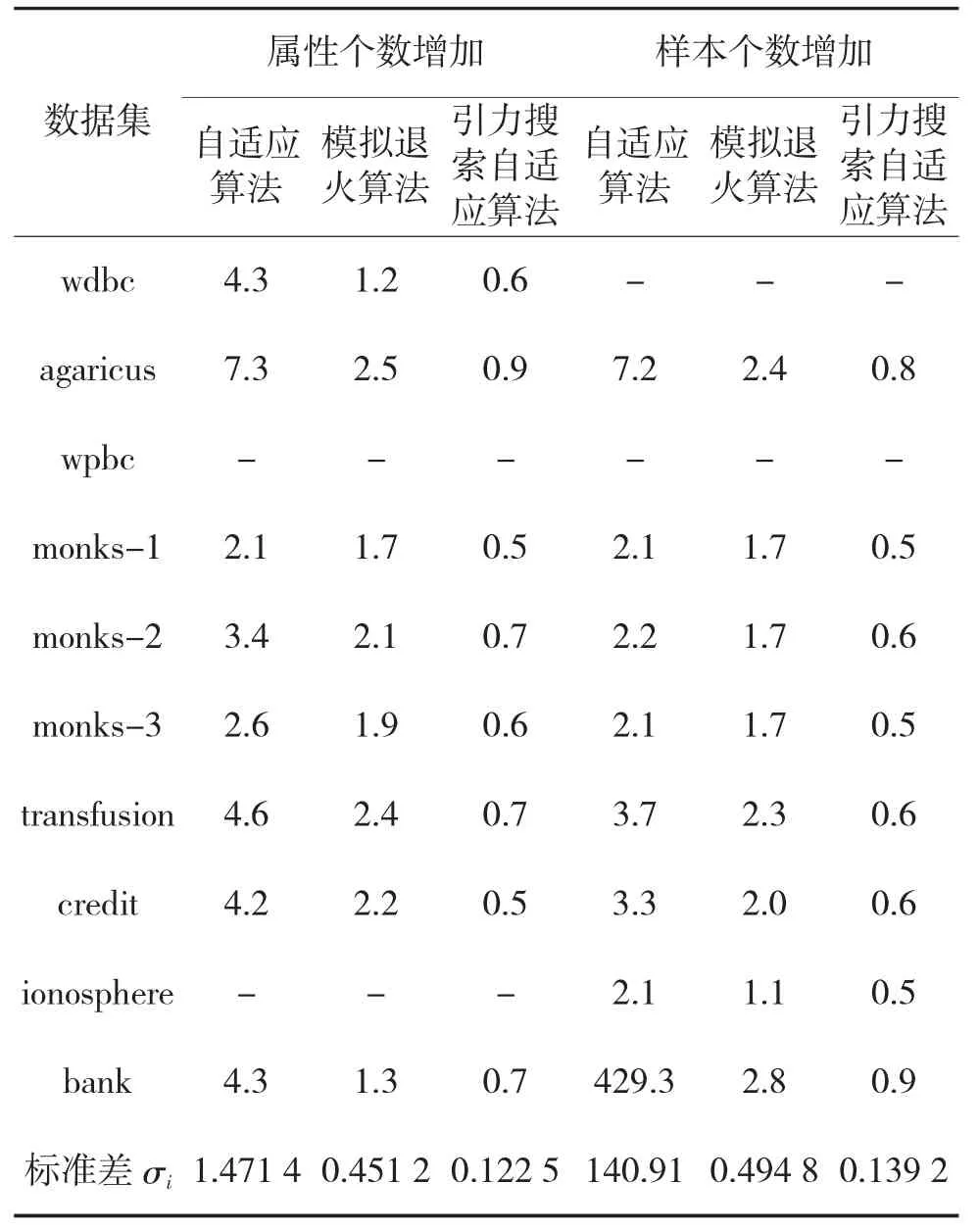
表3 兩種情況的運行時間結果

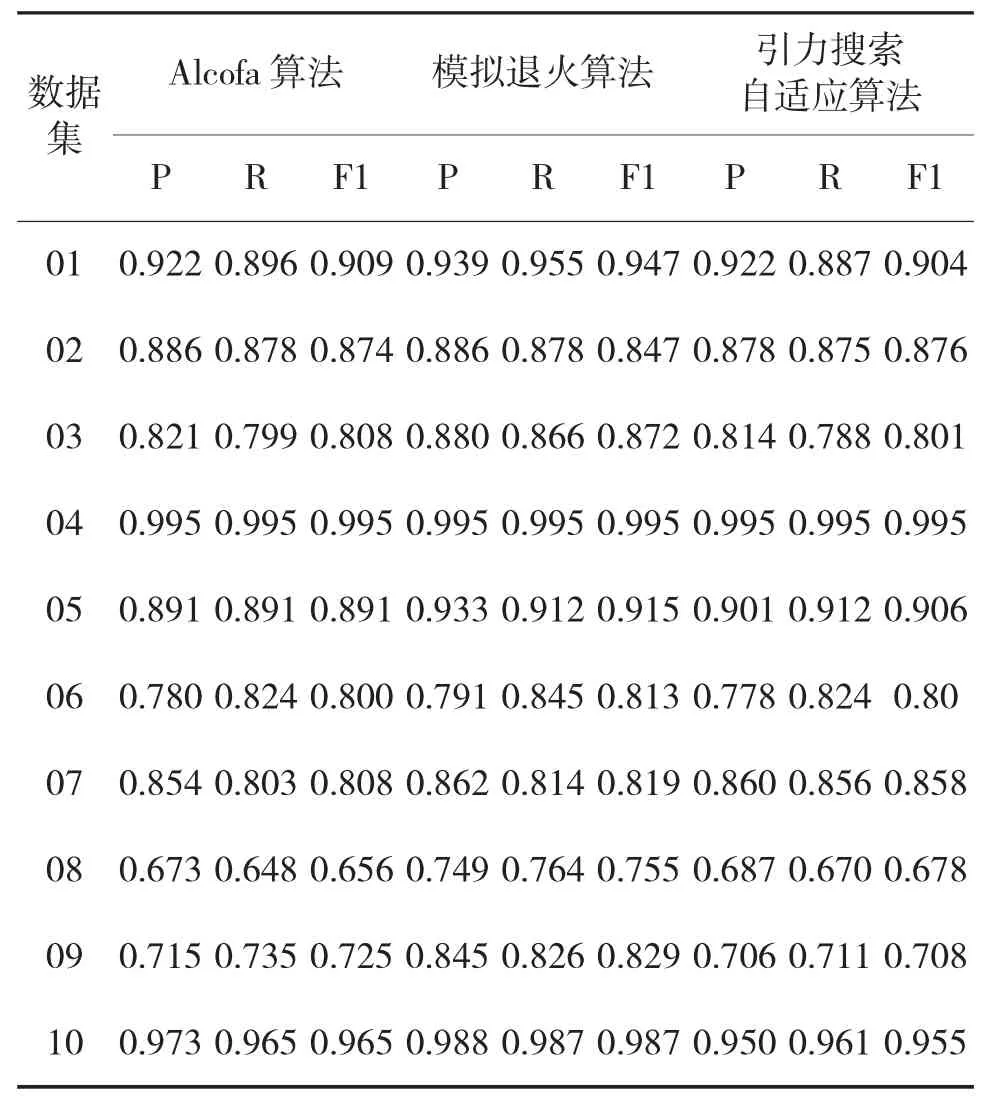
表4 3種算法所求閾值構建的分類器的性能比較

從表4的結果來看，對比10組數據庫的分類效果，在07、08號數據庫中引力搜索自適應算法略高于Alcofa自適應算法構建的分類器的分類能力，在04號數據庫，顯示兩者分類能力相同，其余7個數據庫顯示，Alcofa自適應算法構建的分類器的分類能力略高于引力搜索自適應算法所構建的分類器。對比上述十組數據顯示，模擬退火算法所構建的分類器的分類能力強于Alcofa自適應算法和引力搜索自適應算法。

出現引力搜索自適應算法的分類能力下降主要原因是，為了加快運行時間，對引力搜索空間進行了離散化的搜索限定，因此，在精度上有所下降，下面分別就引力搜索自適應算法對Alcofa自適應算法以及模擬退火算法的準確率（P）的平均誤差率μ1、μ2進行計算，來說明這種誤差是可接受的，以此說明該算法所得出的閾值有效。

由于平均誤差率μ1、μ2的值均小于千分之五，屬于可接受范圍之內，說明該算法所得出的閾值有效。

5 結論

為了消除或者抑制由不合理先驗知識帶來的模型噪聲，本文提出了一種基于規(guī)則提取的閾值自適應方法。本文以約簡結果中屬性的數量最小和相應決策規(guī)則的可信度最大為目標，結合引力搜索算法，并利用決策粗糙集中的閾值α，β為一特定離散取值時，不會改變等價類的劃分這一性質，對搜索空間離散化處理，然后給出基于智能算法的自適應求閾值算法。通過實例證明，本文提出的決策粗糙集閾值自適應方法是可行的。下一步需要努力在本文工作的基礎上考慮特定語義下的根據權重，構建新的目標函數將這一方法運用到更多方面。

參考文獻：

［1］YAO Y Y，WONG S K M，LINGRAS P.A decision-theoretic rough set model［C］//Raszw，Zemankovam，Proceedings of the 5th International Symposium on Methodologies for Intelligent Systems.North-Holland，1990：17-25.

［2］PAWLAK Z.Rough sets ［J］.International Journal of Computer and Information Sciences，1982，11（5）：341-356.

［3］PAWLAK Z.Rudiments of rough sets ［J］.Information Science，2007，177（1）：3-27.

［4］于洪，王國胤，姚一豫.決策粗糙集理論研究現狀與展望［J］.計算機學報，2015，38（8）：1628-1639.

［5］陳玉金，李續(xù)武，賈英杰，等.可變多重代價決策粗糙集模型［J］.計算機科學，2017，44（6）：245-249.

［6］MA X B，YANG X B，QI Y，et al.Multicost decision-theoretic rough sets based on maximal consistent blocks［C］//Miao Duoqian，Witold pedrycz.Rough sets and knowledge technology：9th International Conference.Shanghai：Springer，2014：824-833.

［7］DOU H L，YANG X B，SONG X N，et al.Decision-theoretic rough set：a multicost strategy ［J］.Knowledge-Based Systems，2016，91：71-83.

［8］LIANG D C，LIU D，WITOLD PEDRYCZ，et al.Triangular fuzzy decision-theoretic rough sets［J］.International Journal of Approximate Reasoning，2013，54：1087-1106.

［9］LIANG D C，LIU D.Systematic studies on three-way decisions with interval-valued decision-theoretic rough sets［J］.Information Sciences，2014，276：186-203.

［10］LIANG D C，LIU D.Deriving three-way decisions from intuitionistic fuzzy decision-theoretic rough sets［J］.Information Science，2015，300：28-48.

［11］LIANG D C，XU Z S，LIU D.Three-way decisions with intuitionistic fuzzy decision-theoretic rough sets based on pointoperators ［J］.Information Science，2017，375：183-201.

［12］HERBERT J P，YAO J T.Game-theoretical rough sets［J］.Fudanmenta Informaticae，2011，108（3）：267-286.

［13］JIA X Y，TANG Z M，LIAO W H，et al.On an optimization representation of decision-theoretic rough set model［J］.International Journal of Approximate Reasoning，2014，55：155-166.

［14］胡盼，秦亮曦，姚洪曼.用人工魚群算法自動確定三支決策閡值［J］.計算機與現代化，2016，32（6）：97-101.

［15］JIA X Y，ZHENG K，LI W W，et al.Three-way decisions solution to filter spam email：An empirical study［C］//Proceedings of the 8th International Conference on Rough Sets and Current Trends in Computing.Chengdu，China，2012：287-296.

［16］RASHEDI E，NEZAMABADI-POUR H，SARYAZDI S.GSA：A gravitational search algorithm［J］.Information Sciences，2009，179（13）：2232-2248.

［17］YAO Y Y，ZHAO Y.Attribute reduction in decision-theoretic rough set models［J］.Information Sciences，2008，178（17）：3356-3373.