城市軌道交通線路通過能力計算方法研究

魏玉光，夏　陽，賴藝歡

(1.北京交通大學 交通運輸學院，北京　100044；2.深圳市城市交通規劃設計研究中心 交通信息與交通工程重點研究室，廣東 深圳　518000)

引　言

城市軌道交通線路通過能力是指一定車輛類型、信號設備及行車組織條件下，單位時間內線路通過的最大列車數。合理的通過能力計算方法對于運營部門制定科學的運輸組織方案有著重要意義。

由于城市軌道交通在車站一般不設配線，列車在到達車站時需在正線上進行停站作業，且同一時間只允許一列列車進行停站作業，從而使得車站成為線路通過能力的重要限制因素。文獻[1]提出將車站和區間視為一個整體予以綜合分析，給定固定閉塞條件下列車追蹤間隔時間的計算公式，但本質上仍為車站追蹤間隔的計算方法。文獻[2]在引入移動閉塞概念的基礎上，比較移動閉塞和準移動閉塞的技術差異，提出城市軌道交通列車安全間隔時間計算方法，推導出移動閉塞和準移動閉塞列車安全間隔時間計算公式，對兩者進行仿真計算及分析。文獻[3]以追蹤間隔分析為基礎，對不同閉塞條件下城市軌道交通線路通過能力進行計算。文獻[4]提出一般情況下車站是限制通過能力的主要因素，且分別計算了在固定閉塞和移動閉塞條件下的車站間隔時間。文獻[5]通過計算機仿真方法對線路通過能力進行了深入研究。總結上述文獻，目前采用解析法計算線路通過能力時，需分別計算列車區間追蹤間隔和車站追蹤間隔。

此外，為滿足不同旅客出行需求，我國城市軌道交通組織快慢車模式的需求也在日益增長。但目前對于城市軌道交通快慢車模式下快車越行慢車以及通過能力計算的研究較少且多數為原則性研究。文獻[6]在分析越行點設置所受影響因素的基礎上，總結出越行點的設置原則。文獻[7]在傳統平行成對的運行圖基礎上，提出快慢車組合運營對系統能力損失的影響公式。

本文通過將列車停站作業虛擬化處理，提出一種新的城市軌道交通線路通過能力計算方法。新方法只需要計算列車區間追蹤間隔時間來確定線路通過能力。此外，本文利用此虛擬化處理的方法，研究快慢車模式下快車越行慢車的相關問題，建立快慢車模式下線路通過能力的計算模型。

1　列車停站作業虛擬化處理

為消除列車停站作業對于列車間隔計算的影響，本文將線路上除始發終到站外的各中間站分別虛擬為不同長度的閉塞分區，列車的停站作業轉換成列車在此長距離閉塞分區內不間斷運行的過程，即列車直接通過長距離閉塞分區，不再有制動、停站和啟動作業。本文將此長距離閉塞分區定義為虛擬閉塞分區。

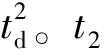
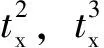
為保證列車運行全程總時間不變，將與虛擬閉塞分區相鄰區間的啟動時間差和制動時間差分別納入到虛擬閉塞分區運行時間中，則列車在虛擬閉塞分區內的運行時間為：

(1)

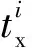
由于列車通過各虛擬閉塞分區時均以最大速度運行，因此在獲得列車在虛擬閉塞分區內的運行時間后，即可求得各虛擬閉塞分區的長度。

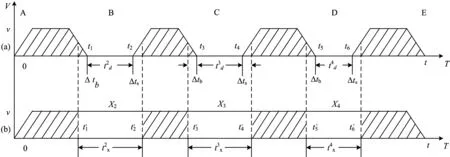
圖1　列車停站作業虛擬化處理

當線路上有n個車站時，則需建立除始發站和終點站外的n-2個虛擬閉塞分區。虛擬閉塞分區建立后，列車在全線路上進行不間斷追蹤運行，直至到達終點站。圖2中的(a)和(b)分別為虛擬閉塞分區建立前后的列車運行圖，BB′和CC′為B站和C站對應的虛擬閉塞分區。

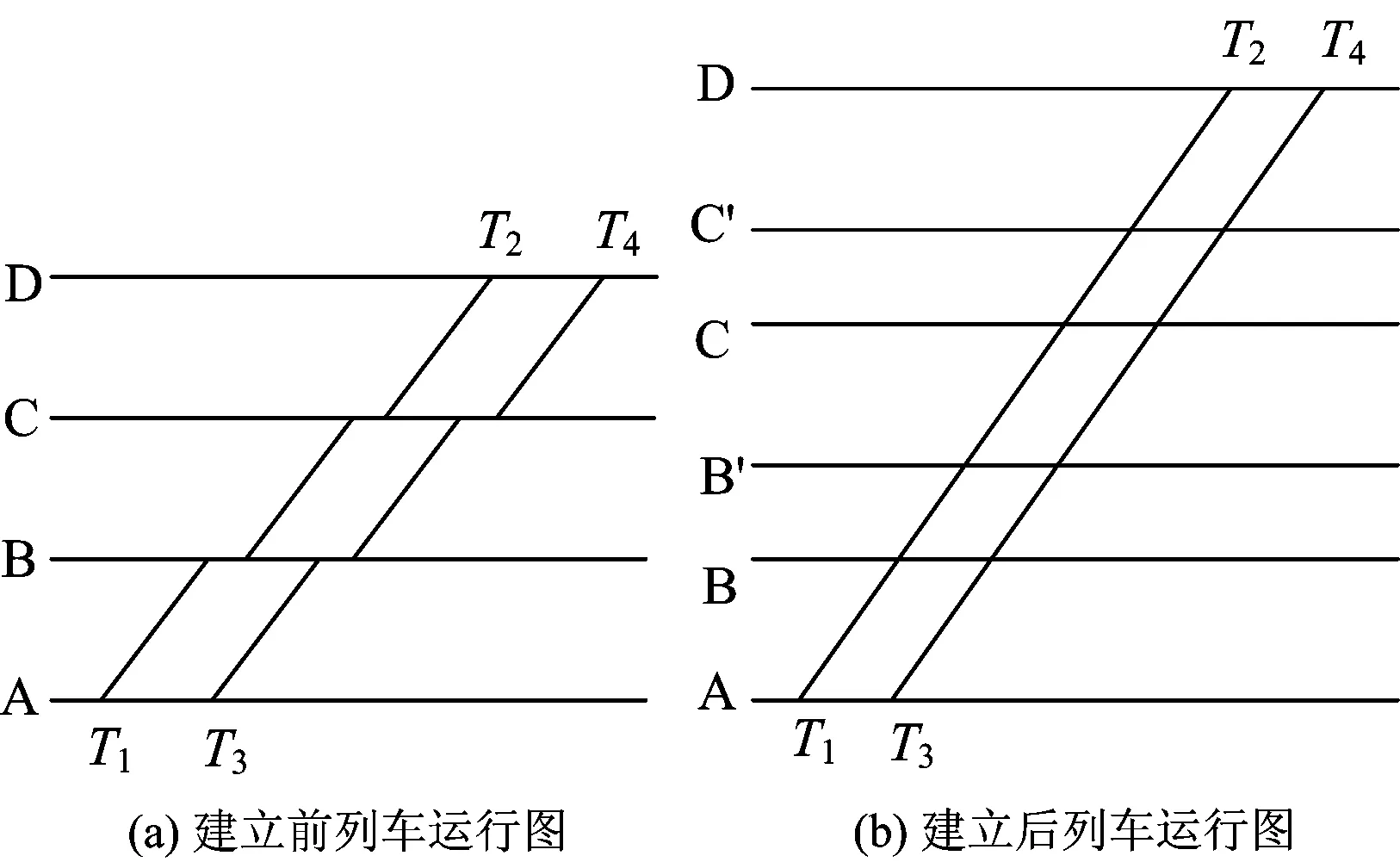
圖2　基于虛擬閉塞分區的列車運行圖

2　線路通過能力計算

2.1　固定閉塞條件下的列車追蹤間隔時間

虛擬閉塞分區建立后，線路上的閉塞分區包括既有的固定閉塞分區和新建立的虛擬閉塞分區，列車在全線路上進行不間斷追蹤運行。參考鐵路追蹤列車間隔時間的計算方法[8]，在使用三顯示自動閉塞的線路區段上，追蹤列車之間的間隔需相隔三個閉塞分區，如圖3所示。

在這種情況下，列車區間追蹤間隔時間為：

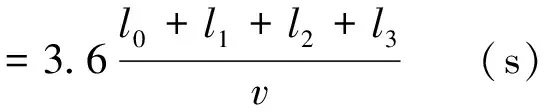
(2)

式中：l1，l2和l3為線路上固定閉塞分區或虛擬閉塞分區的長度，m；l0為列車長度，m；v為列車運行最大速度，km·h-1。

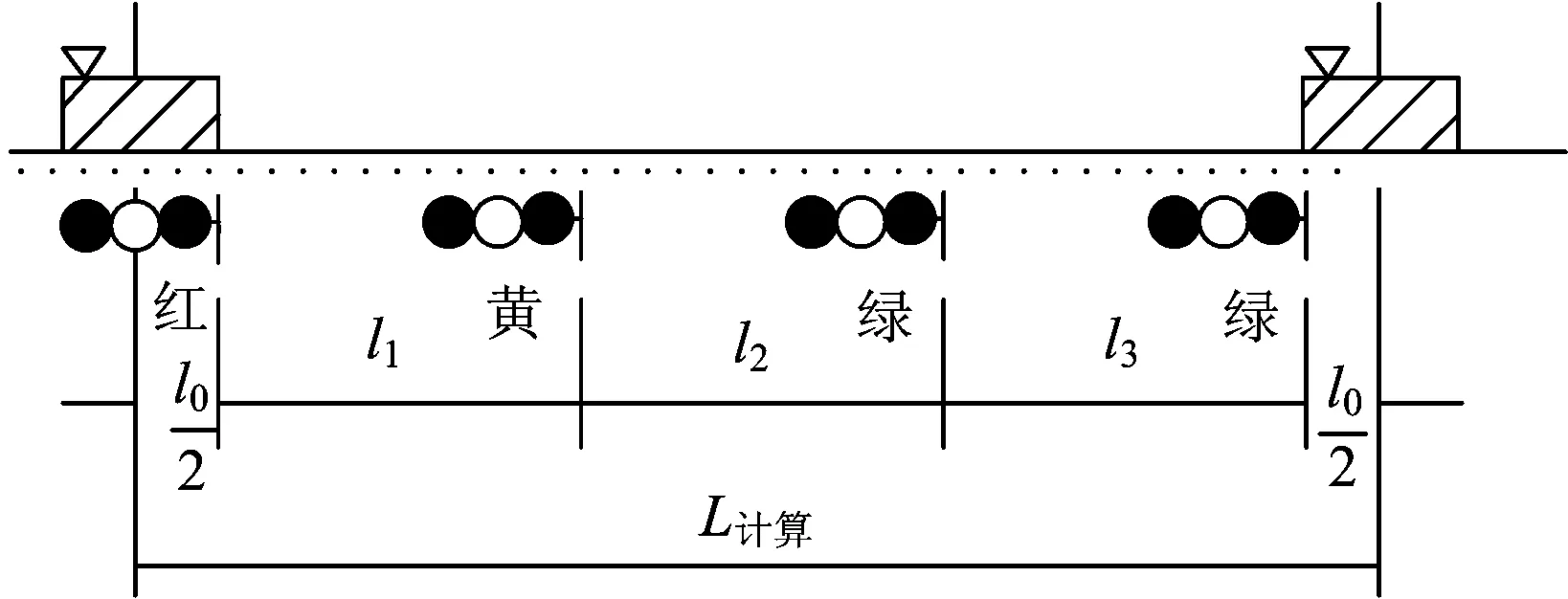
圖3　追蹤列車運行過程中的間隔距離

2.2　移動閉塞條件下的列車追蹤間隔時間

移動閉塞條件下，列車在區間進行追蹤運行時，后車制動目標點為前行列車尾部，并留有一定安全距離。考慮虛擬閉塞分區后，當前行列車駛入虛擬閉塞分區時，由于任何時刻只允許一列列車占用虛擬閉塞分區，因此后車制動目標點為前行列車所占用虛擬閉塞分區的起點再加上安全距離，類似于準移動閉塞的追蹤原理，如圖4所示。

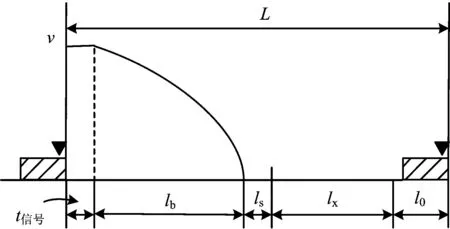
圖4　移動閉塞列車追蹤原理圖

因此，列車追蹤間隔時間為：

(3)

式中：t信號為列車動態信息傳輸時間，s；lb為列車制動距離，m；l0為列車長度，m；ls為安全防護距離，m；lx為限制虛擬閉塞分區的長度，m。

2.3　線路通過能力計算

在求得列車追蹤間隔時間后，需要將其與折返間隔時間進行比較，選取較大值作為列車間隔時間I，進而求得線路的小時通過能力為：

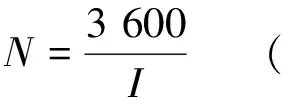
(4)

折返間隔時間的計算方法見文獻[4]，本文在此不做敘述。

與城市軌道交通線路通過能力現有計算方法相比，新方法仍需按照固定閉塞和移動閉塞條件分別計算線路通過能力。但新方法通過建立虛擬閉塞分區，使得不論在何種閉塞條件下都不需要考慮車站追蹤間隔，一定程度上簡化了計算思路。

此外，通過建立虛擬閉塞分區可以實現列車在停車站的運行圖“拉直”效果，對于研究快慢車模式下列車越行問題具有簡化作用。

3　快慢車模式系統能力分析

快慢車模式下，慢車為站站停列車，而快車僅在客流量大的車站設置停車站，如圖5所示，其中實心圈表示列車在該站停車。因此，快慢車在運行過程中平均速度不同，從而使得線路通過能力受到部分損失。本文基于虛擬閉塞分區，計算快慢車模式下線路的通過能力。

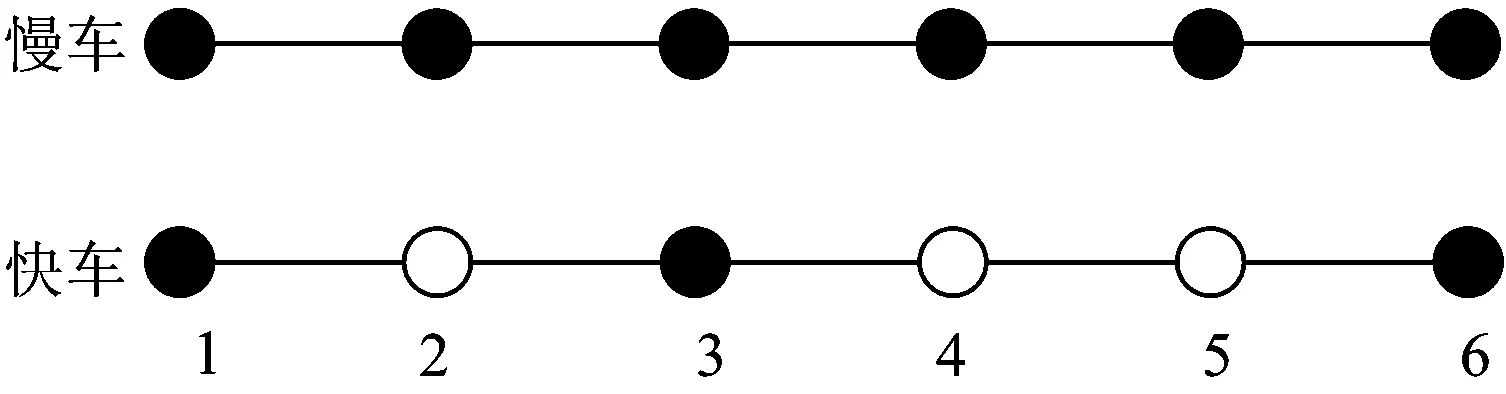
圖5　快慢車模式示意圖

設圖6為某條城市軌道交通線路，用N表示車站集合，n表示車站數量。該線各站從左至右依次編號為1，2，…，i，…，n。其中，車站1為起始站，車站n為終點站，用i對車站進行索引。為后文計算需要，設車站按終點站至始發站的順序進行排列時，車站編號為1，2，…，j，…，n，即編號1代表終點站，并用j對車站進行索引。

圖6線路示意圖

需要說明的是，在開行快慢車的城市軌道交通線路上，車站有多條配線，列車采用到達、到通、出發、發通間隔，此類間隔的組成與追蹤間隔不同，因此列車發車間隔I需按照傳統計算方法進行確定，計算方法參考文獻[9]。本文主要利用虛擬閉塞分區建立后對列車運行圖的改變研究快慢車模式下快慢車之間的越行問題，并在此基礎上分析系統通過能力。

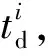
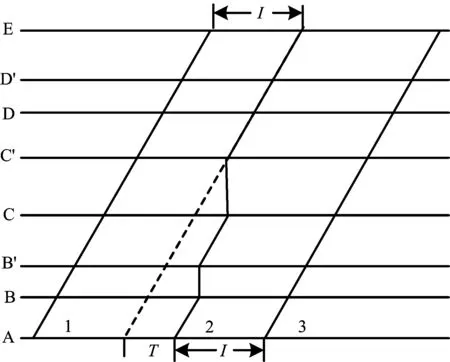
圖7　快慢車運行示意圖

在圖7中，快車在運行過程中不越行慢車，此方案下慢快車發車間隔增大為I+T，線路通過能力受影響較大。針對此問題，通常采取快車越行慢車的方法來提高線路通過能力。快車越行慢車應遵循以下原則：(1)快車不在其停車站進行越行；(2)快車在一個車站最多只能越行一列慢車，被越行慢車在該越行站所對應的虛擬閉塞分區內的運行時間被動延長為2I。圖8為3號快車越行2號慢車時的運行線變化示意圖。

因此，快慢車模式下的系統通過能力應按快慢車之間的具體越行情況進行分類討論。

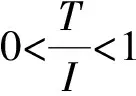
H=(p+1)I+T(s)

(5)

此時線路小時通過能力為

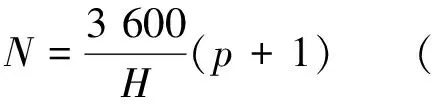
(6)

圖8　快車越行慢車運行圖

(2)為提高線路通過能力，將快車運行線向右平移I-T，使快車在第一個非停車中間站y1越行慢車，如圖9所示。

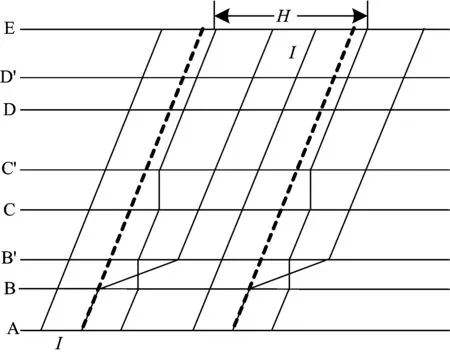
圖9　快車在首個非停車站中間站越行慢車

設1個周期內開行不被越行的慢車p列，則快慢車開行比例為1∶(1+p)，此時運行圖的周期為：

(7)

此時線路小時通過能力為：

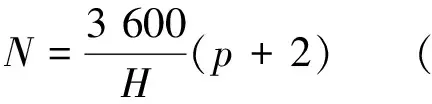
(8)

為計算線路通過能力，需確定各越行站的位置。具體步驟如下。

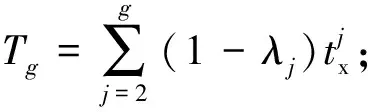
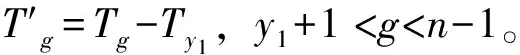
同樣設一個周期內開行不被越行的慢車p列，則快慢車開行比例為1∶(p+z)，則可計算得到運行圖周期為：

(9)

因此，線路小時通過能力為：

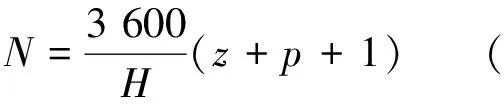
(10)

圖10　快慢車越行示意圖

4　案例分析

4.1　線路通過能力計算

北京市城市軌道交通5號線共設有23個車站，線路采用移動閉塞方式。相關技術參數見表1，上下行方向上各車站的停站時間見表2。

利用上述參數求得列車啟動時間差為12 s，制動時間差14 s，制動距離為268.8 m。另，上下行方向列車最大的停站時間均為50 s，可得列車在虛擬閉塞分區內最大的運行時間為76 s。將結果代入公式(3)中，得到列車追蹤間隔時間為102 s。而目前北京市城市軌道交通5號線采用站后折返的方式，折返出發間隔時間為99 s，因此以102 s作為列車間隔時間。將其代入公式(4)中，得到線路單向理論通過能力為35列·h-1。在目前的實際運營中，5號線早高峰列車運行間隔為2 min，單向通過能力為30列·h-1。

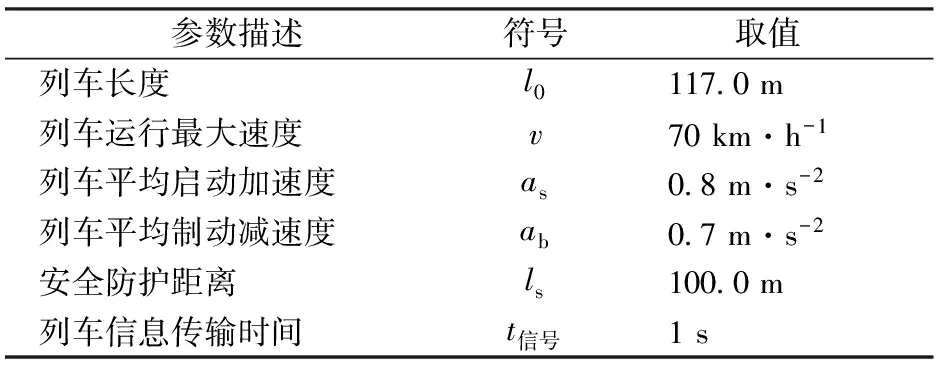
表1　技術參數

表2　上下行方向列車在各站的停站時間

4.2　快慢車模式下線路通過能力計算

現假設5號線將采取快慢車運輸組織模式(設滿足工程可行性)，同種列車間最小發車間隔為2分鐘。以上行方向為例進行計算，慢車在虛擬閉塞分區內的運行時間集合為Tx={0,71,71,56,71,76,76,56,71,56,56,76,56,56,76,58,76,56,56,76,61,64,0}。根據客流情況，設快車計劃在第3，6，7，12，15，17，20站停車，則快車行駛完全程較慢車節省時間T為844 s。因此，應按情形(3)確定越行站位置及系統通過能力。

設1個周期內開行不被越行的慢車1列，則快慢車開行比例為1∶7，則快慢車模式下運行圖周期H為967 s，系統通過能力29列·h-1，較目前線路通過能力僅損失1列·h-1。

5　結　論

本文通過將城市軌道列車停站作業虛擬化處理，提出了虛擬閉塞分區的概念，并基于此概念建立了城市軌道交通線路通過能力計算的新方法，研究了快慢車模式下越行站位置的確定方法。新計算方法屬于解析法范疇，在保持了計算思路完整性的同時，消除了既有方法需分別計算區間追蹤間隔和車站追蹤間隔的弊端，更為簡便。在計算開慢車模式下系統通過能力時，本文基于采用規格化列車運行圖的假設進行計算，計算結果表明可以實現在損失較小系統通過能力的前提下，開行適當列數的快車，以提高乘客旅行速度，滿足乘客不同出行的需求。

[1]張國寶. 地下鐵道通過能力計算方法的探討[J]. 上海鐵道學院學報, 1995, 16(1)：66-71.

(ZHANG Guobao. An Approach to the Computational Method of Subway Carrying Capacity [J]. Journal of Shanghai Institute of Railway Technology, 1995, 16(1): 66-71. in Chinese)

[2]羅麗云, 吳汶麒. 城市軌道交通移動閉塞列車安全間隔時間分析[J]. 中國鐵道科學, 2005, 26(1): 119-123.

(LUO Liyun, WU Wenqi. Analysis on the Safety Time Interval of Train with Movable Block System in Urban Rail Transit[J]. China Railway Science, 2005, 26(1): 119-123. in Chinese)

[3]路飛. 移動閉塞條件下地鐵列車的運行優化[D]. 山東: 山東大學, 2007.

(LU Fei. Operation Optimization of the Subway Train under Moving Block System[D]. Shandong: Shandong University,2007. in Chinese)

[4]毛保華. 城市軌道交通系統運營管理[M]. 北京: 人民交通出版, 2006.

(MAO Baohua. Operations and Management for Urban Rail Transit[M]. Beijing: China Communications Press, 2006. in Chinese)

[5]ABRIL M, BARBER F, INGOLOTTI L, et al. An Assessment of Railway Capacity[J]. Transportation Research Part E, 2008, 44(5): 744-806.

[6]湯玨, 陳富貴. 地鐵快慢車模式越行點的確定方法研究[J]. 鐵道工程學報, 2014, 193(10): 89-93.

(TANG Jue, CHEN Fugui. Determination Method of Overtaking Point in the Metro Express/Slow Train Mode[J]. Journal of Railway Engineering Society, 2014, 193(10): 89-93. in Chinese)

[7]湯玨, 陳富貴. 地鐵快慢車模式系統能力損失原則研究[J]. 鐵道工程學報, 2014, 195(12): 96-100.

(TANG Jue, CHEN Fugui. Research on the Principle of System Capacity Loss in the Mode of Express/Slow Urban Rail Transit[J]. Journal of Railway Engineering Society, 2014, 195(12): 96-100. in Chinese)

[8]楊浩. 鐵路運輸組織學[M]. 北京: 中國鐵道出版社, 2011.

(YANG Hao. Organization of Railway Transportation[M]. Beijing: China Railway Publishing House, 2011. in Chinese)

[9]張岳松, 田長海, 姜昕良, 等. 高速鐵路列車間隔時間的計算方法[J]. 中國鐵道科學, 2013, 34(5): 120-125.

(ZHANG Yuesong, TIAN Changhai, JIANG Xinliang, et al. Calculation Method for Train Headway of High Speed Railway[J]. China Railway Science, 2013, 34(5): 120-125. in Chinese)