對(duì)一道向量應(yīng)用題的研究
李國(guó)斌
(山西省長(zhǎng)治市第一中學(xué) 046000)
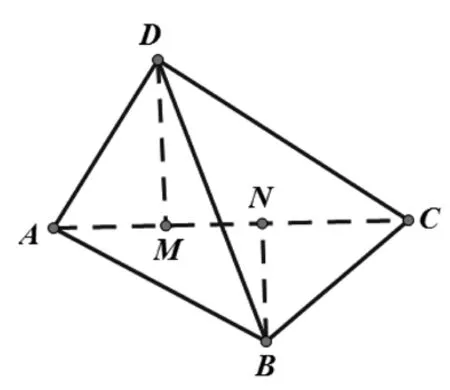
圖1
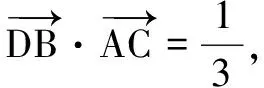
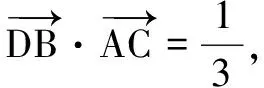
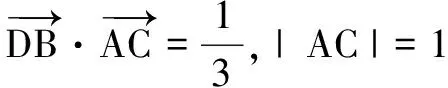
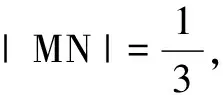
因?yàn)椤螦CD=θ,|AC|=1,所以DA=sinθ,DC=cosθ.
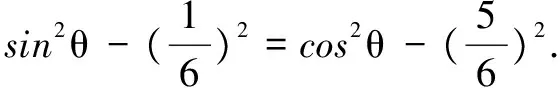
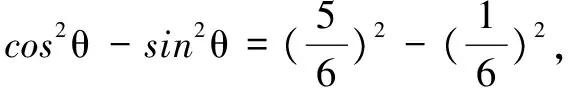
解析2 由條件AB=BC,想到利用模來轉(zhuǎn)化之.
解法2AD⊥DC,|AC|=1,在Rt△ADC中,DA=sinθ,DC=cosθ.
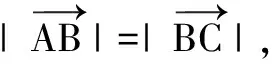

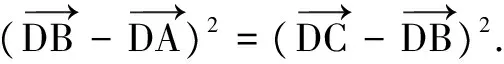
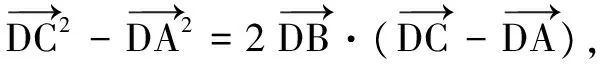
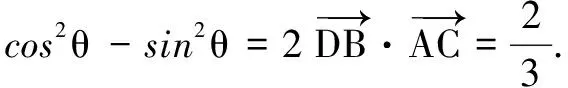
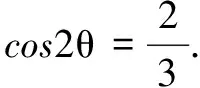
解析3 注意到AD⊥DC,|AC|=1,∠ACD=θ,可以想到容易解決點(diǎn)的坐標(biāo),所以想到坐標(biāo)法.
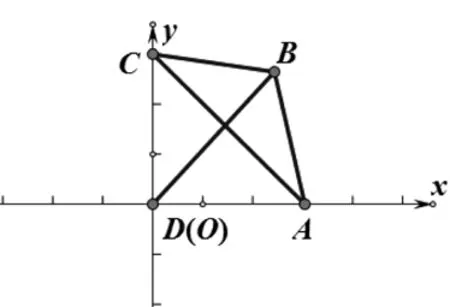
圖2
解法3 以D為原點(diǎn),DA所在直線為x軸,建立如圖2所示平面直角坐標(biāo)系.易得
D(0,0)A(sinθ,0),C(0,cosθ),設(shè)B點(diǎn)坐標(biāo)為(x,y),
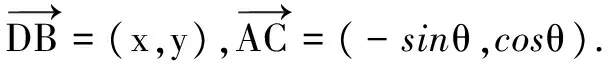
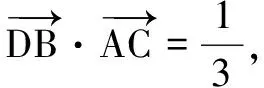
又因?yàn)锳B=BC,AB2=BC2,
即(x-sinθ)2+y2=x2+(y-cosθ)2.
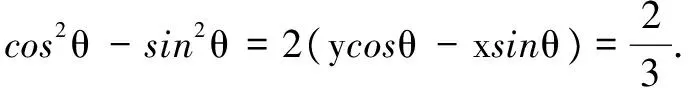
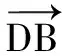
解法4 易得DA=sinθ,DC=cosθ,∠BAC=∠BCA.
由圖知:

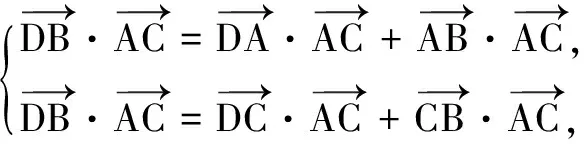
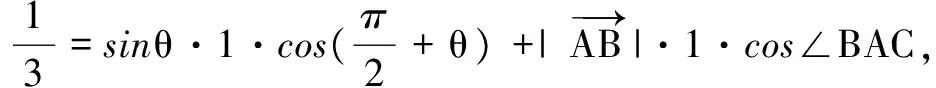
①
②
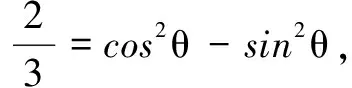
分析5 同上.

①
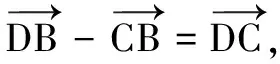
②
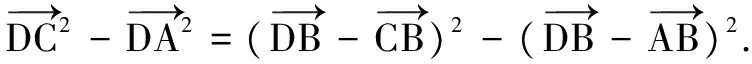
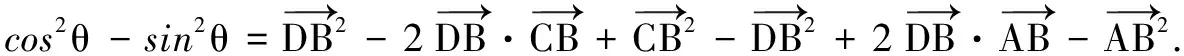
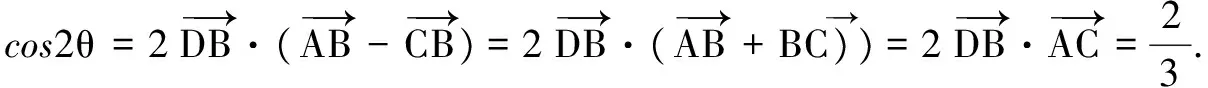
解析6 由平面幾何知識(shí)知,取AC中點(diǎn)O,連接BO,則
BO⊥AC,連DO,則∠DOA=2θ.直接利用∠DOA來求cos2θ,產(chǎn)生下列解法.
解法6 如圖3,取AC中點(diǎn)O,連BO,DO,作DH垂直AC于H.因?yàn)锳B=BC,所以BO⊥AC.又因?yàn)镈O是直角三角形ADC斜邊上的中線,所以DO=OC=0.5.所以∠DOA=2θ.
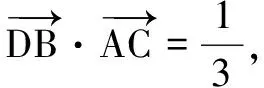
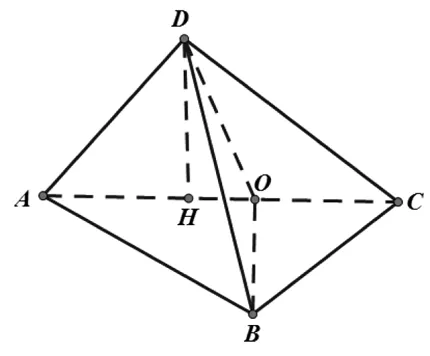
圖3
參考文獻(xiàn):
[1]吳選錄. 平面向量一道例題的拓展[J]. 中學(xué)數(shù)學(xué)研究,2017(7):16-18.
[2]王洪軍. 一道向量習(xí)題的推廣及應(yīng)用[J]. 中學(xué)數(shù)學(xué)研究,2017(2):23-24.

