基于經驗似然貝葉斯計算的穩定分布參數估計

錢 瑾，錢夕元

（1.攜程旅游網絡技術有限公司；2.華東理工大學 理學院，上海 200237）

0 引言

金融數據分布不僅僅呈現簡單的正態分布，大多具有“高峰厚尾”的特征，這是由于金融分布出現異常值的可能性更大，而單純刪除這些異常值是不科學的，會恰恰刪除了數據中可以反映金融風險的部分。穩定分布當參數α＜2時方差無限，可以擬合方差較大甚至無限的數據，恰好符合金融數據的“高峰厚尾”特征。穩定分布已經被證明對于金融數據具有良好的擬合性：1960年穩定帕累托分布被Mandelbrot[1]用于擬合金融市場收益率截尾數據，且被證明較正態分布可以更好地擬合波動價格分布。Mantegna和Stanley（1995）[2]提出，方差無限的穩定列維分布可以擬合紐約股票交易所S＆P500指數高頻數據的收益分布，且這些數據是尾部為近似指數下降的，并且位于中心（數據均值）6個方差范圍內。

穩定分布又被稱為列維穩定分布（Lévyalpha-stable distribution），它由列維于1920年提出，是一類沒有顯式密度函數表達式的連續概率分布。常見的一些分布如正態分布、柯西分布均是它的特例。廣義中心極限定理指出，若大量標準化后的獨立同分布隨機變量之和的極限分布存在，則為穩定分布族中的一種，即穩定分布是唯一吸引場的分布。穩定分布的這一特殊性使得它被應用在各類實證分析中。穩定分布的特征函數有4個參數，可以刻畫不同尾端厚薄、偏度、峰度特征的分布，具有較強的靈活性。但是穩定分布沒有顯式表達式，其分布參數估計存在一定困難。早期一些穩定分布參數估計方法包括：Du-Mouchel提出的極大似然法[3]、Nolan的直接積分法極大似然[4]、Zolotarev的特征變換法[5]以及McCulloch的分位數法[6]。可這些方法通常具有較大的局限性。顧娟和茆詩松[7]類似模擬矩法(SMM)的思想，提出并驗證了一種可以得到強相合結果的參數估計方法。武東和湯銀才[8]詳細介紹了穩定分布的一些性質，并證明了穩定分布在金融風險度量中應用的有效性。Peters[9]利用近似貝葉斯計算（Approximate Bayesian Computation，ABC）給出一元及多元穩定分布的參數估計方法。

本文采用基于經驗似然的貝葉斯計算（Bayesian Computation with empiricallikelihood，BCel）[10]對穩定分布進行參數估計：不僅通過模擬數據實驗驗證方法的有效性，還對2004年1月至2014年12月上證指數對數收益率數據對比正態分布進行實例研究，并利用穩定化的PP圖方法進行擬合優度的檢驗。同時，參考Pradhan[11]中基于Gibbs抽樣的貝葉斯預測的思路，本文提出基于經驗似然的貝葉斯預測，并利用該方法預測2015年1月至2016年8月上證指數收益率特征分布情況。

1 穩定分布及基于經驗似然的貝葉斯計算

穩定分布的定義分統計定義與參數定義兩種，穩定分布的參數定義是指穩定分布特征函數的參數表示，具體如下：

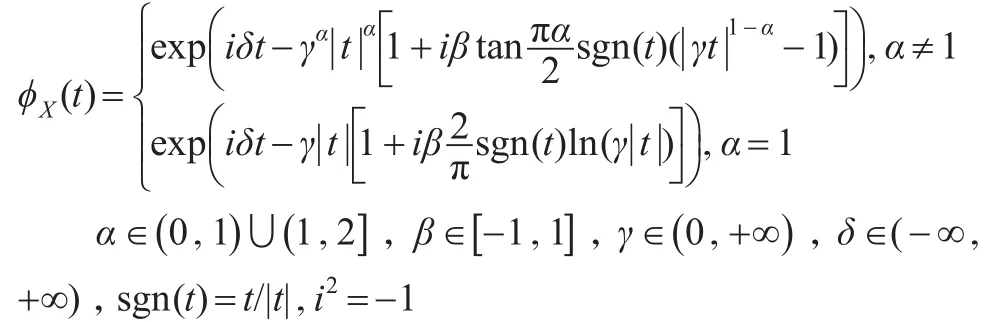
穩定分布一般需要四個參數α，β，γ，δ來描述。α是特征參數，也稱穩定化指數，是4個參數中最重要的參數，它可以刻畫尾端的厚薄程度，α越小峰越高，尾越厚。β為偏度參數，反映了分布的峰偏離分布均值的方向與程度，β＞0則分布右偏，β＞0則分布左偏。γ為刻度參數，而δ為位置參數。當α＞1時，穩定分布均值才存在，并且此時δ就是分布的均值。當α=2，β=0時穩定分布就是正態分布；當α=1，β=0時穩定分布則為柯西分布。若X～S(α，β，γ，δ)，則 [(X-δ)/γ]～S(α，β，1，0)。Chambers等[12]給出的基于S(α，β，0，0)穩定分布隨機數產生方法便是基于此種變換。

本文提出利用BCel對穩定分布進行參數估計的方法。BCel是基于經驗似然的一種貝葉斯計算方法，它的基礎是近似貝葉斯計算方法。Owen在1988年提出經驗似然，它是一類非參數似然，并且具有很多統計學的優勢。首先經驗似然構造置信區間有變換不變性、域保持性，而且置信域的形狀也是由數據決定。經驗似然的構建過程中，首先需要定義一個數據分布相關的功能函數θ：如分布的矩。具體來說，設獨立同分布）為服從f(x)的隨機變量，功能函數θ滿足限制條件EF[h(Y，θ)]=0 ，則經驗似然為p是集合中的值，而h的維數是θ的限制條件的個數。假設功能函數θ=Ef[Y]，在限制p1y1...pnyn=θ的條件下，經驗似然即為p1...pn的乘積的最大值。經驗似然已經被證明具有良好的收斂性，BCel是一種利用經驗似然改進近似貝葉斯計算得到的一種算法。具體的算法邏輯如下：

for i=1:M

（1）由先驗分布 π(·)抽樣，得到參數θi；

（2）由θ模擬抽樣得到對應功能函數；

i

（3）計算經驗似然Lel()，并作為權重wi賦給θi。BCel的計算結果是M個權重為wi的參數θi，g(θ)的估計值為當i的值越大，越接近于g(θ)的真實值。BCel方法可以在參數估計中充分考慮參數的先驗信息，而且計算較快較簡便。利用BCel對于穩定分布進行參數估計時，類似McCulloch[6]的利用抽樣的分位數來做估計的方法，本文將功能函數設為分位數，去對穩定分布進行參數估計。

2 基于經驗似然的貝葉斯預測方法

Pradhan[11]利用Gibbs抽樣與Monte Carlo模擬法對符合二參數的gamma分布的數據的未來觀測值進行了預測。借鑒Pradhan[11]的預測思路，本文提出一種基于經驗似然的貝葉斯預測方法。

設歷史數據y與未來觀測值y*，y*的后驗預測密度函數為：p(y*|y)= ∫p(y*|y，θ).p(θ|y)dθ，p(θ|y)在歷史數據y和先驗條件下的θ的后驗密度函數。因為y*，y獨立同分布，所以設（m為數據長度），則m個順序統計量為設次序統計量y*(r)（第r個）在已知數據y下的后驗密度為則對于穩定分布來說是對應穩定分布的概率密度，而很難解析表示，故結合Monte Carlo模擬利用抽樣得到的估計。

以上已經介紹過，以經驗似然為似然的后驗密度是p(θ|y)，而BCel的結果是M個有權重wi的參數θi，加權抽樣得到的參數θ值即為估計值。這一過程又叫做Monte Carlo模擬，同樣所 以的估計可以由以下抽樣過程獲得：

（1）利用參數先驗獲取參數 (θ1，θ2，...θn) ，并利用Chambers等[12]的穩定分布隨機數產生方法產生長度為m的n組隨機數

（2）計算n組隨機數的r個次序統計量

對于第r個順序統計量，其雙側100β%置信區間為下式，其中L代表上界，U代表下界：

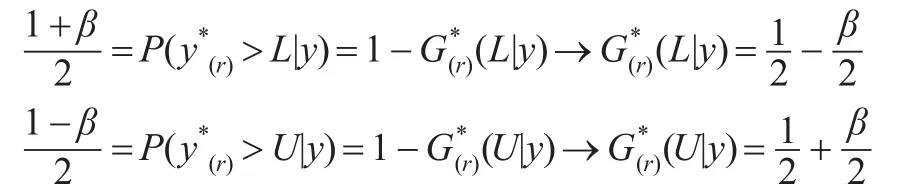
得到估計。

3 針對穩定分布的BCel參數估計及模擬實驗結果

因為α，β，γ，δ是嚴格限制定義域的，所以需要通過變換：ξ1=qnorm①qnorm:這里指R中stats包中函數，qnorm(x)代表取概率x在正態N(0,1)中對應的分位數；(α-1)②α的定義域為（1,2）；，ξ2=qnorm((β+1)/2)，ξ3=ln③ln(x)代表取底數為e的x的對數。將這4個參數轉變為定義域為(- ∞，+∞ ) 的1×4的參數矩陣ξ。因為希望利用Chambers等[12]給出的基于S(α，β，0，0)穩定分布隨機數產生方法產生穩定分布隨機數據，所以需要利用X～S(α，β，γ，δ)，則 [(X-δ)/γ]

下面討論利用BCel對穩定分布進行參數估計的具體方法及模擬實驗結果。～S(α，β，1，0)這一變換處理參數。而利用以上2種技巧就可以利用模擬產生需要的隨機數。

以上介紹過，X～S(α，β，γ，δ)，則 [(X-δ)/γ]～S(α，β，1，0)這一穩定分布的標準變換。又Famma（1971）年提出可以利用數據的分布特征直接得到參數γ，δ的估計值。所以利用BCel對于穩定分布進行參數估計的思路兩種，一是利用穩定分布標準變換得到S(α，β，1，0)，利用BCel估計參數α，β的值，而γ，δ的估計值Famma（1971）的方法得到；二是利用BCel直接估計穩定分布四個參數α，β，γ，δ的值。下面先介紹第一種思路的具體算法過程，假設原始數據集y服從穩定分布S(1.7，0.9，10，10)，且y的數據長度為200，利用標準化變換z=[(y-δ)/γ]可得z，即z～S(1.7，0.9，1，0)，對于變換后得到的數據集z計算累計概率密度為 0.1，0.2，...,0.9 的分位數qz1，qz2，...,qz9。設9×100的矩陣當功能函數θ′=(qz1，qz2，...qz9)時的經驗似然可以定義為：在限制p1Nz1...pnNzn=θ的條件下，p1...pn的乘積的最大值。由穩定分布標準變換與ξ1=qnorm①qnorm:這里指R中stats包中函數，qnorm(x)代表取概率x在正態N(0,1)中對應的分位數。(α-1)②這里α的定義域為(1 ，2] 。，ξ2=qnorm((β+1)/2)這一變換，知參數α，β，γ，δ(1.7,0.9,1,0)對應ξ(0.52，1.64，0，0)，取正態分布N(0，1)與N(1，1)作為參數ξ1與ξ2的先驗。利用以下步驟：

for i=1:10000：

（1）從先驗分布N(0，1)與N(1，1)中取，；

（2）由ξ1i，ξ2i利用變換得到αi，βi，再利用Chambers的隨機數產生方法，產生長度為200的隨機數mzi；

（3）計算9×100的矩陣Nmz為(t=1，..，9，j=1，..，200)；

（4）利用R包‘emplik’求出時對于Nmz的經驗似然Lel(θ′|mz)；

（5）對于參數αi，βi，設其權重wi=exp(log(Lel(θ′|z)))-

圖1的箱線圖在利用以上算法進行50次重復實驗后獲得。圖1箱線圖表示此方法的估計效果是良好的：α與真值很接近，而β的估計基本吻合參數真值，并且50組模擬實驗得到的參數α，β的估計值方差基本均小于0.1。若數據長度n=500，利用以上方法得到的α與β的估計值為1.72，0.78，具體的累計概率密度函數分布圖見圖2，可以看出此時擬合分布與真實分布更為接近。

圖1 50次重復實驗得到的穩定分布參數估計結果

圖2 n=500時的累計概率密度分布擬合圖

下面討論不利用穩定分布標準化變換，直接對穩定分布利用BCel進行參數估計的方法。依上取穩定分布S(1.7，0.9，10，10)，原始數據集y長度為200，對于穩定分布直接利用BCel進行參數估計不同與之前的算法過程的幾點主要在于：

（1）不需要將y標準化轉為z，進而求z的分位數的值。而是直接求y的概率為0.1，0.2，...0.9的分位數qy1，qy2，...qy9，并在計算經驗似然的過程中將其作為功能函數θ′；

（2）通過變換ξ1=qnorm(α-1)，ξ2=qnorm((β+1)/2)，ξ3=ln③ln(x)代表取底數為e的x的對數。(γ)，ξ4=δ，將參數α，β，γ，δ(1.7，0.9，10，10)轉化為對應的ξ=(0.52，1.64，2.30，10)，并且對于 4個參數2，ξ3，ξ4分別取N(0，1)，N(1，1)，N(0，2)及N(0，10)作為先驗。

除此之外過程大體與只估計2參數的相似，表1表示各個不同的方法得到的四參數穩定分布的參數估計值，其中第一列至第四列分別表示Buckle（1995）[13]利用Gibbs抽樣，McCulloch（1986）[6]利用分位數法，Lombardi（2007）[14]利用反向MCMC法，本文利用BCel法，在10次重復實驗的基礎上得到的結果。

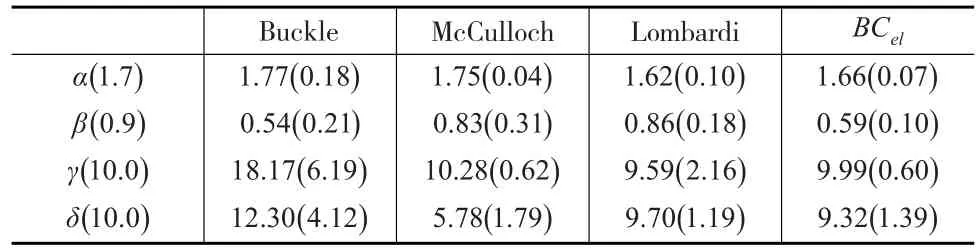
表1 四參數穩定分布的估計結果

表1數據表明：相較與其他三種方法，BCel對于參數α，γ，δ的估計較為精準，尤其對于參數α，δ，方法BCel的估計精度是最高的。可是BCel對于參數β的估計有些偏差，只能做到與其他方法持平。但總體來說BCel的估計結果的總體標準差更小，估計效果更加穩定。

4 實證

本文對于2004年1月2日至2014年12月31日的上證綜合指數日收盤價數據（共2640個）利用BCel方法進行了分析。假設時間序列{Pt}對應這2640個數據，應用對數收益率變換：yt=100·(lnPt-lnPt-1)，可得序列{yt}。{yt}的均值為0.029，方差為2.923，序列的偏度與峰度為0.877與22.376，滿足上文闡述的金融數據的“高峰厚尾”的特征。利用上文說明的2種BCel估計方法對于序列進行分布擬合。首先說明第一種方法的應用過程：采用數據均值，Famma（1971）的估計方法得到參數γ，δ的估計，利用BCel估計參數α，β，且這一過程中采用的先驗分布，模擬次數均與之前的模擬實驗相同。這一方法得到的參數估計值為(1.88,0.12,0.84,0.029)。而采用直接利用BCel估計4個參數的方法得到的參數估計結果為(1.56,0.122,0.837,-0.12)。同時，采用正態分布對比進行擬合，得到的正態分布為N(0 .029，2.913) 。

PP圖是檢驗分布擬合數據優度的一種重要的方法，可是傳統的PP圖存在很多問題：采用的均勻分布的次序統計量方差不穩定，且波動較大；曲線尾部無法準確反映對數據的擬合優度等。Michael針對PP圖的此類缺陷提出了穩定化的PP圖，穩定化的PP圖采用均勻分布U經變換后得到的分布的次序統計量，這些次序統計量的漸進方差相同，且上下波動較小，故穩定化的PP圖可以更好地進行擬合優度的檢驗。圖3是利用穩定化的PP圖對于上段得到的估計結果：穩定分布S(1.88，0.12，0.84，0.029)（標準化后穩定分布BCel擬合結果），S(1.56，0.122，0.837，-0.12)（四參數穩定分布BCel擬合結果），正態分布N(0 .029，2.913)進行擬合優度檢驗后的結果。圖3表明正態分布的擬合優度遠不及其他2類分布。而穩定分布標準化后的估計結果S(1.88，0.12，0.84，0.029)較穩定分布直接估計的結果S(1.56，0.122，0.837，-0.12)對于數據的擬合優度更好。

圖3 PP圖對于3類分布擬合檢驗結果

為了進一步進行數據分布擬合檢驗，圖4繪制了數據的頻率直方圖及估計得到的正態分布N(0 .029，2.913) ，穩定分布S(1.88，0.12，0.84，0.029)的密度函數圖。圖 4表明穩定分布S(1.88，0.12，0.84，0.029)對于數據的擬合程度與數據特征的表現程度遠遠優于正態分布，這不僅說明了穩定分布可以更好地擬合金融數據“高峰厚尾”的特征，也說明BCel方法可以較好地估計穩定分布參數的值。基于穩定分布S(1.88，0.12，0.84，0.029)對數據的較優的擬合性，可以得到數據本身的一些特征：得到的穩定分布參數α估計值小于2說明上證指數對數收益率存在相關性，并不滿足隨機游走；而得到的參數估計值β大于0說明上證指數對數收益率呈現右偏的厚尾分布。

圖4 上證指數收益率的頻率直方圖及正態分布、穩定分布密度函數圖

由于時間序列數據受周期性的時間因素影響較大，為了對2015年1月至2016年8月的上證指數對數收益率進行預測，歷史數據選取2012年1月至2014年8月的上證指數對數收益率數據。利用前文給出的基于經驗似然的貝葉斯預測方法與4參數的穩定分布的BCel方法，利用歷史數據預測了未來數據的一些特征的分布情況。圖5是預測的未來數據的最小值、中位數、最大值的概率密度圖，預測的最小值、中位數、最大值的95%的置信區間為(-46.01，-6.482 )，(- 0.53，0.51) ，(6 .31，46.74 )。而 2015中位數、最大值的真值(- 8.87，0.15，5.60 )用虛線標出，可以看出最小值與中位數的真值落在預測的最小值，中位數的95%的置信區間內，預測結果較好。而最大值真值略小于預測的區間的最小值，應該是因為2012年1月至2014年8月的數據的“高峰”特征更明顯，所以預測結果存在偏差。年1月至2016年8月的上證指數對數收益率的最小值、

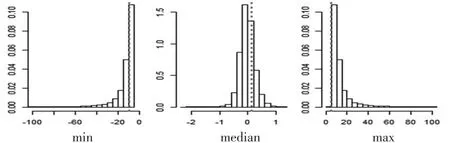
圖5 預測數據的最小值、中位數、最大值的概率密度圖

5 結論

本文介紹了基于經驗似然的貝葉斯計算方法，并利用該方法對穩定分布進行參數估計并且得到良好的模擬實驗參數估計效果。同時本文借鑒Pradhan的基于Gibbs抽樣的貝葉斯預測方法的思路，提出一種基于經驗似然的貝葉斯預測方法，并從理論層面解釋了該方法。在上證指數對數收益率的實證研究中，先是利用BCel方法結合穩定分布擬合數據，其擬合結果不僅證實了穩定分布較正態分布更適合擬合“高峰厚尾”特征的數據，也證實參數估計方法的準確性；之后又通過歷史數據預測未來數據的特征情況，得到了符合預期的結果。

參考文獻：

[1]Mandelbrot B.The Pareto-Levey Law and the Distribution of Income[J].International Economic Review,1960，（1）.

[2]Mantega R M,Stanley H E.Scaling Behaviour in the Dynamics of an Economic Index[J].Nature,1995，（367）.

[3]DuMouchel W.Stable Distributions in Statistical Inference:Informa?tion from Stably Distributed Samples[J].Journal of the American Sta?tistical Association,1975，（70）.

[4]Nolan J P.Numerical Computation of Stable Densities and Distribu?tions[J].Comm.Stat.Stochastic Models,1997，（13）.

[5]Zolotarev V M.One-dimensional Stable Distributions[J].Translations of Mathematical Monographs,1986，（65）.

[6]McCulloch J H.Simple Consistent Estimators of Stable Distribution Parameters[J].Comm.Stat.Simulation and Computation,1986，（15）.

[7]顧娟,茆詩松.穩定分布的參數估計[J].應用概率統計,2002，（18）.

[8]武東，湯銀才.穩定分布及其在金融中的應用[J].應用概率統計,2007，（23）.

[9]Peters G W,Sisson S A,FanY.Likelihood-free Bayesian Inference Forα-Stable Models[J].Computational Statistics and Data Analysis,2012，（56）.

[10]Mengersen K L,Pudlo P,Robert C P.Bayesian Computation via Em?pirical Likelihood[J].Proceedings of the National Academy of Sci?ences,2012，（110）.

[11]Pradhan B,Kundu D.Bayes Estimation and Prediction of the two-parameter Gamma Distribution[J].Journal of Statistical Com?putation and Simulation,2011，（81）.

[12]Chambers J,Mallows C,Stuck B A.Method for Simulating Stable Random Variables[J].Journal Am.Statist.Assoc.,1976，（71）.

[13]Buckle D J.Bayesian Inference for Stable Distributions[J].Journal of the American Statistical Association,1995，（90）.

[14]Lombardi M J.Bayesian Inference for Alpha Stable Distributions:A Random Walk MCMC Approach[J].Computational Statistics&Da?ta Analysis,2007，（51）.