某電站大壩參數反演分析

王新棟,漆文邦,張江潮

(四川大學,成都 610065)

0 前 言

隨著大壩觀測技術發展的深入、大壩測量設備精度的提高、大壩監測理論的逐漸成熟，在大壩監測原始觀測數據的基礎上，利用反演分析來推測壩體混凝土及基巖材料參數的方法業已成熟。反演分析法的原理基于現場測量的位移、應力、應變等數據，通過反演模型推出一些參數(比如彈模、泊松比等)的方法[1]。其最終結果是基于大壩實測數據，建立理論預測模型擬合大壩的各種特征，以此來反饋控制大壩的安全。

位移量是描述物體受力變形形態的一類重要物理量，目前已被用作反演分析確定巖土工程材料特性參數的主要依據[2-3]。

1 工程概況

某水電站是一座以發電為單一目標、具有日調節水庫的高水頭引水式電站。電站總裝機52 MW，設計水頭233.00 m，最大水頭272.00 m，最小水頭233.00 m，加權平均水頭258.00 m，最大引用流量24 m3/s，保證出力11.57 MW，年利用小時數5 110 h，年發電量2.45億kWh。電站水庫正常蓄水位1 090.00 m，設計洪水位1 084.60 m，校核洪水位1 088.85 m，電站正常蓄水位以下庫容26萬m3，調節庫容21.2萬m3，水庫具有日調節能力。本工程屬Ⅳ等工程，永久建筑物按4級次要建筑物按5級設計。相應防洪標準，首部樞紐永久性建筑物按50年一遇洪水設計、200年一遇洪水校核。

某水電站首部建有一座有長126.6 m、最大閘高31 m的攔河閘壩日調節水庫。首部樞紐從左至右依次布置有左岸錨索邊坡、進水閘、泄洪閘(1、2、3號閘)、表孔閘(4號閘)、右岸擋水壩段及右岸護岸工程。進水閘側向布置在左岸，其軸線與攔河閘壩軸線夾角為50°。閘室前為設有靜水柵的靜水段和沉礫段，此段與隧洞進水口之間設高程為1 077.50 m的攔沙砍。隧洞進水閘前設有攔污柵，攔污柵底板下布置3孔沖沙孔，孔底高程1 074.00 m，3孔沖沙孔匯集于后面的1.0 m×1.5 m(寬×高)沖砂廊道。3孔泄洪沖砂閘(1、2、3號閘)緊靠進水閘右側布置，為平底板閘，孔口尺寸7.0 m×8.0 m，每孔設弧形工作閘門各1道，共用1道平板檢修門。閘底板高程1 070.50 m，閘頂高程1 091.50 m，閘室長39 m，墩厚分別為2.60 m(邊墩，與進水閘分縫)、3.6 m、3.2 m(2號與3號閘墩，中間縫寬2 cm)、3.2 m(3號閘與表孔閘中間縫寬2 cm)。1、2、3號閘基礎建基面1 060.50 m。表孔閘(4號閘)緊靠3孔泄洪沖砂閘布置，閘孔寬7.0 m，閘室長39 m。堰頂采用WES曲線，堰頂高程1 083.00 m，溢流面采用400號硅粉混凝土防沖，4號閘基礎建基面1 060.50 m。

2 反演分析方法

水利及巖土工程的反演分析可以分為以下幾類：位移反分析法、應力反分析法以及二者結合綜合反分析法。位移反分析法是目前應用最為普遍的方法，它又分為解析法及數值法。解析法更多的適用于求解較為簡單邊界條件下的線粘彈性問題，在解決這類問題時解析法優點突出，主要表現在概念明確、計算速度快。相比之下，數值法解決范圍更加廣泛，且主要用在解決復雜邊界及復雜地質條件下的非線性問題。根據數值法的求解過程不同，可以分為正反分析法、逆反分析法等[4-5]。

正反分析法指的是首先指定待反演參數的初始值，通過大型計算軟件進行正分析得到典型測點的變位或者應力，之后將計算值與實測值進行擬合比較，當誤差較大時通過有效方式調整待反演參數，再重復以上操作直至計算值與實測值之間的誤差達到允許的范圍內，此時取定的待反演參數值即作為反演計算的最終結果。正反分析方法程序編制簡單，計算方法靈活、適用非線性問題的參數反演[6-7]。

逆反分析法與正反分析法的計算程序相反，它是指根據待反演參數與實測值之間的某種關系，直接求解出由該關系式組成的方程組，即可得到反演參數。該方法原理簡單直觀，且步驟簡單，計算用時短，但是需要進行程序編制，且更多情況下適用于線性問題的反演[8]。

考慮到某水電站大壩已進入運行期，經模型有效性初步驗證，多元線性回歸及逐步回歸效果良好，因此本文采用基于多重響應面的位移正反分析法來進行材料參數的反演分析。

基于響應面方法的原理，提出多重響應面方法來擬合壩體參數與大壩在荷載作用下產生的順河向位移之間的非線性映射關系，相比于其他反分析方法存在的大量的數值計算過程，該方法可以有效減少數值計算次數，節省反分析時間，提高計算效率。

為了保證計算效率和準確度，在本文中，運用不帶交叉項的 2 次響應面函數，其表達式為：

(1)

式中：x=(x1,x2,…,xn)為待反分析矢量；a、bi、ci(i=1,2,…,n)為待定系數。式(1)中右端共有2n+1個待定系數，需要有2n+1個方程才能求解。在本文的反分析中s(x)代表位移，x代表待反演參數。

采用響應面法對大壩的各個參數進行反分析，將計算軟件內部的計算過程用響應面方程來近似，可大大減少軟件的計算次數，提高反分析效率。

3 有限元模型

3.1 變形監測

2013年9月，根據電站監測設施施工設計圖及電站現場實際情況，在右岸布置二等單三角控制網，其中BL1、BL3作為日常水平位移監測的工作基點，BL2作為檢查點。高程控制點，需由原監測點聯測至BL2和BL3，BL2作為垂直位移監測的工作基點，BL3作為檢查點。垂直位移監測均采用二等水準進行測量。

垂直位移點和水平位移點均布設在同一位置，參照原設計的點位布設，右岸擋水壩測點編號：LD1，壩頂上游側測點編號：LD2、LD3，進水口的閘墩測點編號：LD4，下游閘墩測點編號：LD5、LD6。首部樞紐變形監測點布置見圖1。

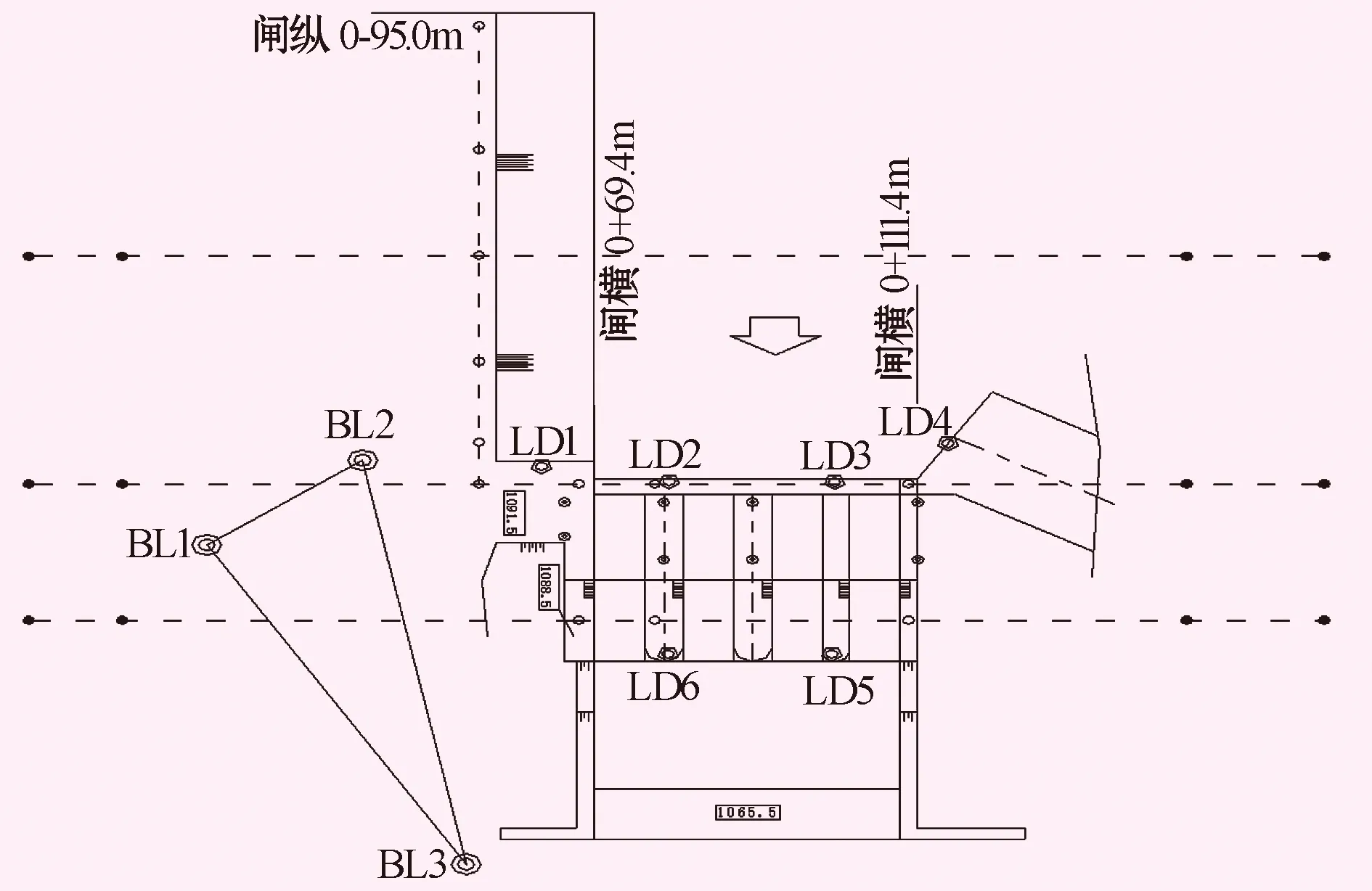
圖1 首部樞紐變形監測點布置圖

3.2 有限元模型的建立

電站首部樞紐從左至右依次布置有左岸錨索邊坡、進水閘(側向布置在左岸)、泄洪閘(1、2、3號閘)、表孔閘(4號閘)、右岸擋水壩段及右岸護岸工程。本文采用基于多重響應面的位移正反分析法來對電站大壩泄洪閘段某些參數進行反演，分析軟件采用大型通用有限元軟件ANSYS來進行分析。并將反演得到的參數進行正分析運算，通過應力及變形結果來驗證反演參數的合理性。

模型采用D-P準則，壩體與基礎網格采用八節點六面體SOLID45單元。

模型采用計算坐標系如下：

X軸,順河流方向，指向下游為正方向。

Y軸,鉛垂方向，鉛垂向上為正方向。

Z軸,垂直于水流方向，指向右岸為正方向。

模型范圍：

(1) 泄洪閘。泄洪閘壩段由3個閘室組成，其中靠近右岸的2個閘室連為一體，與靠近左岸的閘室用沉降縫分離。泄洪閘三維計算模型僅選取連為一體的2個閘室，閘高31 m。模型邊界確定為鉛垂方向取至閘室底邊界以下62 m；順河向上游取至閘室上游邊界以上50 m，向下游取至閘室下游邊界以下50 m；垂直水流方向以閘室左右邊界起向左右各延伸50 m。模型共劃分51 582個單元，56 210個節點。

(2) 表孔閘。表孔閘閘高31 m。模型邊界確定為：鉛垂方向取至閘室底邊界以下62 m；順河向上游取至閘室上游邊界以上50 m，向下游取至閘室下游邊界以下50 m；垂直水流方向以閘室左右邊界起向左右各延伸50 m。模型共劃分36 156個單元，39 710個節點。

模型邊界基礎四周和底面采用法向約束，結構頂部及四周采用自由邊界。

4 參數反演分析計算

電站泄洪閘壩段及地基共7種材料，每種材料有5個參數，如果全部反演，則工程量十分浩大。從大壩建成到現在已經運行了17 a，隨著時間的推移，混凝土的彈性模量也在逐步的變化，因此本文針對影響大壩變形的6個主要參數進行反演分析，依次是基巖t1彈模、基巖t2彈模、基巖t1泊松比、基巖t2泊松比、C10彈模、C20彈模。反演過程中通過2個工況的位移計算值差值與實測差值的擬合度來判定反演參數是否合理。

溫度因子是影響混凝土大壩變形的最主要因素，為了盡量減小誤差及消除溫度場對位移造成的影響，本文選取溫差最小、上游水位差值最大且受時效因素影響最小的2015年1月24日(溫度6 ℃，上游水位1 084.00 m，下游水位1 065.60 m，定義為工況1)、2015年2月25日(溫度6.5 ℃，上游水位1 088.51 m，下游水位1 065.60 m，定義為工況2)2種工況下的實測數據來進行參數的反演。反演過程中通過工況2與工況1的位移計算值差值y2′-y1′與實測差值y2-y1的擬合度來判定反演參數是否合理。根據電站水庫運行方式可知：首部樞紐泄洪沖沙閘及表孔溢流壩在枯期(12月-翌年3月)均關閉，可保持水位在1 090.00 m運行。若遇水位超過1 090.00 m時可開啟表孔閘門進行調節，以保證水庫運行水位在1 081.50～1 090.00 m內運行。而2種工況下的水位上游水位均小于1 090.00 m 。綜上可知2種工況下閘門全部關閉。以此來作為荷載施加的依據。

(1) 計算中選用不帶交叉項的二次多項式作為響應面函數，共有6 個變量，所以響應面函數有 13個未知量。根據土工試驗及地質報告得到的各個物理力學參數的建議值，通過SPSS軟件進行正交試驗得到13組參數組[9]。

(2) 分別取由第(1)步得到的13 組參數組里面的每一組參數，用ANSYS軟件做 13次正分析計算，得到13組泄洪閘壩段的LD2、LD3、LD5、LD6測點順河向及垂直位移數據。

(3) 對于LD2監測點，將第一組參數值與位移值代入式(1)得到含有13個未知量的一次方程。以此類推，由另外 12 組參數值及位移值可以得到相應的12個方程，總共可以得到由13個線性方程組成的方程組。經求解得到在LD2測點處建立的響應面函數系數。同樣的，對LD3、LD5、LD6監測點，采用同樣的方法，得到其對應的響應面函數的二項式系數。

將響應面函數的系數值帶入式(1)，可得LD2測點的響應面函數。同樣方法可得到LD3、LD5、LD6測點的響應面函數。

(4) 建立8個響應面函數方程后，需要找到 1 組參數值，使得由這8個響應面得到的2種工況下的計算位移差值與實測差值之間的差值的平方和最小，即使得目標函數最小。本文采取matlab中的優化工具箱來進行多參數的優化求解，得到的6個待反演參數值如表1所示。

η= [S2H(x)-(0.39)]2+[S2V(x)-(0.2)]2+

[S3H(x)-(1.33)]2+[S3V(x)-(0.1)]2+

[S5H(x)-(0.27)]2+[S5V(x)-(0.4)]2+

[S6H(x)-(0.32)]2+[S6V(x)-(0.2)]2

(2)

表1 反演參數數據表

將6個反演參數值在2種工況下通過ANSYS軟件進行正分析，得到LD2、LD3、LD5、LD6測點的順河向及垂直位移數據計算值的差值與實測值位移數據差值，如表2所示。

可以看出：4個測點中LD2、LD5、LD6的順河向位移計算差值與實測位移差值都比較接近，只有LD3相差較大。4個測點中LD5、LD6垂直位移計算差值與實測位移差值較接近，LD2、LD3的垂直位移計算差值的符號為負，而實測垂直位移差值符號為正。規定向下沉降為正，向上抬升為負。壩體受到指向下游的推力大于指向上游的推力；同時壩體自身結構分布均勻，底板所受的揚壓力從上游往下游逐漸減小。兩者共同作用導致壩體所受順時針方向彎矩。而工況2的上游水位比工況1高4.5 m左右，2種工況的下游水位相等，工況2大壩產生的向順時針方向的彎矩作用更大，因此工況2位于閘墩上游側的LD2、LD3測點垂直位移較工況1小，位于閘墩下游側的LD5、LD6測點垂直位移較工況1大，LD2、LD3垂直位移2種工況下計算值的差值為負，LD5、LD6垂直位移2種工況況下計算值的差值為正是合理的。綜上可知，小部分實測數據在觀測過程中可能存在一定的誤差，大部分實測數據差值與位移計算差值接近，反演參數基本合理。泄洪閘位移云圖如圖2、3所示。

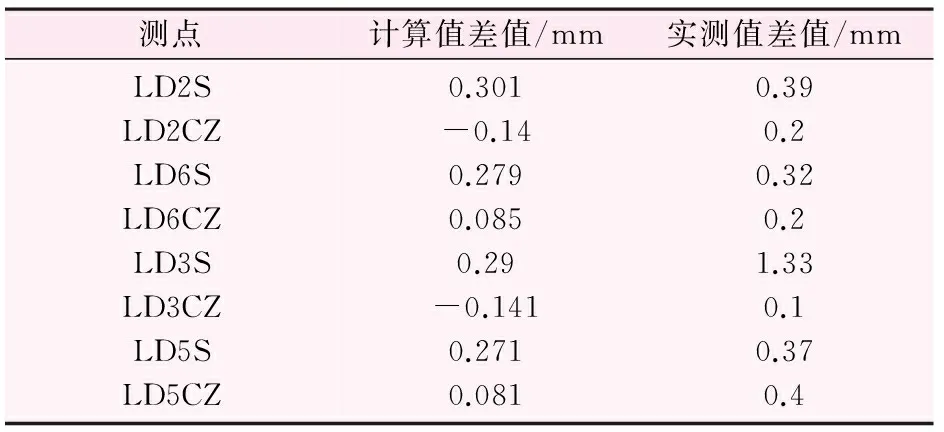
表2 計算值差值與實測值差值數據對比表

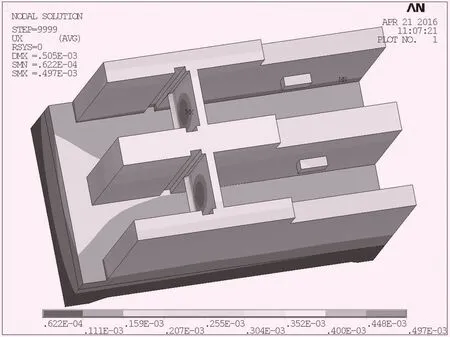
圖2 泄洪閘順河向位移云圖

5 典型工況下大壩變形及應力分析

5.1 判定標準

(1) 沉降：根據SL265-2001《水閘設計規范》規定，天然土質地基上水閘地基最大沉降量不宜超過15 cm，相鄰部位最大沉降不宜超過5 cm。

(2) 應力：依照GB50010-2002《混凝土結構設計規范》規定，混凝土的抗壓抗拉強度滿足混凝土強度設計值的要求，計算所用到混凝土強度設計值：C20，抗壓9.6 MPa、抗拉1.10 MPa；C40，抗壓19.1 MPa、抗拉1.71 MPa。

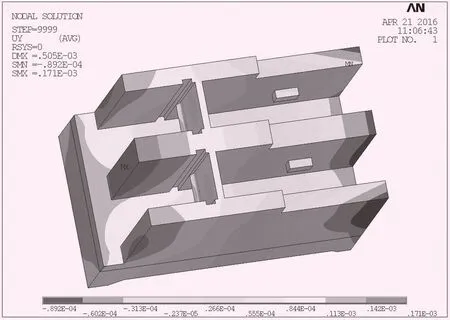
圖3 泄洪閘垂直位移云圖

5.2 選取的計算工況

(1) 正常蓄水位工況：上游1 090.00 m，下游無水。

(2) 設計洪水位工況：上游水位1 084.60 m，下游水位1 073.80 m。

(3) 校核洪水位工況：上游水位1 088.85 m，下游水位1 072.20 m。

利用反演出的參數，對泄洪沖沙閘及表孔閘在正常蓄水位工況、設計洪水位工況、校核洪水位工況3種工況下進行了安全性論證，結果表明：

(1) 3種工況下泄洪閘的位移值均較小，且對比可知正常蓄水位工況下泄洪閘的位移值最大，最大順河向位移產生于閘墩頂部，位移值為1.46 mm，最大豎向位移發生于閘墩下游頂部，位移值為-2.75 mm。表孔閘在對應工況下變形規律與泄洪閘類似，在正常蓄水位工況下表孔閘的位移值最大，最大順河向位移產生于閘墩頂部，位移值為0.75 mm，最大豎向位移發生于閘墩下游頂部，位移值為-2.6 mm。兩壩段在3種典型工況下變形均在規范允許范圍之內，是安全的。

(2) 3種工況下將大小主應力進行對比發現，泄洪閘在正常蓄水位工況下應力最大，最大壓應力為-1.63 MPa，出現在閘墩與閘底板相接處，最大拉應力為1.99 MPa，出現在牛腿與邊墩的接觸面上。表孔閘在校核工況下應力最大，最大壓應力為-1.4 MPa，出現在閘墩與閘底板相接處，最大拉應力為0.233 MPa，出現在溢流面處及閘室下游的末端位置。兩壩段在3種典型工況下應力均在規范允許范圍之內，是安全的。

綜上所述，反演參數基本合理且安全，反演方法正確可行。

6 結 語

本文通過分析研究多種反演分析方法，結合電站監測資料，采用非線性問題的位移正反分析方法。位移正反分析法基于正演分析，方法靈活，程序簡單，適用于電站大壩參數的反演。通過對某電站大壩泄洪沖沙閘及表孔閘進行了有限元模擬，采用基于多重響應面的位移正反分析法，對影響大壩位移的基巖t1彈模、基巖t2彈模、基巖t1泊松比、基巖t2泊松比、C10彈模、C20彈模進行了反演分析。結果表明：計算值與實測值中大部分值擬合的較接近，參數反演基本合理且參數反演方法正確可行。同時利用反演分析得到的參數通過對泄洪沖沙閘及表孔閘2個閘壩段在正常蓄水位、設計洪水位、校核洪水位3種工況下進行了變形及應力分析。位移分布符合實測規律，位移值及應力值在規范允許范圍內，參考類似工程，反演參數值合理[10]。

參考文獻:

[1] 周萍.基于神經網絡和遺傳算法的巖體參數反分析研究[D].南京：河海大學,2004.

[2] 吳瓊.隧道動態設計中圍巖計算參數的應力反分析研究[D].成都：西南交通大學,2006.

[3] 周麗君.時空效應下巖質邊坡位移反分析研究[D].重慶：重慶大學,2009.

[4] 徐韜.某巖質高邊坡穩定性計算與力學參數反分析[D].長沙：中南大學,2013.

[5] 裴建春.混凝土面板堆石壩原型觀測資料反饋分析研究[D].天津：天津大學,2007.

[6] 聞世強.茅坪溪瀝青混凝土心墻堆石壩反演分析[D].南京：河海大學,2004.

[7] 班宏泰,覃文文,趙昕,柏洪雪,謝鵬,費文平.巖體參數的反演分析方法[J].科技創新導報,2008(08):7-8.

[8] 唐光華.圍巖位移反分析及智能化灰色預測與模糊分類的應用[D].武漢：武漢理工大學,2005.

[9] 寧昕揚,劉曉青,牛志偉,齊慧君,潘世洋.基于響應面法的土石壩參數隨機反演分析[J].水電能源科學,2017(01):73-76.

[10] 雷曉鋒,馬雙科,鄭婭娜.某水電工程地下廠房開挖的巖體參數反分析[J].中國農村水利水電,2017(07):140-143.