步進電動機SPWM微步距細分控制的研究

趙 濤，季寧一，劉漢忠，沈維健

(1.南京工程學院，南京 211167；2.南瑞集團有限公司國網電科院有限公司，南京 210003)

0 引 言

步進電動機具有控制簡單、無積累誤差等優點[1]，在數控系統、伺服控制系統、機器人終端定位及計算機外圍設備等領域廣泛應用[2-3]。由于步進電動機低速時存在轉動振動、明顯的步進現象、轉速不夠平穩以及運行時易發生振蕩[5]等問題，限制了步進電動機在一些高性能、高精度場合的應用。為了解決上述問題，國內外學者進行了深入的研究，在控制系統、控制策略等方面提出了很多解決方案。目前應用最多的是采用微步距控制的細分驅動技術[4-6]。 其中的一種方案是以單片機通過專用集成芯片來控制其脈沖輸出頻率和脈沖輸出數，實現步進電動機的速度控制和位置定位[5-6]。隨著電子技術的發展，高性能的微處理器MCU及數字信號處理芯片DSP性能越來越好，價格也越來越便宜。相對于專用步進電動機微步控制芯片，采用MCU、DSP具有控制靈活，驅動功率范圍大等特點，同時也更方便實施較為復雜的控制策略，以獲得較好的控制效果[7]。因此，利用高性能MCU、DSP直接實現步進電動機微細分控制的應用受到廣泛的重視。

本文以二相混合式步進電動機為控制對象，在研究二相混合式步進電動機SPWM微步距細分控制原理的基礎上，對步進電動機細分驅動時的電磁轉矩進行深入的分析，對基于高性能MCU的SPWM細分控制系統進行了設計。

1 SPWM細分原理及電磁轉矩分析

1.1 SPWM微步距細分原理

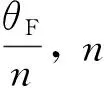
根據文獻[1]，二相混合式步進電動機的電磁轉矩方程可表示：

Te=-pψM[iAsin(pθ)+iBcos(pθ)]-Tdmsin(2pθ)

(1)

式中:選取轉子的N極對準A軸時為轉子參考位置，此時轉子角度θ=0°；Tdm為磁極之間的磁通對轉子影響產生的定位轉矩；ψM為磁鏈；p為磁極齒數，其可由式(2)表示：

(2)

式中：m為電機的相數。

如果忽略定位轉矩，步進電動機工作在整步驅動時，每個步距角θF對應90°電角度，則式(1)可以表示為：

Te=pψM(iAsinθE+iBcosθE)

(3)

式中:θE為轉子的電角度。

當步進電動機工作在SPWM細分時，對于二相步進電動機， 細分驅動時A,B相電流可以表示為：

(4)

1.2 SPWM細分驅動電磁轉矩分析

根據式(3)和式(4)可推出SPWM微步距細分驅動時(細分數n為任意值)的電磁轉矩表達式:

Te=pψMIsin(θE-θk)=TMsin(θE-θk)

(5)

由式(5)可得到細分數n為不同值時步進電動機電磁轉矩Te隨轉子電角度θE變化的曲線。圖1給出了基于Mathcad的細分數n在不同值時電機的電磁轉矩與最大電磁轉矩TM隨旋轉角度的變化曲線。

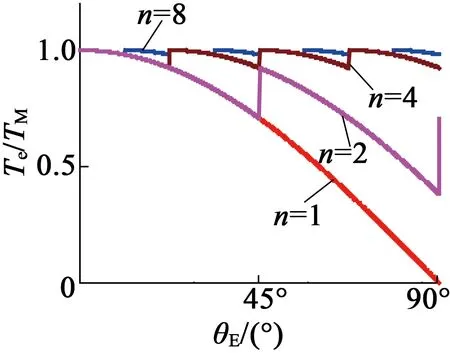
圖1 電磁轉矩變化曲線

對式(5)進行積分，可得到90°電角度范圍內電機總有效轉矩表達式：

(6)

為了進一步分析在不同細分數時轉矩變化的情況，根據文獻[8]的總有效轉矩方差：

(7)

根據式(6)、式(7)，給出了細分驅動和整步驅動總有效轉矩比及方差隨不同細分數變化的曲線，如圖2所示。

圖2 細分驅動時轉矩隨細分數變化規律

由圖1和圖2 可知， 在細分數較大時， 細分工作方式可使步進電動機的總有效轉矩顯著增加，步進電動機細分工作時比整步工作時轉矩的波動幅度也明顯減小，當n≥8時，電機的電磁轉矩近似恒定，步進電動機總有效電磁轉矩的方差接近于 0；此外， 隨著細分數的增加，電磁轉矩波動的幅度減小，波動的頻率增加，細分控制可以有效地改善步進電動機的性能，但還有其它如齒槽、鐵心等因素及結構和安裝等問題都會對電機性能產生重要的影響。此外，當細分數較大時再提高細分數，對電機性能提升效果也不顯著，同時在高速高細分的情況下器件的開關頻率高，開關器件損耗也變大。

2 SPWM細分控制系統設計

2.1 系統結構

圖3給出了步進電動機SPWM細分控制系統框圖。直流電源經過2個全橋PWM變換器分別控制電機的二相繞組，控制系統接收給定的控制信號，根據SPWM細分微步距控制器產生對應的SPWM信號，從而控制全橋PWM變換器達到控制電機的目的。全橋PWM變換器采取雙極性和單極性控制方式，通過對電機繞組電流進行快衰減、慢衰減及混合衰減的控制，可以使步進電動機定子繞組電流正弦度更好[2,5]。

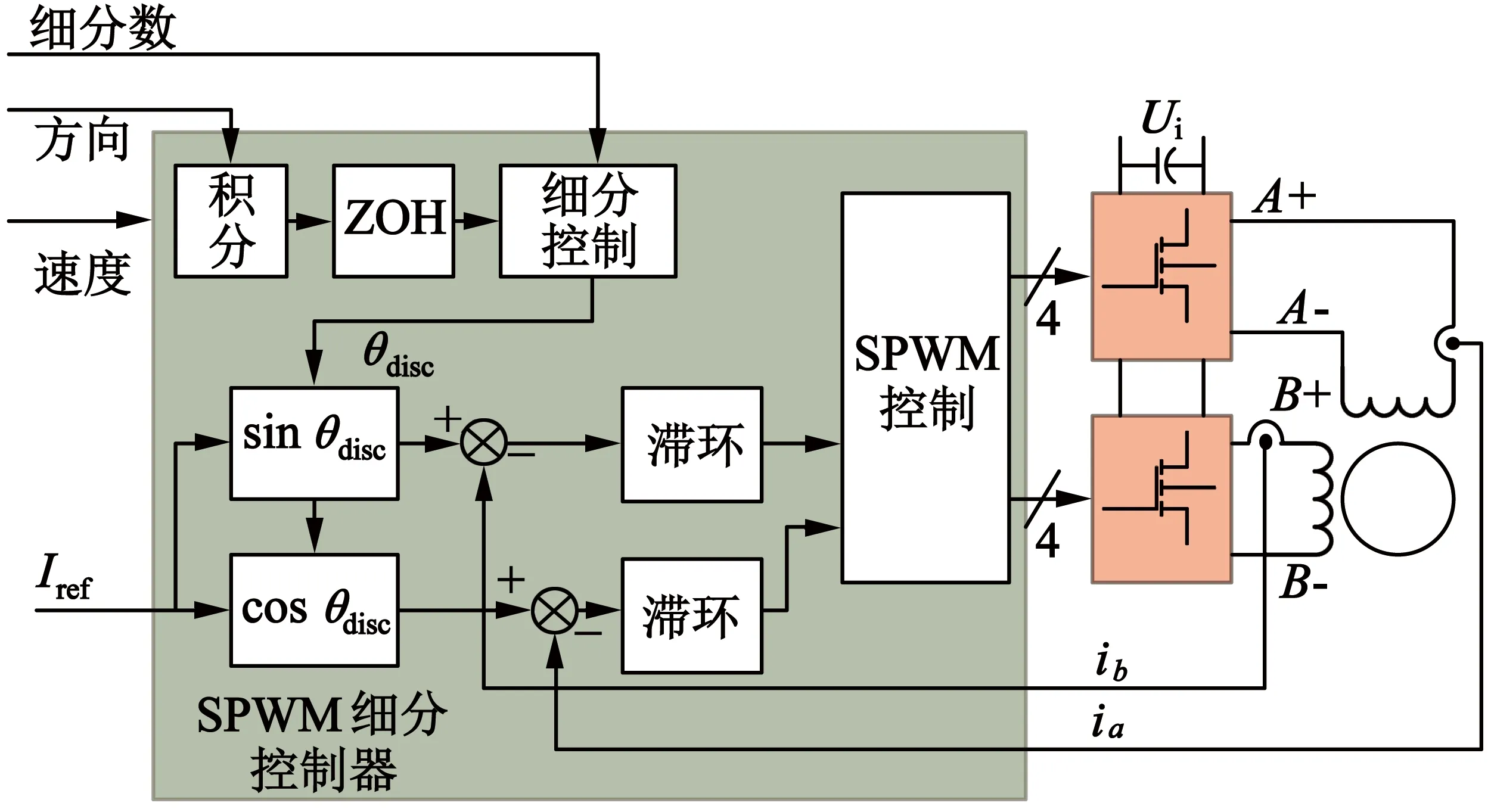
圖3 步進電動機SPWM控制系統框圖

2.2 SPWM細分控制策略

步進電動機每相繞組通過SPWM 脈沖， 進行正弦脈寬調制，可以對步進電動機步距角進行任意的細分。二相混合式步進電動機SPWM細分驅動的關鍵就是控制電機二相繞組的電流，使其為正弦規律的階梯波，階梯數越多則細分數越高，頻率越大則電機轉速越高。

首先根據最大細分數N確定對應的正弦、余弦表，根據方向設定細分數n，由式(8)可以得到下一步的指針P(k+1) ：

(8)

式中：N為n的2的倍數，P(k+1)不大于N，根據指針查表得出對應的sinθk+1和cosθk+1值。

式(4)在這里可以變換:

(9)

根據式(9)可以得到下一步細分所需要的A,B兩相電流值。該值和電機電流，經過滯環比較控制，輸入到SPWM發生器，輸出SPWM控制脈沖。根據速度指令設置定時器的時間常數，控制每個階梯波的作用時間，即可控制正弦階梯數的頻率，從而控制電機的轉速。

3 仿真與實驗研究

按照圖3給出的結構框圖，基于MATLAB/Simlink建立了步進電動機微步距控制的仿真模型，并采用32位單片機STM32F103設計了步進電動機SPWM細分驅動系統。本文的仿真建模及實驗波形是以二相混合式步進電動機57H56605為對象，表1給出了步進電動機的主要參數。

表1 步進電動機參數

在細分數變化的情況下步進電動機A,B相的電流波形和電機旋轉角度的仿真波形如圖4所示。圖4中電機轉速為1 000 步/秒，先以n=4微步距運行，0.1 s后以n=16微步距運行。如果要保證電機轉速不變，細分數增加，則換步的時間變小。當細分數較小時步進電動機存在步進現象，步距角較大，低速轉動時產生振動，轉速不夠平穩；細分數n=16時，A,B相電流波形正弦度較好，轉子位置波形平滑，實現微步轉動。在細分數變化過程中，電機繞組電流變化也比較平滑。

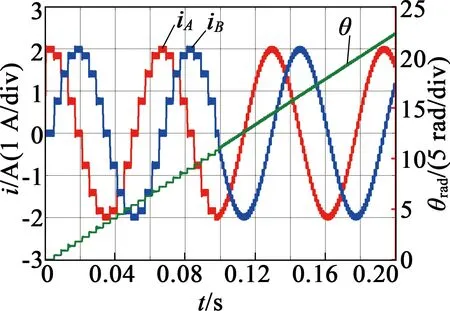
圖4 不同細分時的仿真波形

圖5給出了細分數n=16時，電機正轉變為反轉時的電流和旋轉角度的仿真波形。電機一開始正轉，0.1 s后方向控制信號由1變為-1，電機反轉；反轉時B相電流由滯后A相電流90°變為超前A相電流90°。在正反轉切換過程中，電流變化平穩，電機轉速沒有出現過沖；在0.2 s電機轉角回原位。

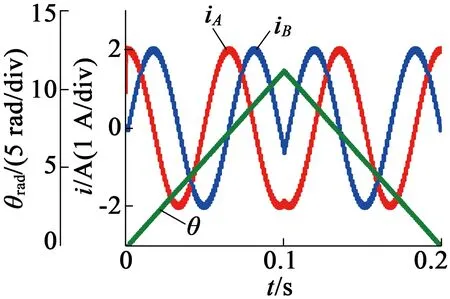
圖5 正、反轉運行時的仿真波形

圖6給出了在不同細分數下，步進電動機定子繞組電流的實驗波形，電流波形通過電流探頭獲取。從圖6中可以看出，步進電動機工作在8細分時， 電流波形已經趨近正弦波，但還存在較明顯的臺階，電流正弦度不夠好，其合成磁場是多邊形，電機運行還存在步進現象。隨著細分數增加，A,B相電流也越接近正弦波；在步進電動機細分數n=128時，定子繞組電流波形正弦度好，A,B相電流的相位也保持穩定，說明系統對電流的控制效果較好。電機繞組受到正弦與余弦電流的激勵，磁場圓形度好，電機運行平穩。在電機起動時，可以讓電機以高細分數運行，再按照梯形、S形加速，逐漸減少細分數，這樣在相同的換步時間下，細分數少，電機轉速高。

(a) 細分數n=8

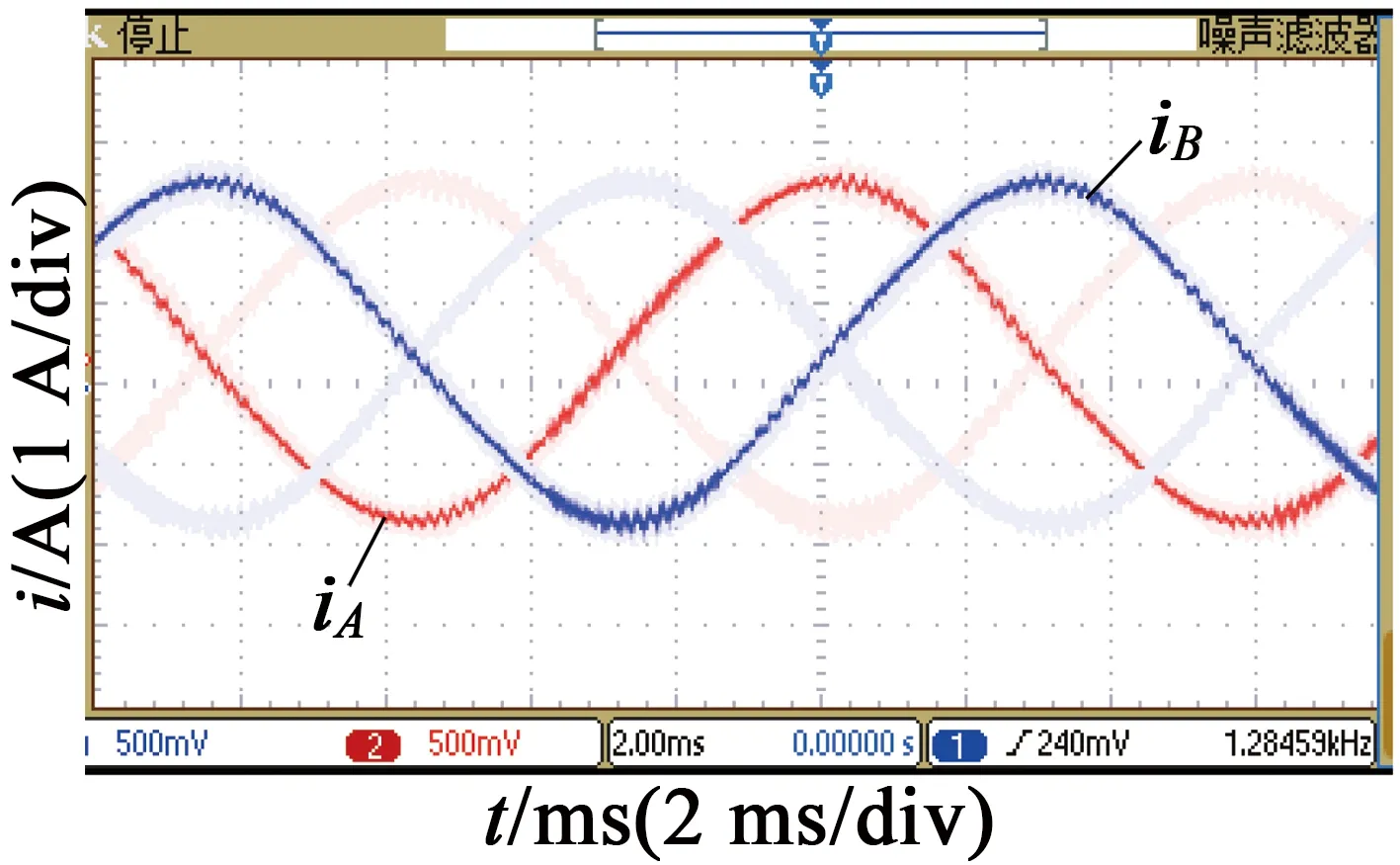
(b) 細分數n=16

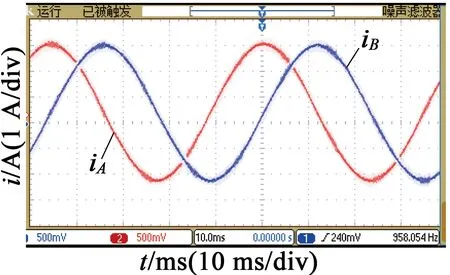
(c) 細分數n=128

SPWM細分控制可使電流變化趨緩，通過對電流的控制達到對電機運行狀態的控制，使得電機運行時噪聲降低，同時由于步距角降低，在高細分數時電機的扭矩也得到增強，帶負載能力得到了提升。此外，該系統的硬件結構簡單，開展功能多，成本較低，細分精度高，可以靈活控制步進電動機的細分數。

4 結 語

本文對SPWM細分微步距驅動時步進電動機的電磁轉矩進行了分析，從理論上闡述了采用SPWM細分可使步進電動機有效電磁轉矩增加、電磁轉矩波動幅度減小，采用SPWM細分能夠有效地克服步進電動機低頻振蕩、高頻失步等缺點，提高步進電動機的運行性能。在此基礎上，對基于MCU的步進電動機SPWM細分微步距控制系統進行了研究和實現。仿真和實驗表明，該系統細分的切換容易，步進電動機定子繞組流正弦度好，改善了步進電動機的步進現象，達到了微步距轉動、運轉平穩的目的。

[1] ACARNLEY P.Stepping motors-a guide to theory and practice,4th edition[M].LondonL:The Institution of ElectricalEngineers,2002.

[2] 鄭雪欽，郭東輝.基于混合模式PWM二相步進電機驅動控制的研究[J].系統仿真學報，2012，24(2):456-461.

[3] 趙濤.基于CAN總線太陽能電池自動跟蹤控制器的設計[J].制造業自動化，2012(12):105-108.

[4] 楊 斐， 劉景林， 董亮輝.兩相混合式步進電動機動態多細分驅動器設計[J].微特電機，2013，41(2):42-44,47.

[5] GAAN D R,KUMAR M,SUDHAKAR S.Frequency modulation based microstepping of stepper motor for real time position tracking applications[C]//IEEE International Conference on Power Electronics,Drives and Energy Systems.IEEE,2017:1- 6.

[6] 田云， 張宏龍.基于SA4828的三相步進電動機細分驅動[J].微特電機，2013，41(7):63-66.

[7] 顧鳳香, 黃云龍, 陳國定.基于TMS320F2812的步進電動機任意可變細分控制系統研究[J].微電機，2009,42(5):28-30.

[8] 李茂軍， 劉鼎邦.步進電機細分驅動電磁轉矩分析[J].控制工程，2013,20(2):243-245.